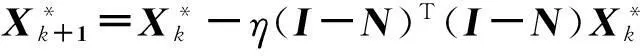基于高频和中频信息的图像超分辨率重建
2016-01-22陈伟超陈华华
陈伟超,陈华华
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
摘要:提出一种基于图像高频和中频信息的超分辨率算法。分别将图像高频和中频作为高分辨图像和低分辨率图像的特征,以图像高频和中频信息作为训练样本对,采用全局迭代收缩方法(GISA)进行稀疏分解,获得高、中分辨率字典对。根据测试图像对应的中频信息和字典对获得图像高频信息,结合测试图像插值放大结果,经非局部相似性方法处理后获得高分辨率图像。实验结果表明,提出的方法具有较高的重建质量。
关键词:高频;中频;字典;超分辨率
DOI: 10.13954/j.cnki.hdu.2015.01.010
基于高频和中频信息的图像超分辨率重建
陈伟超,陈华华
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
摘要:提出一种基于图像高频和中频信息的超分辨率算法。分别将图像高频和中频作为高分辨图像和低分辨率图像的特征,以图像高频和中频信息作为训练样本对,采用全局迭代收缩方法(GISA)进行稀疏分解,获得高、中分辨率字典对。根据测试图像对应的中频信息和字典对获得图像高频信息,结合测试图像插值放大结果,经非局部相似性方法处理后获得高分辨率图像。实验结果表明,提出的方法具有较高的重建质量。
关键词:高频;中频;字典;超分辨率
DOI:10.13954/j.cnki.hdu.2015.01.010
收稿日期:2014-04-24
基金项目:浙江省自然科学基金资助项目(Y1111213)
通信作者:
作者简介:陈伟超(1989-),女,浙江缙云县人,在读研究生,数字图像处理.陈华华副教授,E-mail: iseealv@hdu.edu.cn.
中图分类号:TP391
文献标识码::A
文章编号::1001-9146(2015)01-0049-04
Abstract:An image super-resolution(SR) reconstruction algorithm based on high- and mid-frequency components is proposed in this paper. The algorithm selects high- and mid-frequency of natural images as the feature of high-resolution(HR) images and low-resolution(LR) images respectively. Patch pairs, composed of high- and mid-frequency components, are trained by GISA(generalized iterated shrinkage algorithm) to obtain the high-resolution and mid-resolution joint dictionary pair. According to the mid-frequency of the test image and the dictionary pair, image high-frequency is reconstructed. Then, combined with interpolated LR images and reconstructed high-frequency, the HR image is reconstructed after a non-local similarity regularization term. Experimental results show that the proposed method has better performance.
0引言
图像由于模糊、下采样和噪声等因素,形成了低分辨图像。超分辨率重建是指从输入的低分辨率图像中恢复高频信息,获得高分辨率图像的过程。插值方法是超分辨重建的一种常见方法,但插值图像边缘有锯齿效应。迭代反向投影方法(Iterative Back-Projection, IBP)[1]也是一种经典超分辨率方法,但重建图像细节并不丰富。正则化超分辨率重建的经典方法是全变分(Total Variation, TV)[2],该方法能有效地抑制噪声,但在一些细节上会出现过平滑现象,产生一些模糊。近年来,受到压缩感知的启示,信号的稀疏特性可以减少信号处理复杂度。文献[3]将稀疏表示理论应用于图像处理反问题中,主要研究稀疏分解复杂度的降低问题。图像可以被字典展开成一个稀疏表达式,经典的方法是文献[4]的基于稀疏表示的图像超分辨率方法,但是该算法的重建图像在边缘细节上不够平滑。本文提出一种基于图像高频和中频信息的超分辨率算法。实验结果表明,本算法具有较高的重建质量,重建图像的边缘结构锐化效果较好。
1基于高频和中频信息的图像超分辨率重建
1.1 图像高频和中频信息提取
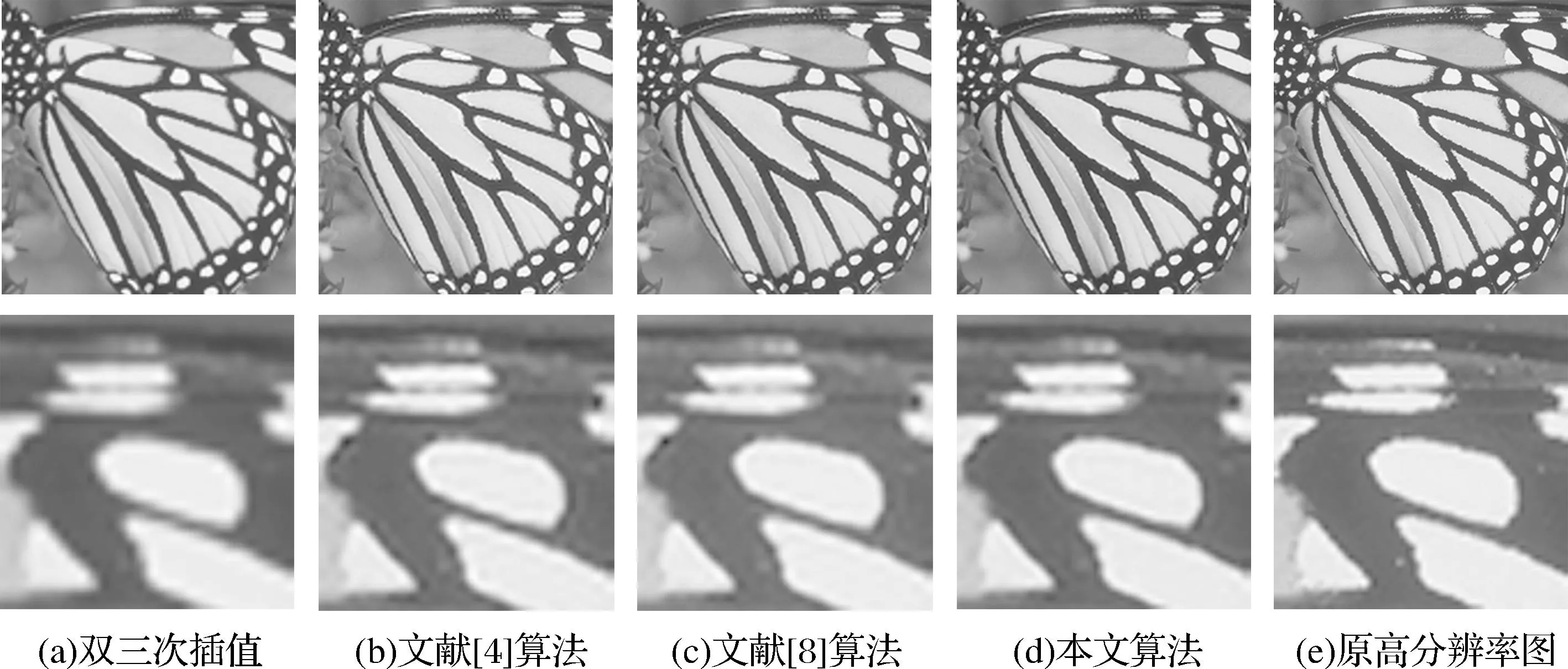
不同频率信息在图像结构中有不同的作用。图像的主要成分是低频信息,它形成了图像的基本灰度等级,对图像结构的决定作用较小;中频信息决定了图像的基本结构,形成了图像的主要边缘结构;高频信息形成了图像的边缘和细节,是在中频信息上对图像内容的进一步强化[5]。因此,人眼对图像的中高频信息比较敏感,若中高频信息发生变化,那人眼能够提取的图像信息就有局限性。因而,本文将图像的高频信息Xh和中频信息Xm作为样本对进行训练,获得对应的高、中频字典Dh、Dm。原始高分辨率图像X与低分辨率图像Y经插值放大后的图像的差值为高频信息,即Xh=X-Xb;插值放大后的图像与插值放大并经低通滤波器处理后图像之间的差值为中频信息,即Xm=Xb-φXb;插值放大图像经低通滤波器处理后的图像φXb为低频信息。低通滤波器φ为7×7的高斯低通滤波器,其方差为1.6。本文超分辨率重建方法基于测试图像的中频信息,恢复出其丢失的高频信息。图像的高频和中频如图1所示。图1中,第一行为测试图像丢失的高频信息,第二行为根据测试图像提取的中频信息。

图1 图像的高频和中频
1.2 字典对训练
假设D∈Rn×Q是维数为n、原子数为Q的过完备字典,x∈Rn表示图像子块,则图像的稀疏表示为:
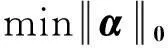
(1)
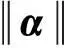
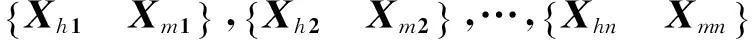
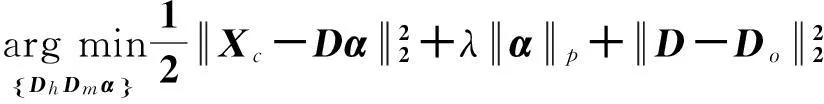
(2)
采用分步迭代法分别求解D和α,算法步骤如下:
1)初始化。循环次数k=0,最大循环次数max=40,D为单位化的高斯随机矩阵;
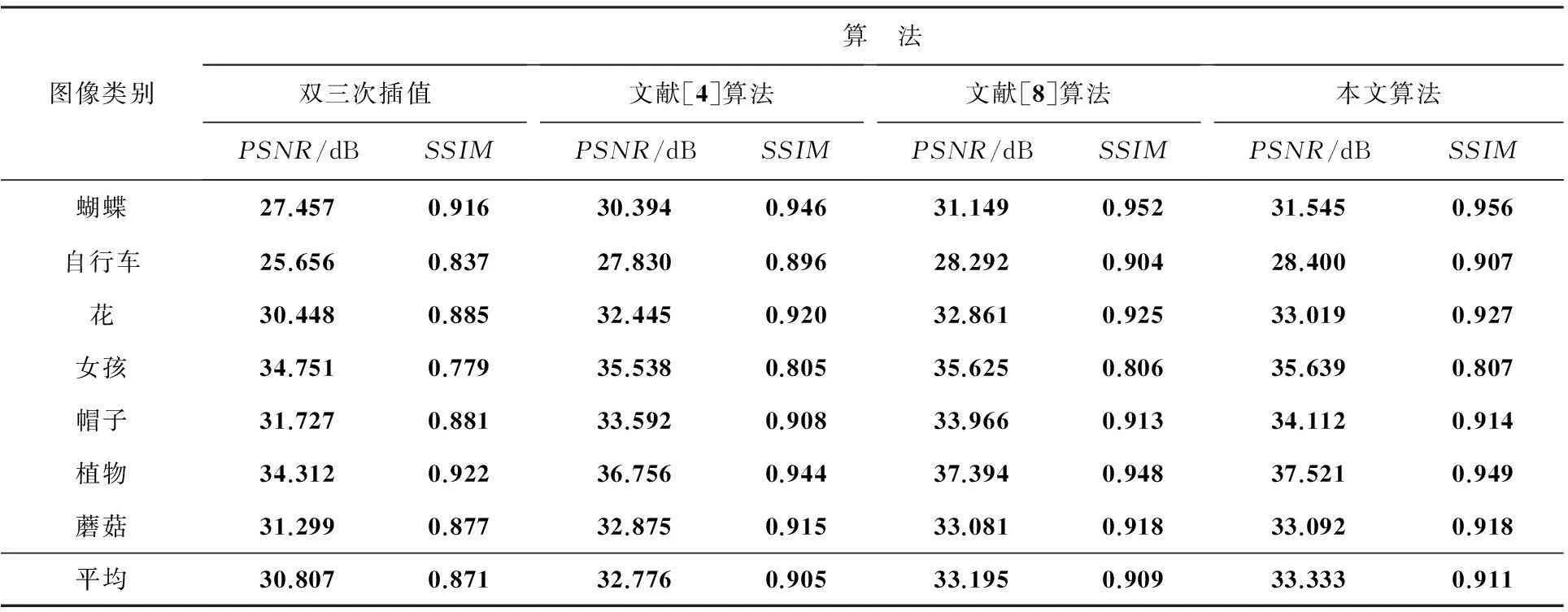
2)当k (1)固定D,求解稀疏表示系数α; (3) 即α=GISA(Xc,D,λ,p)。 (2)固定α,求解字典对D; (4) 即DT=(ααT+I)-1(XcαT+Do)T。 (3)k=k+1,结束循环,输出Dh、Dm。 本文图像重建方法基于两个字典,中频字典Dm用于测试图像中频信息的稀疏分解,高频字典Dh用于高频信息的重建。先根据待重建的低分辨率图像Y获得插值放大后图像Xb并提取中频信息Xm;根据中频信息Xm和中频字典Dm,用GISA方法进行稀疏分解,即α=GISA(Xm,Dm,λ,p);高频信息Xh=Dhα结合插值放大后的图像Xb,初步重建出高分辨率图像X*。由于自然图像有很多相似结构,即有大量冗余信息,因此本文利用图像冗余信息对X*进行优化。非局部相似性的基本思想是将X*分成图像块,在图X*中寻找与当前图像块匹配的块,然后对这些块进行加权处理[7]。本文对X*用梯度下降法进行非局部相似性约束。用梯度下降法对X*进行非局部相似性约束: (5) 式中,η为约束系数,I为单位矩阵,N为非局部相似性矩阵[7],k表示第k次迭代。最后采用反向投影法[1],重建出高分辨率图像X*。 2实验结果 训练图像采用文献[4]的68张自然图像,先对每张图像进行高频、中频信息提取,再分别得到100 000个6×6的高频图像块{xh}和中频图像块{xm}。训练字典时,λ为0.08,p为0.7。训练得到的高、中频字典原子数为512。重建时,对低分辨率图像进行2倍放大,重叠像素为5,非局部相似性约束系数η为0.05。由于人眼对于亮度分量y更为敏感,本文对y进行超分辨重建,对蓝色色度分量cb和红色色度分量cr分量直接用双三次插值放大。 本文的测试图像如图2所示,图2为7张低分辨率图像,并与双三次插值、文献[4]方法、文献[8]方法进行了对比。表1为7张低分辨率图像的重建结果,从表1中可知本文方法比其他3种方法具有更高的峰值信噪比(PSNR)和结构相似度(SSIM)。本文方法平均PSNR比文献[4]方法高0.557 dB,比文献[8]方法高0.138 dB。蝴蝶的重建结果图及其放大细节如图3所示,从图3可知,本文方法具有精细的边缘结构,且在细节上锐化效果较好。本文方法主要根据中频信息复原高频信息,由图1可知,高中频信息主要表现为图像的边缘结构和细节,因此本文方法能较好地表示图像边缘。由于女孩、蘑菇图纹理复杂且提取的中频信息较少,因此相对其他图像来说,其PSNR和SSIM相对提高的较少。 图2 低分辨率图像表 表1 基于高频和中频信息的超分辨率重建结果 图3 蝴蝶图重建结果及其1.3倍放大细节图 3结束语 本文提出了一种基于高频信息和中频信息的图像超分辨率重建算法。本算法将图像高频和中频信息子块作为训练样本对,用GISA方法进行稀疏分解,训练得到高、中频字典对。根据测试样本对应的中频信息和字典对获得图像高频信息,结合测试图像插值放大结果,经非局部相似性处理后获得高分辨率图像。实验结果表明,本文方法具有较高的重建质量,重建图像的边缘结构锐化效果较好。 参考文献 [1]Irani M, Peleg S. Motion analysis for image enhancement: Resolution, occlusion, and transparency[J]. Journal of Visual Communication and Image Representation,1993,4(4):324-335. [2]Marquina A, Osher S J. Image Super-Resolution by TV-Regularization and Bregman Iteration[J].Journal of Scientific Computing,2008,37(3):367-382. [3]孙玉宝,韦志辉,肖亮,等.基于稀疏表示的图像超分辨率重建快速算法[J].系统工程与电子技术,2010,32(12):2 696-2 700. [4]Yang J, Wright J, Huang T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing,2010,11(19):2 861-2 873. [5]叶盛楠,苏开娜,肖创柏,等.基于结构信息提取的图像质量评价[J].电子学报,2008,36(5):856-861. [6]Zuo W, Meng D, Zhang L, et al. A generalized iterated shrinkage algorithm for non-convex sparse coding[C]//Proceedings of the IEEE International Conference on Computer Vision (ICCV).2013:217-224. [7]Dong W, Zhang D, Shi G, et al. Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization[J]. IEEE Transactions on Image Processing,2011,20(7):1 838-1 857. [8]He L, Qi H, Zaretzki R. Beta process joint dictionary learning for coupled feature spaces with application to single image super-resolution[C]//IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2013:345-352. Image Super-resolution Reconstruction Based on High-and Mid-frequency Components Chen Weichao, Chen Huahua (SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China) Key words: high-frequency; mid-frequency; dictionary; super-resolution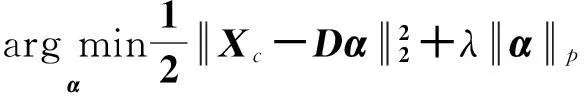

1.3 图像重建