钢轨焊缝不平顺对扣件弹条动应力的影响分析
2016-01-21刘小军赵春发
刘小军 赵春发 张 徐
(西南交通大学牵引动力国家重点实验室 四川成都 610031)
钢轨焊缝不平顺对扣件弹条动应力的影响分析
刘小军赵春发张徐
(西南交通大学牵引动力国家重点实验室四川成都610031)
摘要:建立弹条Ⅱ型扣件有限元模型,开展了不同波深、不同波长焊缝不平顺条件下弹条动应力分析。研究结果表明:扣件安装到位后其力学性能指标符合铺设安装规范要求,弹条后弯肢内侧表层出现轻微局部塑性屈服,建立的扣件有限元模型能较准确模拟弹条应力状态;有焊缝不平顺时弹条动应力幅值较平顺线路显著增大,会加快弹条疲劳伤损;弹条动应力幅值和轮对通过瞬间突变应力幅值均随焊缝不平顺波深增大而线性增大,随不平顺波长减小先缓慢增加,波长小于0.2 m以后急剧增大。
关键词:弹条扣件动应力轨道不平顺非线性接触有限元法
扣件是轨道结构重要组成部分,其作用是固定钢轨位置,阻止钢轨纵、横向移动,防止钢轨倾覆,为轨道提供必要的弹性。扣件荷载条件恶劣,服役过程中会出现松动、脱落、疲劳断裂等失效现象,从而加快轨道结构部件伤损[1]。近年来我国重载列车轴重加大,行车速度提高,加剧了轮轨动力作用,导致轨道结构部件伤损率增大,对铁路货运安全性和经济性造成不利影响。其中,焊接区钢轨及扣件弹条疲劳伤损问题尤为突出,有必要对焊缝不平顺激扰下弹条动应力及疲劳伤损进行分析,为轨道结构加固和运营维护提供参考。
国内外学者开展了扣件性能测试分析、弹条安装受力与变形分析以及弹条动应力与疲劳可靠性研究等[1-6],但对焊缝区弹条进行动应力分析的研究工作尚未见报道。本文针对我国重载铁路大量使用的弹条Ⅱ型扣件,建立考虑部件非线性面面接触和弹条材料塑性屈服的扣件有限元模型,通过扣件安装受力分析和车辆-轨道耦合动力学分析得到扣件预压荷载和服役动荷载,比较分析不同波长、不同波深钢轨焊缝不平顺激扰下弹条的动应力响应,获得钢轨焊缝不平顺对弹条动应力的影响规律。
1扣件有限元模型
图1为弹条Ⅱ型扣件装配图,其安装过程是通过拧紧螺栓压缩弹条,使弹条发生变形而产生扣压力,将弹条前肢扣压在轨距挡板和钢轨上方。服役过程中钢轨与轨枕相对位置可能发生变化,扣压力也随之变化,因此,弹条必需提供足够的初始扣压力,用以确保钢轨与轨枕可靠联接。
扣件安装与服役期间,弹条表面允许有局部塑性变形,各部件之间存在微小滑动,这些都会影响扣件力学性能和弹条应力应变状态,简化的扣件模型难以准确地模拟弹条受力与变形。本文按照《弹条II型扣件》(TB/T 3065.1-2002)规范[7],建立了包括弹条、平垫圈、轨距挡板和挡板座等部件的扣件有限元模型,如图2所示。
建模时不考虑螺旋道钉和螺母,建立平垫圈模型,约束其横向和纵向运动,通过对平垫圈施加竖向位移模拟螺栓对弹条的初始预压。模型中弹条与平垫圈、轨距挡板之间以及轨距挡板与挡板座之间建立面面非线性接触关系,采用库仑摩擦模型模拟两个弹性体接触界面之间的摩擦与相对滑动。为了提高模型计算效率,未建立钢轨实体模型,不考虑钢轨与轨距挡板接触问题,将轨下胶垫简化为与轨距挡板直接连接的弹簧,以便获取扣件扣压力。

图1 弹条Ⅱ型扣件装配图

图2 弹条II型扣件有限元模型
表1列出了弹条II型扣件模型主要材料参数。弹条采用60Si2CrVA优质弹簧钢,其抗拉强度为1 863 MPa,屈服强度为1 667 MPa。扣件安装过程中弹条后弯肢受到拉压、弯曲、扭转和剪切等复合作用,且允许发生局部屈服现象,因此,弹条采用了双线性随动强化本构模型和Mises材料屈服准则。

表1 弹条扣件有限元模型参数
2安装受力分析
按相关规范,弹条II型扣件安装到位是以弹条中部前端下颏与轨距挡板接触为准,或者使螺母扭力矩保持在100~140 N·m,安装到位后初始扣压力不大于10 kN,弹条中部前端行程不小于10 mm。对扣件进行有限元分析时,一般以弹条中部前端与轨距挡板接触作为安装到位的判断依据。采用图2扣件有限元模型,对平垫圈施加逐步增大的预压力来模拟弹条预压过程,获取扣件安装到位后的初始扣压力和弹条预压缩量,并为下节弹条动应力分析提供初始预压荷载。
图3是安装过程中扣压力、弹条中部前端位移、平垫圈位移随螺栓预压力变化曲线。可见,当螺栓预压力达到25 kN时,扣压力、弹条中部前端位移和平垫圈位移均出现拐点,说明弹条中部前端下颏与轨距挡板已发生接触,此时弹条安装到位,扣压力达到10.2 kN,弹条位移为10.7 mm,基本满足其铺设安装要求。当螺栓预压力进一步增大时,弹条和平垫圈位移基本不变,这是因为安装到位后扣件系统已作为一个整体“刚性结构层”提供扣压力,弹条也失去了本应该提供一定弹性的功能。
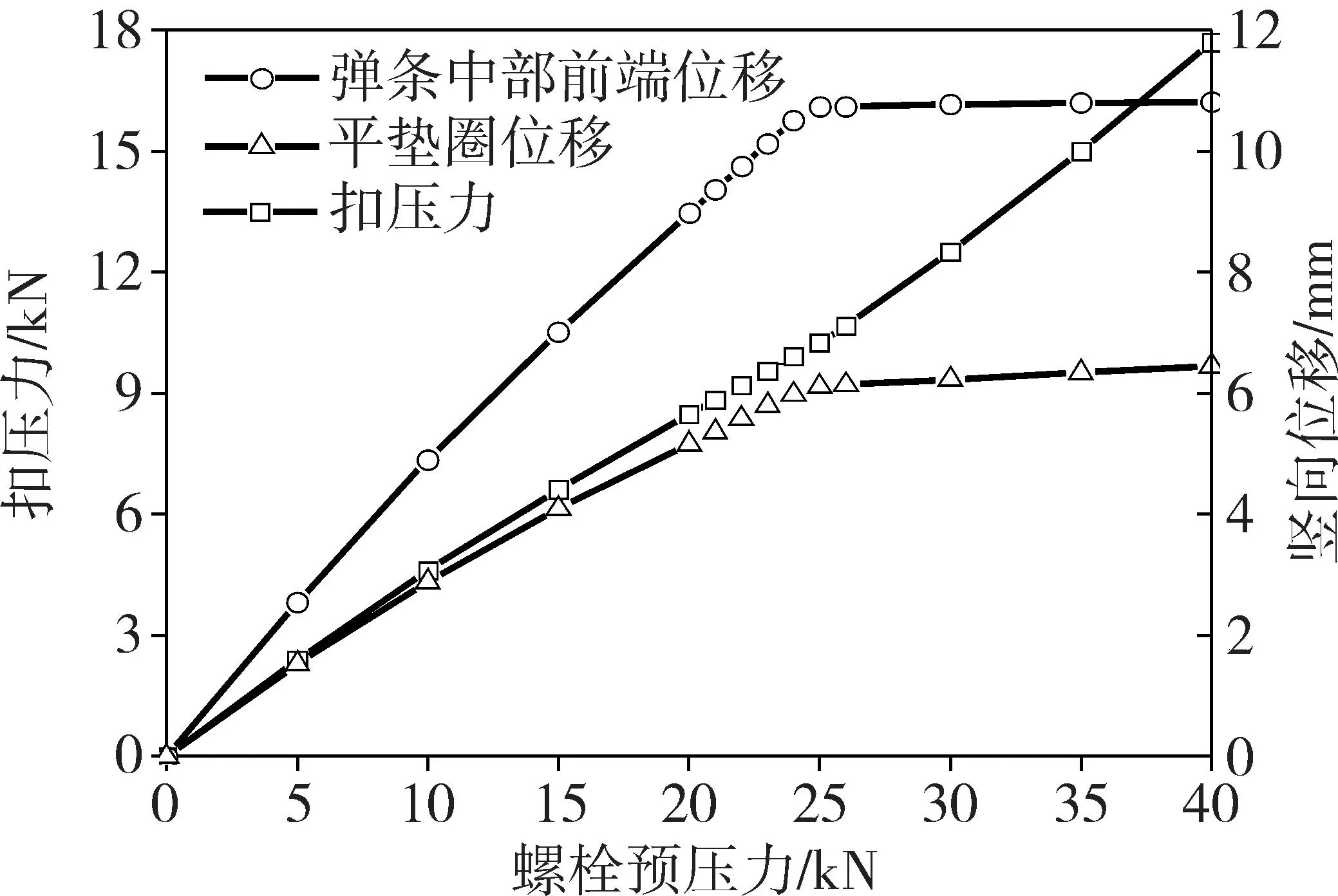
图3 扣压力和弹条位移随螺栓预压力的变化
图4是安装到位时扣件的等效应力云图。可以发现最大等效应力出现在弹条后弯肢内侧,与工程实际中弹条疲劳断裂多发生在此处相吻合。后弯肢内侧局部出现等效应力超过材料屈服极限的现象,即发生了局部塑性变形。
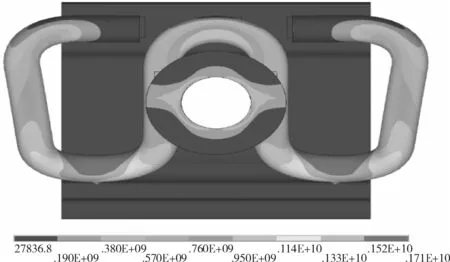
图4 扣件安装到位时等效应力云图
将弹条在最大等效应力处沿径向剖开,得到弹条横剖面应力云图。图5显示横剖面上弹条等效应力沿径向逐渐增大,且内侧表面应力大于外侧。进一步读取横剖面内A-A直径线路上的弹条等效应力值,得到等效应力沿径向分布曲线。图6表明弹条最大等效应力小于材料抗拉强度,表面局部塑性屈服的最大深度约为0.4 mm,该现象在工程实际中是可能且允许发生的[8]。

图5 弹条最大等效应力处横剖面应力云图
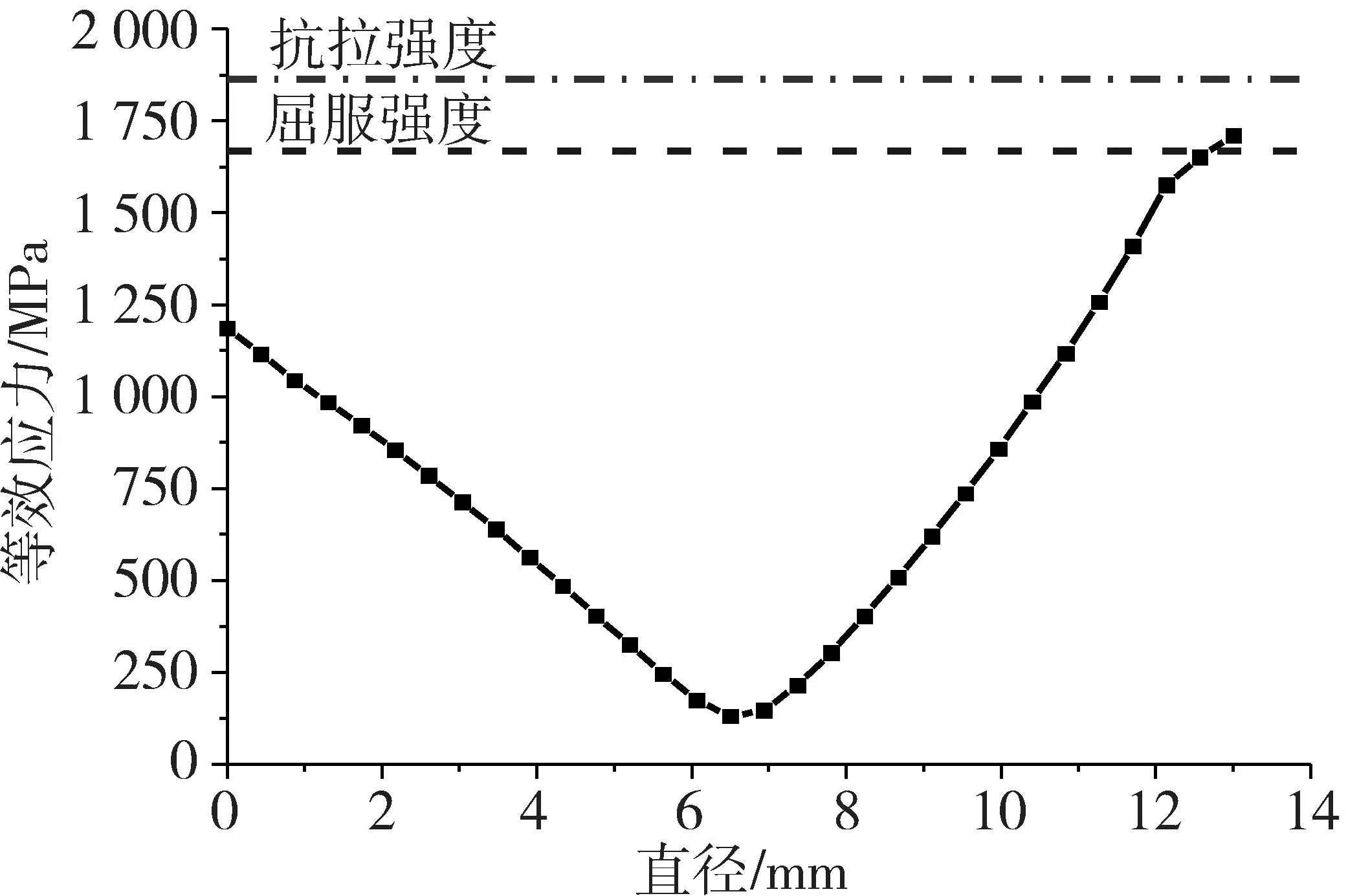
图6 A-A直径线上弹条等效应力分布
3弹条扣件动荷载模拟
采用车辆-轨道耦合动力学理论及其仿真计算方法[9],以我国30 t轴重货车和CHN75钢轨为对象,建立货车-轨道垂向动力学模型,计算得到焊缝不平顺激扰下车辆与轨道结构动力响应。然后,将获得的钢轨与轨枕相对位移作为扣件有限元模型的外部输入荷载,计算分析弹条动应力响应。
计算扣件动荷载时,车辆行车速度设定为80 km/h,焊缝不平顺采用1 m波长余弦波叠加短波的叠合型不平顺模型(图7)。根据朔黄铁路实测焊缝不平顺统计结果,短波波长范围为0.1~0.4 m,波深范围0.3~0.9 mm,波长1 m余弦波波深为0.3 mm。
图8是车辆以80 km/h速度通过焊缝不平顺(短波波长0.2 m,波深0.5 mm)和理想平顺线路时钢轨与轨枕相对振动位移曲线。需要说明的是,前后转向架通过时的位移曲线基本相同,故图中仅给出了前转向架通过时的响应曲线。由图8可见,平顺线路上钢轨与轨枕相对位移曲线平滑,位移最大值约0.37 mm;轮对通过焊缝不平顺线路时,轨道受到明显的冲击作用,相对位移幅值增大到0.49 mm,较平顺线路上增大约32%。
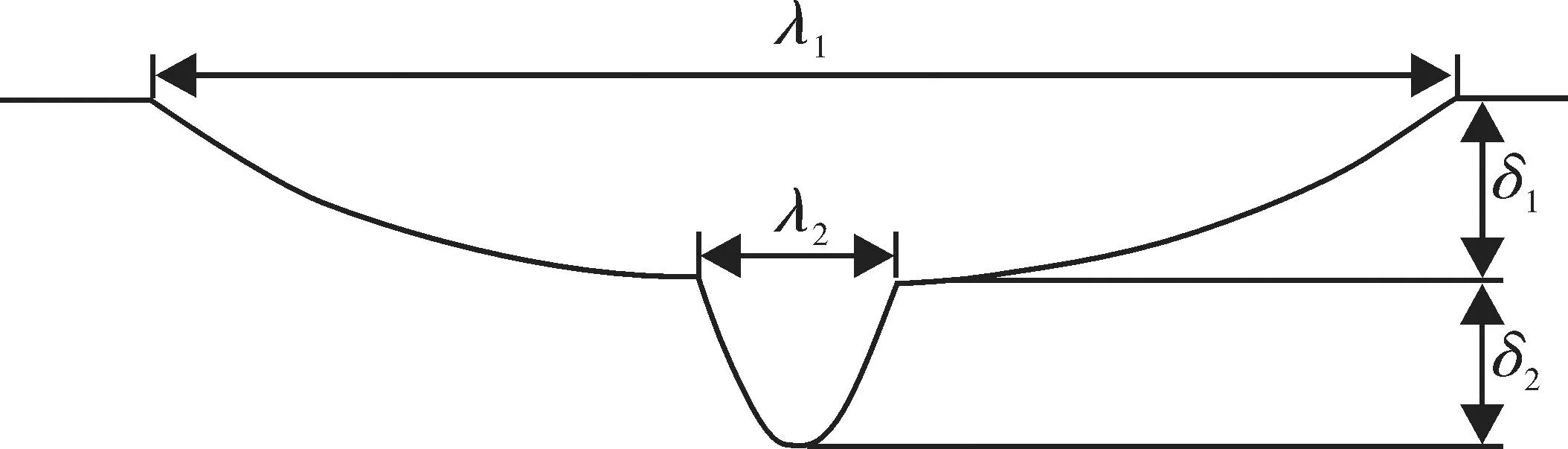
图7 叠合型钢轨焊缝不平顺模型

图8 钢轨与轨枕相对振动位移曲线
4弹条动应力分析
图9给出了焊缝不平顺短波波长为0.2 m、波深为0.5 mm时弹条的动应力响应,并与平顺线路上弹条动应力响应进行了对比。图9显示车辆通过时弹条等效应力小于扣件安装到位时的应力值,这是因为车辆荷载作用下胶垫受到压缩,钢轨相对轨枕向下移动,弹条等效应力峰值也随之降低。焊缝不平顺线路上弹条动应力幅值达110.4 MPa,较平顺线路上增加约30%;轮对通过焊缝瞬间弹条突变应力全幅值达到45.1 MPa,约为动应力幅值的41%。图9还表明轮对通过焊缝不平顺时弹条应力震荡剧烈,含有显著高频振动,这将加速弹条疲劳损伤。

图9 车辆动荷载通过时弹条等效应力
将焊缝不平顺短波波长设定为0.2 m,图10给出了弹条动应力幅值和突变应力幅值随短波波深的变化曲线。可以发现弹条动应力幅值和突变应力幅值基本上均随短波波深增大而线性增大,且后者增长速率明显大于前者。表2列出了波深为0.3,0.5,0.7和0.9 mm时弹条的动应力幅值。由表2可知弹条动应力幅值大致在100~130 MPa之间变化,突变应力幅值范围为30~80 MPa;当波深为0.9 mm时弹条突变应力幅值达82.2 MPa,约为波深为0.3 mm时的3倍。

图10 弹条动应力幅值与短波波深的关系

波深/mm动应力幅值/MPa突变应力幅值/MPa0.398.327.70.5110.445.10.7120.863.20.9129.282.2
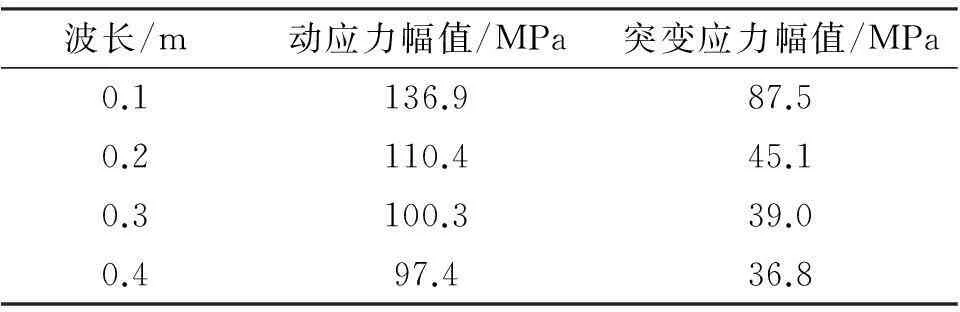
将焊缝不平顺短波波深固定为0.5 mm,计算了波长为0.1,0.2,0.3和0.4 m时弹条的动应力响应。图11是弹条应力幅值随短波波长变化曲线。表3列出了4种波长条件下弹条动应力幅值和突变应力幅值。由图11和表3可知,波长从0.4 m减小到0.2 m时弹条动应力幅值和突变应力幅值平缓增加;当波长由0.2 m减小到0.1 m时两者快速增长,特别是弹条突变应力幅值急剧增加约94%,是波长为0.4 m时的2.4倍。

图11 弹条应力幅值与短波波长的关系
波长/m动应力幅值/MPa突变应力幅值/MPa0.1136.987.50.2110.445.10.3100.339.00.497.436.8
5结论
建立弹条Ⅱ型扣件有限元模型,开展了扣件安装受力分析和30 t轴重货车以80 km/h速度通过钢轨焊接不平顺时弹条的动应力响应分析,得到以下研究结论:(1)扣件安装到位后扣压力为10.2 kN,弹程为10.7 mm,满足弹条Ⅱ型扣件铺设安装规范要求;弹条后弯肢内侧表面出现轻微局部塑性屈服,表面屈服深度最大约0.4 mm,与工程实际基本吻合,说明本文建立的扣件有限元模型能够较准确模拟弹条的应力应变状态。(2)轮对通过焊缝不平顺瞬间,弹条高频突变应力幅值较大,这将加快焊缝区弹条疲劳损伤。弹条动应力幅值和突变应力幅值均随焊缝不平顺波深增大而线性增大,随波长的减小而加速增大,特别是波长小于0.2 m以后,弹条突变应力幅值急剧增大。为了降低焊缝区弹条动应力幅值,有必要严格控制波长0.2 m以下焊缝不平顺。
参考文献
[1]于春华. 铁路钢轨扣件发展综述[J]. 铁道标准设计, 2006, (S1): 188-191.
[2]奚绍良, 龚佩毅, 俞峰. 弹条Ⅲ型扣件性能测试与分析[J]. 铁道标准设计, 2002, (7): 8-11.
[3]武青海, 陈厚娥, 周虹伟, 等. 应用非线性接触理论分析弹条Ⅲ型扣件中弹条的应力和变形[J]. 中国铁道科学, 2003, 24(1): 69-73.
[4]杨吉中, 潘自立, 田春香. 弹条材质对扣件性能参数的影响分析[J]. 高速铁路技术, 2012, 3(4):15-18.
[5]朱胜阳, 蔡成标, 尹镪, 等. 高速铁路扣件弹条动力学分析[J]. 工程力学, 2013, 30(6): 254-287.
[6]MOHAMMADZADEH S, AHADI S, NOURI M. Stress-based fatigue reliability analysis of the rail fastening spring clip under traffic loads[J]. Latin American Journal of Solid and Structures, 2014, 11(6): 993-1011.
[7]中华人民共和国铁道部. TB/T 3065.1-2002 弹条Ⅱ型扣件[S]. 北京: 中国铁道出版社, 2002.
[8]罗晓勇. Ⅲ型弹条扣压力的研究及应用[J]. 铁道标准设计, 2002, (6): 15-16.
[9]翟婉明.车辆-轨道耦合动力学(第四版)[M]. 北京:科学出版社, 2015.

Effect of Rail Weld Irregularities on Dynamic Stress of Fastening Spring Clip
LIU Xiao - jun, ZHAO Chun - fa, ZHANG Xu
(StateKeyLaboratoryofTractionPower,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China)
Abstract:A finite element model (FEM) of the spring clip type II fastening has been established, and dynamic stress analysis of the spring clip has been carried out considering various wavelength and wave depth of rail weld irregularities. Numerical results show that mechanical performance indexes of the fastening meet the installation requirement when it is installed in right place, the inside surface layer of spring clip at rear bent part appears slight local plastic yielding. It means the FEM model of fastening can simulate correctly stress states of the spring clip. Comparing to the smooth rail, dynamic stress amplitude of the spring clip increases remarkably when the rail have the weld irregularity, and it will accelerate fatigue damage of the spring clip. Both dynamic stress amplitude of spring clip and the abrupt stress amplitude increases linearly with the wave depth of weld irregularity; in addition, they increase slowly with the decrease of the wavelength of the weld irregularity firstly, then increase rapidly since the wavelength is smaller than 0.2 m.
Key words:Fastening spring clip; Dynamic stress; Rail irregularity; Nonlinear contact; Finite element method
中图分类号:U213.2
文献标志码:A
文章编号:1671-8755(2015)04-0020-05
作者简介:刘小军(1989—),男,硕士生,研究方向为轨道结构力学与疲劳伤损。E-mail:swjtuliuxj@163.com
基金项目:国家自然科学基金(51578469,51478399);牵引动力国家重点实验室自主研究课题(2015TPLT12)。
收稿日期:2015-07-01
