锦屏一级高拱坝坝肩刚体弹簧元动力抗滑稳定分析
2016-01-21黄志刚张建海吴玉龙薛利君
黄志刚 周 钟 张建海 吴玉龙 薛利君
(1.四川大学水利水电学院水力学及山区河流开发与保护国家重点实验室 四川成都 610065;
2. 中国电建成都勘察设计研究院有限公司 四川成都 610072)
锦屏一级高拱坝坝肩刚体弹簧元动力抗滑稳定分析
黄志刚1周钟2张建海1吴玉龙1薛利君2
(1.四川大学水利水电学院水力学及山区河流开发与保护国家重点实验室四川成都610065;
2. 中国电建成都勘察设计研究院有限公司四川成都610072)
摘要:锦屏一级水电站地质条件复杂:拱坝右岸由特定结构面f13断层、f14断层及SN向裂隙参与形成了7个控制滑块;左岸为反向坡,存在煌斑岩脉、f2断层、f5断层、f8断层、f42-9断层且左岸坝肩松弛严重,左岸坝肩稳定是关键性的技术问题。利用刚体弹簧元法对锦屏一级高拱坝左、右岸坝肩控制滑移块体进行了地震动力稳定分析。通过计算分析,左岸最小动安全系数出现在L5滑块且其Kd为1.434,右岸最小动安全系数出现在R4-3滑块且其Kd为2.166,拱坝的坝肩抗滑动安全系数均在合理范围内,其左右岸坝肩均能满足稳定性要求。
关键词:拱坝刚体弹簧元控制滑块地震动力分析
Rigid Body Spring Element Method for Dynamic Anti-sliding
1工程概况
锦屏一级水电站[1]位于四川省凉山彝族自治州盐源县和木里县境内,是雅砻江干流下游河段(卡拉至江口河段)的控制性水库梯级电站,主要任务是发电。电站总装机容量360万kW(6台×60万kW),多年平均年发电量166.2亿kW·h,总库容77.6亿m3,调节库容49.1亿m3,多年平均年径流量385亿m3,属年调节水库。
锦屏一级水电站拱坝坝高305 m,为世界第一高拱坝[2],右坝肩及抗力体位于Ⅱ1线至Ⅳ线约450~500 m范围内,地形完整,无沟谷发育,山体雄厚,谷坡陡峻。1 810 m高程以下谷坡陡峭,坡度70°以上,局部为倒坡;1 810 m高程以上坡度较缓,自然坡度40°~50°,为大理岩组成的顺向坡。
左坝肩及抗力体范围内I线1 900 m高程、V线1 880 m高程、II线1 840 m高程以下为大理岩,地形陡立,坡度60°~80°,上述高程以上为砂板岩,地形坡度变缓至45°左右。f2断层产状较可研阶段有所变化,f2断层产状采用N25°E,NW∠35°~40°。锦屏一级水电站坝址区基本烈度为Ⅶ度[3],100年超越概率2%时为0.27g。鉴于锦屏高拱坝地质复杂性、超高坝高及较高地震烈度,其坝肩动力稳定性为该工程的关键技术问题。
本文采用刚体弹簧元法[4]研究锦屏一级拱坝的地震反应分析及坝肩稳定[5],研究了大坝的地震动位移、速度、加速度,得出地震反应的相关结论。
2计算原理
2.1基本原理
本文计算采用刚体弹簧元模型[6-7](RBSM:Rigid Body-Spring Model),其基本思想是把结构划分为一些由分布在接触面上的弹簧系统连接在一起的刚性单元的集合,传统有限元强调几何协调性,这种模型常常不宜用于模拟错动等岩石变形特点。四川大学水电学院岩土教研室研制开发的二维、三维刚体元数值分析软件,可处理多种荷载情况(包括体力、面力、集中力、变温、地震力)作用下的静动力分析计算,除了常规的位移和力,动力计算[8]中还输出:特征频率及振型,位移、速度、加速度,动应力,动安全系数,等等。
2.2分析原理
动力方程:
(1)

C=αM+βK
(2)
其中α,β为比例系数,对于式(2),求解动力方程的常用解法有振型叠加法、直接积分法,因为坝肩处有不同产状的断层,坝肩岩层为非线性的特点,所以选用NewMark积分法。
2.3控制滑块的边界
左岸由f5断层、f8断层、煌斑岩脉、深部裂缝、f2断层和顺层挤压带形成了5个控制滑块,右岸由特定结构面f13断层、f14断层及SN向裂隙参与形成了7个控制滑块。限于篇幅,文章着重分析了R4-3 和L5滑块的稳定性,其滑块网格见图1、图2,其力学参数见表1,其控制块体的组合及产状见表2。

图1 右岸滑块R4-3
图2 左岸滑块L5

块体编号滑面编号侧滑面剪摩f'C/MPa滑面编号底滑面剪摩f'C/MPaR4-3P10.30.02P21.0181.169P30.7230.634L50.250.30.020.250.30.02

表2 控制块体组合及产状表
注:底滑面P2与建基面交点高程指的是底滑面P2与建基面上游侧交点,左坝肩滑块是一陡一缓滑动面形成的块体。
右坝肩滑块体中NWW向裂隙距上游拱端的距离300 m,底滑面P2与建基面交点高程为1 732.00 m。由于f5断层和f8断层在拱坝轴线下游的产状基本一致、位置相近,部分范围内甚至重合,故在计算分析中均把f5断层和f8断层当作同一个侧滑面来考虑。
2.4动力抗滑安全系数
岩土材料动力参数的确定、地震波在岩层中的传播逸散及衰减的定量分析、结构物与地基的耦合作用[9]等许多问题尚在分析研究中。限于岩土材料动力参数的缺乏,在动安全系数推求中往往仍采用静强度。
在刚体元地震动力分析中,可以求得任意时刻交界面上的正应力和剪应力,因而可以积分得到任意时刻滑动体上的下滑力和总的阻滑力,从而求得该时刻的瞬时安全系数。从时间维上来看,随着地震波的传播及逸散,岩体内各点应力随之变化,因而滑动体瞬时安全系数亦随时间发生变化。用刚体元法求得的动安全系数将是一条曲线,而不再是一个定值。这与传统刚体极限平衡法计入地震作用的方法相比更为合理。下面简述刚体元推求安全系数的基本思想:首先求得研究域的初始静应力场σs,在动荷载作用下,各点应力将因地震作用而产生附加动应力场σd,由此得到各时刻总应力场σt,即:
σt=σs+σd
(3)
刚体元单元交界面上正应力σn及剪应力τs,τt均为时间t的函数。故在动力情况下,安全系数将不再是一个定值,其量值可由下式求得[7]:
(4)
3研究实例
3.1计算模型
锦屏高拱坝三维刚体弹簧元分析计算范围取为:X方向由左岸指向右岸,拱坝中心线两侧各取600 m,即横河向截取1 200 m。Y方向由上游指向下游,拱坝轴线上游侧取294.24 m,顺河向截取总长度1 302.0 m。铅直向底部取至▽1 280.0 m高程,顶部延伸至坝顶1 885 m高程。为能充分模拟地形地质特征和坝肩大垫座等结构,本次网格划分采用了46个平切面,三维计算模型共计剖分节点13 970,刚体单元13 514,图3给出了三维网格图。

图3 刚体弹簧元计算模型(下游视图)
3.2计算工况和参数
计算工况:正常蓄水位+自重+淤沙+温降+渗透压力(帷幕排水设施正常)。对上述计算工况采用地震波输入法进行动力计算,其中正常蓄水位取1 880.00 m,对应下游水位是1 645.00 m。对于作用于坝肩滑块侧滑面和底滑面上的渗压,则由成勘院提供的渗流自由面经过坐标插值变换后得到,各岩类计算参数参见表3。

表3 计算参数
注:X1,1 750 m以上同Ⅳ2;X2,1 750 m以下同Ⅲ2;断层,同Ⅴ1。
3.3输入地震参数
图4-图6所示为本次计算输入的100年超越概率2%,ahmax=0.27g的锦屏一级人工地震波(规范谱)。竖向峰值加速度取为水平向的2/3,计算时间步取为0.02 s。

图4 锦屏一级X方向输入地震波

图5 锦屏一级Y方向输入地震波

图6 锦屏一级Z方向输入地震波
4计算结果与分析
4.1地震作用下的位移
计算输出量包括各特征单元位移、速度、加速度的变幅,总结了各特征值与高程的关系。在地震荷载作用下,高程较高的单元具有较大的动位移,如图7所示为拱坝特征单元的顺河向动位移图。
沿着顺河向和横河向随着高程降低,动位移幅值也随之下降,坝顶拱冠处单元12 167顺河向振幅最大可达10.16 cm。1 870 m左右拱端的顺河向动位移极值量值接近,左拱端动位移极值4.754 cm,右拱端动位移极值4.988 cm。1 740 m高程左拱端动位移极值3.018 cm,右拱端顺河向动位移极值3.722 cm。

图7 拱坝特征单元的顺河向动位移图
4.2地震作用下的速度
计算表明,在地震荷载作用下,高程较高的单元具有较大的速度,如图8以特征单元顺河向速度为例。沿着顺河向和顺河向随着高程降低,速度值也随之下降,坝顶拱冠处单元12 167顺河向速度极值1.712 m/s。1 870 m高程左拱端顺河向速度极值0.349 3 m/s,右拱端顺河向速度极值0.337 m/s。1 740 m高程左拱端顺河向速度极值0.227 8 m/s,右拱端顺河向速度极值0.244 8 m/s。坝踵1 580 m处单元为0.084 48 m/s。1 135 m左右拱端的速度极值量值接近,右拱端速度极值0.489 8 m/s,左拱端速度极值0.563 3 m/s。

图8 拱坝顺河向特征单元的速度图
4.3地震作用下的加速度
计算表明,在地震荷载作用下,高程较高的单元具有较大的加速度,如图9以特征单元顺河向加速度为例。例如坝顶拱冠处单元12 167顺河向加速度最大可达14.319 m/s2,1 870 m高程的左拱端速度极值4.665 m/s2,右拱端加速度极值2.886 m/s2。1 740 m右拱端加速度极值3.33 m/s2,左拱端速度极值3.081 m/s2,坝踵1 580 m处单元为1.713 m/s2。

图9 拱坝顺河向特征单元的加速度图
4.4地震作用下的交界面应力
图10是几个交界面正应力的初始值和极值的变化图,其中变幅最大的是坝踵处的特征界面,正应力变幅值达到了6.600 7 MPa。
在输入地震波作用下的正应力和剪应力时间历程中,交界面的正应力和剪应力处于一个波动的范围。以坝踵底滑面正应力4 393为例,静力状态下,该交界面处于压应力状态,正应力σn=-1.898 5 MPa,地震波作用下,其动应力幅值在-5.303 1至1.297 6 MPa之间波动。
图11为交界面JX4393的正应力响应曲线。

图10 拱坝特征交界面正应力图

图11 交界面JX4393的正应力响应
4.5动力抗滑稳定安全系数
本次动力研究的初始静应力以工况(自重+正常蓄水+温降+帷幕排水正常)为基准,拱坝坝肩各滑块在地震波作用下的动力安全系数见表4。

表4 锦屏一级高拱坝坝肩动力稳定安全系数

左岸滑块L5由f5(f8)断层为侧滑面、f2断层为底滑面形成的一陡一缓滑动块体。在地震作用下,左岸L1滑块安全系数由7.71的静力值降至1.434的最小动力安全系数,降幅6.276。图13为左岸控制滑移块体为L5的动安全系数历程。

图12 滑块R4-3动力安全系数历程
综上可知:地震作用下,左右岸滑块动安全系数均大于规范值,最小动安全系数出现在左岸L5,其Kd=1.434。故锦屏一级高拱坝左右岸滑块均能满足稳定性要求。
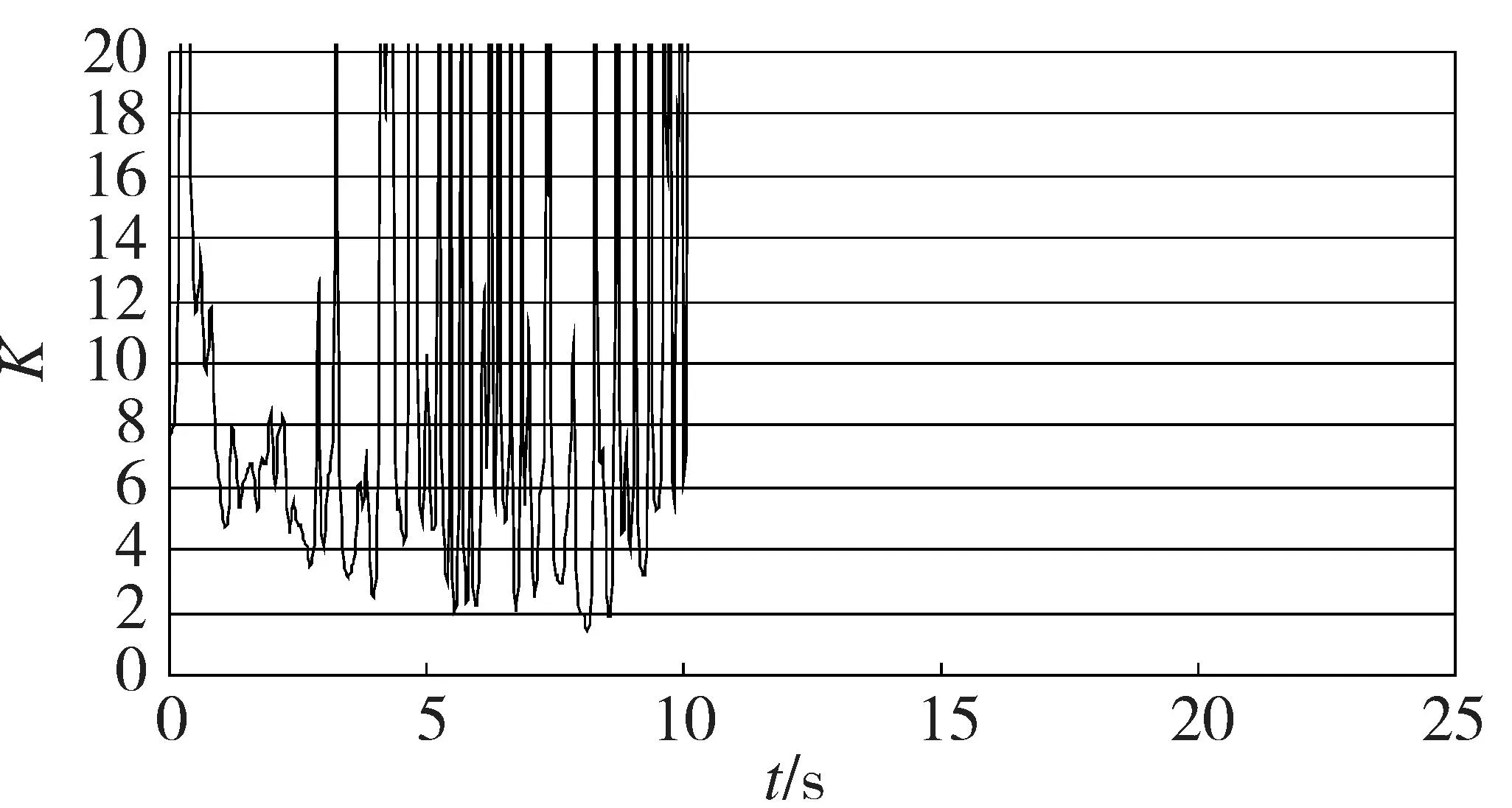
图13 滑块L5动力安全系数历程
5结论
采用三维刚体弹簧元法对锦屏一级高拱坝开展了应力应变和左右岸控制滑移块体动力稳定性研究,得到以下结论:(1)随着高程降低,动位移幅值、加速度、速度也随之下降。在100年超越概率2%,amax=0.27g的人工地震波作用下顺河向坝顶拱冠处振幅最大可达10.16 cm,加速度最大可达14.319 m/s2,速度最大可达1.712 m/s。1 740 m高程左拱端动位移极值3.018 cm,1 030 m高程左拱端加速度极值4.331 m/s2,1 030 m高程左拱端速度极值0.331 3 m/s。(2)地震作用下,左右岸滑块动安全系数均大于1.0,最小动安全系数出现在左岸L5,其Kd=1.434,故锦屏一级高拱坝左右岸滑块均能满足稳定性要求。(3)尽管锦屏一级高拱坝左右岸控制滑移块体的动力安全系数较大,不会发生大块体动力失稳破坏,考虑到河谷陡峻,岸坡卸荷松弛严重,在地震波作用下,边坡浅表岩体的稳定性问题突出,易于产生环境边坡危岩体垮塌,建议做好环境边坡治理。
参考文献
[1]国家电力公司成都勘测设计研究院.雅砻江锦屏一级水电站可行性研究报告-工程地质[Z]. 2003.
[2]潘家铮.拱坝[M].北京:水利电力出版社,1982.
[3]M.维兰德,胡云鹤. 地震反应监测与大坝安全监测[J].地震与大坝安全, 2011, 32(2):33-36.
[4]张建海,范景伟,胡定.刚体弹簧元理论及应用[M]. 成都:成都科技大学出版社,1999.
[5]刘小强.高拱坝坝肩稳定分析及复杂地质缺陷概化模型研究[D].成都:四川大学研究生论文,2005.
[6]张建海,范景伟,胡定.刚体弹簧元理论及应用[M]. 成都:成都科技大学出版社,1999.
[7]张建海,范景伟,何江达.用刚体弹簧元法求解边坡、坝基动力安全系数所示[J].岩土力学与工程学报,1999,18(4):387-391.
[8]DL5073-2000,水工建筑物抗震设计规范[S].北京:中国电力出版社,2001.
[9]陈啸, 刘斌, 席广恒, 等. 结构-地基耦合震动下地震反应谱特性[J]. 内地地震, 2006, 20(4):324-329.

Analysis of Jinping I Arch Dam Abutment
HUANG Zhi-gang1,ZHOU Zhong2,ZHANG Jian-hai1,
WU Yu-long1,XUE Li-jun2
(1.StateKeyLaboratoryofHydraulicsandMountainRiverandProtection,CollegeofWater
Resources&Hydropower,SichuanUniversity,Chengdu610065,Sichuan,China;2.ChineseHydropower
EngineeringConsultingGroupChengduDesign&ResearchInstitute,Chengdu610072,Sichuan,China)
Abstract:Jinping I Hydropower Station is in complex geological conditions. Investigation showes that the controlling blocks of the right bank of the arch dam are formed by specific structural plane f13 fault, f14 fault and the crack of SN orientation, while the slope of the left bank is reverse with lamprophyre veins, f2, f5, f8, f42-9 faults. In addition, the left bank abutment is highly relaxed. All of this make the abutment stability of left bank to be a critical technical problem. The rock faults and discontinuous deformation characteristics can be expediently simulated by using the rigid body-spring element method, and then the analysis of the seismic dynamic stability for the controlling sliding block of the left and the right abutment can be performed. Through calculation and analysis, the minimum dynamic safety coefficient (Kd) of left bank appears in the L5 slider and the value is 1.434; the right bank is R4-3 slider and its value is 2.166. All safety coefficients of arch dam abutment sliders are reasonable and all the abutments can satisfy the stability requirement.
Key words:Geological conditions; Rigid body-spring element; Controlling slider; Power calculation; Safety coefficient
中图分类号:TV642.4
文献标志码:A
文章编号:1671-8755(2015)04-0093-07
作者简介:黄志刚(1991—),硕士研究生,研究方向为岩土数值模拟、大坝与基础工程。E-mail:huangzhigangsm@163.com
收稿日期:2015-07-01
