30 t轴重货车-重载铁路车轮扁疤动力效应分析
2016-01-21张大伟王开云翟婉明
张大伟 王开云 翟婉明
(西南交通大学牵引动力国家重点实验室 四川成都 610031)
30 t轴重货车-重载铁路车轮扁疤动力效应分析
张大伟王开云翟婉明
(西南交通大学牵引动力国家重点实验室四川成都610031)
摘要:基于车辆-轨道耦合动力学理论,针对30 t轴重货车和重载铁路轨道结构,研究了新、旧扁疤作用下的轮轨动力作用特征,并对两种扁疤形式的最大允许限值提出了相应的建议。结果表明:新扁疤作用下,轮轨垂向力会出现典型的高频作用力和低频作用力,根据英国铁路轮轨冲击力的限值标准,新扁疤长度的最大允许限值建议采用37 mm;旧扁疤作用下,轮轨垂向力不再出现高频作用力和低频作用力,代之以最大轮轨作用力出现,结合美国铁路工程协会关于动荷载系数2.0的标准和轮重减载率0.8的限值,旧扁疤长度最大允许限值建议采用45 mm。
关键词:重载铁路车轮扁疤车辆-轨道耦合理论30 t轴重货车
由于轮对的长期使用,车轮踏面不可避免地出现擦伤或剥离等现象,统称为车轮扁疤。车轮存在扁疤时,车轮形状不能保持为正圆,随着车轮的旋转,这种扁疤将对轮轨系统造成很大的冲击作用,随之而产生周期性的轮轨作用力。同时,随着我国重载铁路的发展,轴重逐渐增大,势必对轮轨动态相互作用提出新的挑战。为了降低轮轨动力作用,应该对重载铁路提出更严格的标准,以提高重载轨道结构以及重载车辆的长期服役性能,降低生产维护成本。长期的实践证明,重载列车在运行过程中不可避免地产生车轮踏面擦伤和剥离,引起轮轨动态作用恶化。
对于车轮扁疤的研究,早期,国内学者王其昌[1]分析了不同行车速度下扁疤导致的冲击速度,得到在临界速度20~30 km/h存在最大冲击速度,且在列车速度10~60 km/h范围内,扁疤车轮的动力影响最大。随后,翟婉明[2]应用车辆-轨道耦合理论分析了车轮扁疤冲击的基本特征,并确定了C62A货车车轮扁疤一处的限制长度为42 mm。随着车轮扁疤研究的深入,王建斌等[3]研究了车轮扁疤引发附加冲击力对车轴应力谱影响,为疲劳可靠性评定提供了依据。杨新文等[4]研究了车轮扁疤产生的轮轨噪声。而随着高速铁路的发展,王忆佳等[5]利用多体动力理论研究了新、旧扁疤产生的动力作用,得出当车速分别高于200 km/h和250 km/h时,车轮扁疤长度需要限制在35 mm和30 mm以内。国外,SACKFIELD A[6]对车轮新扁疤进行了细致的建模,研究了扁疤存在下的轮轨接触行为。而PIERINGER A等[7]则建立了二维和三维两种扁疤轮轨接触模型,并以此分析了扁疤存在下的轮轨冲击行为。
综上可知,对于重载货车的研究还比较少,刘建新等[8]仅分析了25 t轴重货车新、旧扁疤的轮轨动力作用的不同,对于重载货车扁疤的限值研究并无涉及,且30 t轴重货车在扁疤条件下的动力效应目前尚不明确,亟需针对30 t轴重条件制定相应的扁疤长度限值标准,以适应重载铁路的发展。本文从大系统角度出发,针对30 t轴重货车和重载轨道结构,开展大轴重货车扁疤动力效应的分析,以期为大轴重货车制定相应的扁疤控制标准提供理论参考。
2理论分析模型
2.1车辆-轨道耦合动力学模型
车辆-轨道耦合动力学理论的基本思想[9]是将车辆系统和轨道系统视为一个相互作用、相互耦合的整体大系统,将轮轨相互作用关系作为连接这两个子系统的“纽带”。本文基于该理论,给出了30 t轴重重载货车与有砟轨道动态相互作用分析模型,如图1所示。
30 t轴重货车采用“三大件”式转向架,车体和转向架之间通过旁承和心盘连接。针对其结构特点,将货车系统简化为由车体、摇枕、侧架、轮对等11个部件组成的多刚体系统,每节车共47个自由度。在摇枕和车体间考虑心盘和旁承提供的回转摩擦副,垂向和横向悬挂直接等效到车体和侧架之间,考虑摇枕的摇头自由度,其余自由度和车体一起考虑;侧架和摇枕之间考虑摇枕弹簧的垂向、横向与纵向刚度以及楔块摩擦阻尼特性;轴箱悬挂在横向和纵向考虑轴箱间隙,在轴箱间隙范围内,用一个弹簧阻尼器来模拟;当轴箱与侧架接触后,用弹簧阻尼器与线性弹簧止档并联来模拟;侧架考虑纵向、横向、垂向、摇头和点头自由度。

图1 30 t轴重货车-轨道耦合动力学模型
重载铁路有砟轨道由钢轨、扣件、钢筋混凝土轨枕及道床等组成,轨道模型采用“翟-孙五参数模型”[9]。钢轨视为有限长Euler梁模型,考虑其垂向、横向振动及扭转振动;轨枕视为刚体并考虑其垂向、横向运动及转动自由度,钢轨与轨枕以及轨枕与道床之间通过线性弹簧和黏性阻尼连接。道床按轨枕实际间距离散成质量块,考虑其垂向振动。道床与路基之间同样通过线性弹簧和黏性阻尼连接,通过道床质量块之间的剪切刚度和阻尼来模拟道砟的啮合作用。
2.2扁疤物理模型
车轮扁疤在滚动过程中将产生特殊的动力效应,且新、旧扁疤产生的作用机理也不一致。图2给出了新、旧扁疤的具体形貌,新扁疤同踏面上圆周上的弦线相似,而旧扁疤则是新扁疤磨圆后的结果,这时旧扁疤可简单的用余弦函数描述。

图2 车轮扁疤模型
由车轮新扁疤引起的冲击速度公式[9]为
(1)
μ=(Mc+4Mt+4Mw)g/4Mw
(2)
(3)
式(1)-(3)中,μ为车轮向下跌落的加速度,v为车辆运行速度,vcr为车轮扁疤冲击的临界速度,R为车轮半径,L为车轮扁疤长度,γ为车轮旋转惯量转换为往复惯量系数,Mc,Mt和Mw分别为车体(含摇枕)、侧架和轮对质量。
在实际运营中,理想的新擦伤并非经常出现,且一旦出现,经过一段时间运行后,车轮擦伤棱角受冲击荷载作用而很快被磨圆。因此,实际中车轮旧扁疤不平顺大多可近似用余弦函数来表示:
Z=0.5a[1-cos(2πx/L)]
(4)
式中,a是有效擦伤深度,且有a=L2/16R。
1.3国内外标准
1.3.1车轮踏面扁疤
根据我国《铁路技术管理规程》的规定,货车车轮踏面扁疤的容许限度标准之一是:车轮踏面擦伤及局部凹下≤1 mm,车轮踏面剥离长度一处为50 mm,二处为40 mm。这里取两者的最高标准,检验30 t轴重货车行驶过程中是否能够满足该要求。对于半径为0.4 575 m重载车辆专用车轮,1 mm踏面擦伤相当于60.5 mm的扁疤长度,小于踏面剥离长度标准,因此,这里取50 mm的扁疤长度作为检验标准。
1.3.2轮轨垂向力
英国铁路(BR)规定了机车车辆通过钢轨低接头等瞬态冲击作用时的轮轨垂向力P1和P2的限值标准:
(5)
该标准仅适用于冲击作用下的轮轨垂向力评价,对于常规激扰,如轨道随机不平顺下的轮轨垂向力的评价并不适用。目前,对于重载货车轮轨垂向力的标准限值,国内并无相关标准,而国外常以设计荷载系数来确定最大轮轨力。因此,这里介绍两个主要的标准[10],分别为艾森曼公式和英国铁道研究中心的动荷载系数计算公式。
艾森曼公式基于统计学原理,动荷载系数的计算公式为:
φ=1+δ·η·t
(6)
式中,δ表示轨道状态系数,取值如下:δ=0.1,轨道处于极好状态;δ=0.2,轨道处于良好状态;δ=0.3,轨道处于较差状态。η表示速度系数,取值如下:η=1,列车速度v不高于60 km/h;η=1+(v-60)/140,列车速度v在60~200 km/h之间。t决定于置信区间的标准差乘数因子,取值如下:t=0,置信区间上限50%;t=1,置信区间上限84.1%;t=2,置信区间上限97.7%;t=3,置信区间上限99.9%。
英国铁道研究中心的动荷载系数计算公式只考虑了钢轨接头、列车运行速度、簧下质量和轨道不平顺等因素,主要用于计算接头处的轮轨冲击作用,其公式为:

(7)
式中,α1+α2为轨道连接总倾角(弧度),英铁取为0.015;Pu为静轮载(kN);Dj为连接处轨道刚度(kN/mm),英铁取为88 kN/mm;Ps为单轮簧下重量(kN);g为重力加速度(m/s2)。
图3给出了上述两种动荷载系数随速度的变化关系图,艾森曼公式中3种状态在图中很好地展示出来。在货车运行速度80 km/h内,两种规定的动荷载系数均不大于2.0,与美国铁路工程协会规定的最大轮轨垂向力为静轮载的2.0倍相一致。
因此,对于新扁疤作用下的冲击作用,本文采用BR对轮轨垂向力P1和P2提出的限值标准,而对于旧扁疤作用下轮轨动力作用,采用美国铁路工程协会关于动荷载系数2.0的标准,即300 kN作为轮轨垂向力最大限值。
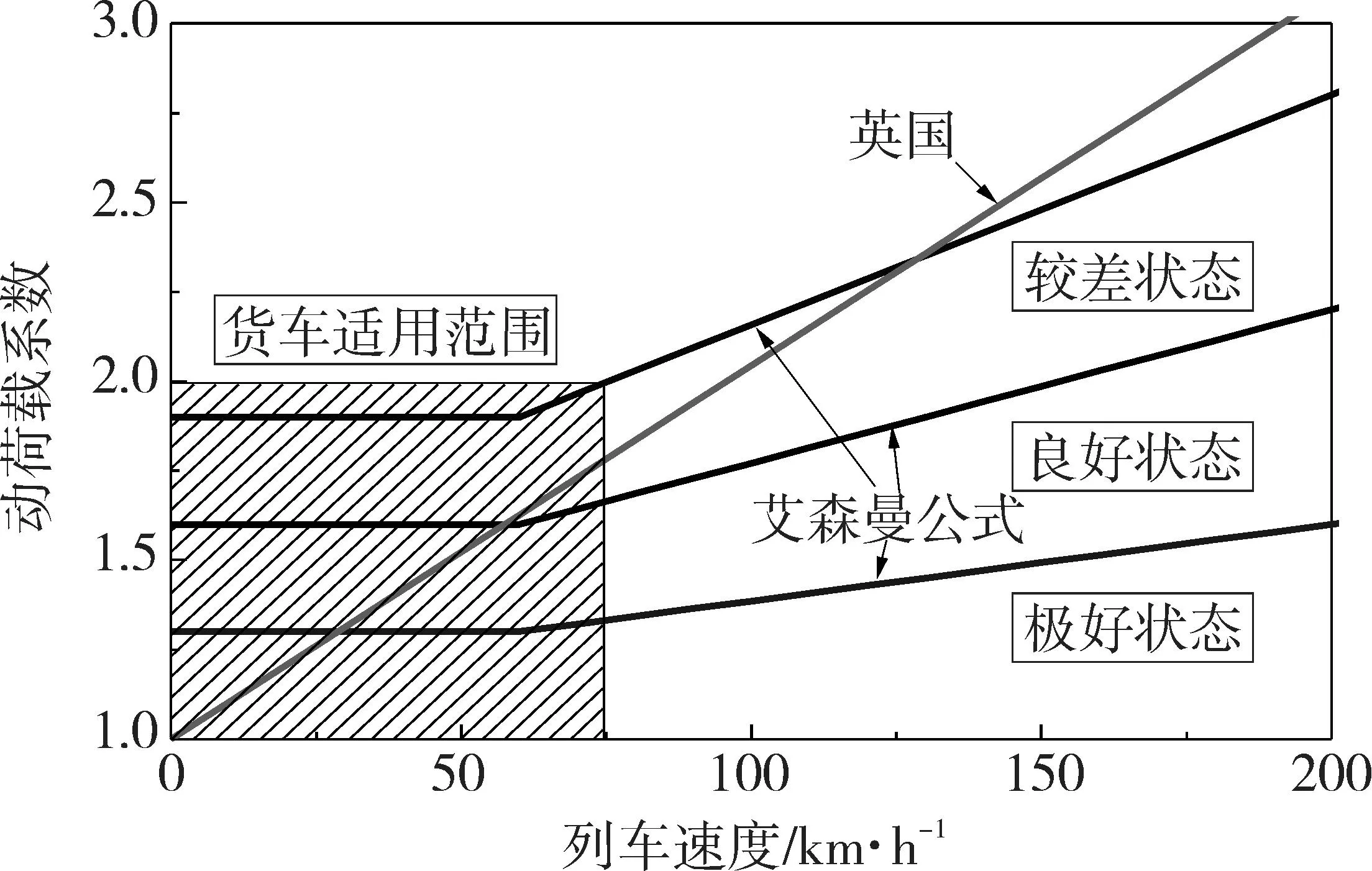
图3 动荷载系数分布图
3重载铁路车轮扁疤动力效应
为了研究重载铁路车轮扁疤的轮轨动力特性,选用某厂生产的30 t轴重货车作为研究对象,行车速度为60 km/h,车轮半径为0.457 5 m,扁疤长度在20~120 mm范围内。
3.1新扁疤动力效应
不同新扁疤长度下的轮轨冲击效应如图4所示。以扁疤长度为40 mm下的轮轨垂向力时程响应为例,轮轨力在整个时间历程中产生了两个峰值,按英国铁路的定义,称之为P1,P2力。P1力为高频作用力,相当于Hertz接触振动频率,而P2力为中低频作用力,此时P1,P2力分别为436 kN,224 kN,可见,P1力远大于P2力。由图5还可以看出,随着扁疤长度的增加,P1,P2力快速增大,当扁疤长度为60 mm时,P1,P2力均超过了BR规定的标准,这种巨大的轮轨作用力将对轨道结构产生显著的破坏作用,造成轨道结构服役周期缩短以及养护维修成本增加,因此对于这种扁疤缺陷的控制就显得十分重要。

图4 新扁疤激扰下的轮轨垂向力响应
图5给出了P1力和P2力随扁疤长度的变化规律,两者均与扁疤长度呈线性递增关系。当扁疤长度为50 mm时,P1,P2力分别为516 kN,250 kN,P2力恰好满足BR的标准,而P1力已远大于BR的控制标准。为此,图5还按照BR对P1,P2的规定给出了相应限值,此时P1对应的最大允许扁疤长度为37 mm,P2对应的最大允许扁疤长度为50 mm,综合两者可得到最后的扁疤长度最大限值为37 mm。新的控制标准要小于《铁路技术管理规程》的标准:擦伤限值60.5 mm和剥离限值50 mm。

图5 轮轨垂向力与新扁疤长度的关系
3.2旧扁疤动力效应
新扁疤圆化后发展成为平滑的旧扁疤,其引起的轮轨动力响应如图6所示。旧扁疤引起的轮轨动力响应与新扁疤明显不同,此时,已无P1和P2力激发出来,代之以最大作用力Pmax。同时,不同扁疤长度对应的轮轨垂向力响应也明显不同。图6(a)给出了扁疤长度较小时的轮轨动力响应,扁疤长度由20 mm增加到60 mm,最大轮轨垂向力逐渐增大,且不会出现轮轨脱离,但当扁疤长度为40 mm时,轮轨垂向力已经超过既有标准(250 kN)。图6(b)给出了扁疤长度进一步增大时轮轨动力响应结果,随着扁疤长度的增大,将发生轮轨脱离的现象。当扁疤长度在80~100 mm范围内时,仅发生一次轮轨脱离现象,但当扁疤长度继续增大到120 mm时,将发生两次轮轨脱离现象,且最大轮轨脱离时间达5 ms。
不同旧扁疤长度激扰下得到的最大轮轨垂向力的变化规律如图7所示。扁疤长度小于60 mm时,最大轮轨垂向力随扁疤长度的增加而缓慢增大;而在扁疤长度大于60 mm时,最大轮轨垂向力随扁疤长度的增加而快速增大。按照美国铁路工程协会轮轨垂向力300 kN的限值,可得到扁疤长度最大允许限值为45 mm。而当按照《技术管理规程》的扁疤长度限值50 mm的要求时,最大轮轨力已达315 kN,超过美国铁路工程协会300 kN的限值。同时,若以250 kN作为控制标准得到的扁疤长度限值仅为25 mm,远小于40 mm的标准。综上可知,以300 kN作为控制标准是较为合理的,在此标准下,扁疤长度最大允许限值为45 mm。

图6 旧扁疤激扰下的轮轨垂向力响应

图7 轮轨垂向力与旧扁疤长度的关系
图8给出了轮重减载率与旧扁疤长度的对应关系,随着扁疤长度的增加,轮重减载率逐渐增大,当扁疤长度大于70 mm时,轮重减载率将达最大值,出现轮轨完全脱离现象。我国南津浦线货车脱轨试验中规定的轮重减载率为0.8,因此本文将0.8作为轮重减载率的限值。扁疤长度50 mm,45 mm和25 mm对应的轮重减载率分别为0.46,0.8和0.9,可见,45 mm扁疤长度下的轮重减载率刚好达到限值要求,25 mm扁疤长度对应的轮重减载率仅为0.46,偏于保守,而50 mm扁疤长度对应的轮重减载率已达0.9。因此,从轮重减载率的角度来看,45 mm 扁疤长度的控制标准是比较合理的。

图8 轮重减载率与旧扁疤长度的关系
3结论
本文基于车辆-轨道耦合动力学理论,针对30 t 轴重货车和重载铁路轨道结构,分析了新、旧扁疤作用下的轮轨作用特征,并结合相应规定,对两种扁疤形式最大允许限值提出了相应建议。
(1)新扁疤作用下,轮轨作用力会出现典型的高频作用力P1和低频作用力P2,且两者均随车轮扁疤长度的增大而迅速增大。
(2)旧扁疤作用下,轮轨作用力不再出现P1和P2力,代之以最大轮轨作用力Pmax出现,当扁疤长度达到一定值后,会出现轮轨分离现象,且随扁疤长度的增加,轮轨最大作用力先缓慢增大后快速增加。
(3)以BR最大P1力为标准得到新扁疤长度限值为37 mm,而以美国工程协会制定的动荷载系数2.0为标准得到旧扁疤长度限值为45 mm。
参考文献
[1]王其昌. 车轮扁疤冲击分析[J]. 西南交通大学学报, 1991, 26(4): 45-48.
[2]翟婉明. 铁路车轮扁疤的动力学效应[J]. 铁道车辆, 1994,(7): 1-5.
[3]王建斌, 邬平波, 唐兆. 车轮扁疤引发附加冲击力对车轴应力谱影响的研究[J]. 铁道学报, 2006, 28(1): 39-43.
[4]杨新文,翟婉明. 车轮扁疤激起的轮轨冲击噪声机理分析[J]. 振动与冲击, 2009, 28(8):46-49.
[5]王忆佳,曾京,高浩,等. 车轮扁疤引起的轮轨冲击分析[J]. 西南交通大学学报, 2014, 49(4): 700-705.
[6]SACKFIELD A, DINI D, HILLS D A. The contact problem for a wheel having a ‘flat’[J]. Wear, 2006, 261(11): 1265-1270.
[7]PIERINGER A, KROPP W, NIELSEN J C O. The influence of contact modelling on simulated wheel/rail interaction due to wheel flats[J]. Wear, 2014, 314(1): 273-281.
[8]刘建新,易明辉,王开云. 重载铁路车轮踏面擦伤时的轮轨动态相互作用特征[J]. 交通运输工程学报, 2010, 10(3): 52-56.
[9]翟婉明. 车辆-轨道耦合动力学(上册)[M]. 第4版. 北京: 科学出版社, 2015.
[10] DOYLE N F. Railway track design:a review of current practice[R]. 1980.
Effect of Wheel Flats on Wheel/rail Dynamic Interaction
in 30-ton Heavy-haul Railway
ZHANG Da-wei, WANG Kai-yun, ZHAI Wan-ming
(StateKeyLaboratoryofTractionPower,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China)
Abstract:This paper presents an investigation on the effect of wheel flats on wheel/rail dynamic interaction and the allowable limit of wheel flats in heavy-haul railway of 30-ton axle load on the basis of the vehicle-track coupled dynamics. Results show that high frequency force P1and low frequency force P2would be occur under the condition of newly formed wheel flat, whereas they would not appear instead of the maximum force Pmaxunder the condition of rounded wheel flat. Finally, the suggested allowable limit length of the wheel flats should be within 37 mm for newly formed wheel flat based on the standards of P1and P2stipulated by British Railway and within 45 mm for rounded wheel flat according to an assumed impact factor of 200% proposed by AREMA and an limit of 0.8 for the rate of wheel load reduction.
Key words:Heavy-haul railway; Wheel flats; Vehicle-track coupled dynamic; 30-ton axle load
中图分类号:U270.1+1
文献标志码:A
文章编号:1671-8755(2015)04-0015-05
作者简介:张大伟(1987—),男,博士生,研究方向为重载铁路车辆-轨道耦合系统动力学。E-mail:dwzhang1230@163.com
基金项目:国家自然科学 (51478399);国家科技支撑计划项目(2013BAG20B00)。
收稿日期:2015-07-01
