基于Halbach阵列爬壁机器人永磁轮吸附单元的设计与优化

潘柏松，张　晋，魏　凯，叶宇峰

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.浙江省特种设备研究院，浙江 杭州 310020)



基于Halbach阵列爬壁机器人永磁轮吸附单元的设计与优化

潘柏松1，张晋1，魏凯1，叶宇峰2

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.浙江省特种设备研究院，浙江 杭州 310020)

摘要：针对爬壁机器人的工作环境和要求，基于Halbach阵列理论提出了新型磁轮吸附单元的拓扑结构.通过有限元仿真研究了磁轮轭铁厚度、极对数、轴向和周向磁化单元比例等若干因素对吸附力的影响.设计了两组实验，分别测试磁轮吸附力周向变化状况和空气隙对磁轮吸附的影响.在验证分析结果准确性的基础上，基于多岛遗传优化算法对磁轮结构参数进行了全局优化分析.结果表明：优化后的磁轮吸附力与磁轮重量比与优化前相比提高了近2倍，极大地提高了磁能利用率.

关键词：环形Halbach阵列；永磁轮；遗传优化

永磁吸附是爬壁机器人众多吸附方式中比较安全可靠的一种.永磁吸附又可分为两类：一类是非接触式吸附方式，另一类是接触吸附方式.与非接触式吸附方式相比，接触吸附方式吸附力更大，适合于宽广平整的表面.磁轮作为接触吸附方式中的主要类型之一，得到广泛研究和应用.国内外学者为使爬壁机器人更好地在磁基壁面运行，研究设计了各种结构类型的磁轮[1-3].TCHE F等[4]设计了永磁吸附整体式磁轮.永磁吸附单元分别位于磁轮两侧，与磁基壁面形成磁回路，考虑到了磁轮吸附单元和磁基壁面形成磁回路对吸附力的影响.HAN S等[5]研究了磁轮中永磁单元大小和连通磁轮的引导针对吸附力的影响，表明连通磁路对吸附力的提高影响很大.KIM J等[6]进一步研究将电磁与永磁相耦合.利用电磁和永磁磁场叠加，减少了磁轮的吸附力，从而使磁轮更容易和壁面分离.TAVAKOLI M等[7]设计了一款全方向移动管道外壁爬壁机器人，此款机器人有三个磁轮构成，每一个磁轮外圈安装若干个圆形小磁块.同时研究了不同小磁块个数的影响，以及小磁块相对于壁面夹角对吸附力大小和运动平稳性的影响.

上述研究重点集中于磁轮结构和其他吸附方式耦合的研究.基于Halbach环形阵列，研究了不同磁化方向和不同尺寸的磁块组合的磁特性，并运用有限分析方法进行了优化分析与设计.

1Halbach磁环结构和理论

1.1磁轮基本结构

爬壁机器人采用磁轮接触式吸附方式(图1a)，将永磁吸附单元镶嵌在磁轮结构中，磁轮外面包裹橡胶垫层，橡胶垫层既增加了摩擦力防止磁轮打滑，又能有效保护易碎的永磁单元.

图1　爬壁打磨机器人Fig.1　Wall-climbing and grinding robot

磁轮内部结构如图1(b)所示.磁环有若干不同磁化方向的永磁单元按一定的规律排列，磁环内圈紧贴Q235材质环形轭铁.它既能更有效的按预定方向导磁，又使永磁单元的排列、安装更加方便.

1.2Halhach理论

将不同磁化方向的永磁单元按一定顺序排列，形成的Halbach阵列磁场具有明显的一边增强，一边减弱的特性，此特点恰好和磁轮的应用环境贴合.在理想的圆柱形Halbach阵列中，磁化方向的变化符合[8]式为

θm=(1±p)θ

(1)

式中：p为极对数;θm为磁化矢量和极轴的夹角;θ为某一点和极轴的夹角；“+”为磁场在内部；“-”为磁场在外部.

如图2所示，任意一点的磁化矢量在极坐标下可以表示为

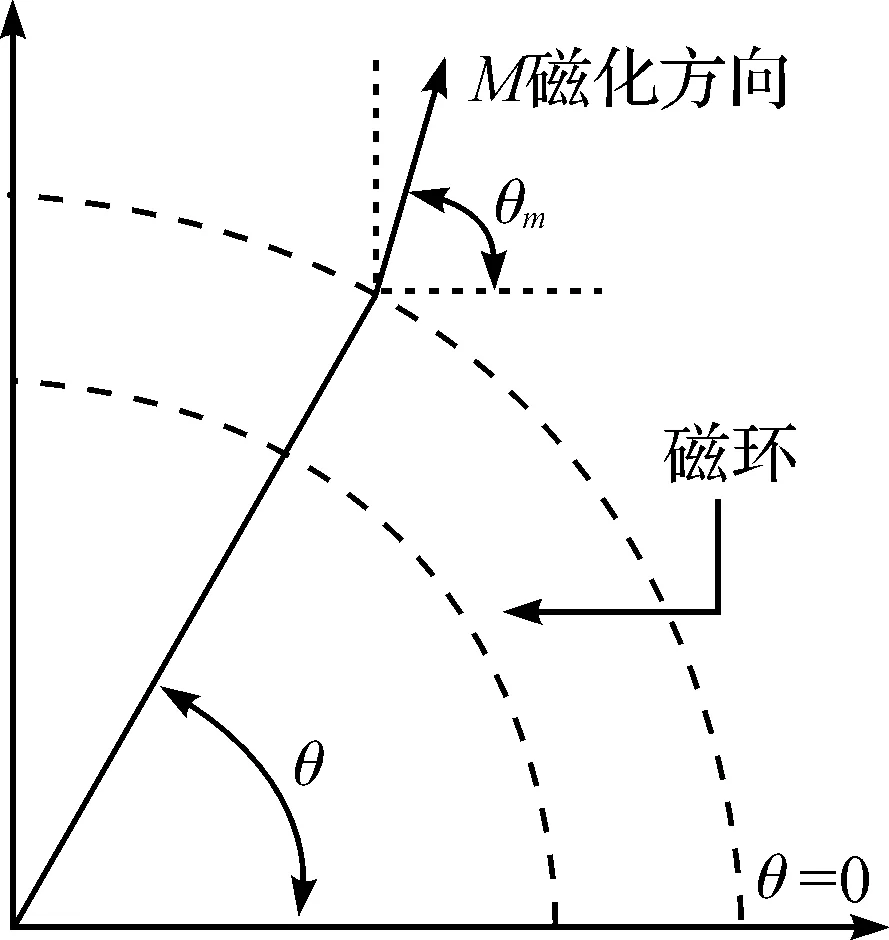
图2　θm与θ的角度关系Fig.2　Angular relationship between θm and θ

(2)

其中：er和eθ分别为径向和切向单位矢量；Mr=Mcos(p·θ)，Mθ=±Mcos(p·θ)，按式(2)的方向磁化方而成的切线方向的磁分量M相互叠加即形成理想的正弦磁场.

在实际的工程应用中，任意角度的充磁要求较高难以达到.为简化生产工艺并降低生产成本常采用冲磁角度90°的Halbach阵列[9]，因此现研究基于冲磁角度90°磁单元拼接而成的Halbach阵列.

2Halbach有限元分析与实验

2.1有限元分析的理论基础

在电磁力的计算中麦克斯韦(Maxwell)应力法相较于虚功位移法易于推导，应用也较为简单.同时当选取通过单元质心或单元中心的积分路径时，其计算精度和虚功位移法精度相同[10].

麦克斯韦(Maxwell)方程组在整个求解域，如永磁体、空气、软铁、导磁壁面均为各向同性相下，在直角坐标系展开，即

(3)

(4)

式(3，4)中：A为磁场强度；B为磁感应强度.结合磁场边界条件即可得到吸附力.

永磁吸附轮的磁吸附单元对壁面产生的吸附力，可通过麦克斯韦应力张力法计算得到.其原理可简单的阐述为：在各向同性且均匀介质中，应力张量T的积分在曲面S的面积分即为永磁单元的吸附合力F，即

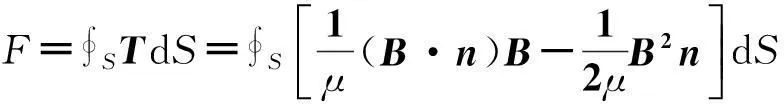
(5)

式中:S为处于各向同性且均匀介质中的闭合曲面；n为微元dS外法线单位矢量；B为磁通量密度；μ为相对磁导率.

2.2磁轮特性研究

影响稀土永磁体圆环吸附力的因数众多，除本身材质和几何尺寸外.如不同充磁角度磁单元排列方式决定磁极的个数，吸附力大小和波动变化；不同充磁角度的磁单元体积配比，轭铁厚度等对吸附力也有较大的影响.

采用的永磁材料选用钕铁硼稀土永磁材料牌号为35，其磁性能参数有生产厂家提供，参照表1.因此在仿真计算中应用的回复磁导率μrec=1.06.

表1　NdFeB-N35性能参数表

环形轭铁采用Q235材料其的B—H曲线[11]为非线性如图3所示.在低磁场时，磁通量密度随磁场强度上升迅速，后趋向平缓.

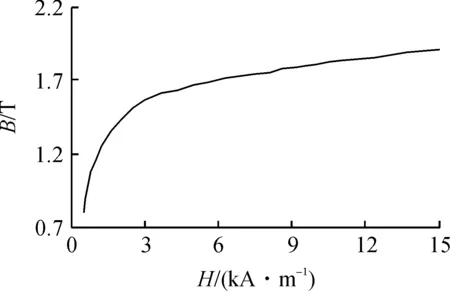
图3　Q235磁化曲线Fig.3　Q235 magnetization curve

爬壁机器人工作壁面积与厚度足够大，磁通量处于未饱和状态，因此在有限元中分析中将其看做线性材料，相对磁导率μrec=2 000.运用ANSYS求解，其几何与有限元模型如图4所示.其中参数r为磁轮半径，w为径向厚度，h为厚度，n为径向永磁单元角度，m为周向永磁单元角度.壁面厚度为3倍于永磁磁环厚度，确保了磁通量形成回路.

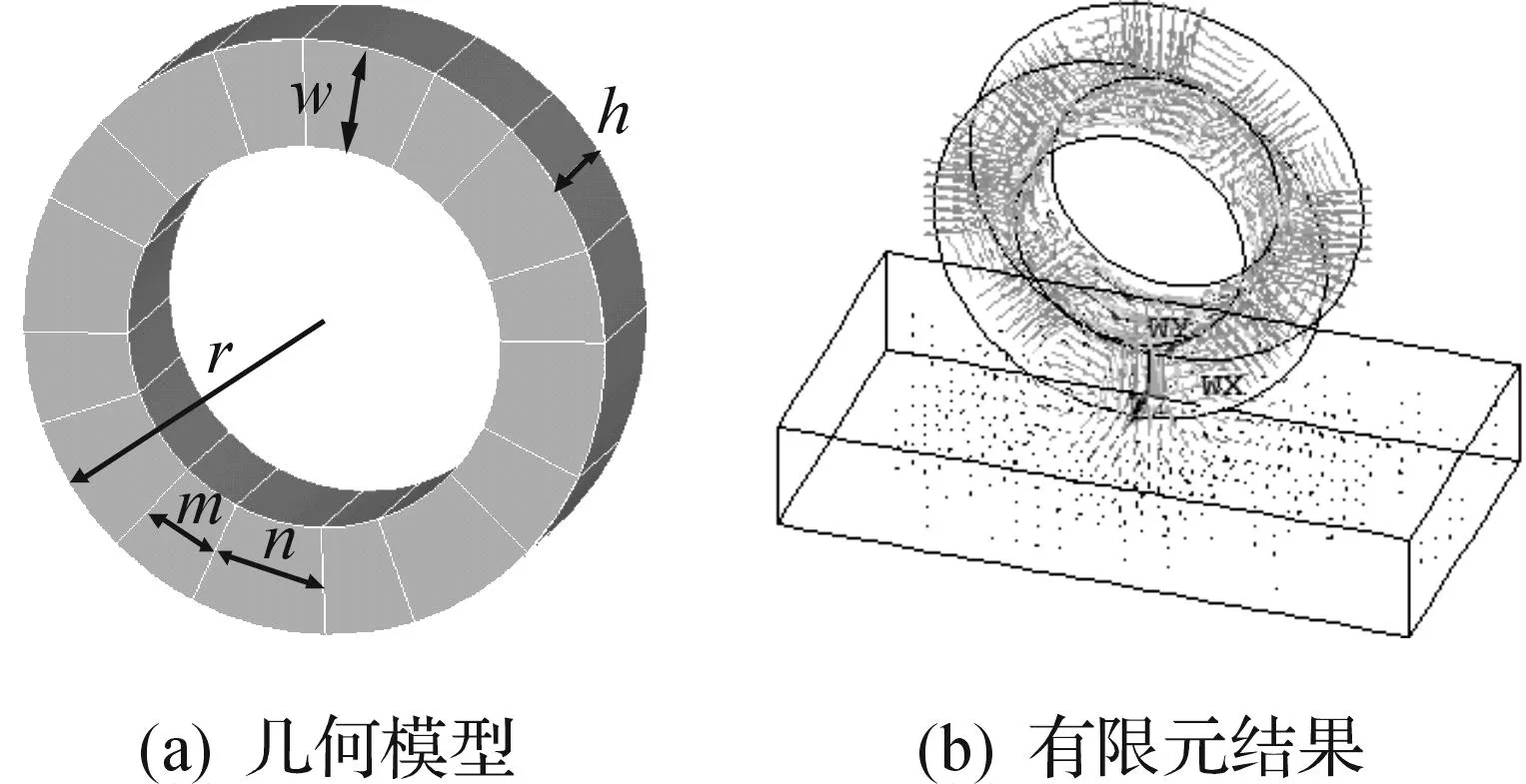
图4　有限元分析模型Fig.4　Finite element analysis model

2.2.1极对数因素

环形Halbach的排列方式变化多样，我们常把一个径向的N极永磁单元和一个环向的S极永磁单元形成的磁极称为一个极对.多极的Halbach环形中奇数极对数Halbach圆形阵列为对内加强型，偶数极对数为对外加强型.根据磁轮的应用环境，采用4，6，8，12，16偶数极对数进行分析.

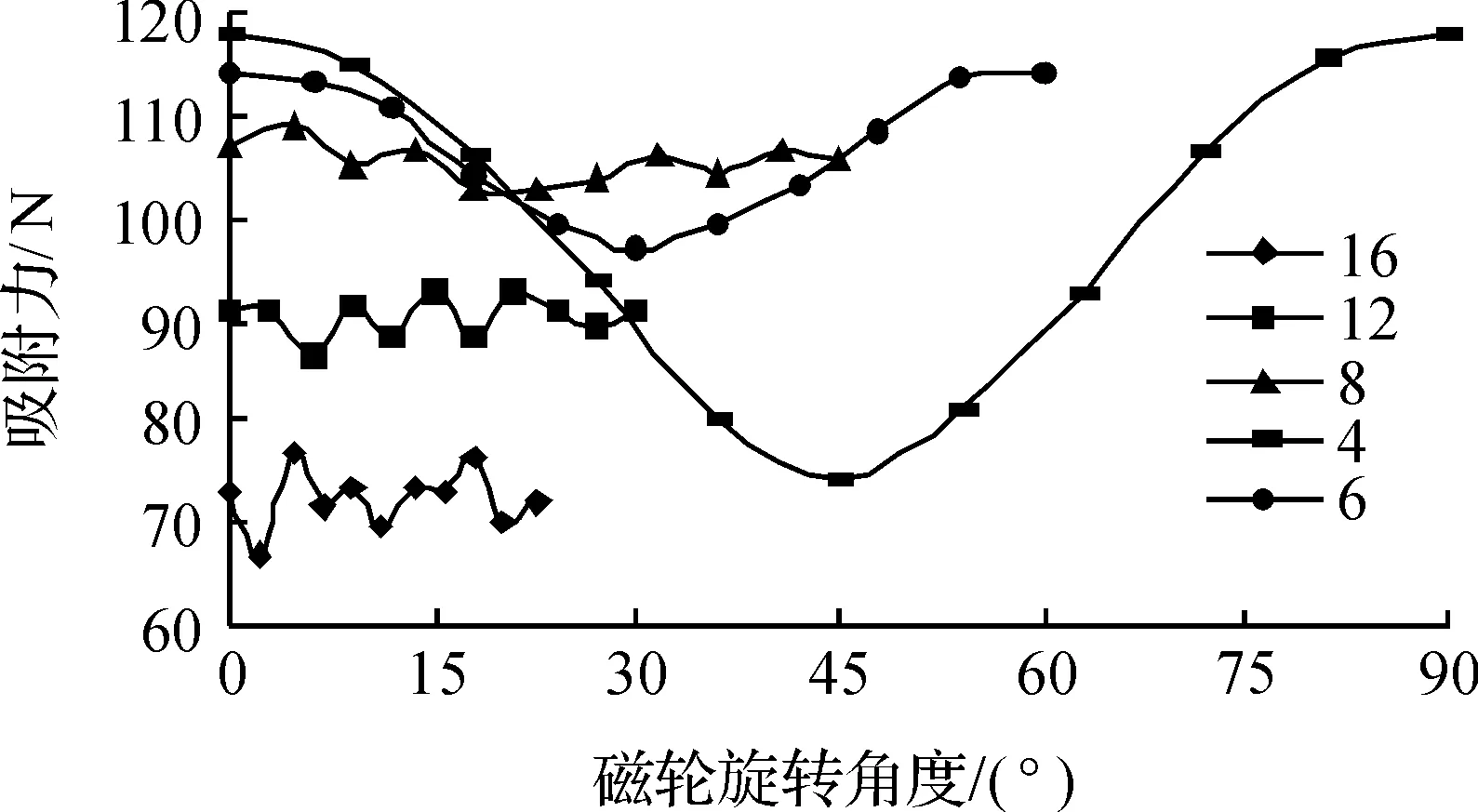
图5　不同极数吸附力周向波动Fig.5　Adsorption fluctuation of different poles in the circumferential direction

从有限元的模拟计算图5中可以得出：极对数越多，吸附力越趋于平稳，相对于极对数较少的磁轮吸附力大小峰值下降也较明显.采用8极对数磁轮，吸附力波动控制在5%以内，吸附大小较更多极的更高.

2.2.2不同体积配比

该蔬果园创始人肖健告诉记者，这里是“上风上水”处，可以尽量避免工厂废气和其他污染物排放对于蔬果造成的不利影响。

8极对数组成的磁环，研究纵向永磁单元和横向永磁单元的体积配比对吸附力的影响.为直观的反应两者的大小引入系数k值，即

(6)

式中：n为径向永磁单元角度；m为周向永磁单元角度.从有限元的仿真中，得到吸附力在k=0.6左右，磁轮吸附力将达到峰值.

2.2.3轭铁厚度

影响磁吸附力的另一个重要因素为轭铁的厚度，轭铁越厚磁漏越小，但磁轮的体积和重量也会相应的增大.从有限元的仿真模拟可以得到：吸附力先是下降，后继续上升，当环形磁轭厚度升到2 mm左右维持稳定.这现象由于轭铁的相对磁导率远高于空气，当轭铁厚度较小时出现磁饱和现象.当轭铁厚度增加，磁饱和现象消除，吸附力维持稳定.

2.3实验验证

为了验证有限元计算结果的正确性，设计了如图6的实验装置.利用万能拉压试验机传感器，测试磁轮单元的吸附力和壁面距离的关系，以及旋转角度对吸附力的影响.测试装置为铝制材料，导磁率和空气几乎一致，对结果没有影响.

图6　吸附力测试实验装置Fig.6　Measuring adsorption experimental apparatus

为了对比Halbach阵列的吸附力效果.设对向充磁磁单元为对照试样组.如7图所示.

图7　磁环结构Fig.7　Halbach magnet cylinder structure

从图8,9中可以得出：稀土永磁永磁单元吸附力对吸附距离敏感，随两者的距离增加，吸附力成指数剧烈下降.Halbach阵列相比较于普通对向极磁环，吸附距离对其影响较弱，同时吸附力增加一倍.

在磁通密度上，Halbach阵列相比较于对向充磁阵列多41%[12]，同时吸附力影响因素公式[13]为

F∝B2·S

(7)

式中：B为空气隙的磁通密度；S为吸附面截面积.

式(7)表明吸附力正比于磁通量平方.这一结论与吸附力增加一倍相吻合，很好的验证了仿真与试样的准确性.但由于加工钕铁盆稀土磁单元的加工误差和在永磁单元易碎表面脱落等原因，存在着误差，实验和仿真值误差在8%.吸附力随角度的波动在5%以内波动，认为波动较小.

图8　吸附力随距离的变化Fig.8　Magnetic wheel’s adsorption force of varies with distance

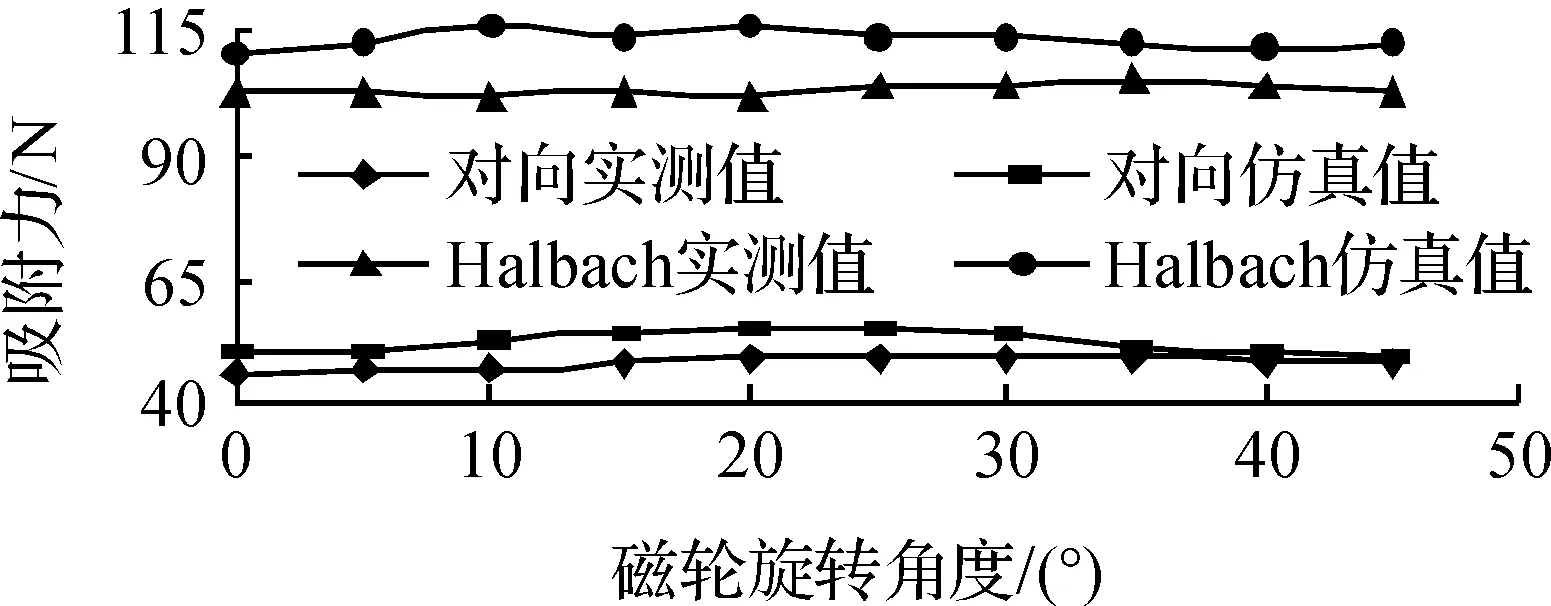
图9　旋转角度对吸附力的影响Fig.9　Influence on the adsorption force rotation angle

3结构优化设计

3.1优化参数和目标

为保证爬壁机器人在安全的吸附力下，使磁轮结构尽量紧凑，减少爬壁机器人的体积和质量，对磁轮几何尺寸进一步优化.

定义磁吸附力和磁轮重量比[14]为

(8)

式中：Fm为在一定空气隙下的磁轮吸附力；δ为磁轮与壁面之间的空气隙宽度；G为磁轮自重.

基于2.2分析可进一步优化的设计变量如下，磁轮半径r，磁轮径向宽度w，磁轮厚度h，及参数k值，其在可行域Ω变化.则优化问题表达为

3.2优化过程与结果分析

运用优化软件ISIGHT调用ANSYS-APDL文件进行批处理.磁轮结构的优化是非线性优化问题，需在几个局部最优解或较优解中寻找全局最优解.采用多岛遗传算法(Multi-IslandGA)，模拟生物体在多个岛屿环境中生命的繁衍过程，先对符合约束条件的潜在解集的种群进行遗传编码，通过模拟的逐代演化交叉、变异，搜索新产生的种群中最优解[15].设子种群规模Sub-PopulationSize为10，子种群的个数NumberofIsland为10，繁殖代数NumberofGenerations为10，经过1 000循环迭代.

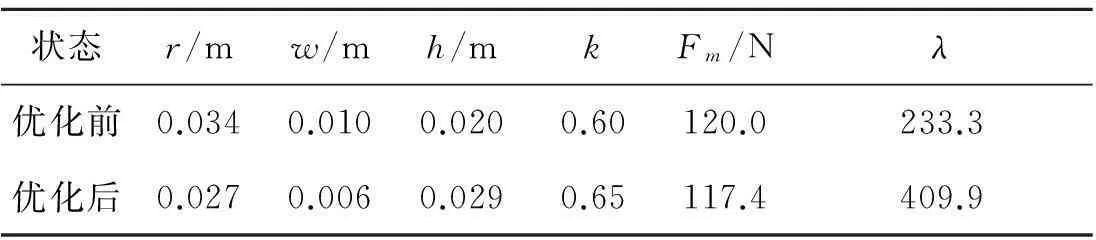
表2　几何尺寸优化前后对比

图10　优化目标λ随各参数k,w,h,r变化Fig.10　Optimization goals λ with variable k, w ,h ,r changes

从图10中得出：磁轮宽度尺寸h与吸附力大小成呈正相关趋势，但磁轮的宽度过大却对爬壁机器人运动灵活造成不良的影响.磁轮总计的体积能提供所需吸附力，k值在0.65达到最佳值，同时k对吸附力大小影响并不大.得出永磁单元的厚度在6.5 mm即能提供形成较好的波形，过大的厚度仅会增加磁轮的自重.

4结论

有限元仿真分析结合实验验证，并采用多岛遗传算法(Multi-Island GA)优化，得到了一种永磁轮新型拓扑结构.磁吸附单元优化后，最大吸附力与吸附单元重量比λ可达409.9.在相同体积质量下，其吸附力为普通磁轮的2倍，较大的提高了磁能利用率，为爬壁机器人结构设计提供依据.

参考文献：

[1]IEEE Robotics and Automation Society. 2013 44th international symposium on robotics (ISR)[C]. Seoul:IEEE,2013:1-4.

[2]SCHMIDT D, BERNS K. Climbing robots for maintenance and inspections of vertical structures-a survey of design aspects and technologies[J]. Robotics and Autonomous Systems,2013,61(12):1288-1305.

[3]OKAMOTO J J, GRASSI J V, AMARAL P F S, et al. Development of an autonomous robot for gas storage spheres inspection[J]. Journal of Intelligent & Robotic Systems，2012,66(1/2):23-35.

[5]HAN S, KIM J, YI H. A novel design of permanent magnet wheel with induction pin for mobile robot[J]. International Journal of Precision Engineering and Manufacturing，2009,10(4):143-146.

[6]KIM J, PARK S, KIM J, et al. Design and experimental implementation of easily detachable permanent magnet reluctance wheel for wall-climbing mobile robot[J]. Journal of Magnetics，2010,15(3):128-131.

[7]TAVAKOLI M, VIEGAS C, MARQUES L, et al. Omniclimbers: omni-directional magnetic wheeled climbing robots for inspection of ferromagnetic structures[J]. Robotics and Autonomous Systems,2013,61(9):997-1007.

[8]IEEE Power Eletronics Society. 2000 the third power electronics and motion control conference[C]. Beijing:IEEE,2000：903-908.

[9]李耕,乔鸣忠,梁京辉,等.Halbach结构永磁电机优化设计[J].电机与控制应用，2012,39(1):6-10.

[10]阎秀恪,谢德馨,高彰燮,等.电磁力有限元分析中麦克斯韦应力法的积分路径选取的研究[J].电工技术学报，2003,18(5):32-36

[11]李泉风.电磁场数值计算与电磁铁设计[M].北京：清华大学出版社,2002.

[12]周赣,黄学良,周勤博,等.Halbach型永磁阵列的应用综述[J].微特电机,2008,8(1):52-55.

[13]陈勇,王昌明,包建东.新型爬壁机器人磁吸附单元优化设计[J].兵工学报,2012,33(12):1539-1544.

[14]桂仲成,陈强,孙振国,等.爬壁机器人永磁吸附装置的优化设计[J].电工技术学报,2006,21(11):40-46.

[15]杜时贵,万颖君,彭卫.改进的遗传算法在结构优化设计中的应用[J].浙江工业大学学报,2004,32(2):174-177.

(责任编辑：刘岩)

The optimization of a novel permanent-magnetic wheel adsorption unit

for wall-climbing robot based on Halbach array

PAN Baisong1, ZHANG Jin1, WEI Kai1,YE Yufeng2

(1.College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China；

2. Zhejiang Province Special Equipment Inspection and Research Institute, Hangzhou 310020, China)

Abstract:Under the wall-climbing robot’s working environment and design requirements, a new magnetic wheel adsorption topology unit is put forward based on the Halbach array theory. We studied the thickness of the magnetic yoke round, the number of poles, the proportion of unit on the axial and circumferential magnetization on the adsorption force by the finite element simulation. Two control experiments are designed to study the circumferential magnetic wheel impact on magnetic wheel adsorption force, effect of the air gap. After verifying the accuracy of the results, structure of magnetic wheels global optimization parameters were analyzed by using a multi-island genetic algorithm. The result illustrates the ratio of adsorption and quality of the optimized structure increased nearly 2 times of that of before, which greatly improves the utilization of the magnetic energy.

Keywords:Halbach magnet cylinder; permanent magnet wheel; genetic optimization

文章编号：1006-4303(2015)04-0393-05

中图分类号：TP24

文献标志码：A

作者简介：潘柏松(1968—)，男，浙江温岭人，教授，主要从事智能制造装备技术、设计理论与方法及可靠性设计技术，E-mail：panbsz@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(51475425)；浙江省自然科学基金资助项目(20140120)；浙江省质量技术监督局重大科研项目(20140120)；浙江省大学生科技创新新苗人才计划项目(2014R403081)

收稿日期：2014-12-31