基于振型的构件位移分解及规律研究
2016-01-20吴泽玉,王东炜,汪志昊
基于振型的构件位移分解及规律研究
吴泽玉1, 王东炜2, 汪志昊3
(1.北京工业大学 建工学院,北京 100124; 2.郑州大学 土木工程学院,河南 郑州 450001; 3.华北水利水电大学 土木与交通学院,河南 郑州 450000)
摘要:为了清楚分析结构的荷载效应,可将位移向振型方向投影,计算位移在各个振型中所占比重.增加对结构变形有利振型位移所占比例,降低对结构变形不利振型位移所占比例.提出位移展开所需振型量确定方法和位移和应变、应力及内力用振型展开的相关表达式.通过对普通梁、适中柱及深受弯构件和短柱位移展开,得到梁柱荷载效应的一般规律.
关键词:振型;位移;振型方向系数;构件;概念设计
收稿日期:2015-03-30;
修订日期:2015-05-28
基金项目:国家自然科学基金项目资助项目(50978232);河南教育厅项目资助(14B560029)
作者简介:吴泽玉(1976—),男,河南固始人,北京工业大学讲师,博士,主要从事复杂结构体系选型与振动控制研究,E-mail: 13598437507@163.com.
文章编号:1671-6833(2015)05-0068-05
中图分类号:TU311.1
文献标志码:A
doi:10.3969/j.issn.1671-6833.2015.05.015
Abstract:In order to clarify the external load effect on structure, the displacement can be decomposed on the mode and calculated the proportion of the each mode. The advantage mode displacement can be increased and disadvantage mode displacement can be decreased. To meet the engineering safety requirements, the mode number of displacement expansion is determined and stress equation, strain equation and relevant internal force equation can be derived on mode coordinate system. Through the load effect of beam and column, some valuable laws were obtained.
0引言
振型通常用来研究结构损伤检测和动力性能[1-5],鲜有用来指导结构概念设计和构造设计.王东炜等人率先提出利用振型研究结构整体力学性能,取得了很好的工程应用经验[6-7].为了清楚了解构件在外界荷载作用下的效应机理,更好地指导结构设计,可将位移向振型方向投影.增加对结构变形有利的振型位移值,减少对结构变形不利的振型位移值.在结构概念设计阶段,对结构整体受力性能进行宏观控制,使对结构概念设计有了量化措施.振型描述了刚度和质量在整个结构体上的分布,表征二者的相对比值关系,为二者的相对比值关系在空间位置上的分布情况.同时,振型也反映了结构在外界荷载作用下最易发生变形的先后顺序.外力作用对结构都会产生效应,通常以位移的形式表现出来.结构振型是位移的广义完备正交基,通过位移在振型坐标基上的展开,可清楚了解外力的作用效应以及这种效应在各振型中所占的比例,特别是容易引起结构脆性破坏的剪切效应和扭转效应.故在结构设计时,提高对结构变形有利的振型所占的比重,减少对结构变形不利的振型所占的比重,用来指导结构概念设计和构造设计.
1位移、应变和应力振型展开
振型是结构位移的完备正交基,任何位移都能以振型为坐标基展开,表示为振型和振型幅值乘积的形式,如式(1)所示[8]
D=a1φ1+a2φ2+…+anφn,
(1)
式中:D表示位移向量;φn表示结构的振型;an表示位移展开在各振型中的振幅.利用振型的正交性,式(1)中各振型幅值系数

(2)

{ε}=[L]{D} ,
(3)
式中:{ε}为应变矩阵;[L]为微分算子矩阵.应力与应变的关系式为
{σ}=[K]{ε} ,
(4)
式中:{σ}为应力矩阵;[K]为刚度矩阵.
{εn}=anφn[L]{D},
(5)
{σn}=[K]{ε}=anφn[K][L]{D}.
(6)
从式(2)~(6)可以看出,只要构件位移已知,就可以求出相应的应变和应力在振型上的投影值,对应力在面内或体积内积分,可求出相应的内力值.位移在振型上投影的幅度值an反映了外界荷载对各振型的作用效应,因此对an分析就能显示荷载效应在振型分配大小.
2满足精度要求的振型数量
计算位移展开所需振型数可由范数确定[10-12].设需展开的位移向量为{D},假定前M阶振型展开的位移量为{Ds},展开位移与实际位移之间的误差为
{E}={D}-{Ds} ,
(7)
对式(7)的差值位移向量,可由3种方法确定所需振型数量.
(1) 均方法

(8)
式中:Di为位移向量{D}中的分量;Dsi为位移向量{Ds}中的分量.当‖E‖2值满足计算精度时,所取的振型阶数M即为所需振型量.
(2) 最大位移法
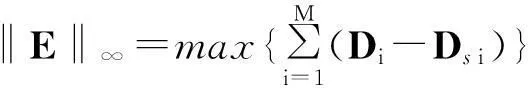
(9)
由公式可知,展开振型阶次越高,任意自由度位移误差逐渐收敛展开位移量.
【国际原子能机构网站2018年9月14日报道】 2018年9月,国际原子能机构(IAEA)发布《2018年气候变化与核电》报告,并在报告中表示,核电可以在为全球经济发展提供所需电力的同时,为实现气候变化目标做出重要贡献。该报告是2016年版报告的更新版,在其中加入了有关能源生产与气候变化之间联系的最新科学信息和分析结果。原子能机构希望这份报告能为参与《联合国气候变化框架公约》等论坛活动的决策者提供有用信息。
(3) 百分比法

(10)
3适中柱和普通梁位移量在振型坐标基上的投影
3.1适中柱位移在振型上的投影分析
某柱横截面为0.8m×0.8m高为6m,横截面方向为x和y坐标,柱高为z向.假定反弯点在柱中点,取一半柱高分析,约束形式为上端自由下端固定.柱的剪跨比为:λ=3.75>2,为适中柱[13].结构自由端结点图如图1所示.水平和竖向力均为1 000kN,分析位移在振型上的投影规律.水平力分别作用于结点309、373、372和结点25时,位移在前10阶振型上的位移投影系数.水平力位移展开系数和双向偏心受压和单向偏心受压位移展开系数如表1和表2所示.
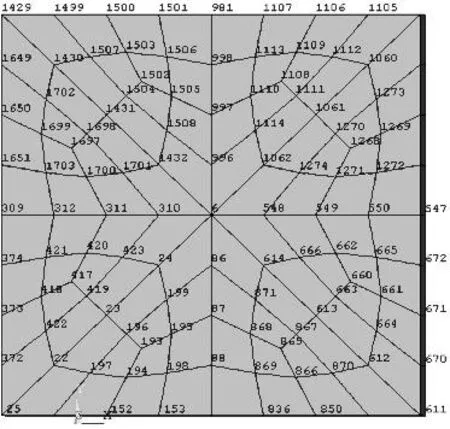
图1适中柱自由端结点图
Fig.1Free end node of moderate column

图2普通梁跨中结点图
Fig.2Middle span node of moderate beam
3.2普通梁位移在振型上的投影分析
某梁横截面为0.6 m×0.8 m,跨度为8 m,假定梁两端固定.梁的跨高比为:l0/h=10>5,为普通梁.构件的跨中结点图如图2所示.梁跨中受竖向力为集中力1 000 kN,作用于梁的跨中.分析荷载在梁横截面上移动时,位移在振型上的投影规律.普通梁在横向荷载作用下位移在各振型上展开比例如表2所示.
4短柱和深梁在振型坐标基上的投影
4.1短柱位移在振型上的投影分析
某柱横截面为0.8 m×0.8 m,高为2.4 m,假定反弯点在柱高中点,约束形式为上端自由下端固定.柱的剪跨比为:λ=1.5<2,为短柱.结构的自由端结点图如图3所示.水平和竖向力均为1 000 kN,分析位移在振型上的投影规律.水平力位移展开系数和双向偏压展开系数如表3所示.单向偏压位移展开系数如表4所示.
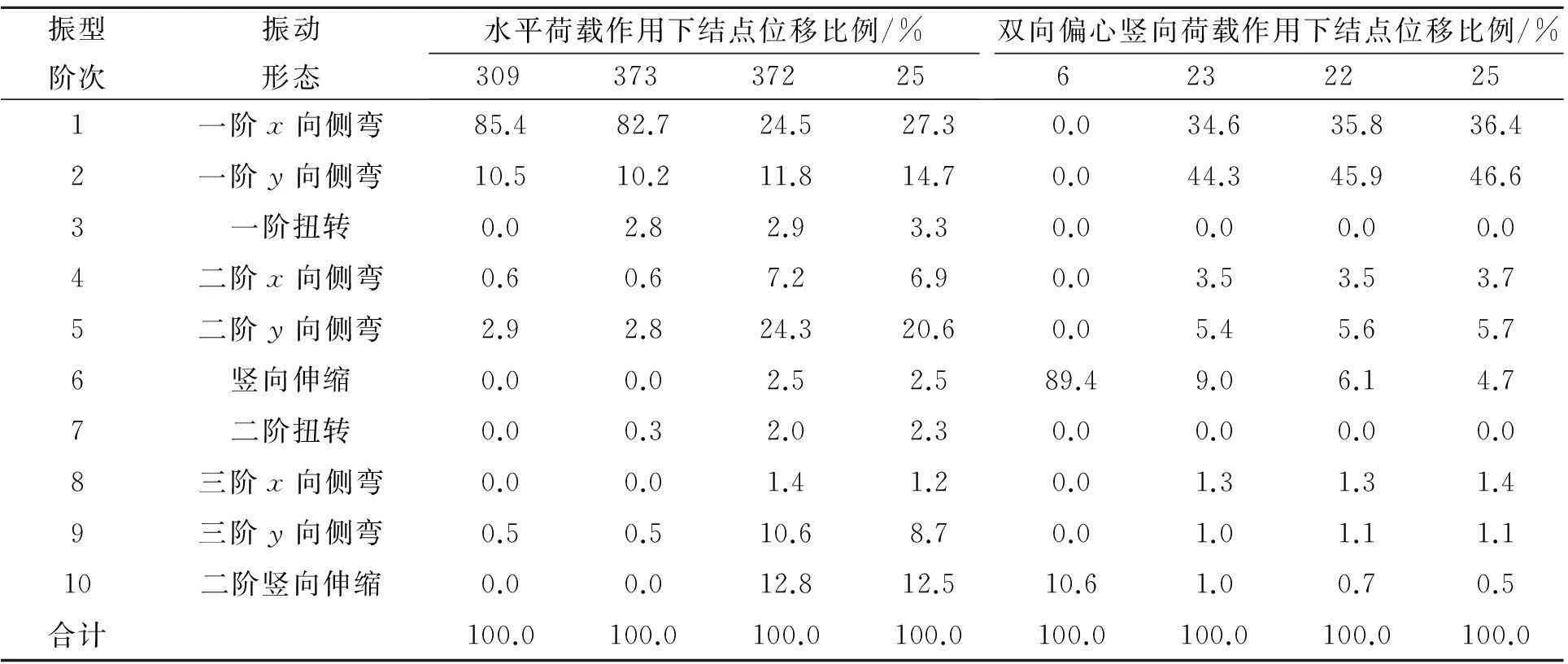
表1 水平荷载作用下和双向偏心竖向荷载作用下结点位移在振型上展开比例
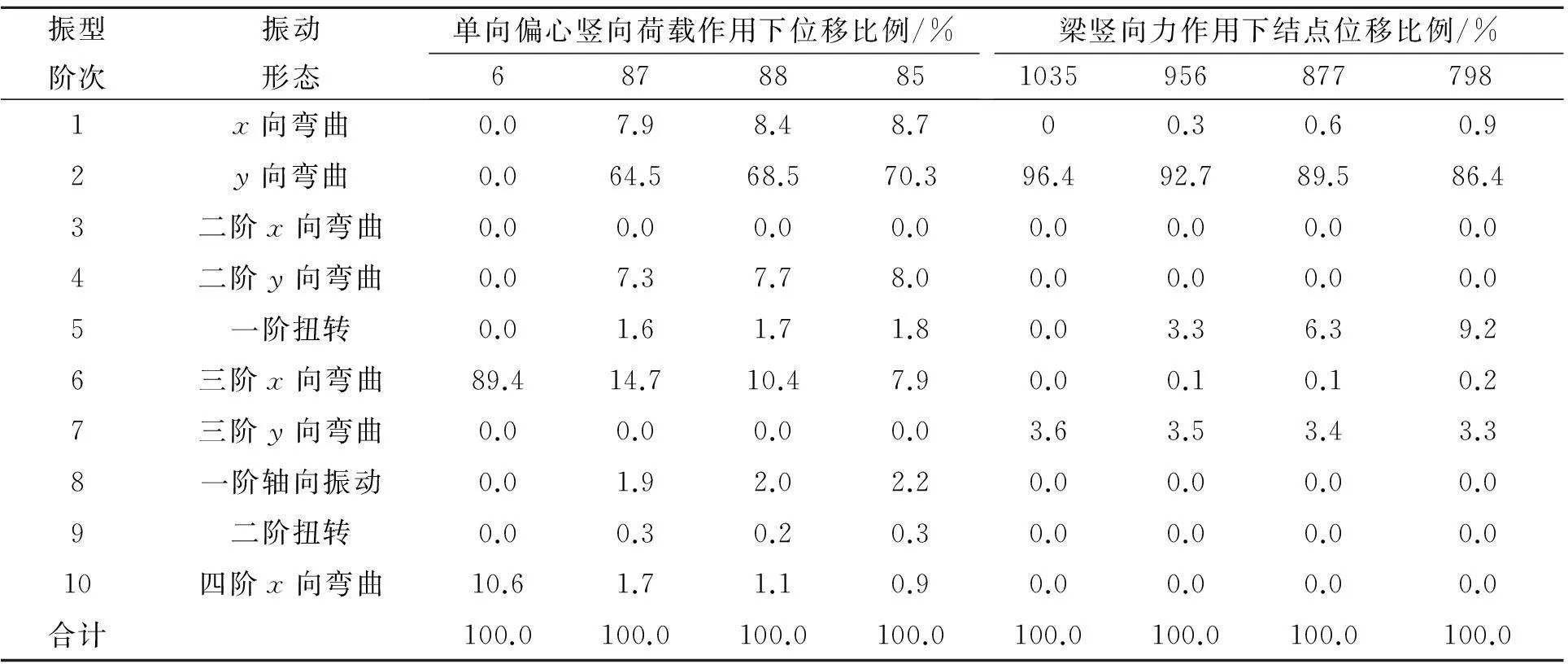
表2 柱单向偏心竖向荷载作用下和梁竖向力作用下结点位移在振型上展开比例
4.2深受弯构件位移在振型上的投影分析
某梁横截面为0.6 m×0.8 m,跨度为3.2 m,假定梁两端固定.梁的跨高比为:l0/h=4<5,为深受弯构件.构件的结点图如图4所示.梁跨中受竖向力为集中力,大小等于1 000 kN,作用于梁的跨中,分析荷载在梁横截面上移动时,位移在振型上的投影规律.深梁在横向荷载作用下位移在各振型上展开比例如表4所示.
5结论
对由梁柱组成的结构体系来说,基于振型的位移展开可清楚了解构件的变形性态,尽可能避免短柱和深受弯构件的出现,实在无法避免时,要提高构件的抗剪和抗扭能力.通过位移在振型上的展开可以指导结构概念设计和构造设计.

图3短柱自由端结点图
Fig.3Free end node of short column

图4深受弯梁跨中结点图
Fig.4Middle span node of short beam
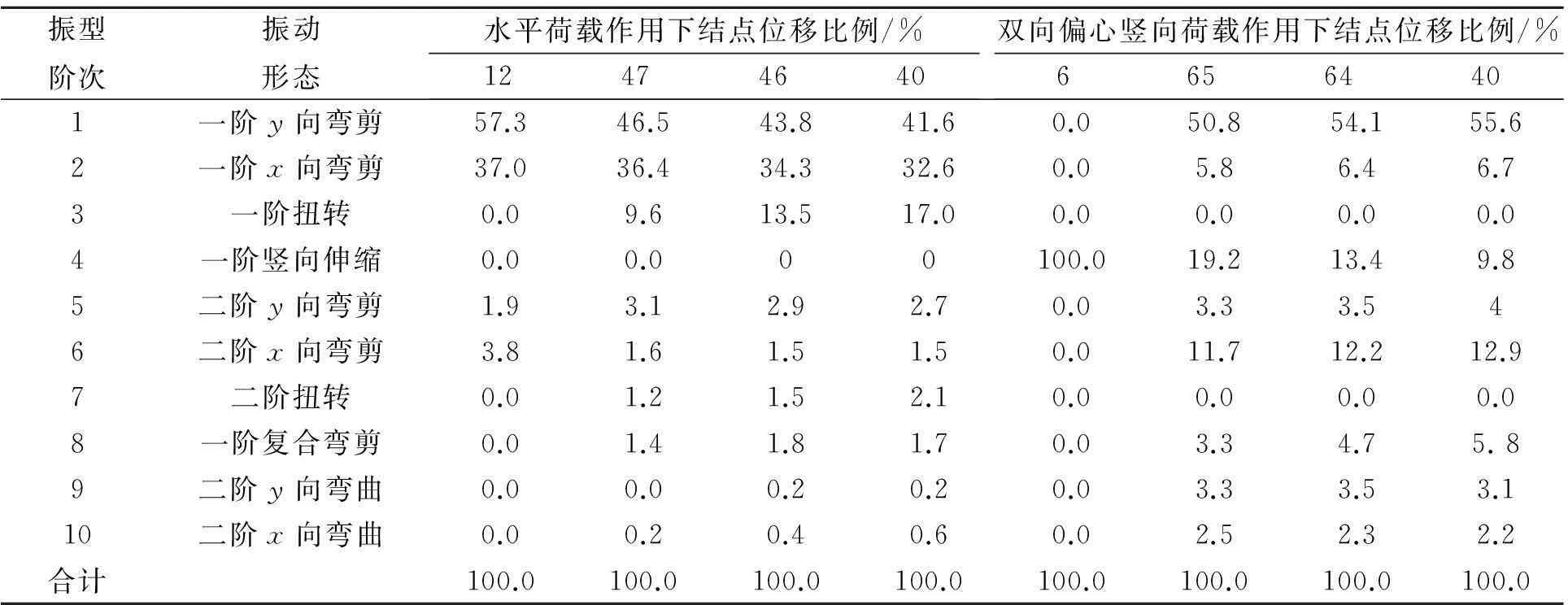
表3 水平荷载作用下结点位移在振型上展开比例
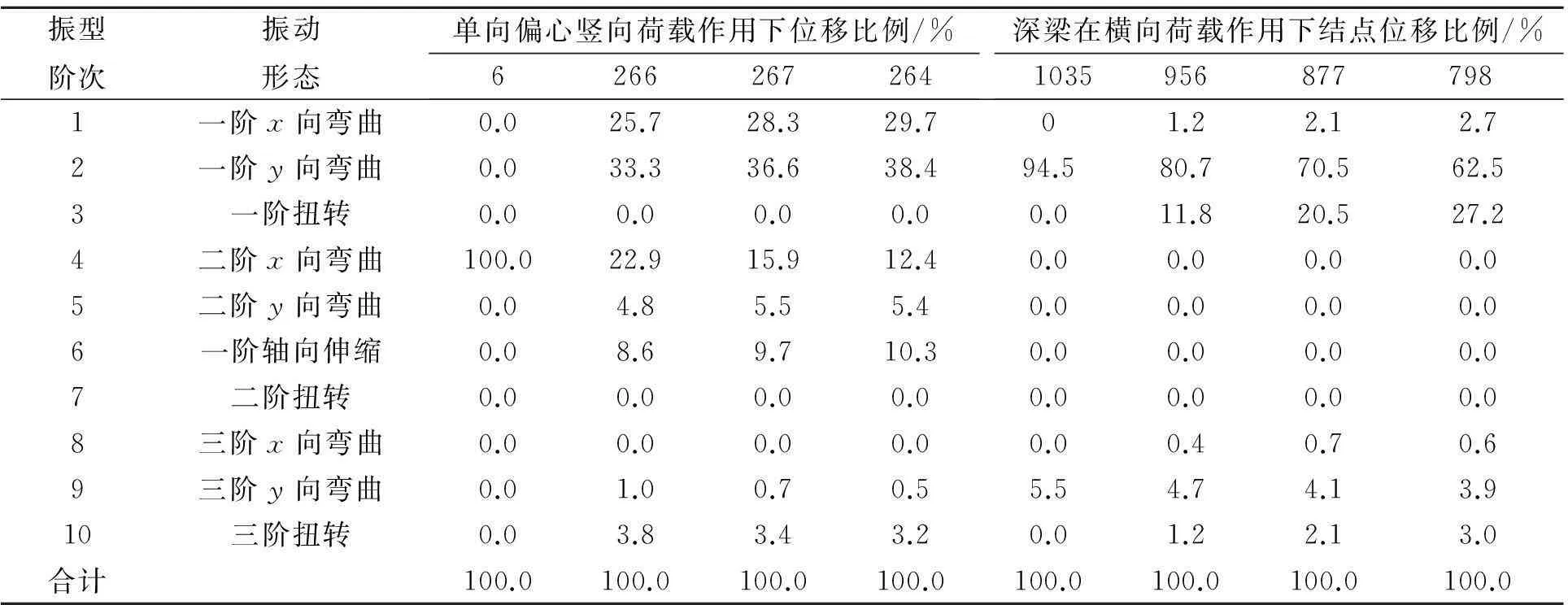
表4 单向偏心竖向荷载作用下和深梁在横向荷载作用下结点位移在振型上展开比例
参考文献:
[1]WANG Xi-ping, JAMES P W, ROBERT J R, et al.Nondestructive assessment of timber bridges using a vibration-based method[C]. Structure2005, 2005: 1~12.
[2]HWANG Jin-hung, WU Chia-pin, CHOU Jui-te. Motion characteristics of compacted earth dams under small earthquake excitation in Taiwan[J]. Geotechnical Earthquake and Engineering and Soil Dynamics, 2008, 5(2): 1~12.
[3]TRAVIS T, MARVIN W H, PAUl J B. Structural health monitoring of the Cherry Hill bridge[C]. Structure2006, 2006: 1~8.
[4]MICHELE D, ANTONINO M. Reconstruction method for damage detection in beams based on natural frequency and antiresonant frequency measurements[J]. Engineering Mechanics, 2010, 136(3): 329~344.
[5]ROBERT B, CHARLES S, SOOYONG P, et al.Modal property changes of a seismically damaged concrete bridge[J]. Bridge Engineering, 2010, 10(4): 415~428.
[6]季三荣,王东炜,赵骞. 基于模态分析的钢管脚手架平面支撑刚度研究[J]. 郑州大学学报:工学版,2010,31(4):31~35.
[7]王东炜,张奇伟,王用中.基于模态分析的鄄城黄河公路大桥优化设计[J]. 郑州大学学报:工学版,2010,31(6):1~5.
[8]RAY C, JOSEPH P. Dynamics of structures[M].Berkeley ,California,USA, Computers and Structures, Inc, 1995:101~105.
[9]Elsevier(Singapore) Pte Ltd. Finite element method[M].2008: 120~125.
[10]庄茁.连续体和结构的非线性有限元[M].北京: 清华大学出版社,2008.
[11]史荣昌,魏丰.矩阵分析[M].北京: 北京理工大学出版社,2010.
[12]李清扬,王能超,易大义. 数值分析[M].北京: 清华大学出版社,1986.
[13]中华人民共和国住房与城乡建设部.GB 50010—2010,混凝土结构设计规范[S]. 北京:中国建筑工业出版社,2010.
Research on Mode-based Displacement Expansion of
Stuctural Component and Common Rules
WU Ze-yu1, WANG Dong-wei2, WANG Zhi-hao3
(1.College of Architecture of Civil Engineering, Beijing University of Technology, Beijing 100124, China; 2.College of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China; 3.School of Civil Engineering and Communication, North China University of Water Resources and Electric Power, Zhengzhou 450000, China)
Key words: mode; displacement; mode directional coefficient; structural member; concept design
