基于响应面方法的结构非概率可靠性分析
2016-01-20陈江义,文尉超,王迎佳
基于响应面方法的结构非概率可靠性分析
陈江义, 文尉超, 王迎佳
(郑州大学 机械工程学院,河南 郑州 450001)
摘要:响应面方法可以用来建立工程结构极限状态函数的显式数学表达式,而椭球模型和区间模型则是计算结构非概率可靠性指标的两种基本模型.笔者基于响应面方法,用二次多项式近似拟合结构的极限状态函数,然后分别采用椭球模型和区间模型对结构的非概率可靠性指标进行计算,最后以悬臂梁作为算例,对不同模型计算出的可靠性指标进行了比较.结果表明:在对结构进行非概率可靠性设计时,使用区间模型要比椭球模型更安全.
关键词:非概率可靠性;椭球模型;区间模型;响应面方法
收稿日期:2015-04-29;
修订日期:2015-07-28
基金项目:河南省科技攻关重点资助项目(132102210107);河南省教育厅科学研究重点项目(13A460719)
作者简介:陈江义(1974—),男,湖北仙桃人,郑州大学副教授,博士,主要从事结构动力学,CAD技术方面的研究,E-mail:cjy1974@zzu.edu.cn.
文章编号:1671-6833(2015)05-0121-04
中图分类号:TB114.3
文献标志码:A
doi:10.3969/j.issn.1671-6833.2015.05.026
Abstract:Response surface method (RSM) is often employed to construct the explicit mathematical expression of the limit state function of engineering structure. And the non-probabilistic reliability of engineering structure can be evaluated by using two basic models which are ellipsoid model and interval model. Based on RSM, the quadratic polynomial is adopted to replace approximately the limit-state function in this paper. Then ellipsoid model and interval model are used to evaluate the non-probabilistic reliability of engineering structure. Finally, as a numerical example, the non-probabilistic reliability of a cantilever beam is analyzed and compared. The numerical result shows that interval model is safer than ellipsoid model for evaluation of the non-probabilistic reliability of structures.
0引言
在工程结构设计中,不确定因素很多,如材料属性、载荷和几何尺寸的不确定性,这些因素往往对结构的可靠性产生直接影响.基于概率的可靠性设计是处理不确定因素的有效途径之一,近几十年的研究在理论和应用上都已有充分的证明[1].概率可靠性模型需要足够的数据来描述不确定变量的概率特征,然而在工程实践中,这些数据难以获得,并且概率可靠性对随机参数的分布信息非常敏感,即模型数据的小误差可能导致结构可靠性计算出现较大的误差[2].
在工程实践中,不确定变量的概率分布虽不易确定,但其界限一般较易获得,可使用凸模型(包括超椭球模型和超立方盒模型)处理这类不确定但有界的参数.20世纪90年代Ben-haim[3]和Elisbakoff[4]提出了基于凸集模型的非概率可靠性概念,与概率可靠性强调系统可接受不确定性的概率不同,它强调系统可接受不确定性的范围.郭书祥等[5]对结构非概率可靠性方法和概率可靠性方法进行了比较,验证了当掌握的信息数据较少时,非概率可靠性方法的适用性.亢战等[6]建立了基于凸模型的非概率理论体系,用椭球模型计算了非概率可靠性指标,并用于优化.郭书祥等[7]建立了基于区间模型的非概率可靠性理论体系以及对非概率可靠性指标的求解方法.非概率可靠性技术已经成功地应用到一些相对简单的结构实例分析中,但对于解决较复杂的工程问题仍具有一定的挑战性,这些复杂结构的功能函数一般不可以用显式函数来表达,故其可靠性分析比较困难.响应面方法[8]能够拟合出一个基于显式函数的功能函数模型,从而可以完成非概率可靠性分析.
笔者运用响应面方法构建极限状态方程,基于椭球模型和区间模型分别计算结构的可靠性指标并进行比较,最后以悬臂梁作为算例验证笔者提出方法的正确性.
1非概率可靠性指标
1.1椭球模型
在结构可靠性分析中,结构的极限状态方程一般由功能函数或极限状态函数描述
g(X)=0,
(1)
式中:X=[x1,x2,…,xn]∈Rn表示所有具有不确定性的设计变量.极限状态方程将设计空间划分成可靠性区间(g(X)>0)和失效区间(g(X)<0)两部分.不确定变量X的界定可用以下椭球模型[9]确定
(X-Xc)G(X-Xc)≤1,
式中:Xc为X的均值;矩阵G是一个表示椭球模型特征的正定矩阵,用来确定椭球体的主轴方向和大小.
为便于计算可靠性指标,首先将不确定变量X中各元素归一化为
(3)
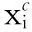
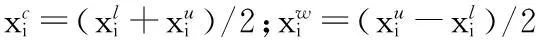
(4)
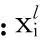
基于标准变换,转化为在U空间上的等效椭球模型
UTWU≤1,
(5)
式中:W表示在U空间上的特征矩阵.
对W进行特征值分解
ΦTWΦ=Λ,ΦTΦ=I,
(6)
式中:Φ是由特征向量组成的正交化矩阵;Λ是由矩阵W的特征值组成的对角矩阵;I是单位矩阵,引入向量δ
δ=Λ1/2ΦTU.
(7)
将式(7)带入式(2),椭球模型转化为
δ∈Ωδ={δ|δTδ≤1}.
(8)
同样在δ空间内,可以获得转化的极限状态方程
g(δ)=0.
(9)
1.2区间模型
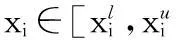
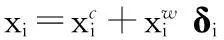
(10)
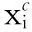
M=g(X)=G(δ),
(11)
式中:δ={δ1,…,δn}.
1.3非概率可靠性指标
为便于直观了解非概率可靠性指标,图1展示了二维情形下椭球模型和区间模型非概率可靠性指标的几何意义.图中曲线为极限状态曲线,曲线两侧分别为失效区域和安全区域.图(a)中单位圆和图(b)中正方形为不确定设计变量对应的标准化凸域,可靠性指标β定义为从原点到极限状态曲线的最短距离,只不过椭球模型按二范数来度量距离,而区间模型按无穷范数来度量距离.因此基于椭球模型的可靠性指标为
β=min‖δ‖,
s.t.g(δ)=0,
(12)
式中:‖·‖代表向量的二范数.基于区间模型的可靠性指标为
β=min(‖δ‖∞),
s.t.G(δ)=0,
(13)
式中:‖δ‖∞表示无穷范数.这样非概率可靠性指标β的求解转化为式(12)和式(13)的优化问题.
从图1还可以看出,若β≤1,失效区与不确定变量凸域有交集,所以结构可能处于失效状态;当β>1,表示结构完全可靠.β值越大,结构能容许的不确定变量变差程度越大,结构越可靠.
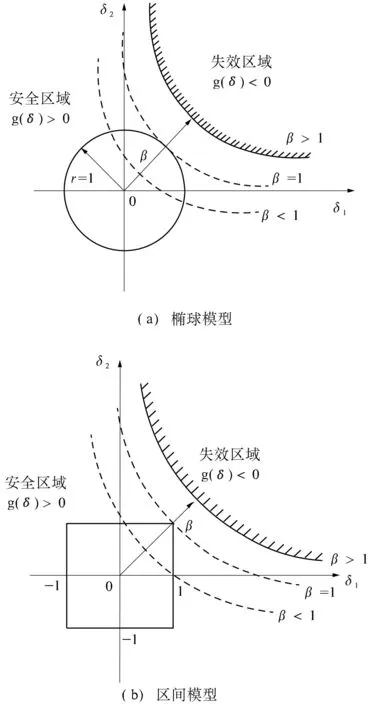
图1基于两种模型的非概率可靠性指标
Fig.1Non-probabilisticreliabilityindexbasedontwo
differentmodels(a)Ellipsoidmodel(b)Intervalmodel
2响应面方法
响应面方法是一种数学建模方法,其基本思想是通过一系列的试验设计点拟合出一个显式函数,用来近似代替复杂的物理模型,在可靠性分析中可以用来构造功能函数.
响应面的数学表达式在能描述真实功能函数的前提下应尽可能简单,一般可选用二次多项式进行回归分析
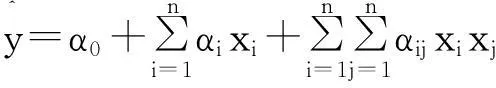
(14)
式中:α0、αi、αij为待定因子,通常用最小二乘法确定.通过变量代换将其化为形式上的线性函数,便于下面的推导,得到统一的形式
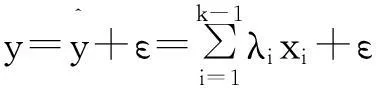
(15)
式中:λi为待定系数.
通过试验设计,得到m(m≥k)个样本点,将其带入式(15)中,得到一系列的数据.利用最小二乘法原理拟合所有试验数据点,可将其误差的平方和表示为
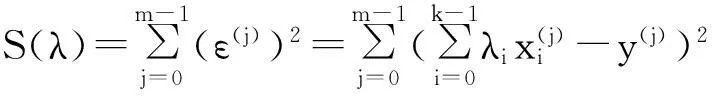
(16)
式(16)取极小值的必要条件是
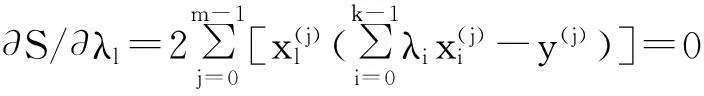
l=0,1,…,(k-1).
(17)
将这k个方程化简并整理成矩阵形式为
(Xλ-y)TX=0,
(18)
解式(18)可得
λ=(XTX)-1XTy.
(19)
将其代入式(15)中,经过变量代换得出响应面的二次多项式.
3算例及分析
以图2中的悬臂梁结构[9]为对象进行非概率可靠性分析,该结构尽管简单,但足以说明笔者提出的方法.梁的长度为L,宽度和高度分别为b和h,受水平和垂直载荷分别为Px=50 kN和Py=25 kN.极限状态方程定义为最大应力小于许用屈服强度S,
g(b,h,L)=S-σmax(b,h,L),
(20)
式中:L、b和h为不确定变量,其变化范围分别为L[900 mm,1 100 mm]、b[90 mm,110 mm]和h[180 mm,220 mm].
对于式(20)所表示的极限状态方程,可通过有限元方法获得模拟试验样本点,然后采用响应面方法将其转化为显式的二次多项式
g(b,h,L)=S-815.942+12.908b-0.420L-0.047b2+0.001 2hL.
(21)
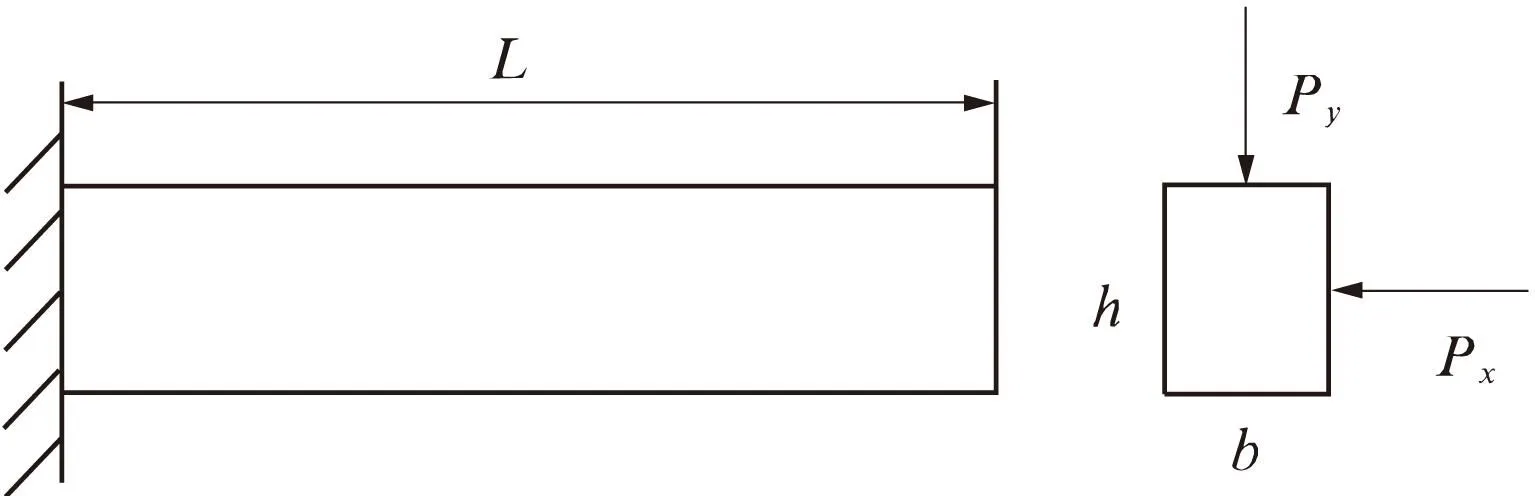
图2悬臂梁结构
Fig.2Acantileverbeam
表1为利用椭球模型和区间模型计算出的非概率可靠性指标β.为了检验响应面方法的正确性,在用上述模型计算可靠性时,分别采用有限元方法(FEM)和响应面方法(RSM).
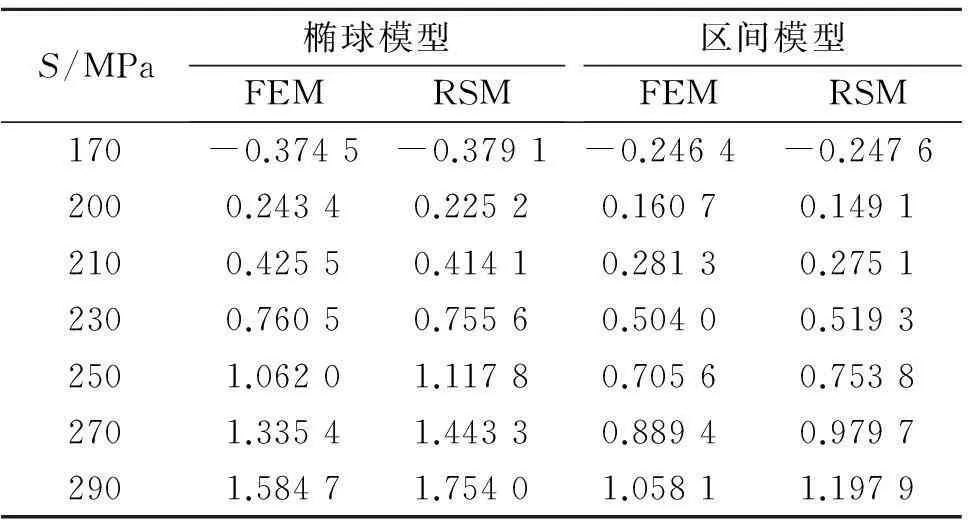
表1 悬臂梁的可靠性指标β
由表1可以得出:①对于同一种模型,利用RSM方法与FEM方法计算出的可靠性指标基本相同,尤其是在S较小的区域,说明用响应面方法构建分析模型是可行的;②在β>0区域,在同一许用屈服强度S下,基于区间模型的可靠性指标小于基于椭球模型可靠性指标,说明在进行结构非概率可靠性设计时,如果满足同一可靠性指标的要求,区间模型相对于椭球模型更安全些.
4结论
工程结构的极限状态方程一般以隐式函数形式存在,不易进行非概率可靠性分析.笔者基于响应面方法对结构进行非概率可靠性分析,用二次多项式近似代替结构的极限状态函数,一方面避免了结构的隐式函数,另一方面可以提高工程结构计算效率.同时用RSM和FEM计算出的可靠性指标结果相差很小,验证了响应面方法的正确性和可行性.另外,笔者还比较了椭球模型和区间模型下的可靠性指标,算例表明两种模型都能较好地对结构进行可靠性分析,但区间模型相对于椭球模型更安全些.
参考文献:
[1]DOLTSINIS I, KANG Zhan. Robust design of structures using optimization methods[J]. Comput. Methods. Appl. Mech. Engrg, 2004(193): 2221-2237.
[2]ELISHAKOFF I. Essay on uncertainties in elastic and viscoelastic structures: from A.M Freuden-thal’s criticisms to modern convex modeling [J]. Computers & Structures, 1995,56(6): 875-895.
[3]BEN-H Y. A non-probabilistic concept of reliability [J]. Structural Safety,1994,14(4): 227-245.
[4]ELISHAKOFF I. Discussion on: A non-probabilistic concept of reliability[J]. Structural Safety, 1995, 17(3): 195-199.
[5]郭书祥,吕震宙. 结构的非概率可靠性方法和概率可靠性方法的比较[J].应用力学学报,2003,20(3):107-110.
[6]KANG Zhan, LUO Yang-jun, ALEX L. On non-probabilistic reliability-based design optimization of structures with uncertain-but-bounded parameters[J]. Structure Safety,2011(33): 196-205.
[7]郭书祥,张陵,李颖.结构非概率可靠性指标的求解方法[J].计算力学学报,2005, 22(2): 227-231.
[8]隋允康,宇慧萍.响应面方法的改进及其对工程优化的应用[M].北京:科学出版社,2010.
[9]JIANG Chao, BI Ren-gui, LU Guo-ying, et al. Structural reliability analysis using non-prob-abilistic convex model[J]. Comput. Methods Appl. Mech. Engrg, 2013(254): 83-98.
Analysis of Structural Non-probabilistic Reliability Based on Response Surface Method
CHEN Jiang-yi, WEN Wei-chao, WANG Ying-jia
(School of Mechanical Engineering,Zhengzhou University,Zhengzhou 450001,China)
Key words: non-probabilistic reliability;ellipsoid model;interval model;response surface method
