利用噪声能量和卡方分布约束的虚假锋电位筛除方法

利用噪声能量和卡方分布约束的虚假锋电位筛除方法

李志辉，刘新玉，尚志刚

(郑州大学 电气工程学院，河南 郑州 450001)

摘要：神经元锋电位可靠检测在神经科学研究与脑机接口应用中具有重要价值．针对低信噪比条件下锋电位检测的假阳性问题，提出了一种利用锋电位信号背景噪声能量和服从卡方分布约束的虚假锋电位去除方法.首先使用K-Means算法对过阈值检测的待判锋电位进行聚类，并用最小协方差算法估计各聚类总体噪声均值向量与协方差；进而计算各噪声样本与对应总体之间的马氏距离平方作为锋电位背景噪声能量和的度量指标；最后利用该指标卡方分布的置信区间对虚假锋电位进行筛除．不同信噪比条件下的仿真数据和动物实验数据应用结果表明:与传统的基于锋电位波形特征的阵列去噪算法相比，该方法可以有效识别出单电极记录神经信号中的虚假锋电位，正确率在95%以上，并且计算结果不依赖于聚类参数的选择．

关键词：锋电位检测；虚假锋电位；噪声能量和；马氏距离；卡方分布；K-Means聚类

收稿日期:2015-05-01；

修订日期：2015-06-29

基金项目:国家自然科学基金资助项目(U1304602,61473266,61305080)；河南省高等学校重点科研资助项目(15A120016)

作者简介:李志辉(1978—)，女，郑州大学讲师，博士生，研究方向为神经信号处理，E-mail：lizhrain@zzu.edu.cn.

通讯作者：尚志刚(1975—)，男，郑州大学副教授，博士，研究方向为数据挖掘与信号处理，E-mail:zhigang_shang@zzu.edu.cn.

文章编号:1671-6833(2015)05-0111-05

中图分类号：R318.04

文献标志码：A

doi:10.3969/j.issn.1671-6833.2015.05.024

Abstract:The reliable detection of neuronal spikes plays an important role from basic research in neuroscience to brain-machine interface applications. In order to solve the false positive problem in spike detection, a method was proposed to remove fake spikes, by using the chi-square distribution constraint of noise energy sum. First, the detected spikes over the threshold were separated by K-Means clustering, and the noise samples were acquired so that its means and covariance could be estimated by minimum covariance determinant (MCD) algorithm. Then, the Square of Mahalanobis Distribution (SMD) between each noise event and corresponding population was calculated to indicate the energy sum of noise. Finally, fake spikes were identified if their SMD value were not included in the confidence interval of corresponding chi-square distribution. The results from synthetic data and real neural data showed that the de-noising performance of this method is superior to the traditional methods. Its accuracy rate to identify the fake spikes is above 95%, and its performance is not dependent on the choice of clustering number.

0引言

神经元锋电位是利用微电极胞外记录方式检测到的神经元动作电位信息，对其可靠检测在神经信息编码机制、脑机接口研究中具有重要应用价值[1-2]．在神经电生理实验中，尤其是在信噪比较低的清醒动物神经信号采集中，微电极除了记录神经元放电活动之外，还会记录到大量的神经系统背景噪声、肌电干扰、电磁干扰、以及设备本底噪声等，尤其是背景噪声中的一些大幅值有色干扰，与锋电位具有相似的频域和时域特征，在以阈值为基础的检测方案中经常会被误检为锋电位，即产生假阳性问题，从而降低后续分析结果的准确性和可靠性[3-5]．

对于虚假锋电位的筛除，模板匹配是最简单最常用的方法，例如Quiroga等[6]通过对锋电位样本集聚类，将相似度低于给定阈值的样本作为虚假锋电位剔除．但该类算法去噪的性能很大程度上取决于聚类的结果，而虚假锋电位的存在同时又会对聚类效果造成干扰，去噪效果在低信噪比条件下不甚理想．Ludwig等[7]提出的共同平均参考去噪、Paralikar等[8]提出的虚拟参考去噪算法则是将不同通道的神经信号叠加平均作为参考信号，各通道信号与参考信号对消以去除大幅值干扰．此外，Paralikar等[4]还提出了电极间相关法(Inter-Electrode Correlation，IEC)用于去除虚假锋电位.这些利用多通道信号去噪算法的一个基本假设是认为噪声一旦发生就会被微电极阵列中多个电极同时记录到，而且波形相似．但是对于空间距离≥250 μm的两个电极而言，几乎不可能同时记录到来自于同一个神经元且波形相似的神经信号[6],而且各类有色噪声引起的大幅值干扰往往只会在单个通道中出现，无法利用上述阵列方法进行去除．万红等[8]采用多元小波阈值去噪算法用于去除锋电位检测中的大幅值干扰，吴丹等[9]采用主成分和小波阈值相结合的联合去噪方法用于去除锋电位检测信号中的有色噪声．但是这两种方法只有在不同通道锋电位信号之间相互独立并且包含相关噪声的情况下才能达到较好的效果，而且在去噪的同时也会对锋电位波形造成畸变，对后续锋电位分类造成影响．

鉴于上述方法存在的问题，笔者提出了一种利用噪声能量和卡方分布约束的虚假锋电位筛除方法，并利用仿真数据和动物实验数据对算法性能进行了对比评估．

1方法

1.1理论基础

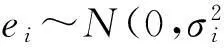
X～Np(μ,∑)．

(1)

式中：μ为总体均值向量;∑为协方差矩阵.

对于单个总体的多元空间异常值(或离群点)的检测，存在以下定理[11]：

对于n个p维空间中的样本X1,X2,…,Xn，如果Xi～Np(μ,∑)，i=1,2,…,n，∑>0，那么样本马氏距离(Mahalanobis Distance)的平方服从自由度为p的卡方分布，即

(2)

因此，总体中的异常样本可以通过设置卡方分布的1-α置信水平阈值来筛选，如果某个样本的平方马氏距离大于该阈值，则认为这个样本为异常值．

在实际应用中，检测到的多个锋电位通常来自多个总体，且总体的个数与均值都未知．无法直接应用上述单个总体异常值检测方法．笔者提出了一种间接思路，采用K-Means聚类，对于一个来自X～Np(μit,∑) 总体的锋电位，设其所属聚类的类别均值为μic，则有

ei=Xi-μic～Np(μit-μic,∑)．

(3)

对于属于一个聚类类别的样本，其类别均值都为μit，如果该类别样本确实来自同一总体，则该类样本与聚类均值的误差都服从相同的多元高斯分布，如公式(2)．根据前述单个总体异常值检验方法，该类噪声样本的马氏距离平方应服从卡方分布约束，表征了本底噪声的加权能量和．

为了保证聚类类别中的样本尽可能来自同一总体，在K-Means聚类中，给定的聚类个数应相对多些，这样一个真实的总体可能会分裂为多个子类，但聚类数过多会导致聚类后各类样本数过少，无法估计协方差．另外，考虑到单根电极同时能记录到的神经元活动一般为4个，最多不会超过8个[12]，因此在设置聚类数时，应保证其取值不小于真实的类别个数．

1.2虚假锋电位去除算法

在上述分析基础上，笔者提出一种利用聚类样本与类别均值误差的马氏距离作为锋电位辨别特征，根据卡方分布确定的阈值来筛除虚假锋电位.为便于描述，将这种算法命名为MDD(Mahalanobis Distance Denoising，MDD)算法．

在MDD算法中，最重要的步骤就是准确估计聚类后各类别中的噪声样本的均值与协方差．在采用K-Means算法获得各聚类样本与类别均值的噪声样本后，笔者采用最小协方差行列式(Minimum Covariance Determinant，MCD)算法对噪声的均值和协方差进行估计．MCD是一种常用的多元位置参数和尺度参数估计算法[13]，可以有效减小奇异样本对估计结果的影响，提高均值和协方差估计的鲁棒性．

综上所述，对于给定的多个锋电位事件样本，MDD算法的主要步骤如下.

① 对信号进行预处理，即将所有样本的负峰值点沿着同一竖线对齐．

② 利用K-Means算法对所有样本进行聚类，期望聚类数设为10～16个，计算聚类后各类样本个数．考虑到协方差估计的需要，因此在初步聚类后对于样本数较少的类别与其距离近的类别融合，保证各类中样本数大于特征维数p．

③ 利用MCD算法分别估计出每个聚类总体噪声样本的均值向量与协方差．

④ 利用式(2)计算噪声样本与对应聚类总体之间的马氏距离平方．

2算法应用结果

2.1仿真实验结果

参考文献为了测试MDD算法的性能，首先利用仿真数据对算法进行了验证．仿真数据来自[14]，由真实锋电位、背景噪声和虚假锋电位组成，真实锋电位分别来自于3个不同的神经元．虚假锋电位与真实锋电位具有相同的幅度水平和频带．仿真数据共由噪声水平分别为0.05、0.10、0.15、0.20、0.25、0.30、0.35和0.40的8段数据组成．噪声水平定义为背景噪声的标准差．图1为噪声水平为0.1时从仿真数据中检测出的信号波形及聚类结果，共包括521个锋电位及51个虚假锋电位．图1(a)为所有锋电位事件波形图(幅值经过方差归一化)；图1(b)为利用K-Means和MCD算法估计出的不同聚类的锋电位均值的波形图，此处设置K-Means的期望聚类数为16个；图1(c)为K-Means算法获得的不同类别的锋电位波形图．

图1　Spike仿真信号波形及其K-Means聚类

图2为从图1信号中获得的噪声及其马氏距离分布. 图2(a)中左图为从信号中提取的多个噪声波形，右图为其波形的幅值统计分布及高斯拟合曲线(拟合精度R-square=0.99)；图2(b)为噪声样本的马氏距离分布图，图中的直线是根据卡方分布设定的临界值，MDD算法共识别出了49个虚假锋电位，正确率96%.

表1为不同噪声水平下MDD算法的识别正确率.识别正确率定义为正确识别的锋电位个数(TP)与正确识别锋电位个数及漏检的锋电位个数(FN)和误判的锋电位个数(FP)之和的比(即TP/(TP+FN+FP)).由表1可知，在不同噪声水平下，MDD算法的识别正确率都在95%以上.

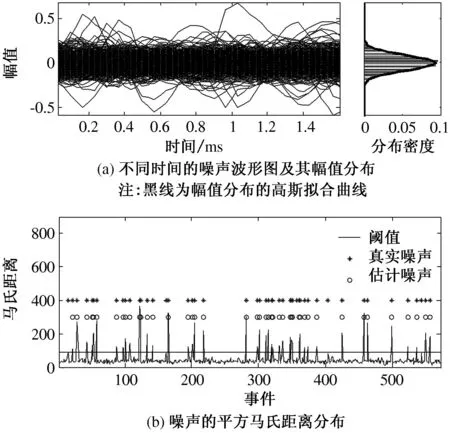
注：图中星号(*)标记的事件为真正的虚假锋电位；圆圈(∘)标记的事件为识别出的虚假锋电位.

图2　信号的噪声波形及其马氏距离分布

2.2实验结果

为了进一步测试算法的性能，笔者利用动物实验实测数据对MDD算法进行验证，并将其与多通道相关法IEC算法进行了对比.实测数据采用神经信号采集系统(CerebusTM，Blockrock Inc.)，在7只LE(Long Evans)大鼠V1区利用微电极阵列(Microprobe Inc.，2×8铂铱合金微电极阵列，电极阻抗在1 kHz下为0.5～1.0 MΩ)记录得到.视觉刺激和实验过程详见参考文献[15].采集后的信号使用通带为0.25～5 kHz的二阶带通Butterworth滤波器滤波，并采用内置的幅度阈值方法进行锋电位检测，各通道的锋电位检测阈值为4或5倍噪声标准差.将检测后的锋电位负峰值点沿同一竖线对齐.数据运算在MATLAB 7.6.0(R2008a)环境下进行．从7只大鼠共112个通道中去除无效通道后(信噪比较差或检测到的事件个数小于500的通道被视为无效通道)，共提取了46个有效通道．

MDD算法与IEC算法的对比结果如图3所示.图3(a)为信号最大的两个主成分散点图，由图可见，IEC算法识别出的虚假锋电位大多离聚类中心较近，而MDD算法识别出的大都远离聚类中心. 图(b)和(c)分别为IEC算法和MDD算法识别出的有效锋电位波形图，对比二者可以看到，采用MDD算法筛除虚假锋电位后的锋电位波形变异要明显小于IEC算法．

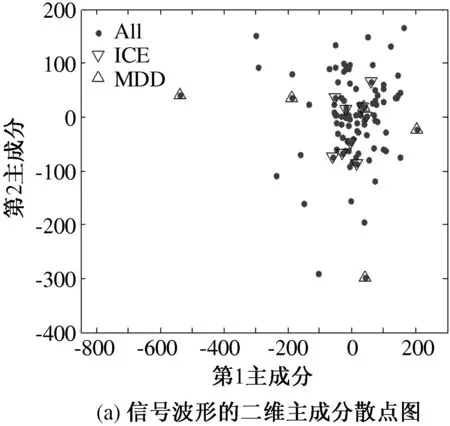
注：图中灰色圆点(•)代表记录到的事件;黑色下三角形(▽)为IEC算法识别出的虚假锋电位;黑色上三角形(△)为MDD算法识别出的虚假锋电位．

图3　IEC算法和MDD算法识别结果对比图

(4)

其中单个锋电位的信噪比计算公式为

(5)

式中：std(·)为标准差；max(·)为最大值；min(·)为最小值．

噪声标准差为各锋电位信号噪声成分的平均标准差，计算公式为

(6)

获得的46组神经信号在去噪前、IEC算法去噪后、MDD算法去噪后的信噪比、噪声标准差对比结果如表2所示．经过去噪之后，MDD算法去噪后信号的信噪比高于IEC算法(p<0.05)，而噪声能量低于IEC算法(p<0.05)，展现出良好的去噪性能．

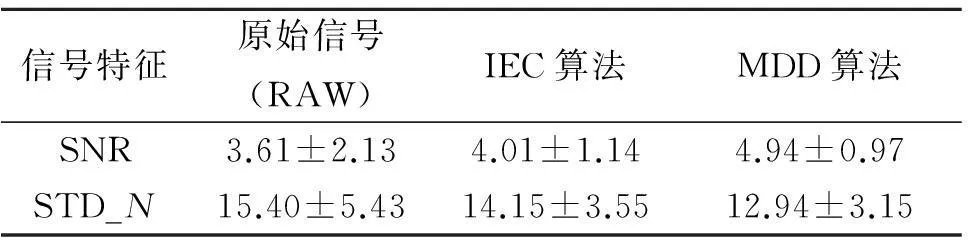
表2　IEC算法和MDD算法去噪性能对比

3结论

通过对实验结果的分析可以看到，笔者提出的MDD算法可以有效识别出锋电位中混杂的虚假锋电位事件，识别正确率在95%以上；与基于多通道信息的IEC算法相比，MDD算法表现出了更好的去噪效果．仿真数据和实测数据的应用结果表明，笔者提出的MDD算法可以有效筛除神经信号中的虚假锋电位．

虚假锋电位的筛除目前并没有通用有效的方法．笔者提出的MDD算法是一种单通道去噪算法，利用真实锋电位背景噪声能量和应服从卡方分布这一约束来实现对虚假锋电位的辨别，可以避免如平均参考去除、小波分解等算法在锋电位检测前进行去噪而造成信号畸变、识别准确率下降的问题．此外，MDD算法中虽然采用了K-Means聚类，但并不需要精确对锋电位进行聚类，聚类数目的选择并不影响虚假锋电位的筛除效果．不过，MDD算法会把叠加的锋电位信号识别为虚假锋电位，因此对于识别出的虚假锋电位事件还需要进一步筛选出叠加锋电位信号，并利用相应的方法进行解耦合处理．

[1]HOHL S S, CHAISANGUTHUM K S, LISBERGER S G. Sensory population decoding for visually guided movements[J]. Neuron, 2014, 79(1): 169-179.

[2]BECEDAS J and QUIROGA R Q Real time decoding for brain-machine interface applications[J]. Journal of Bioinformatics and Biological Engineering, 2014, 2(1): 20-32.

[3]WAN Hong, LIU Xin-yu, NIU Xiao-ke, et al. The design and implementation of anti-interference system in neural electrophysiological experiments[J]. Electrical Engineering and Control, Lecture Notes in Electrical Engneering, 2011(98): 605-611.

[4]PARALIKAR J K, RAO C R, CLEMENT R S. New approaches to eliminating common-noise artifacts in recordings from intracortical microelectrode arrays: inter-electrode correlation and virtual referencing[J]. Journal of Neuroscience Methods, 2009, 181(1): 27-35.

[5]HILL D N, MEHTA S B, KLEINFELD D. Quality metrics to accompany spike sorting of extracellular signals[J]. Journal of Neuroscience, 2011, 31(24): 8699-8705.

[6]QUIROGA R Q, NADASDY Z, BEN S Y. Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering[J]. Neural Computation, 2004, 16(8): 1661-87.

[7]LUDWIG K A, MIRIANI R M, LANGHALS N B, et al. Using a common average reference to improve cortical neuron recordings from microelectrode arrays[J]. Journal of Neurophysiology, 2009, 101(3): 1679-1689.

[8]万红, 李晓燕, 刘新玉, 等. 锋电位检测信号的多元小波去噪方法研究[J]. 系统仿真学报, 2013, 25(10): 2487-2498.

[9]吴丹, 封洲燕, 王静. 微电极阵列神经元锋电位信号的去噪方法[J]. 浙江大学学报:工学版, 2010, 44(1): 105-110.

[10]FAISAL A A, SELEN L P, WOLPERT D M, Noise in the nervous system[J], Nat Rev Neurosci, 2008, 9(4): 292-303.

[11]高惠璇. 应用多元统计分析[M].北京：北京大学出版社, 2005.

[12]PEDREIRA C, MARTINEZ J, ISON M J, et al. How many neurons can we see with current spike sorting algorithms[J]. Journal of Neuroscience Methods. 2012, 211(1): 58-65.

[13]HUBERT M, DEBRUYNE M, Minimum covariance determinant[J],Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(1):36-43.

[14]MARTINZE J, PEDREIRA C, ISON M J, et al. Realistic simulation of extracellular recordings[J]. Journal of Neuroscience Methods. 2009, 184(2): 285-293.

[15]刘新玉. 神经元锋电位干扰抑制算法研究及实现[D]. 郑州：郑州大学电气工程学院, 2012.

A Method to Remove Fake Spikes by Means of Chi-Square Distribution

Constraint of Noise Energy Sum

LI Zhi-hui, LIU Xin-yu, SHANG Zhi-gang

(School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China)

Key words: Spike detection; fake spike; noise energy sum; mahalanobis distance; chi-square distribution; K-Means clustering