压缩感知的人脸图像去噪

林克正++魏颖+程卫月

摘要：为解决人脸识别领域的噪声图像恢复问题，提出一种压缩感知的人脸图像去噪算法，协同稀疏性度量（collaborative sparse measure，CSM）. CSM算法利用图像的先验知识，用一个域将图像稀疏表示，将图像的二维稀疏表示和三维稀疏表示同时进行自适应混合空间域转换，利用增广拉格朗日技术求解.实验结果表明，CSM算法的信噪比明显高于传统算法的信噪比，具有高效性.

关键词：压缩感知；协同稀疏性度量；图像去噪；空间域

DOI：10.15938/j.jhust，2015.05.018

中图分类号：TP391.4

文献标志码：A

文章编号：1007-2683（2015）05-0091-06

0 引言

压缩感知的基本思路是对数据进行变换后，完成从较少的数据中提取较多的信息，压缩感知理论为传统的信息处理打开了新的篇章.目前，在对图像噪声滤除方面，常用的算法有树结构小波（tree-structured wavelet，TSW），树形结构的离散余弦变换（tree-structured wavelet discrete cosine transform，TSWDCT），总度差（total variation，TV）等，它们能不同程度地滤除图像噪声，恢复图像本身.针对高斯噪声干扰人脸图像这一问题，本文提出协同稀疏性度量（CSM）来对噪声图像进行恢复，该算法利用图像的先验知识，寻求一个基，并利用图像的局部平滑特性和非局部自相似性质，其中二维稀疏表示利用到图像的垂直梯度和水平梯度对图像滤波，三维稀疏表示首先将赝本划分成n个大小相等的块，寻找最佳匹配块进行三维转换，最后用增广拉格朗日技术求解，提高滤除图像噪声的能力，恢复图像本身.

1 压缩感知理论和增广拉格朗日方法

1.1 压缩感知理论

一个长度为Ⅳ的信号U在基ψ下是稀疏的，如果它的变换系数是零或接近于零，则稀疏的量化是通过系数向量里重要元素的个数来决定，具体地，给定M个线性测量，b个信号U的压缩感知恢复问题是如式（1）约束的优化问题.

A表示随机投影.P通常被设置成1或0，特征向量的稀疏性为 是l₁范数，当 是l₀范数时给向量加上绝对值，并且计算向量的非零元素.压缩感知理论是能够从b个样本M中恢复出稀疏信号U，前提是随机样本的数量M≥aK.所需要的样本采样率为M/K，为了完全恢复样本，比例应该为K/N.

1.2 增广拉格朗日方法

式（2）为线性约束问题.增广拉格朗日函数的定义为式（3）.

2 基于压缩感知的噪声图像恢复算法

2.1 算法的提出

该方法采用人脸图像的两种先验知识，即自然图像的局部平滑和非局部自相似性，而图像的稀疏性能和自然图像的两个性能一致.

一个通用的稀疏性度量类型可被描述成通过压缩感知恢复的高保真图像，称作协同稀疏性度量.建立一个自适应数据混合空间变换域，这个域合并另外两个互补的稀疏的局部二维域 和非局部三维稀疏域 .

P和Q通常被设置在[0，1]之间，a是一个正规化参数，ψ_L2D对应于上述的先验知识局部平滑，保持图像的局部一致性，有效地抑制噪声，ψ_N3D对应于上述的先验知识局部自相似性，保持图像非局部一致性，同时保持锐利且边缘有效.

2.2 特征设计

2.2.1 空间域的局部二维特征

对于自然图像，首选响应尽可能小的一组滤波器，因为滤波后的图像和高通滤波器的一些卷积是稀疏的，大多数像素强度接近零，这种类型的稀疏性为空间域的局部二维稀疏.

实践中广泛使用的滤波器是水平和垂直的差分算子，用D_v和D_h表示，这分别对应于垂直梯度和水平梯度的图片，不失一般性，梯度图像是由广义高斯分布模拟.令 ，另p在式（4）中实现空间域ψ_L2D的局部二维稀疏，如式（5）.

对于各项异性的总变化，ψ_L2D。具有相同的表达式.在本文中，ψ_L2D经常被用来描述自然图像的局部平滑，ψ_L2D也可以取代二阶导数或更复杂的学习过滤器，p被设置成1/2或1/3的超拉普拉斯先验知识.

2.2.2 非局部的三维稀疏变换域

非局部的自相似性体现一些稀疏度量的属性，借助于系数的稀疏性和整合来重塑自相似性，取得通过堆叠相似图像的斑点转化产生的3D组，这种稀疏性为非局部的三维稀疏变换域，

如图1所示，对于每个块，找到在一个搜索窗口相抵的块，那些块被堆积在一个3D的数组内.为获得系数，在一个3D数组内进行3D转换，用非零系数的数目来衡量这个斑点的非局部3D稀疏性，通过整合所有块来取得整幅图像的非局部3D稀疏性，

逆算子A_N3D的定义为：在获取Φ_X以后，将它分割为n组3D变换系数，然后再逆序产生每一块的估计值，用每一块的估计值返回到它们的原始的位置，最终的图像估计值为所有块的平均值估计，其中，X的估计值为 .

2.3 协同的稀疏测量

非局部的三维稀疏利用自然图像的自相似性，借助于稀疏系数来表示自然图像的自相似性特征，并由转化3D组产生的堆叠相似图像块获得.稀疏性不仅能够保留自相似块中的纹理特征，也能在一定程度上保持不同块中的不同特征.因此，提出用协同稀疏性度量来解决噪声图像的恢复问题.

考虑到整体的局部平滑性和非局部自相似性，CSM在空间域局部2D稀疏性和变换域非局部3D稀疏性的表示如式（7）.利用稀疏的高度性，将自然图像映射到高维自适应混合空间变换域，限制了CSM的解空间.

3 实验结果与分析

实验采用的人脸图像为两张灰度图像和一幅自然图像，用matlab2010进行测试.每个块的大小B_S设置为8x8，待测窗口搜索块的大小设置为41×41，经验值为1，μ=28，0=2，，本文中β=32或卢= 64，τ=8或τ=12.

3.1 滤除图像噪声实验

用树结构小波算法，树形结构的离散余弦变换算法和总度差与本文方法作比较，用图像的信噪比（signal-to-noise ratio，SNR）表现结果，信噪比的单位用dB表示.

将图3中受高斯噪声干扰的人脸图像用4种方法进行恢复，其中，图3中的3幅人脸图像受到了同样的高斯噪声干扰.图4、图5、图6分别为TSW算法、TSWDCT算法、TV算法和本文算法对图像去噪后的效果，从左到右显示序号分别为算法1、2、3和4，可看到本文算法的恢复效果最好.

表1展示了4种方法在不同情况下的信噪比，由表1可以看出，本文方法的平均信噪比比TSW算法平均高8.49dB，比TSWDCT算法平均高5.23dB，比TV算法平均高的3.49dB，所以本文方法有很好的滤除图像噪声来恢复图像的能力，

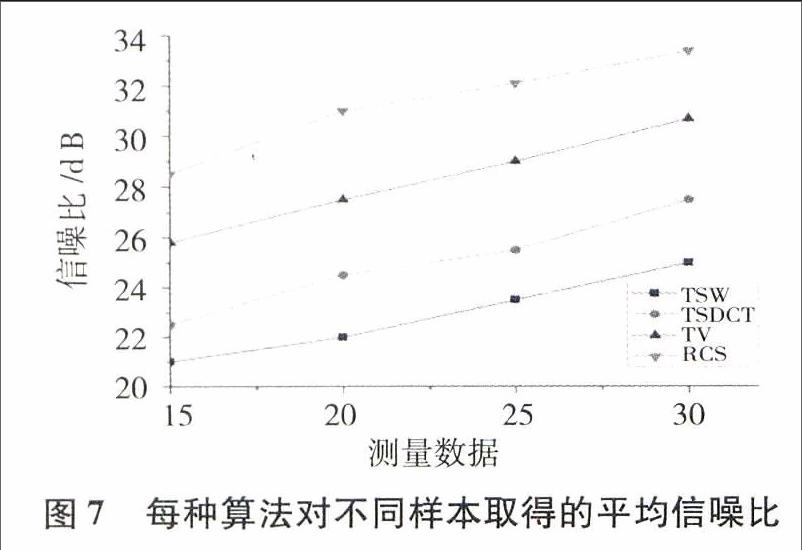
每种算法对不同样本取得的平均信噪比结果如图7所示，看到本文算法的最高信噪比可达到接近34dB，比TV算法的接近31dB高出3dB，跟TSW和TSDCT两种算法比较高出的更多，足以说明本文方法的高效性.

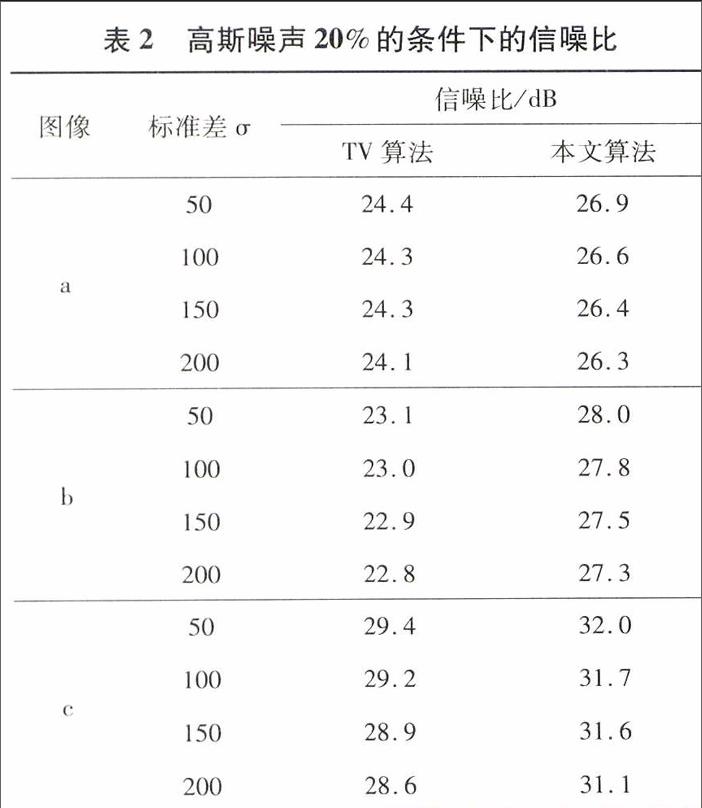
表2和3显示了3幅图片的高斯噪声在20%和30%的情况下，并且标准差σ从50到200不等的情况下的信噪比结果，由于TV算法和本文算法对高斯噪声都是稳定的，所以对这两种算法做比较，从表2和表3可看出，本文算法对图像噪声的滤除能力明显高于TV算法，

表4显示了两种算法在上述情况下的执行时间，本文算法的执行时间是TV算法的执行时间的两倍左右，这是因为本文算法的复杂度高造成的.

图8描绘了不同比率下测量图像的信噪比与迭代次数的关系.迭代次数增加，图像重建的信噪比快速增加并趋于稳定.从图8曲线看出图像不光滑，迭代过程中有尖点，导致这种情况原因有二，一是原函数具有凸性，另一原因是本文算法避免收敛于局部最优解而试图实现全局最优解

4 结语

本文提出了一种压缩感知的人脸图像去噪算法，该算法以压缩感知理论为基础，引入协同稀疏性度量，一方面，有效地刻画自然图像中固有的稀疏自适应空间变换域；另一方面，该算法对高斯噪声稳定，更有利于滤除图像噪声，恢复图像本身.该算法与其他算法相比，滤除图像噪声能力强，且压缩感知理论在滤除图像噪声中颇具潜力.