面齿轮传动系统非线性动力学键合图模型及方程
2016-01-19宋野于广滨戴冰高德军葛江
宋野++于广滨++戴冰++高德军++葛江华


摘要:为了较好研究面齿轮的传动系统,本文以正交面齿轮传动系统为研究对象,基于Bondgragh理论建立了综合时变啮合刚度、传动误差、齿面摩擦力、啮合阻尼等因素的耦合非线性动力学模型.运用Bond gragh理论将面齿轮传动系统中的激励和响应转化为键合图元,分析系统运动的特性分别建立了面齿轮弹性变形键合图模型、传动误差键合图模型和齿面摩擦键合图模型,并分析因果关系和键合图中的功率流得到面齿轮传动系统非线性动力学耦合方程.
关键词:面齿轮;动力学;键合图;非线性
DOI: 10.15938/j.jhust.2015.05.010
中图分类号:TH113
文献标志码:A
文章编号:1007-2683(2015)05-0051-05
0 引言面齿轮除了具有大重合度、强轴间位置适应性、大变速比外,面齿轮传动还具有大传递功率、良好的分流效果、优良的工作平稳性、简单结构、低噪声、轻单位质量、小空间占用等优点,其应用领域广泛覆盖.经过长期的理论研究和技术实践,在国内外的众多研究机构和学者的努力下,对面齿轮传动系统结构的研究也更加深入和细化,重点研究领域主要有:面齿轮的齿面成形原理及啮合动态特性,基于有限元法的面齿轮结构强度、温度场分布,面齿轮的实际生产加工及制造装备,动力学分析与实验测量方法的研究.
Bond graph理论是由美国麻省理工学院的H.M.Paynter教授在1959年提出的,其理论基础是热力学第一定律,即热量可以从一个物体传递到另一个物体,也可以与机械能或其他能量互相转换.具体形式是分析机械系统中的多种能量范畴耦合合成的基本物理过程,用四中形式的广义变量:势、流、广义动量和广义位移描述系统功率的传输、转化、贮存、耗散,并按照相互链接关系、能量传输情况、变量间因果关系、系统阶次等系统信息将与能量单元相关的理想元件用键连接,因此键合图可以更加形象具体的表现机械系统尤其是面齿轮系统的非线性传动特性,所用的状态变量即为系统的物理变量,在机械系统中各机械元件相互作用综合,是系统的输入与输出保持某种因果关系,其因果关系具体表现为各元件之间的功率传递,这也是Bond graph理论的根本依据.根据机械系统的工作原理,按照各元件的因果关系,即可建立起系统的键和图模型,分析其隐含着的系统动态性能状态方程,增广后可列写出相应的动力学方程.
1 面齿轮传动系统的键合图建模
1.1 弹性变形模型
面齿轮轮齿在啮合过程中,在齿面载荷的作用下会发生形变.在轮齿任意位置的弹性变形δ与相应受到的载荷W具有如下关系
W=khf(δ).
(1)式中:kh即轮齿的综合啮合刚度.根据Bond graph理论,载荷W定义为势变量e(t),弹性变形δ定义为广义位移F(t),那么面齿轮轮齿的弹性变形可用基本的一端口元件容性元C来表示,参数为kh.
由于齿轮在加工、制造与安装、运转过程中会产生误差,从而导致啮合齿廓偏离其理论位置,进而在轮齿啮合过程中产生位移型激励,即为误差激励.因此可用流源Sf表示面齿轮传动系统中误差激励en(t)的导数,面齿轮传动误差激励的键合图模型如图1所示,容性元件C表示弹性变形,阻性元件R表示啮合阻尼,并且流源S,可以定义为
1.2 齿面摩擦模型
图2所示为一对相互啮合传动的面齿轮传动副,根据牛顿第三定律可知圆柱齿轮和面齿轮所受的摩擦力大小相等、方向相反.滑动摩擦力产生于主动轮和被动轮的齿面在轮齿啮合的过程中发生相对滑动的过程中,因此与啮合线相垂直的方向是摩擦力的方向,
基于库伦摩擦定律(Coulomb定律),摩擦力Ff可以定义为式中:μ为摩擦系数;sign表示符号函数,FN为正压力,
根据Bond graph理论,齿面摩擦力为耗能元件,且不断变化,因此可以应用一端口元件阻性元MR表示.根据公式可知由于摩擦力臂Z的变化导致齿廓接触点间的相对速度Vh发生变化,进而影响摩擦力Ff改变,因此可以应用二端口元件变换器MTF来表示圆柱齿轮和面齿轮的摩擦力臂l变化,可得出面齿轮齿面摩擦的键合图模型如图3所示.
1.3 包含齿侧间隙的时变刚度模型
齿轮啮合传动时,为了在啮合齿廓之间形成润滑油膜,避免因轮齿摩檫发热膨胀而卡死,齿廓之间必须留有间隙,此间隙称为齿侧间隙.一般情况下齿侧间隙很小,但由于其误差的存在,会使得齿轮在啮合时产生啮合冲击,对于齿轮的平稳性和啮合的动态特性造成很大的影响,甚至降低齿轮系统寿命,影响整个机械系统的正常运转.上文公式提到面齿轮系统刚度kh的定义,其中f(*)即为齿轮啮合时考虑齿侧间隙的函数,考虑该函数对面齿轮传动系统动力学模型具有非线性的影响,传统的基本键合图元件无法详细表述,可采用一种非线性元件功率结型结构来形容.
如图4所示,齿侧间隙模型可由两个质量元件m1和m2、一个间隙非线性弹性元件kf(*)和一个能量耗散元件C所组成.当齿轮系统中间隙大小为2b时,可以定义f(*)为非线性分段函数,表示为
根据Bond graph理论,由于间隙函数f(*)是联系势变量e(t)(即载荷W)和广义位移q(t)(即弹性变形δ的函数,可以用一端口容性元件C定义,容度参数即为l/kh.由于间隙函数f(*)具有分段性特征,在建立键合图模型时需要引入布尔变量u来表述函数的时变性.相对于齿侧间隙的3个状态,分别用ui(i=1,2,3).定义:u1:w=kh(δ-b),δ>b;u2:w=0,-b≤δ≤b;u3:w=kh(δ+b),δ<-b.并且当3个布尔变量中一个为1,其他两个即为0,这样可以用布尔变量u来控制功率结中的功率通口.
图5考虑齿侧间隙的时变刚度键合图模型
图5所示即为根据齿轮冲击副模型建立的考虑齿侧间隙的时变刚度键合图模型,定义状态变量δi(i=1,2,3),可得到该键合图模型的状态方程
1.4 齿轮弹性支撑的键合图模型
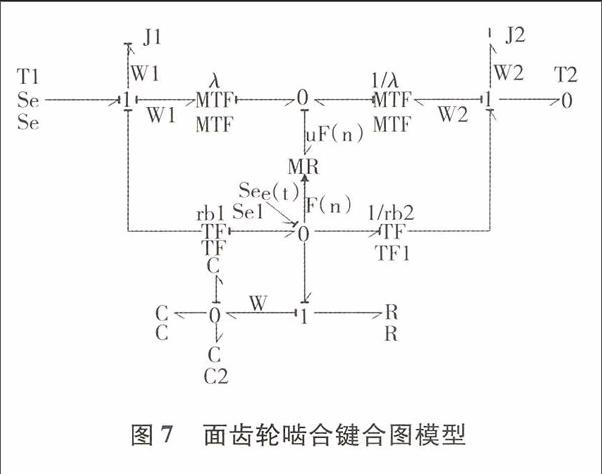
基于啮合原理和面齿轮传动的实际特点可知,主动轮为圆柱齿轮,在其轴向没有力的作用存在,从动轮为面齿轮,在其径向没有力的作用存在,因此面齿轮传动系统中圆柱齿轮和面齿轮轴承弹性支撑的动力学模型可分别用两个弹簧和阻尼器模拟,模型如图7所示.
模型中m1,m1分别为圆柱齿轮和断齿轮的集中质量;根据Bond graph理论,齿问的载荷力的分量和齿间摩擦力的分量可用一端口势源元件Se表示,支撑刚度kx1,kz1,kx2,kkz2,可用一端口容性元件C表示,阻尼Cx1,Cz1,Cx2,Cz2由于造成功率损耗可用一端口阻性元C表示,齿轮集中质量m1,m2可用一端口惯性件,表示.
齿轮瞬时传动比会因为齿轮加工误差和安装误差等误差因素的存在发生变化,产生轮齿间碰撞冲击现象,误差在键合图中可以用一端口势源Se表述.根据Bond graph理论,结合如图6所示的面齿轮非线性动力学模型,可以得到面齿轮非线性啮合的键合图模型如图7所示.
2 键合图模型方程推导
上文分析面齿轮传动系统中圆柱齿轮和面齿轮只在x轴和z轴存在弹性支撑,因此存在四个弹性支撑的键合图模型,根据啮合理论弹性支撑的存在是由于轮齿啮合时齿轮副间碰撞冲击,产生动载荷和摩擦.齿轮弹性支撑键合图模型中的容性元C、惯性元,和阻性元R的线性形式因果关系分别是
其中k为齿轮的支撑刚度;m为齿轮的质量;c为阻尼,利用1结约束条件和按照已指定的因果关系,就可得到该系统的状态方程为
由于弹性支撑方向与动载荷方向相关,分析可知圆柱齿轮和面齿轮受到的弹性支撑沿各自轴向且方向不同,当通过弹性支撑键合图模型推导动力学方程时,应该考虑输入变量势源Se的不同,即Fk+Fn不同.齿啮合时齿轮副受到的法向动载荷Fn及其沿x,z坐标轴上的分量为
圆柱齿轮在沿x轴的横向振动是受到啮合齿面的法向载荷Fn沿x轴正方向的分力和摩擦力fx的共同作用即变量势源Se分别表示为
面齿轮同理,因此根据图6所建立的面齿轮传动系统中弹性支撑的非线性动力学方程为式中λ为摩擦力方向函数;lp为时变摩擦力臂.已知齿轮副重合度ε,小齿轮基圆半径rb1,小齿轮齿顶圆半径ra1,小齿轮基圆齿距Pb1,小齿轮转速n1,则摩擦力臂lp及摩擦力方向函数 可表示为:
根据Bond graph理论,面齿轮啮合键合图列写动力学方程需确定系统的输入变量和状态变量,分别选定,元的广义动量P2,p9和C元的广义位移δ为状态变量,势源SeT1,T2为输入变量,键合图模型中的容性元C、惯性元I和阻性元R的线性形式因果关系分别是
其中:kh为两齿轮的啮合刚度;I1,I2为两齿轮的转动惯量;ch为两齿轮的啮合阻尼.利用1结约束条件和按照已指定的因果关系,就可得到该系统的状态方程为
对键合图中功率传输方向进行分析,可得出系统中势变量和流变量如下
3 结论
本文应用Bond graph理论建立了正交面齿轮传动系统动力学模型,并推导了面齿轮传动系统动力学方程,与传统动力学研究方法相比具有以下优点:
1)基于Bond graph理论建立的面齿轮传动系统动力学方程,综合考虑了系统的时变啮合刚度、啮合误差、啮合阻尼、齿间摩擦等非线性因素,对于齿轮系统变化状态的描述具有较好的准确性.
2)基于Bond graph理论建立的面齿轮传动系统动力学模型,由于只用四种形式的广义变量皆可以把面齿轮传动系统中物理过程表述出来,对于系统中各个物理量的关系和能量变化情况比较直观,并且灵活性和拓展性较高,可根据实际情况在模型中添加或是减少影响系统的激励因素.
3)根据已建立的键合图模型推导面齿轮动力学方程,不但符合齿轮啮合的实际情况,而且由于其清晰的因果关系,对于方程的推导效率和准确程度也较满意.
