基于精细积分法的结构碰撞反应谱研究

第一作者 尹俊红 女，博士生，1986年生

通信作者 李青宁 男，教授，博导，1952年生

邮箱：lqn952@163.com

基于精细积分法的结构碰撞反应谱研究

尹俊红，李青宁，张瑞杰，程麦理，闫磊，孙建鹏，韩春

(西安建筑科技大学 土木工程学院，西安710055)

摘要：碰撞是导致结构地震破坏的重要原因之一，其与两碰撞结构的动力性能和地震作用密切相关，应给出与两个结构动力参数相关的反应谱，以指导结构考虑碰撞的抗震设计。本文给出相邻结构碰撞加速度反应谱定义，推导了精细积分法碰撞计算公式，进行了该反应谱曲面的分析和探讨。结果表明，精细积分法适用于结构碰撞问题的计算，可得到高精度的解，无条件稳定且可提高计算效率。碰撞会加大结构的加速度响应；动力特性相同的两相邻结构产生的响应有差异；增大阻尼比和相邻结构阻尼比差别、以及设置足够大的初始间隙，可有效降低结构的碰撞响应。

关键词：结构碰撞；精细积分法；加速度反应谱；阻尼比；间隙

基金项目：国家自然科学基金资助项目(51078306)；国家自然科学基金资助项目(51408453)；高等学校博士学科点专项科研基金资助项目(20106120110004)；高等学校博士学科点专项科研基金资助项目(20136120120022)

收稿日期：2014-07-24修改稿收到日期：2014-09-30

中图分类号:U442.55文献标志码： A

Structural impact response spectra based on precise time-integration method

YINJun-hong,LIQing-ning,ZHANGRui-jie,CHENGMai-li,YANLei,SUNJian-peng,HANChun(College of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Abstract:Collision is one of the main reasons leading to damage of structures under earthquake excitation,it is closely related to structures’ dynamic characteristics and earthquake action. Response spectra for two adjacent impacting structures related to their dynamic parameters should be deduced to guide their aseismic design considering impact. Here, acceleration response spectra for impact between two adjacent structures were defined, the calculation formulas of pounding based on precise time-integration method were derived,and the response spectra were analyzed and discussed. The study results indicated that the precise time-integration method with high accuracy, unconditionally stable and improved efficiency is suitable for the computation of structural impact problems; acceleration responses of structures increase due to pounding, the responses of two adjacent structures with the same dynamic characteristics are different; to increase damping ratios of the two structures and the difference between the two ratios, and to set up enough large initial gap between the two structures can effectively reduce their impact responses.

Key words: structural pounding; precise time-integration method; acceleration response spectrum; damping ratio; gap

碰撞会对结构造成极大损害[1-2]，碰撞问题被认为是影响结构地震反应和抗震性能的一个重要因素。

利用精细时程积分法无条件稳定、精度高和受时间步长限制小的特点，将其引入求解结构的碰撞问题，验证精细积分法的计算精度和适用性。并基于精细积分法进行了结构的碰撞加速度反应谱研究，反应谱表明具有指定阻尼比和频率的单自由度结构对地面输入的反应程度[8]，是根据地震对单自由度结构的最大影响来表征地面运动特性。对于碰撞问题的反应谱研究，Kawashima等[9]给出了相邻结构最大位移反应谱，Ruangrassamee等[10]给出了碰撞影响下的相对位移反应谱，王君杰等[11]给出桥梁结构受撞击的位移冲击谱及统计规律，Jankowski R[12]给出结构碰撞力反应谱。相对位移谱可用于指导结构防撞设计中初始间隙的设置；碰撞力反应谱用于评估结构因碰撞造成的潜在损害，并为防撞墙和缓冲装置的设计直接提供碰撞力最大值。以上内容对结构的碰撞问题研究提供了有益的指导，但目前还鲜见针对相邻结构碰撞加速度反应谱的研究与探讨，加速度谱可反映碰撞引起的结构加速度响应相对于地面输入地震波的放大效果，并直接得到考虑碰撞的最大地震作用，而后即可根据反应谱理论将其看做静力作用对结构进行强度和刚度等验算，以指导结构进行考虑碰撞的抗震设计。基于精细积分法，考虑了结构的阻尼比和初始间隙等参数，进行了结构的碰撞加速度谱分析，为相邻结构的碰撞研究和抗震设计提供参考。

1精细积分法在碰撞中的应用

1.1碰撞理论

结构碰撞理论分析模型见图1，碰撞结构体系的动力平衡方程为：

(1)

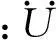
图1　理论模型 Fig.1 Theoretical model

在碰撞的理论以及模拟分析中，通常采用接触单元模拟结构的碰撞力。Jan-Hertz-damp模型(非线性-阻尼模型)[13]假定在相互接触的阶段，有可能发生塑性变形和局部损伤现象，且能量耗散仅在此过程发生；在分离阶段，积累的弹性应变能开始释放，此阶段没有能量耗散。采用Jan-Hertz-damp模型模拟结构的碰撞力，接触过程中的碰撞力表示为：

(2)

(3)

1.2精细积分法求解

对式(1)采用精细积分法求解：

令

(4)

有

(5)

(6)

式(5)和式(6)代入式(1)，有

(7)

整理为：

(8)

令

x=[U1(t)U2(t)p1p2]T

(9)

(10)

(11)

式(8)可化为：

(12)

式(12)即为结构碰撞问题的状态传递方程。一般解为[14]：

(13)

将荷载作用离散成步长Δt时间间隔，任意时刻表示为kΔt(k=0，1,2…)，tk+1=tk+Δt，则

(14)

(15)

(16)

令T(Δt)=eHΔt

(17)

指数矩阵T(Δt)求解如下：

(18)

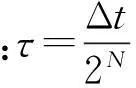
将指数矩阵展开为泰勒级数：

T(τ)=eHτ=I+Ta

(19)

(20)

式中:l为截断阶数。

由于Ta的元素值非常小,若它与直接矩阵I相加后进行式(18)的运算，会由于计算机的舍入操作而丧失精度。为避免这一问题，式(18)计算过程如下：

(Ta)t+1=2(Ta)i+(Ta)i·(Ta)i

(i=1,2,…,N)

(21)

计算得到(Ta)N，则

T(Δt)=l+(Ta)N

(22)

精细积分法的计算过程通过编程语言实现，求解过程为：

(2) 根据式(17)得离散时刻tk的状态向量，其前两项即为位移U1(tk)、U2(tk)。

(4) 若相对位移不超过初始间隙，Fc(tk)=0；若相对位移超过初始间隙，采用式(2)计算Fc(tk)，并进行下一步迭代。

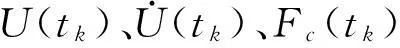
(6) 重复以上“(2)”～“(5)”步骤，直至地震动输入完成。输出计算结果。

2精细积分法验证

为验证精细积分法的精度和适用性，通过对两小球自由弹性碰撞进行模拟，图1中间隙d=0，两小球质量均为 2 kg，自振圆频率为10.25 rad/s，左侧小球从初始位置向右侧自由运动与右侧小球发生弹性碰撞，初始时刻位U1(0)=0.1 m,U2(0)=0。假定碰撞过程中无能量损失。

满足动量守恒的结构位移响应理论解见图2(a)；采用Newmark-β法和Willson-θ法传统时程分析方法，以及所提出的精细积分法求解的位移响应见图2(b)图2(d)，求解积分时间步长取0.000 1 s和0.000 2 s。由图2可知，Newmark-β法和Willson-θ法采用0.000 1 s积分步长的计算结果与理论解有较大误差，只有取更小的积分步长才可使其精度增加；且传统时程积分方法受时间步长影响较大，随着时间的推移，误差在积分步长采用0.000 2 s时较0.000 1 s明显增加，此时计算稳定性较差。而精细积分法采用0.000 1 s积分步长的计算结果与理论解非常接近，表明与传统积分法采用相同积分步长时，其计算精度较高；积分步长取0.000 2 s的计算结果仍然与理论解吻合，说明该方法在碰撞问题计算中也很稳定，且总体计算误差较其它两种方法小很多，这也意味着选择相对较大的积分步长不但保证精度和稳定性，还可以使计算效率提高。

采用精细积分法计算的碰撞力时程见图3，可以看出，基于精细积分法求解的结构位移时程与理论位移时程的峰值和相位一致，精细积分法求解的碰撞次数为6次，总体与理论相符，但碰撞位置有细微变化，并且随着时间推移差异有些许的增加趋势，这是因为理论解满足动量守恒定律，碰撞是在瞬间完成的，而采用接触模型的碰撞力总是有作用过程，这一过程随着接触碰撞刚度的增大而减小，其位移解也更接近理论解。

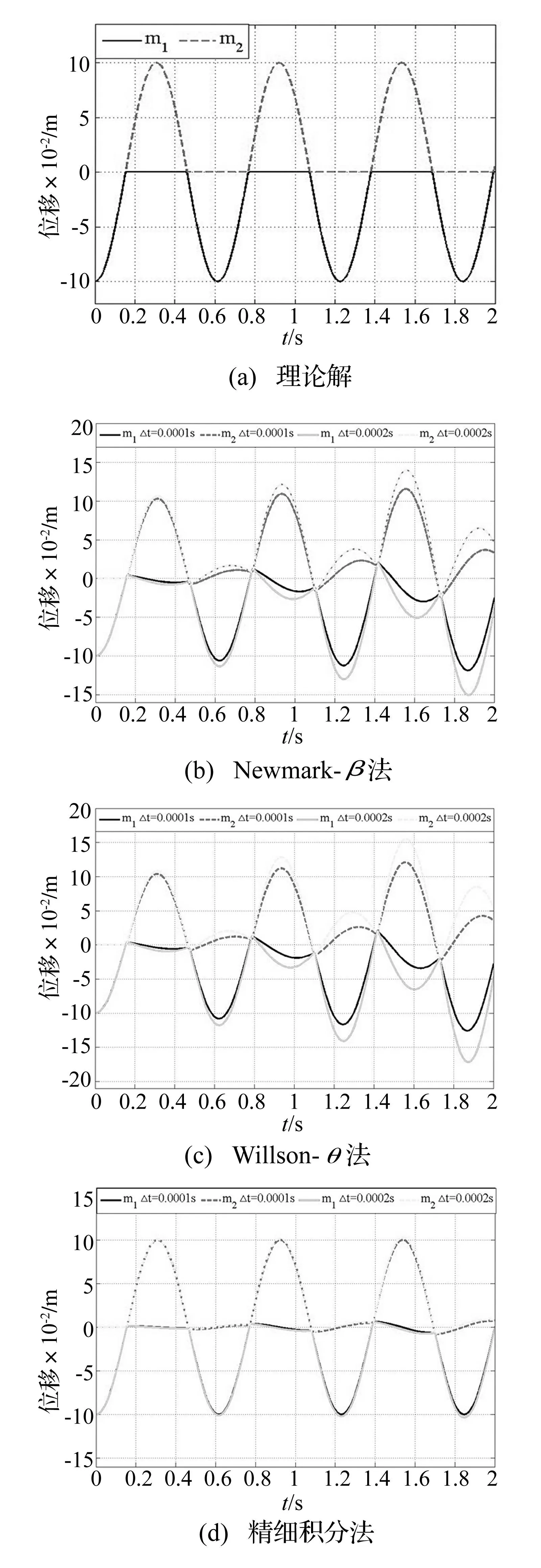
图2　质点位移响应 Fig.2 Displacement response of two masses

综上，精细积分法求解碰撞问题是有效的、实用的，由式(20)和式(21)知，精细积分法理论上可以实现任何精度。但由于碰撞过程短暂，采用精细积分法理论上宜选择较短的积分步长，这是由碰撞接触问题的特点和机理决定，而非精细积分法本身算法机理决定，根据本算例验证，在碰撞问题研究中选择积分步长0.000 2 s较为合适的，尤其利用精细积分法的稳定性特点，对于非撞击时刻可选择更大的积分步长，即变步长算法，可使计算效率大为提高。

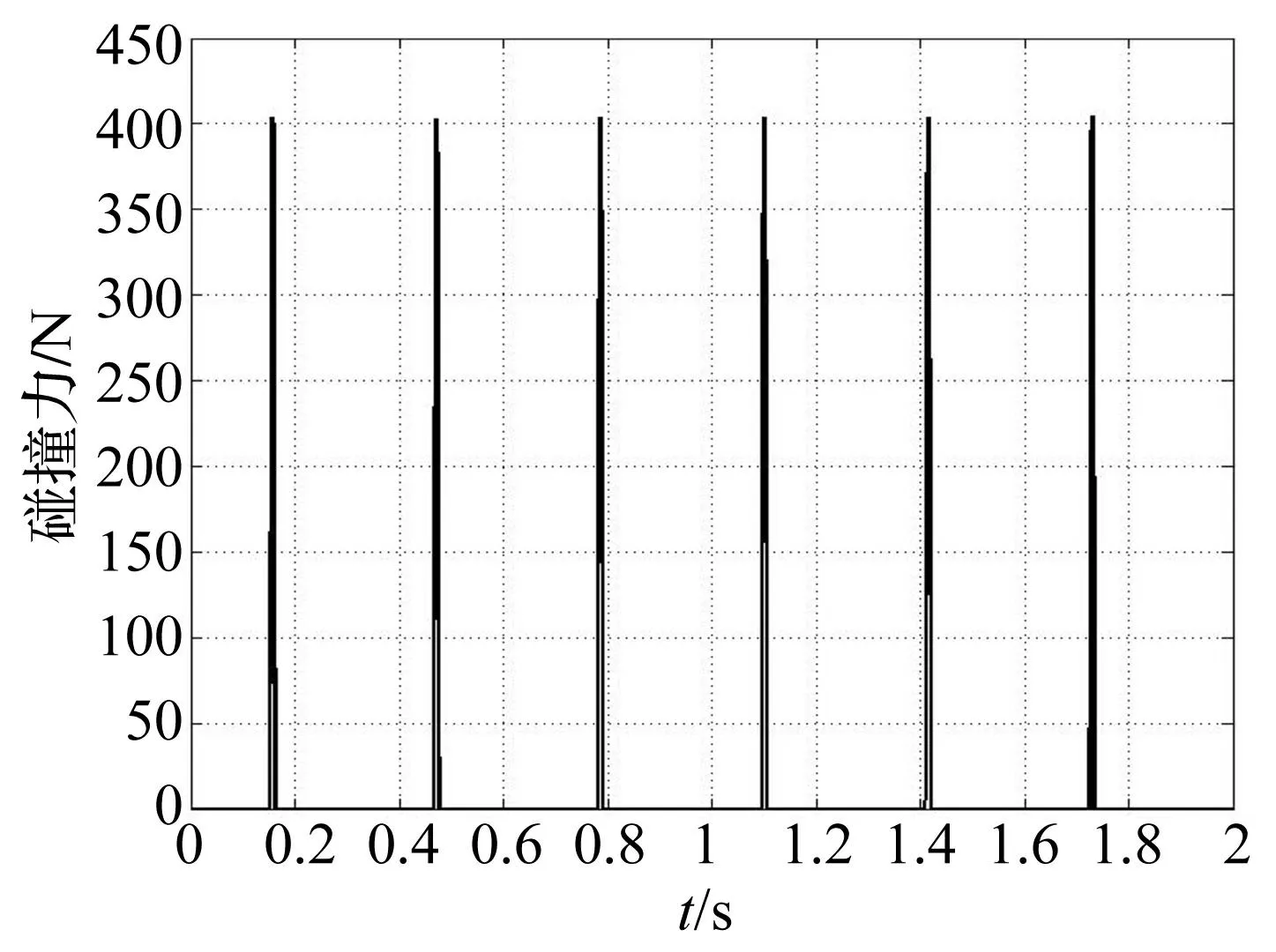
图3　基于精细积分法的碰撞力时程 Fig.3 Pounding force time history used precise integration method

3结构碰撞反应谱

(k=1,2)

(23)

基于精细积分法进行结构碰撞加速度反应谱曲线研究，图1中左侧为1#结构，右侧为2#结构，碰撞参数选取如下：

结构质量m1=m2=106kg，结构阻尼比ξ1=ξ2=0.05，初始间隙d=0.05 m，相邻结构的自振周期T1和T2为0.05～3 s，对应结构刚度k1和k2为4.39×106～1.58×1010N/m，周期间隔为 0.05 s。输入地震动采El-centro波(1940年，NS)，加速度峰值PGA=3.069 4 m/s2。

因碰撞结构是相邻两个单自由度体系，需要采用三维图形表示，为了更直观的观察对比，将结构无碰撞反应谱也表示为三维形式。

3.1阻尼比影响

图4给出相邻结构阻尼比相等且一致变化的碰撞加速度反应谱和无碰撞时的加速度反应谱；图5给出左侧结构阻尼比不变、 右侧结构阻尼比改变的碰撞加

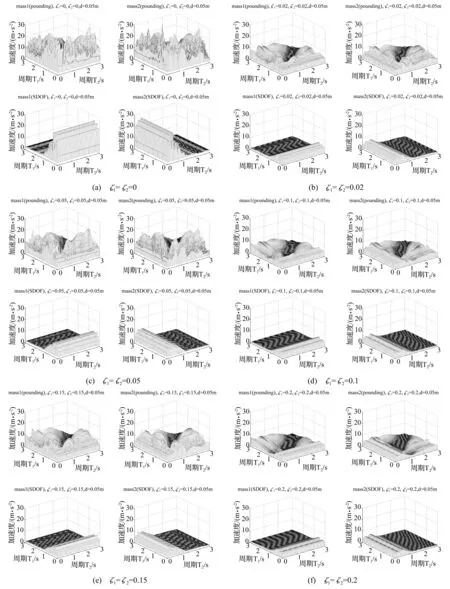
图4　x结构阻尼比ξ 1=ξ 2时的加速度反应谱 Fig.4 Acceleration spectra for different values of identical damping ratios, ξ 1= ξ 2, of both structures

速度反应谱和无碰撞时的加速度反应谱；以下左侧图为1#结构加速度反应谱，右侧图为2#结构加速度反应谱。表1给出不同阻尼比情况下的碰撞加速度谱峰值，可以看出，无碰撞情况下，加速度反应谱响应随着周期的增加而减小，碰撞发生时，这一现象不在存在；碰撞加大了结构的加速度响应，在结构阻尼比都为0.02时,2#结构的加速度响应增加幅值为120%；最大加速度响应对应的周期点也发生改变。随着阻尼比的增大，结构加速度响应增加幅度降低。

图5　1 #结构阻尼比ξ 1=0.05，2 #结构阻尼比ξ 2变化的加速度反应谱 Fig.5 Acceleration spectra for different values of damping ratio of 2 # structure ξ 2and constant value of damping ratio of 1 # structure ξ 1=0.05

由图4及表1，阻尼比在0～0.02范围时，2#结构因碰撞引起的加速度响应强于1#结构，阻尼比在0.02～0.2范围，2#结构的加速度响应则减弱，低于1#结构响应，总体差别在3%～26%。表明对于动力特性相同的两相邻结构，碰撞影响下产生的加速度响应有差异。由图5及表1，阻尼比差别越大，碰撞引起的加速度响应随之减小。

由图4～图5，对于碰撞结构，结构阻尼比的增大，使加速度响应为零的区域增加，此区域相邻结构的自振周期相当；增大阻尼比，结构不发生碰撞的区域增加，此区域结构碰撞反应谱与无碰撞反应谱形状一致。阻尼比在0～0.05范围时，碰撞加速度反应谱曲线多棱角和毛刺，在阻尼比为0.05～0.2范围，谱曲线逐渐转为圆滑，表明小阻尼结构受碰撞影响产生的响应较大阻尼结构强烈，因阻尼增加使结构的振动衰减加快，从而降低加速度响应，使谱曲线较为缓和。

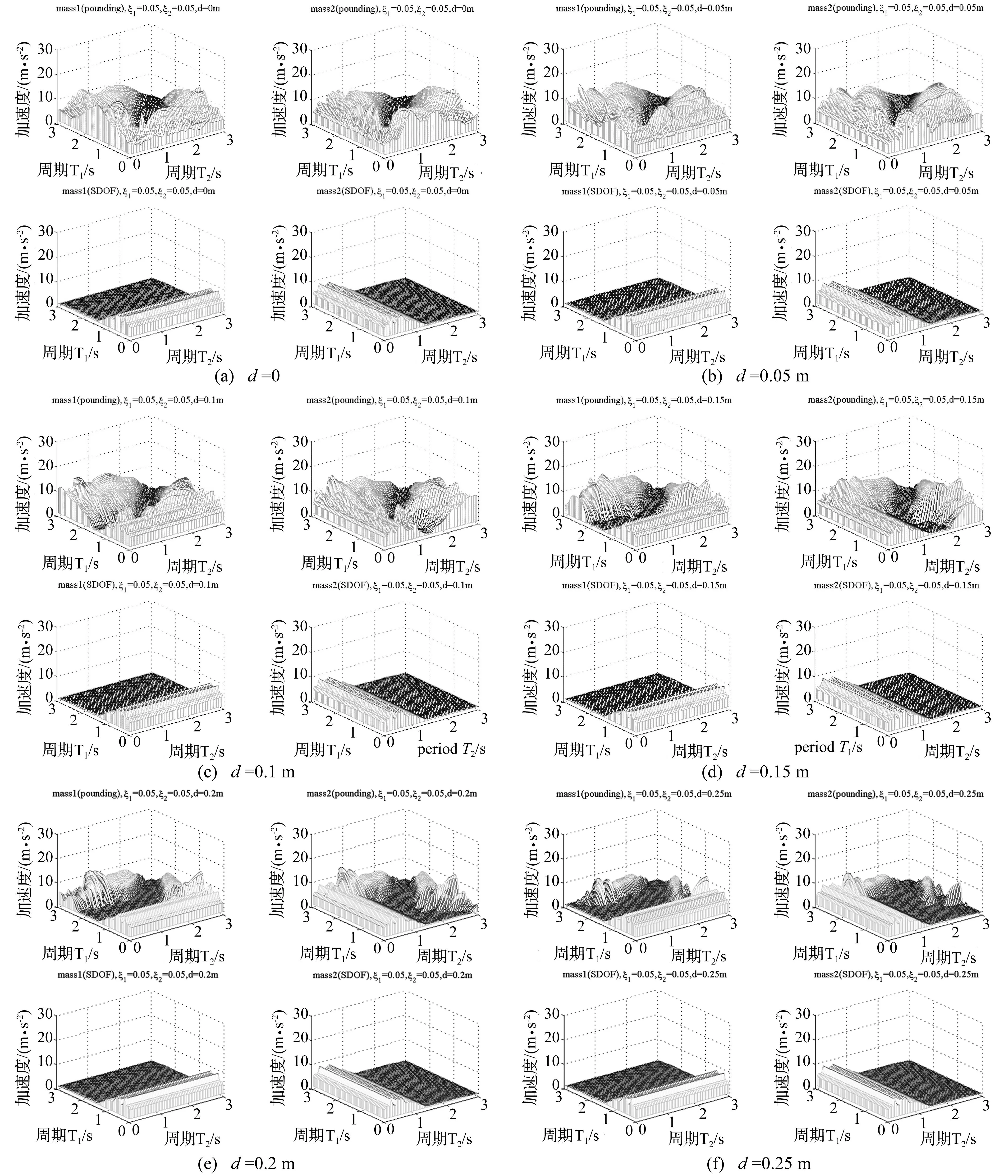
图6　不同间隙的碰撞加速度反应谱 Fig.6 Acceleration spectra for different values of gap size between structures

表1　碰撞加速度反应谱峰值(m/s 2)

3.2间隙影响

图6给出初始间隙不同的相邻结构加速度反应谱和无碰撞的加速度反应谱，表2给出碰撞加速度反应谱峰值。可以看出，碰撞加大了结构的加速度响应，在间隙为0.25 m时，碰撞使2#结构加速度响应增加47%。

随着间隙的逐渐增加，结构的加速度反应谱峰值有增有减，在间隙分别为0和0.25 m时，1#和2#结构碰撞加速度响应总体降低幅度都为31%，表明设置足够大的初始间隙可以减小结构的碰撞响应。间隙在00.15 m范围时，2#结构的加速度响应强于1#结构，间隙在0.20.25 m范围时，2#结构响应则弱于1#结构，总体1#和2#结构因碰撞引起的响应差别在07%，表明碰撞引起相邻结构的加速度响应有差异，间隙改变对这种差异的影响并不显著。

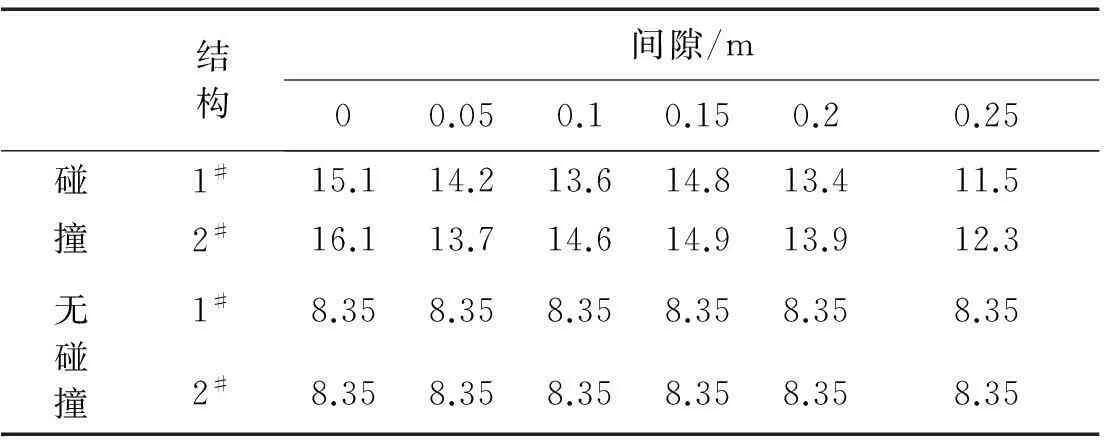
表2　碰撞加速度反应谱峰值(m/s 2)

由图6，间隙的增加，使结构碰撞反应谱曲线形状与无碰撞时完全一致的区域逐渐增加，在间隙增大时，这一现象尤其明显。在间隙在00.05m范围，阻尼比相等，相邻结构周期较小时时碰撞响应也相对较剧烈；间隙在0.10.2m范围，转为长周期时发生相对较大的加速度响应。

4结论

基于精细积分法对结构进行了碰撞加速度反应谱分析，精细积分法具有无条件稳定与高精度解的特点，应用于结构的碰撞响应分析中，提高计算效率和计算精度。主要结论如下：

(1) 精细积分方法理论上可实现任意精度，基于精细积分法推导的碰撞理论公式适宜于结构碰撞研究与应用。由于碰撞发生时间很短，精细积分法宜采用变步长以更快速的求解结构碰撞问题。但由积分步长选择产生的精度误差并非精细积分法本身造成的，而是由碰撞发生时间和机理决定。

(2) 碰撞会加大结构的加速度响应，响应大小与地震作用和结构动力特性有关；碰撞对动力特性相同的两相邻结构造成的响应有差异。阻尼比差别引起的相邻结构的加速度差异较为显著，间隙引起的响应差异则相对小一些。

(3) 相邻结构的阻尼比增大和阻尼比差别增加，在地震作用下因碰撞产生的加速度响应会降低。

(4) 若相邻结构设置足够的初始间隙，可减小结构碰撞的可能性和加速度响应。

参 考 文 献

[1] Kasai K, Maison B F. Building pounding damage during the 1989 Loma Prieta earthquake[J]. Engineering Structures,1997,19(3):195-207.

[2] Rosenblueth E, Meli R. The 1985 earthquake: causes and effects in Mexico City[M].1986.

[3] Newmark N M. A method of computation for structural dynamics[J]. Journal of Engineering Mechanics, 1959, 85(3): 249-260.

[4] Wilson E L, et al. Nonlinear dynamic analysis of complex structures[J]. Earthquake Engineering and Structural Dynamics, 1973, 1(3): 241-252.

[5] 钟万勰.结构动力方程的精细时程积分[J].大连理工大学学报，1994, 34(4): 131-136.

ZHONG Wan-xie. On precise time-intergration method for structural dynamics[J]. Journal of Dalian University of Technology, 1994, 34(4): 131-136.

[6] 钟万勰. 暂态历程的精细计算方法[J]. 计算结构力学及其应用, 1995, 12(1): 1-6.

ZHONG Wan-xie. Precise time-intergration method for the transient process[J]. Computational structural Mechanics and Applications, 1995, 12(1): 1-6.

[7] 钟万勰.计算结构力学与最优控制.[M].大连:大连理工大学出版社，1993.

[8] 克拉夫 R，彭津 J.结构动力学[M].王光远，译.北京：高等教育出版社,2006.

[9] Kawashima K, Sato T. Relative displacement response spectrum and its application[C]. In: Eleventh World Conference on Earthquake Engineering,1996.

[10] Ruangrassamee A, Kawashima K. Relative displacement response spectra with pounding effect[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(10): 1511-1538.

[11] 王君杰，喻志然.船撞设计冲击谱研究[J].振动与冲击,2014,33(14):11-14.

WANG Jun-jie,YU Zhi-ran.Design impact spectrum for vessel-bridge collision analysis[J].Journal of Vibration and Shock,2014,33(14):11-14.

[12] Jankowski R. Pounding force response spectrum under earthquake excitation[J].Engineering Structures,2006,28(8):1149-1161.

[13] Jankowski R. Non-linear viscoelastic modelling of earthquake‐induced structural pounding[J]. Earthquake Engineering & Structural Dynamics, 2005,34(6):595-611.

[14] 常春馨.现代控制理论基础[M].北京:机械工业出版社，1988.

[15] 胡聿贤.地震工程学[M].北京：地震出版社，2006.

[16] Mesguita C.Impacto entre Estruturas Adjacentes devido a Accao Sismica, M. Sc. dissertation[M]. Instituto Superisor Tecnico, Lisbon, Portugal，1991.

[17] Azevedo J, Bento R. Design criteria for buildings subjected to pounding[C]. Eleventh World Conference on Earthquake Engineering, Acapulco, Mexico, 1996.

[18] van Mier J G M, Pruijssers A F, Reinhardt H W, et al. Load-time response of colliding concrete bodies[J]. Journal of Structural Engineering, 1991, 117(2): 354-374.