基于 Bayes 法的电主轴极小子样可靠性研究

第一作者 蒋喜 男，硕士生，1987年生

通信作者 刘宏昭 男，教授，博士生导师，1954年生

基于Bayes法的电主轴极小子样可靠性研究

蒋喜, 刘宏昭，訾佼佼，原大宁，刘丽兰

(西安理工大学 机械与精密仪器工程学院，西安710048)

摘要：针对长寿命的磨削电主轴极小子样的可靠性评估问题，提出了Bayes结合虚拟增广样本的分析方法。首先，在Bayes法基本流程的指导下，研究了基于Bayes法的磨削电主轴可靠性评估方法。根据定时截尾试验的原则对电主轴进行可靠性试验，应用Bayes法结合磨削电主轴试验样本的可靠性试验数据，综合虚拟增广样本法对其可靠性进行评估，最终获得电主轴的可靠性评估结果。最后，将基于Bayes法与基于伪寿命分布法的磨削电主轴极小子样可靠性评估结果进行比较，以验证基于Bayes法可靠性评估理论的合理性。

关键词：电主轴；极小子样；Bayes；虚拟增广；可靠性

基金项目：国家科技重大专项计划资助项目(2010ZX04014-012)；国家自然科学基金(51275404)；陕西省自然科学基金(2012JQ7011)；陕西省重点学科建设专项资金资助项目

收稿日期：2013-10-21修改稿收到日期：2014-01-28

中图分类号:TH133.2文献标志码： A

Extremely small sample’s reliability of a motorized spindle based on Bayes method

JIANGXi,LIUHong-zhao,ZIJiao-jiao,YUANDa-ning,LIULi-lan(School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China)

Abstract:Aiming at the reliability evaluation of a long life grinding motorized spindle’s extremely small sample, a Bayes method combined with virtual augmented sample was proposed. Firstly, under the guidance of the basic process of Bayes method, the reliability evaluation method of a grinding motorized spindle based on Bayes method was studied. According to the principle of timing truncation tests, the reliability tests of the motorized spindle were conducted. Then, Bayes method combined with the reliability testing data of the grinding motorized spindle’s testings sample and the virtual augmented sample method was applied to assess the reliability of the spindle. Furthermore, the reliability evaluation results of the motorized spindle were obtained. Finally, the reliability evaluation results of the grinding motorized spindle based on Bayes method and those based on the false life’s distribution method were compared to verify the correctness of the proposed method.

Key words: motorized spindle; extremely small sample; Bayes; virtual augmented; reliability

磨削电主轴已较为普遍地被应用于数控加工中心，以实现机械加工的高速化和超精密化。作为数控加工中心的核心部件，磨削电主轴可靠性就成为了衡量整个数控加工中心可靠性的重要指标之一。对磨削电主轴的可靠性进行试验和评估，能够掌握其在实际使用过程中实现预定功能的能力，同时可以指导设计人员对其结构和相关参数进行改善，从而不断提高磨削电主轴的可靠性。由于电主轴属于高精度、长寿命、高可靠性产品，在短时间内对其进行可靠性试验难以获得失效寿命数据。因此，针对本课题涉及到的这类无故障情形下的磨削电主轴可靠性评估的问题，拟采用基于Bayes法的可靠性分析法进行研究。基于Bayes法的可靠性分析法是一种综合经验信息进行可靠性评估的方法[1]。该方法的特点在于先验分布，根据先验分布和试验数据导出后验分布，继而得到可靠性指标的贝叶斯推断，因此不需要很多的样本就能得到较好的估计。

近些年，国内外学者在这方面也取得了很多成果，使贝叶斯法得到了不断的改进和完善。如韩明[2]提出了产品无失效数据的一种“综合新Bayes估计法”。刘少刚等[3]针对舰船特种阀门可靠性评估比较困难的问题，提出了将Bayes理论和相似性理论相结合的评估新方法。此外，针对各类研究对象是小样本或者极小子样的情况，也有许多学者分别提出了不同的方法进行研究。如刘腾腾，刘建等[4]采用Bayes法结合最小二乘法来分析滚动轴承小样本无失效数据；冯蕴雯等[5]研究了在具有相同验前概率值的情况下,不同典型验前概率分布模型对做一次成功试验后所得的验后概率值的影响；曹浪等[6]研究了小样本情况下常见验前信息分布、验前信息的获取方法、验前信息的可信度确定，进而将Bayes法运用到性能退化模型的建立过程中。此外，文献[7-16]也对Bayes方法进行了深入地研究、拓展和应用。

此外，由于电主轴造价较高，使得试验成本较大，因此涉及到的电主轴样本只有两根。针对这类极小子样的可靠性研究，为了使电主轴可靠性评估结果的准确度更高，拟同时采用虚拟增广样本法将试验样本的截尾试验寿命进行虚拟扩展。在此基础上，对虚拟增广样本进行统计分析，以获得电主轴的一系列可靠性指标。因此，应用本方法对磨削电主轴进行可靠性评估，既缩短了磨削电主轴可靠性试验时间，又使得最终的评估结果不失精确性。

1Bayes法的基本流程

对于试验样本的可靠性数据所服从的分布函数中的未知参数θ，应用Bayes法进行估计的基本流程如下：

(1) 根据未知参数θ的先验信息确定θ的先验分布π(θ)。

(2) 确定依赖于未知参数θ的密度函数p(x|θ)。该函数表示在随机变量θ给定某个值时，总体指标X的条件分布。根据贝叶斯观点，可得密度函数p(x|θ)为：

(1)

此函数亦称为似然函数，记为L(θ)。

(3) 由先验分布π(θ)和密度函数p(x|θ)可得到样本x和参数θ的联合分布为：

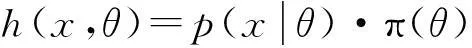
(2)

(4) 推断未知参数θ的后验分布。先将h(x,θ)分解为：

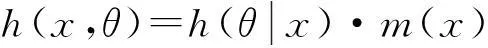
(3)

式中:m(x)是x的边际密度函数，其表达式为：

(4)

由式(4)可知m(x)中不含θ的任何信息，其中Θ是θ的取值空间。因此只能用条件分布h(θ|x)来对θ作出统计推断，其计算表达式为：

(5)

式(5)即为贝叶斯公式的密度函数形式。

在样本x给定下，θ的条件分布h(θ|x)被称为θ的后验分布，其包含了总体、样本和先验等三种信息中有关未知参数θ的所有信息，同时又排除了所有与θ无关的信息[17-19]，所以基于后验分布h(θ|x)对θ进行统计推断比基于先验分布的推断更为有效、更为合理。

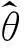
2基于Bayes法的电主轴可靠性评估

2.1理论研究

由于迄今为止对于磨削电主轴的可靠性试验不够普遍，开展的相关工作也不是非常的系统，因此人们对于电主轴的失效所应服从的分布也不是很明确。鉴于这种情形，我们致力于在整个电主轴单元中寻求一些对于电主轴综合性能影响较大的典型零部件，并且该部件在工程中的可靠性试验应已经较为完善和普遍，其失效所服从的分布也应较为明确。在此基础上，可将该典型零部件的失效分布函数近似代替电主轴的失效分布函数。

在该思想的指导下，电主轴的支承轴承的磨损及疲劳剥落等形式的失效对于电主轴的综合性能(如电主轴的轴端跳动和主轴振动等)影响较大，也较直接，同时对于轴承的研究技术已发展得较为成熟，部分企业和科研院校都对其开展过长期的可靠性试验，对所获得的大量试验数据的分析可获知其失效所服从的分布为威布尔分布函数。因此我们最终选择威布尔分布函数来近似代替电主轴的失效分布函数。

针对本研究对象的实际状况，推断威布尔分布的Bayes分析方法：

两参数威布尔分布的分布函数为：

(6)

令：λ=(1/η)m，则式(6)转化为：

F(t)=1-exp(-λtm)

(7)

对于参数λ，可选择伽玛分布Γ(σ,τ)作为其共轭先验分布；对于参数m则没有共轭先验分布，由于电主轴属于高可靠性、长寿命产品，因此其失效率是递增的，即m>1,此时可令m1=m-1,则可取m1的先验分布为伽玛分布Γ(α,β)。又因为λ和m1是相互独立的，因此可得λ和m1的先验分布为：

(8)

由于涉及到的研究对象——电主轴属于高可靠性产品，在短时间内很难得到失效寿命数据，因此专门在无失效寿命数据的条件下进行研究。在无失效情形下，相应的似然函数为：

(9)

式中:t1,t2,…,tn指的是对n个试验样品逐个进行定时截尾试验的截尾试验时间。

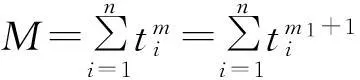
L(λ,m1)=e-λM

(10)

于是可得样本t1,…,tn和参数λ、m1的联合分布h(t1,…,tn|λ,m1)为：

h(t1,…,tn|λ,m1)=L(λ,m1)·π(λ,m1)=

(11)

将式(11)代入式(5)可得λ和m1的联合后验分布h(λ,m1|t1,…,tn)为：

(12)

由式(12)可得到m1的后验分布为：

(13)

而λ的后验分布为：

(14)

(15)

(16)

(17)

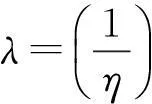
(18)

2.2磨削电主轴可靠性试验及评估

2.2.1试验设备及原理[20]

采用逐次定时截尾试验的可靠性试验方法，且均在主轴转速为8 000 r/min，轴端径向载荷为80 N的试验条件下，对两根磨削电主轴进行可靠性试验，其主要试验设备见图1。

1. 振动速度传感器　2. 激光位移传感器感测头 3.离心式风机　4. 恒流源　5.加载盘 6. 电磁加载装置　7. 磨削电主轴 图1　电主轴实验设备 Fig.1 The electric spindle test equipment

该试验平台的主要工作原理是：在接通所有设备电源之后，先启动水冷机给电主轴通循环冷却水，再通过调节变频器控制电主轴的转速达到8 000 r/min，接着启动恒流源给电磁加载装置供电，以实现对电主轴轴端加载盘施加电磁力，并根据磨削电主轴的载荷谱控制电磁加载力的大小，由此模拟电主轴在实际磨削加工过程中的磨削力。然后，在电主轴运行稳定后，每隔一段时间通过激光位移传感器和振动速度传感器分别测量电主轴轴端径向跳动量和振动速度值，检查各项指标是否超过允许值。在截尾试验时间内，若各指标均未超出允许值，则试验至设定的截尾时间时停止试验；若某指标超出允许值，则即刻终止试验。

2.2.2磨削电主轴可靠性评估

在开展整个试验前，将两个试验样品逐个进行定时截尾试验的截尾试验时间分别设定为955 h、1 452 h，最终各试验样品在各自的可靠性截尾试验时间内均未出现失效。在此基础上，首先根据虚拟增广样本法的基本原理，即虚拟增广后的虚拟样本的均值应与原始试验样本的均值相等，而且其标准差应与类似件的样本标准差相等[21]，选取虚拟增广样本数为13，即将原始的2个扩展为13个。根据威布尔分布密度函数的偏态性，可得截尾试验寿命的虚拟增广样本为T1=120.35 h，T2=361.05 h，T3=481.40 h，T4=601.75 h，T5=722.10 h，T6=842.45 h，T7=962.80 h，T8=1 083.2h，T9=1 203.5 h，T10=1 444.2 h，T11=1 684.9 h，T12=1 925.6 h，T13=2 482 h。

然后采用“2.1’所阐述的理论对磨削电主轴的可靠性进行评估，具体过程如下：

由文献[22]可知球轴承的形状参数一般取为1.5，因此拟取电主轴的疲劳失效寿命所符合的威布尔分布形状参数m的初值为1.5。在此基础上，结合文献[1]介绍的先验分布中超参数的确定方法，确定m1(m1=m-1)的先验分布——伽玛分布Γ(α,β)和λ的先验分布——伽玛分布Γ(σ,τ)中的超参数α，β，σ和τ。

根据先验信息只能获得m1的先验均值为：

(19)

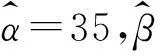
由于本研究的磨削电主轴的应用场合是数控加工中心或者数控磨床，对于此类应用场合而言，电主轴的主要失效形式是加工精度的丧失，而不是其内部材料的疲劳失效。而相对疲劳失效的寿命而言，加工精度的丧失失效寿命较短，并且很难精确获得。此外，精度寿命与电主轴的实际工况和用户的维护情况关系较大。因此，考虑到所研究的磨削电主轴的实际状况，结合蒋喜等[20]的分析结果，初选电主轴的特征寿命为2 500h，即威布尔分布中的真尺度参数η=2 500，则参数λ的先验均值为：

(20)

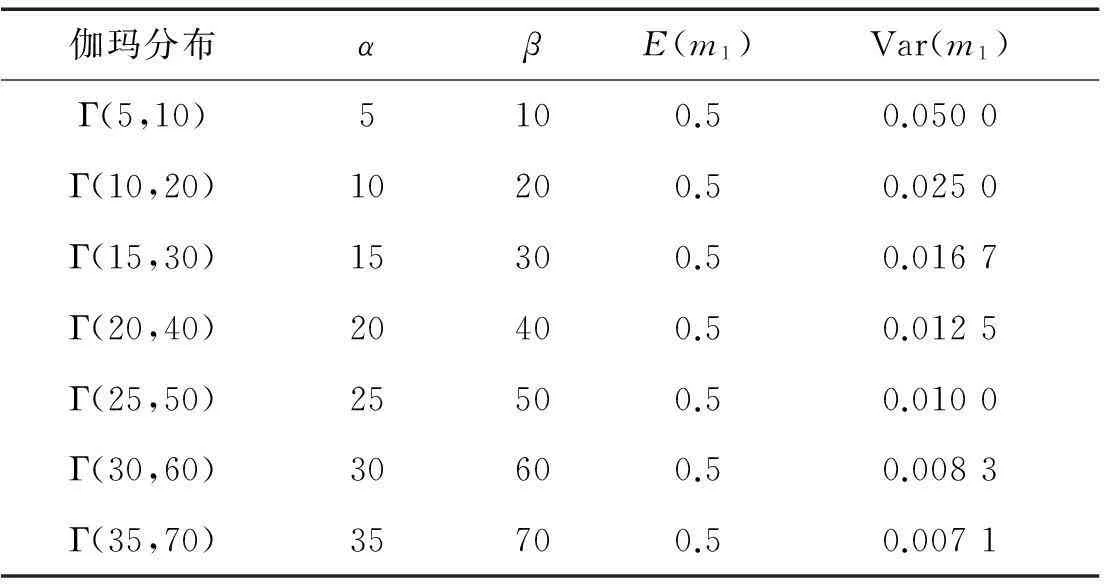
表1　伽玛分布Γ(α,β)中超参数与方差的关系

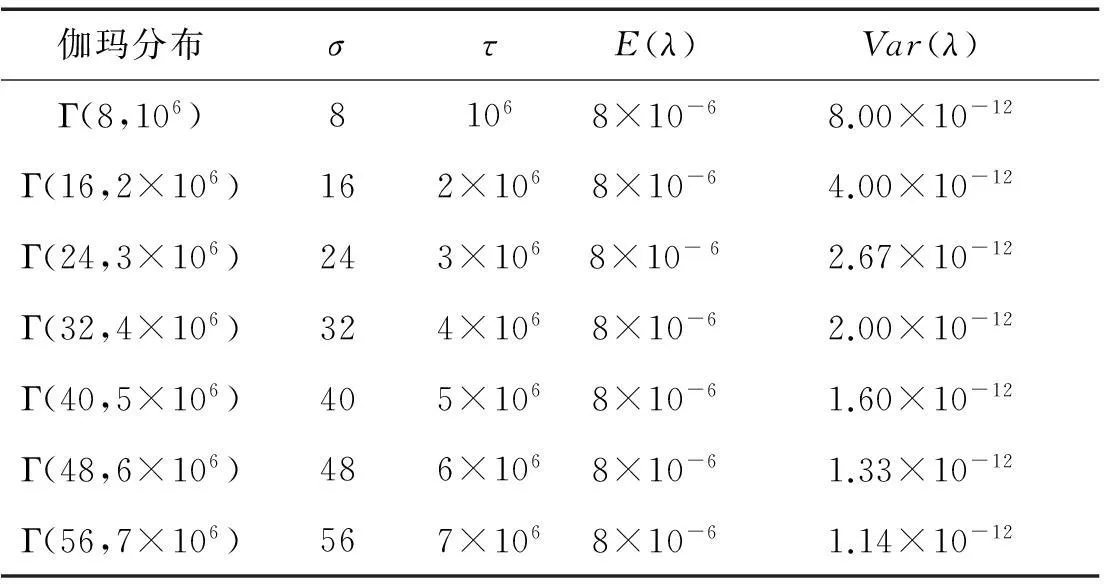
表2　伽玛分布Γ(σ,τ)中超参数与方差的关系

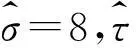
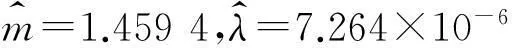
由Bayes法所获得的磨削电主轴可靠度函数曲线可知：随着磨削电主轴使用时间的延长，磨削电主轴的可靠度也随之不断降低。

(21)

将上述相关参数的贝叶斯估计值分别代入两参数威布尔分布的相关函数表达式，可得磨削电主轴的可靠性指标如下：

(1) 平均寿命的估计值E(T)为：

(22)

(2) 失效分布函数F(t)和分布密度函数f(t)分别为:

1-exp(-7.264×10-6×t1.459 4)

(23)

(24)

则由式(24)可得磨削电主轴的失效分布密度函数曲线，如图3所示。同时可得，当t≈1 510 h时，f(t)max=2.230 2×10-4。这表示在本课题设定的工况下，该型号电主轴的试验样本中大约运行到1 510h时失效的个体总数占整个试验样本的比例是最大的，约为0.022 3%。

(3) 由上述分析易得，电主轴的可靠度函数为：

(4) 电主轴失效率函数为：

(26)

由此可得电主轴失效率函数曲线如图4所示。

由图4可知：磨削电主轴的失效率函数为递增型，在运行约8 000h的时候，其失效率达到6.585 2×10-4(个)/h，该值表示每10 000根该型号磨削电主轴在本课题设定的工况下工作8 000h后只有约7根电主轴失效。而在此时间点之前，各个时刻电主轴的失效率均低于6.585 2×10-4(个)/h。由此可见，该电主轴的可靠性较高。

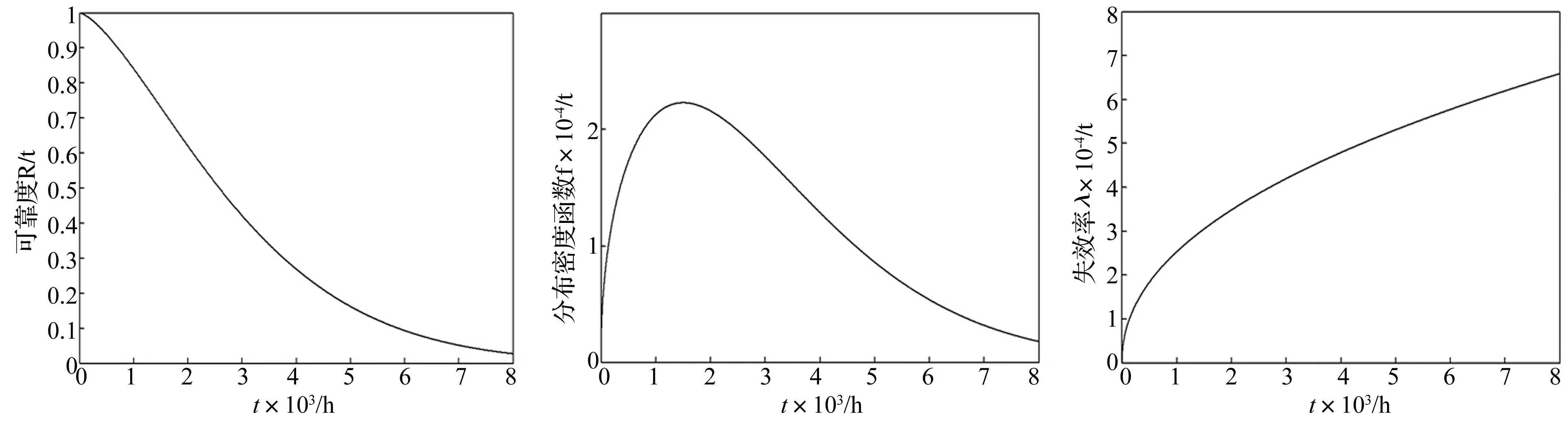
图2 磨削电主轴可靠度函数曲线Fig.2Reliabilityfunctioncurveofgrindingmotorizedspindle图3 磨削电主轴分布密度函数曲线Fig.3Distributiondensityfunctioncurveofgrindingmotorizedspindle图4 磨削电主轴失效率函数曲线Fig.4Failureratefunctioncurveofgrindingmotorizedspindle

(5) 该电主轴的可靠寿命为：

(27)

则其中位寿命为：

(28)

特征寿命为：

(29)

3评估结果的比较

采用Bayes法结合虚拟增广样本法对磨削电主轴极小子样的可靠性进行评估，将其评估结果与蒋喜[20]采用基于伪寿命分布法结合虚拟增广样本法的磨削电主轴极小子样可靠性评估方法的评估结果进行比较，各个可靠性指标的对比图表分别见图5～图7和表3。

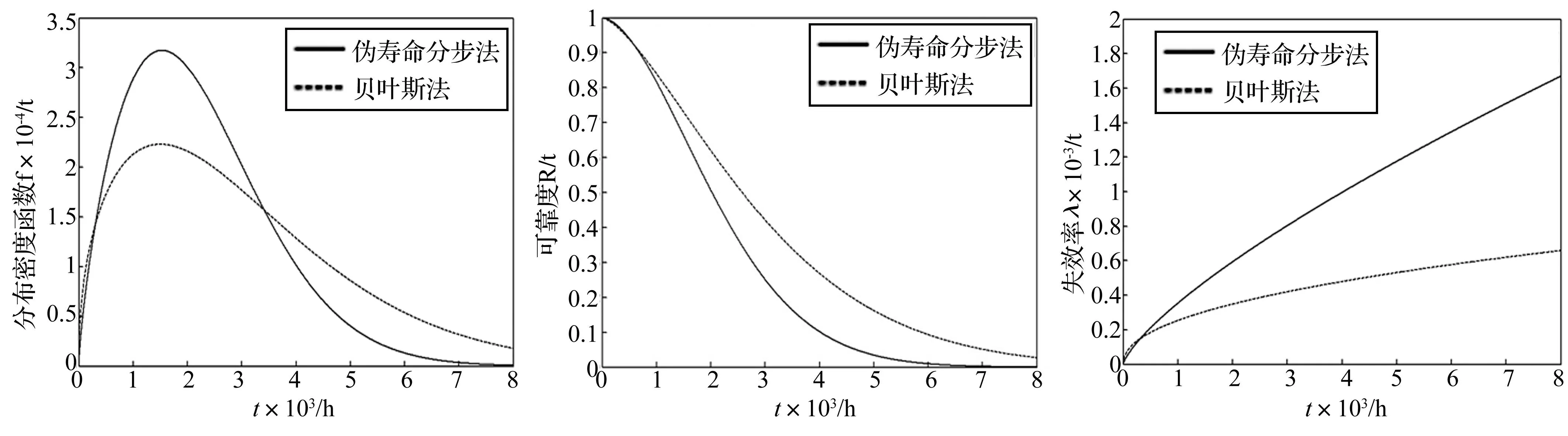
图5 磨削电主轴的分布密度函数曲线对比图Fig.5Contrastingofdistributiondensityfunctioncurveofgrindingmotorizedspindle图6 磨削电主轴的可靠度函数曲线对比图Fig.6Contrastingofreliabilityfunctioncurveofgrindingmotorizedspindle图7 磨削电主轴的失效率函数曲线对比图Fig.7ContrastingofFailureratefunctioncurveofgrindingmotorizedspindle

表3　磨削电主轴部分可靠性指标汇总表

由图5～图7及表3易知：由两种不同可靠性评估方法获得的关于磨削电主轴的一系列可靠性指标不同，存在一定的差异。造成这种差异主要是因为影响上述两种方法分析结果的因素不同，伪寿命分布法的主要影响因素是退化轨迹模型的选取和失效阈值的确定，Bayes法的主要影响因素是先验分布的确定以及先验分布中超参数的确定。其中失效阈值的确定主要是由电主轴在实际工况下所需达到的加工精度等条件决定的，而先验分布是根据经验和历史资料来确定的。

对于本课题的研究对象而言，由于其可靠性指标暂无统一的标准，因此无法衡量两种可靠性评估方法的优劣。但其中两者的分布密度函数、可靠度函数和失效率函数的变化趋势基本一致，在一定范围内也处于同一数量级的水平，并且两者的平均寿命、中位寿命及特征寿命等指标也较为接近，因而在一定程度上体现出两种可靠性评估方法对磨削电主轴的可靠性进行评估均有一定的合理性。

4结论

针对采用传统基于寿命数据的可靠性分析方法对磨削电主轴的可靠性进行评估较为困难的问题，提出了将Bayes与虚拟增广样本相结合的可靠性分析方法来解决磨削电主轴的极小子样可靠性问题，主要研究工作为：

(1) 研究了Bayes法的基本原理和流程，并对基于Bayes法的磨削电主轴可靠性评估方法进行了理论分析。

(2) 结合磨削电主轴试验数据，应用基于Bayes法的磨削电主轴可靠性分析方法对磨削电主轴进行可靠性评估，获得一系列可靠性指标。

(3) 将基于Bayes法的磨削电主轴极小子样可靠性评估结果与基于伪寿命分布法的磨削电主轴极小子样可靠性评估结果进行比较，以验证本文研究的合理性。

评估结果表明，该电主轴的可靠度随时间的变化趋势基本符合机械产品的性能退化规律，同时其平均失效寿命基本符合正常工况下的一般范围。

参 考 文 献

[1] 赵宇.可靠性数据分析[M].北京：国防工业出版社，2011.

[2] 韩明.产品无失效数据的综合处理[J].机械工程学报，2003,39(2):129-132.

HAN Ming. Synthesized process for zero-failure data of the products[J].Journal of Mechanical Engineering，2003,39(2):129-132.

[3] 刘少刚，李少杰，舒海生，等.小子样状态下舰船特种阀门可靠性评估方法研究[J].哈尔滨工程大学学报, 2012,33(4):1-5.

LIU Shao-gang，LI Shao-jie，SHU Hai-sheng,et al. Research on reliability assessment of vessel special valve in small sample condition[J].Journal of Harbin Engineering University, 2012,33(4):1-5.

[4] 刘腾腾,刘建亭,崔凤奎,等.滚动轴承小样本无失效数据的Bayes可靠性分析[J].河南科技大学学报,2009,30(6):20-22.

LIU Teng-teng，LIU Jian-ting，CUI Feng-Kui,et al. Reliability analysis about small sample zero failure data of rolling bearing[J].Journal of Henan University of Science and Technology,2009,30(6):20-22.

[5] 冯蕴雯,冯元生.极小子样高可靠性成败型产品试验的贝叶斯评估方法研究[J].机械科学与技术,1999,18(2): 198-200.

FENG Yun-weng, FENG Yuan-sheng. Study of Bayes’ estimation for product test of extreme small-sample high-reliability safe-or-failure pattern[J].Mechanical Science and Technology,1999,18(2): 198-200.

[6] 曹浪,李银军,李献锋,等. 基于小样本Bayes理论的可靠性评估方法[J].电子质量,2010(10):25-27.

CAO Lang，LI Yin-jun，LI Xian-feng,et al. Research on reliability evaluation method based on Bayes theory of small-sample[J].Electronic Quality,2010(10):25-27.

[7] 张晓冉,胡文杰,夏茂辉.分组定时截尾无失效数据的迭代Bayes分析[J].工程数学学报,2009,26(2): 267-272.

ZHANG Xiao-ran, HU Wen-jie, XIA Mao-hui. Iterative bayes analysis of the grouped, timing terminated and zero-failure data[J].Chinese Journal of Engineering Mathematics,2009,26(2): 267-272.

[8] Wu H C. Bayesian system reliability assessment under fuzzy environments[J].Reliability Engineering & System Safety,2004,83(3):277-286.

[9] Sarhan A. Non-parametric empirical Bayes procedure[J].Reliability Engineering & System Safety, 2003,80(2):115-122.

[10] Taheri S M，Zarei R. Bayesian system reliability assessment under the vague environment[J].Applied Soft Computing,2011,11(2):1614-1622.

[11] 刘永峰,郑海鹰.无失效数据的统计分析[J].浙江大学学报:理学版,2012,39(3):273-277.

LIU Yong-feng，ZHENG Hai-ying. Statistical analysis about zero-failure data[J].Journal of Zhejiang University：Science Edition,2012,39(3):273-277.

[12] 韩芳,钟冬望,汪君.基于贝叶斯法的复杂有限元模型修正研究[J].振动与冲击,2012,31(1):39-43.

HAN Fang，ZHONG Dong-wang，WANG Jun. Complicated finite element model updating based on Bayesian method [J]. Journal of Vibration and Shock, 2012,31(1):39-43.

[13] 郝腾飞,陈果.基于贝叶斯最优核判别分析的机械故障诊断[J].振动与冲击,2012,31(13):26-30.

HAO Teng-fei，CHEN Guo. Machinery fault diagnosis based on Bayes optimal kernel discriminant analysis[J].Journal of Vibration and Shock,2012,31(13): 26-30.

[14] 邱金水,李少杰,刘少刚,等.舰船特种阀门极少失效条件下可靠性寿命研究[J].哈尔滨工程大学学报,2012,33(9):1086-1090.

QIU Jin-shui，LI Shao-jie，LIU Shao-gang,et al. Research on the reliability life of a vessel special valve based on few-failure data[J].Journal of Harbin Engineering University,2012,33(9):1086-1090.

[15] 张建军,谢敬芝,刘征宇. 基于置信分布和K-L信息距离的成败型产品可靠性分析[J].电子测量与仪器学报,2011,25(4):320-324.

ZHANG Jian-jun，XIE Jing-zhi，LIU Zheng-yu. Bayesian analysis for reliability of success-failure products based on confidence distribution and K-L information distance[J].Journal of Electronic Measurement and Instrument, 2011,25(4):320-324.

[16] 陈振珩,刘雨时. 基于 Bayes 可靠性评估验前信息检验方法的研究[J].电子测量与仪器学报,2008(S1):41-44.

CHEN Zhen-heng，LIU Yu-shi. Test method of prior information based on bayes reliability evaluation[J].Journal of Electronic Measurement and Instrument,2008(S1):41-44.

[17] 马彦辉.基于GLM的非正态响应稳健设计研究[D].天津：天津大学,2008.

[18] 孟利锋.随机波动模型及其建模方法研究[D].天津：天津大学,2004.

[19] 任枫.非对称双指数跳跃扩散模型的贝叶斯分析[D].天津：天津大学,2007.

[20] 蒋喜,刘宏昭,刘丽兰,等.基于伪寿命分布的电主轴极小子样可靠性研究[J].振动与冲击,2013,32(19):80-85.

JIANG Xi，LIU Hong-zhao，LIU Li-lan，et al. Research on extremely small-scale sample’s reliability of electric spindle based on distribution of false life[J].Journal of Vibration and Shock,2013,32(19):80-85.

[21] 黄玮，冯蕴雯，吕震宙.极小子样实验的虚拟增广样本评估方法[J].西北工业大学学报，2005，23( 3)： 384-387．

HUANG Wei，FENG Yun-wen，LÜ Zhen-zhou. Virtually expanded sample estimation method for extremely small-scale sample test[J].Journal of Northwestern Polytechnical University，2005，23(3)： 384-387．

[22] 杨晓蔚. 滚动轴承疲劳寿命威布尔分布三参数的研究[D].合肥：合肥工业大学,2003.