滚球型准零刚度隔振器的特性分析

第一作者 王毅 男，硕士，1988年生

通信作者 徐道临 男，博士，教授，1958年生

邮箱：dlxu@hnu.edu.cn

滚球型准零刚度隔振器的特性分析

王毅，徐道临，周加喜

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙410082)

摘要：针对工程实践中的低频隔振难题，提出一种紧凑的、带滚球装置的准零刚度隔振器。首先，对隔振器进行了静力学分析，得到了实现准零刚度的参数条件；其次，建立了隔振系统动力学模型，利用谐波平衡法分析了系统频响特性及隔振性能，讨论了激励幅值和阻尼对响应的影响；最后，利用ADAMS对系统动力学特性进行仿真及隔振效果评估。结果表明，与相应的线性隔振系统相比，准零刚度隔振器的起始隔振频率显著降低，且在低频范围内力传递率比线性系统低得多。因此，滚球装置提供的负刚度明显降低了系统竖向总刚度，使系统具有优异的低频隔振性能，更重要的是紧凑的设计使其更易工程化。

关键词：滚球型隔振器；准零刚度；低频隔振

基金项目：国家自然科学

收稿日期：2013-11-01修改稿收到日期：2014-02-25

中图分类号:O328文献标志码： A

Characteristic analysis of a ball-type vibration isolator with quasi-zero-stiffness

WANGYi,XUDao-lin,ZHOUJia-xi(State Key Laboratory of Adraced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China)

Abstract:A compact ball-type quasi-zero-stiffness (QZS) vibration isolator was proposed for the purpose of low-frequency vibration isolation. Firstly, its parameters of quasi-zero stiffness were obtained using a static analysis. Furthermore, the dynamic model of the vibration isolation system was established, and the frequency-response characteristic and vibration isolation performance were analyzed with the harmonic balance method. The effects of excitation amplitude and damping on the system response were also discussed. Finally, numerical simulations were performed with ADAMS software, and the vibration isolation effects were evaluated. The results showed that compared with the corresponding linear vibration isolation system, the QZS vibration isolator can obviously reduce the starting vibration isolation frequency, and has a much lower load transmissibility in the range of low frequency; therefore, the negative stiffness provided by the ball-type mechanism significantly reduces the total vertical stiffness of the system, and the excellent low-frequency vibration isolation performance is achieved; what’s more, its compact design makes it more convinient to be used in engineering.

Key words: ball-type vibration isolator; quasi-zero-stiffness; low-frequency vibration isolation

近年来，隔振技术愈来愈受到人们的重视，人们对振动环境、产品与结构振动特性的要求进一步提高，比如测量时光学隔振平台对高精密光学仪器的隔振保护、水下航行潜艇的减振降噪等，都对隔振技术的要求越来越严格。主要基于两方面的原因：一方面，我们生活中的振源强度在日益加大，例如，机械设备运转速度剧增、越野汽车和内燃机数量不断增加等；另一方面，工程技术中对振级的限制要求愈来愈严格[1]。

目前，现有的准零刚度隔振器，在实验中都证明，其隔振性能依赖于其振动幅值，只有在某个大振幅振动状态下，才能表现出其优良的隔振性能[6]。若被隔振设备静平衡位置微幅振动，如1 mm甚至0.1 mm的振幅，则达不到预期的隔振效果。初步分析其原因是，微幅振动时，由于斜弹簧摆角太小，负刚度机构未起作用。采用直径非常小的滚球机构代替斜弹簧，当产生微幅振动时，负刚度机构能充分参与其中。进一步对隔振器进行静力学分析，设计系统参数，实现准零刚度。然后，建立个隔振系统动力学模型，并用谐波平衡法进行近似求解，并评估系统的隔振性能。最后，利用Adams对系统进行动力学仿真分析，验证系统优异的隔振性能。

1静力分析

1.1设计原理

滚球型准零刚度隔振器(见图1),由底座、上盖和连接件组成，核心部件包括具有负刚度的水平弹性件、具有正刚度的竖直弹性件及以水平中心面对齐方式始终保持接触的滚球接触副，此接触副包括内滚球和外滚球机构，两个外滚球始终在水平方向运动，两个内滚球始终在竖直方向运动，滚球的直径均小于1 cm。水平弹性件设置在一水平调节机构内，外滚球连接水平调节机构，内滚球连接水平振动台，水平振动台由竖直弹性件支撑，竖直弹性件连接一竖直调节机构，然后连接到底座。

如图1(a)和图1(b)，当激振力作用在水平振动台“4”时，外滚球“14”沿竖直方向上下振动，通过滚球副驱使内滚球“13”水平方向振动，激振力通过水平弹性件和竖直弹性件传递到底座上。设计滚球副是为了增加隔振时对小位移的敏感性，具体是通过设计两对滚球副，使水平弹性件作用在振动体上的力矢量摆角增大，从而增加对微幅振动的负刚度敏感性，进而实现微幅振动的准零刚度隔振。

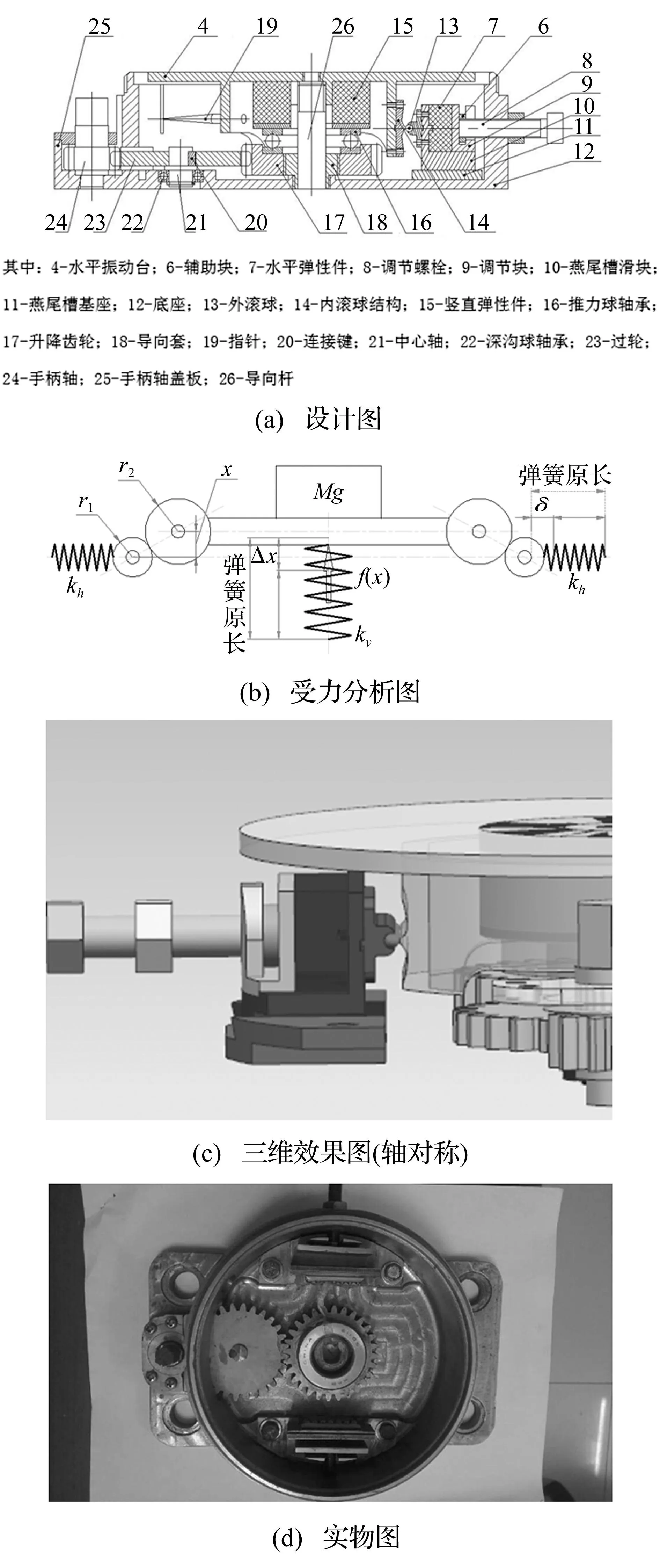
图1　滚球型准零刚度隔振器 Fig.1 Ball-type quasi-zero-stiffness isolator

1.2静力学分析

竖弹簧的刚度为kv，水平弹簧的刚度为kh。两个滚轮的半径分别为r1，r2。处于静平衡位置时，竖弹簧的压缩量为Δx=Mg/kv，水平弹簧的压缩量为δ。如图1(b)，在竖直向上的力f(x)的作用下，质量向上位移x，f(x)与x的关系为:

(1)

系统刚度为:

准零刚度条件:

(3)

即

(4)

满足准零刚度条件的力与位移关系

(5)

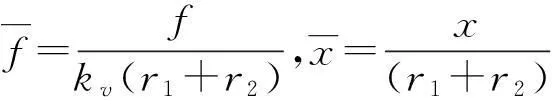
(6)

满足准零刚度条件的系统刚度为：

(7)

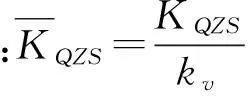
(8)

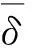
(9)

图2　准零系统无量纲刚度 Fig.2 Quasi-zero-system dimensionless stiffness

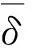
2动力学分析

建立系统的运动方程

(10)

式中：F0和ω分别为激励的幅值和频率。将式(5)代入式(10)得

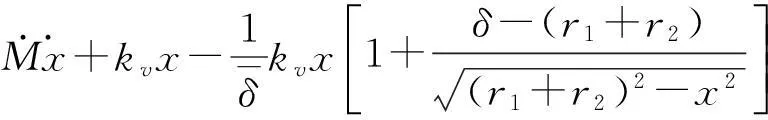
(11)

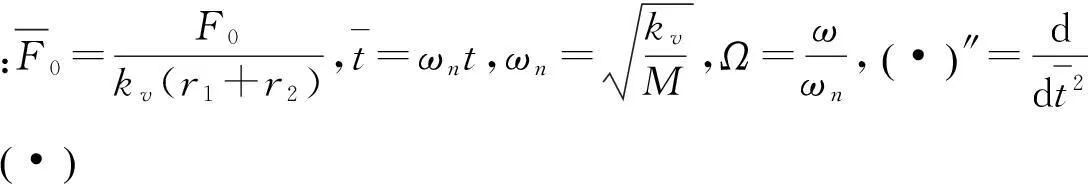
(12)

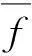
(13)

加入适当阻尼后系统运动方程可写为：

(14)

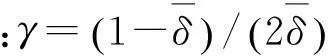
利用谐波平衡法可得系统稳态响应幅值与频率之间的近似关系为：

(15)

系统的跳跃频率可近似地表示为：

(16)

当系统响应由一阶谐波主导时，系统的力传递率可近似表示为：

(17)

3算例

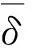
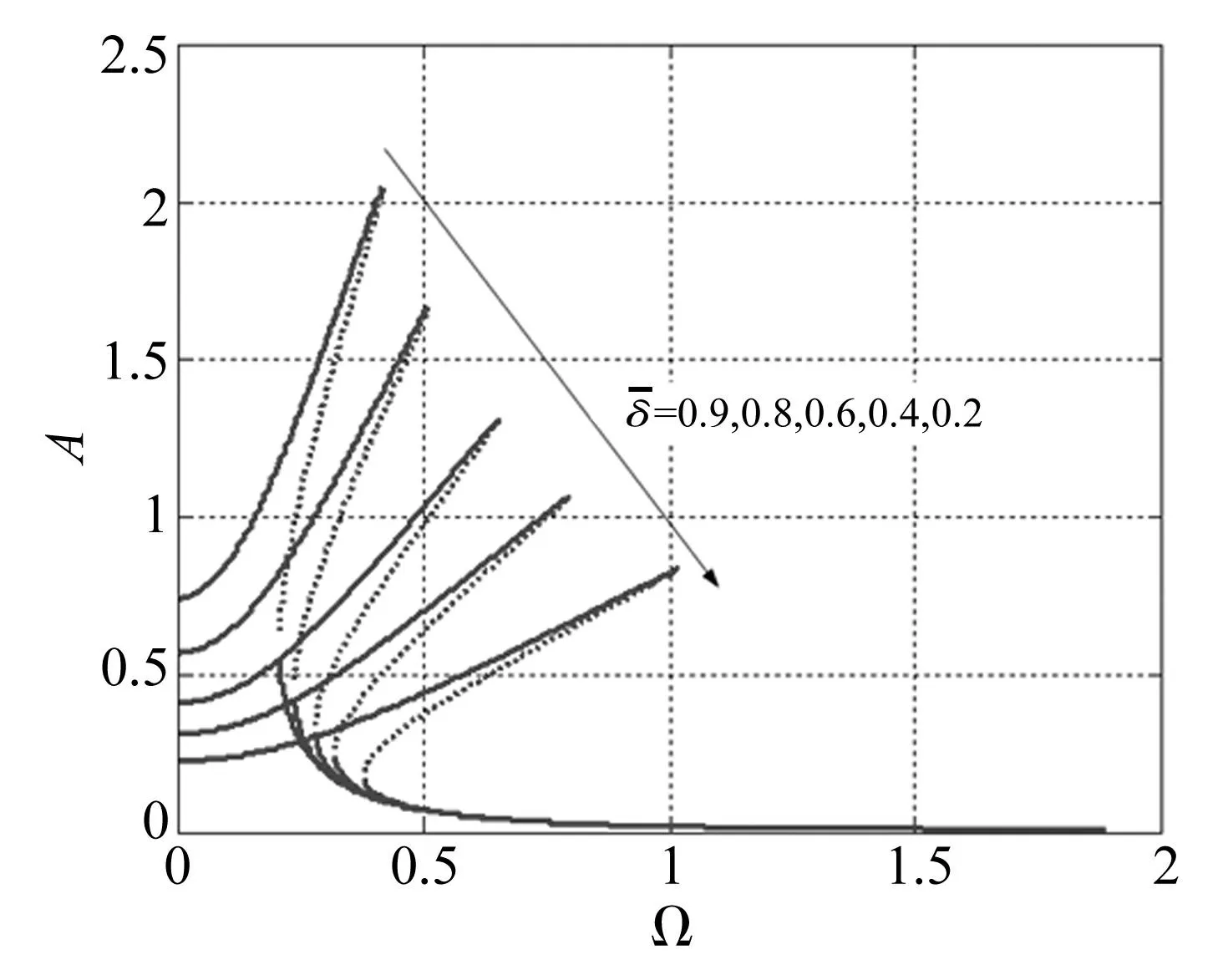
图3　幅频曲线(ζ=0.01，F 0=0.017) Fig.3 Amplitude-frequency Curve(ζ=0.01，F 0=0.017)

图4　传递率曲线(ζ=0.01，F 0=0.017) Fig.4 Transmissibility curve(ζ=0.01，F 0=0.017)

(2) 阻尼对力传递率影响较大(见图5)，当ζ=0.08时，系统已不存在多解，共振支完全得到抑制。但增大阻尼会严重影响高频隔振效果。

图5　阻尼对传递率的影响 (δ=0.9，F 0=0.017) Fig.5 Damping effect on the transfer rate(δ=0.9，F 0=0.017)

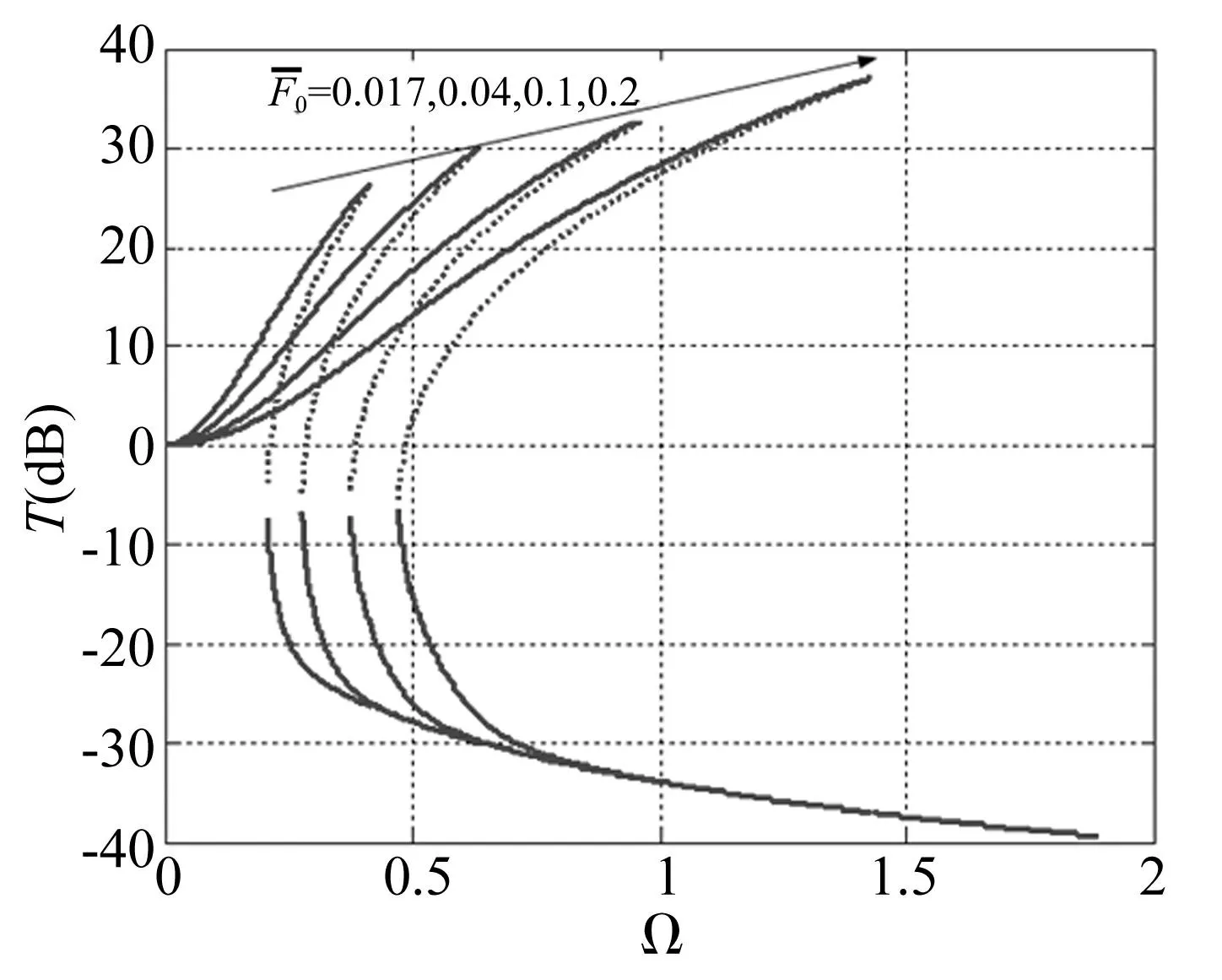
图6　激励幅值对传递率的影响 (δ=0.9，ζ=0.01) Fig.6 Excitation amplitude effect on the transfer rate (δ=0.9，ζ=0.01)

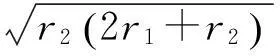
4ADAMS仿真计算

4.1仿真模型

将图1准零刚度隔振器经过适当数学简化，水平和竖直橡胶简化为螺旋弹簧，滚珠简化成滚柱，建立起ADAMS仿真模型(见图8)。

根据被隔振设备的重量及隔振器的布置位置与数量，可知每个隔振器需支撑W=360 kg的重量，此时要求竖向橡胶元器件的压缩量为δv=5 mm，所以：

kv=W/δv=7.056×105N/m

(18)

kh=kv/1.8=3.92×105N/m

(19)

设计r1=2.5 mm,r2=1.5 mm,则水平压缩量δ=0.9(r1+r2)=3.6 mm，从而水平预紧力:FH=khδ=1 411.2N

图8　隔振器ADAMS模型 Fig.8 Vibration isolator ADAMS model

4.2仿真结果

从1 Hz开始，每隔0.5 Hz进行一次仿真分析，采集支座反力的响应信号，并取响应的均方根作为传递力响应的幅值，其与激振力幅值的比值定义为力传递率，以此评价隔振系统的性能。力传递率曲线(见图9)，图9中实线表示准零刚度隔振器的传递率曲线，点画线为对应的线性隔振系统(即去掉水平橡胶弹簧，仅留下竖直弹簧的系统)的传递率。由图9可知，线性系统的起始隔振频率为17.8 Hz，而准零刚度系统的最低隔振频率仅为4.65 Hz。而且，在准零刚度隔振系统的有效隔振频率区间内，力传递率比线性系统小，尤其是在低频阶段，高频阶段二者隔振性能相当。因此，准零刚度隔振系统具有线性系统无法比拟的低频隔振性能。

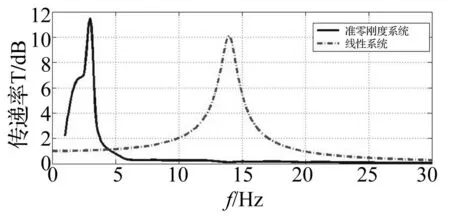
图9　隔振器传递率 Fig.9 Transmissibility of isolator

5隔振器试验

将加工制作好的滚球型准零刚度隔振器在静态实验台上连续加载、卸载，得出实验曲线(见图10)，图10(b)为水平弹簧不压缩、仅有竖直弹簧单独加载和卸载时的曲线，从图10(b)中可知，除去开始加载部分的误差，曲线基本表现为线性曲线，符合普通圆柱螺旋弹簧的力学特性，并可计算出弹簧刚度为k′=193 N/m；图10(c)中，是竖直弹簧和两水平弹簧都参与系统加载和卸载，在变形为0～2.5 mm过程中，基本表现为线性弹簧的力学特性，当加载到4～7 mm区域时，隔振器随着加载台的下移，变形量增加，所受的力却基本保持不变，出现了前述的“准零刚度”特性，这从试验角度上验证了静力学理论分析的正确性。

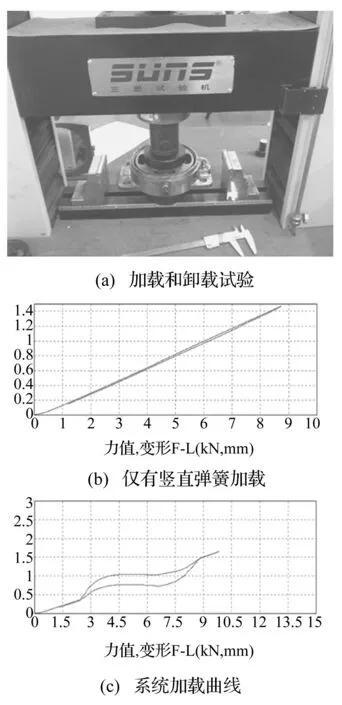
图10　隔振器静态试验 Fig.10 Static trial of isolator

同时，使用HEV-200激振器对实际滚球型准零刚度隔振器进行了隔振性能动态试验，如图11(a)和图11(b)所示。在水平振动台(即承载重物的部件，图1(a)中“4”)和隔振器底座(图1(a)中“12”)上都安装了力传感器，以测量这两个部位的力学动态响应。试验中实际隔振器承载的重物质量为m′=100 Kg，根据静态实验中测出的竖直弹簧刚度，可计算出线性系统固有频率：

(20)

从而起始隔振频率为：

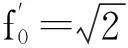
(21)

图11　隔振器动态试验 Fig.11 Dynamic trial of isolator

试验准备好后，输入正弦激励信号，当配重块随着激振器振动起来以后，采集水平振动台和底座两部位力传感器数据，以横坐标表示频率、纵坐标表示传递率(底座力值除以振动台力值)，绘制成曲线(见图11(c))。图11(c)中频率为5 Hz时，传递率为2.85，表明实际隔振器自振频率为5 Hz；频率为6 Hz时，传递率为0.986 7，表明实际隔振器的起始隔振频率由前述线性系统的10 Hz降低到6 Hz左右。实际隔振器试验证明：与相应的线性隔振系统相比，滚球型准零刚度隔振器的滚球装置提供的负刚度，通过与竖直弹簧并联，使准零刚度系统的自振频率和起始隔振频率均降低。因此，本设计的准零刚度隔振器具备低频隔振性能。

6结论

针对微幅振动下的低频隔振，设计了一款带滚球装置的准零刚度隔振器，并对其静、动力学特性进行了理论分析、数值仿真及试验分析。研究表明，激励幅值、阻尼对系统隔振性能影响显著，激励幅值越小、阻尼较大，隔振低频隔振性能越好。数值仿真结果揭示，准零刚度隔振系统起始隔振频率远低于相应的线性系统，且在低频范围内，力传递率远小于线性系统。因此，本设计的滚球型准零刚度隔振器具有高静态、低动态刚度等优良特性，可以有效降低系统的自振频率，能在低频段内有效隔振又能承受较大载荷。

参 考 文 献

[1] 朱石坚，楼京俊，何其伟，等. 振动理论与隔振技术[M]. 北京：国防工业出版社，2006.

[2] 肖斌. 柴油机双层隔振台架主动隔振技术研究[D]. 哈尔滨：哈尔滨工程大学，2008.

[3] 陈斌. 浮筏隔振系统建模及振动主动控制研究[D]. 合肥：中国科学技术大学，2008.

[4] 王刚.声子晶体局域共振带隙机理及减振特性研究[D].长沙: 国防科技大学, 2005.

[5] Alabuzhev P, Gritchin A, Kim L, et al. Vibration protecting and measuring system with quasi-zero stiffness[M]. New York: Taylor & Francis Group, 1989.

[6] 赵智. 气动可调式准零刚度隔振器的特性分析及实验研究[D]. 长沙：湖南大学，2013.

[7] 关肇直，陈文德. 谐波平衡法的理论基础[J]. 科学通报，1981, 29(20): 1217-1220.

GUAN Zhao-zhi,CHEN Wen-de. The theoretical basis of harmonic balance method[J]. Science Bulletin,1981,29(20): 1217-1220.

[8] Brennan M J, Kovacic I, Carrella A, et al. On the jump-up and jump-down frequencies of the Duffing 225 oscillator[J]. Journal of Sound and Vibration, 2008, 318(4): 1250-1261.

[9] Carrella A,Brennan M J,Waters T P. Force transmissibility of a nonlinear vibration isolator with high-static-low-dynamic-stiffness[C].Sixth EUROMECH Nonlinear Dynamics Conference,June 30-July 4,2008,Saint Petersburg,RUSSIA.

[10] Carrella A,Brennan M J,Kovacic I,et al. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J].Journal of Sound and Vibration,2009(332):307-317.

[11] 路纯红，白鸿柏. 新型超低频非线性被动隔振系统的设计[J]. 振动与冲击,2011,30(1):234-236.

LU Chun-hong,BAI Hong-bai.New design of ultra-low frequency nonlinear passive vibration isolation system [J].Journal of Vibration and Shock,2011,30(1):234-236.

[12] 彭献，黎大志，陈树年.准零刚度隔振器及其弹性特性设计[J].振动、测试与诊断,1997,17(4): 44-46.

PE Xian,LI Da-zhi,CHEN Shu-nian.Quasi-zero-stiffness design of vibration isolator and its elastic properties [J]. Journal of Vibration Measurement and Diagnosis,1997,17(4):44-46.

[13] 彭献，张施祥. 一种准零刚度隔振系统的静力与线性动力特性分析[J].湖南大学学报:自然科学版,2011,38(8): 34-39.

PE Xian,ZHANG Shi-xiang.A kind of quasi zero stiffness static and linear dynamic characteristics analysis of vibration isolation system [J]. Journal of Hunan University:Natural Sciences, 2011,38(8): 34-39.