基于希尔伯特黄变换的刀具磨损特征提取

第一作者 孙惠斌 男，博士，副教授，1977年生

通信作者 牛伟龙 男，硕士，1989年生

基于希尔伯特黄变换的刀具磨损特征提取

孙惠斌，牛伟龙，王俊阳

(西北工业大学 机电学院，西安710072)

摘要：概述了希尔伯特黄变换(HHT)的基本理论和算法，对信号经过经验模态分解(EMD)后得到的固有模态函数(IMF)求取振幅均值，差值筛选出与刀具磨损相关的IMF分量，并对单分量固有模态函数求取边际谱，获取边际谱最大幅值点，建立他们与刀具磨损之间的映射关系，进行特征提取，将其作为神经网络的输入特征向量，结合希尔伯特三维时频谱进行刀具磨损状态的判断。研究结果证明，该方法可以作为刀具磨损监测中信号特征提取的一种简单和可靠的方法。

关键词：希尔伯特黄变换；小波去噪；固有模态函数；希尔伯特谱；边际谱

基金项目：陕西省自然科学基金(2013JM7001);西北工业大学基础研究基金( JC20110215);西北工业大学研究生创业种子基金

收稿日期：2013-11-01修改稿收到日期：2014-03-03

中图分类号:TH165；TN911文献标志码： A

Tool wear feature extraction based on Hilbert-Huang transformation

SUNHui-bin,NIUWei-long，WANGJun-yang(School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:After presenting the basic theory and algorithm of Hilbert-Huang transformation (HHT), a tool signal was decomposed with the empirical mode decomposition (EMD) method and its intrinsic mode functions (IMFs) were gained to obtain their average amplitude. The IMF components related to tool wear were chosen using a difference screen. Meanwhile, the marginal spectrum of a single intrinsic mode function was obtained and its maximum amplitude point was then found. By establishing the mapping relationship between maximum amplitude points and tool wear, the features of tool wear were extracted. Regarding them as input eigen-vectors of a neural network, and combined with Hilbert spectra, the tool wear status judgment was implemented. The study results showed that this approach is a simple and reliable method to detect the level of tool wear.

Key words: Hilbert-Huang transformation; wavelet domain denoising; intrinsic mode function (IMF); Hilbert spectrum; marginal spectrum

刀具是加工过程中最常见也是最重要的加工要素之一，其磨损状态直接影响了加工工件的质量和精度。研究刀具磨损状态的监测具有重大的意义，不仅可以大大提高机械加工效率,而且可以降低加工成本，有着较大的经济效益。由于直接监测刀具磨损难度大，间接监测刀具磨损已成为一个重要研究方向。其主要技术路线是：

(1) 信号采集：通过力、加速度、声发射、功率等一些相应的传感器对刀具加工过程中的一些信号进行采集。

(2) 信号处理：通过一些现有的信号处理方法(如：傅里叶变换、小波变换[1]等)对采集的信号进行分析。

(3) 特征提取：信号处理完毕后将刀具正常磨损和严重磨损状态下信号处理结果进行对比，找出它们之间的不同，并与磨损状态建立相应的映射关系。

(4) 智能决策：根据提取的特征对刀具磨损状态进行识别和判断，如模式识别、专家系统、神经网络。

其中，信号处理是一个关键环节，它可以将刀具磨损从数据中进行定量描述，信号处理方法也决定了可提取到的磨损特征，以及智能决策的可靠性。但传统的傅里叶变换、短时傅里叶变换、小波变换等信号处理方法存在以下不足：

(1) 傅里叶变换只能处理线性非平稳的信号，小波变换虽然在理论上能处理非线性非平稳信号，但在实际算法实现中却只能处理线性非平稳信号。

(2) 不具有自适应性，傅里叶变换的基是三角函数，小波变换的基是满足“可容性条件”的小波基。①一旦选定了基函数，那么就必须用这种基函数来分析所有的数据；②选定了分解尺度，所得到的结果是某一固定频率段的时域波形，所包含的频率只与信号的分析频率有关，而与信号本身无关。不能准确的反映被分析信号的特性。

(3) 受Heisenberg测不准原理制约，即时间窗口与频率窗口的乘积为一个常数。这就意味着如果要提

高时间精度就得牺牲频率精度，反之亦然，不能在时间和频率同时达到很高的精度。

(4) 需要预先选择基函数，其计算方式是通过与基函数的卷积产生的,这就导致了傅里叶变换的频率是全局性的，小波变换是区域性的，不能对信号局部特征进行精确的分析。

希尔伯特黄变换则不同于这些传统方法，它彻底摆脱了线性和平稳性束缚[2]，其适用于分析非线性非平稳信号，能够自适应产生“基”，即由“筛选”过程产生的IMF为它的基函数。同时也不受Heisenberg测不准原理制约，可以在时间和频率同时达到很高的精度，并借助Hilbert变换求得相位函数，再对相位函数求导产生瞬时频率,这样求出的瞬时频率是局部性的，对局部特征反映更为准确。因此，希尔伯特黄变换从很大程度上弥补了传统信号分析方法的不足，使得它比传统信号的时频分析更优越，因而具有更好的应用前景和更广的应用空间[3-4]。这里就希尔伯特黄变换对刀具磨损监测过程中振动信号的特征提取进行了分析和实例研究。

1希尔伯特黄变换

1.1EMD方法基本原理

Huang等[5]首次提出希尔伯特黄变换(Hilbert-Huang Transform HHT)，是一种全新的信号时频分析理论，在这一理论中，引入了固有模态函数(Intrinsic Mode Function, IMF)[6]的概念,在经验模态分解(Empirical Mode Decomposition, EMD)的基础上[7]，对每个IMF进行Hilbert变换得到瞬时频率[8]，从而将信号精确表示成频率-时间-能量(或者幅度)的分布，称为Hilbert谱。HHT的特点在于它是基于信号局部特征，能够自适应的高效分解,而且它特别适用于分析非线性非平稳信号。

EMD是HHT的一个关键步骤,首先找到信号x(t)x(t)的极大值和极小值,通过三次样条拟合,从而得到信号的上包络线U(t)和下包络线L(t),计算上、下包络线的均值m1，然后再计算x(t)-m1=h1。

判断h1是否为一个IMF的标准是：

(1) 在整个数据段内，极值点的个数和过零点的个数必须相等或最多相差一个；

(2) 在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零，也就是说，上下包络线相对于时间轴局部对称。理想情况下，如果h1是一个IMF，那么h1就是x(t)的第1个IMF分量；如果h1不满足IMF的条件，把h1作为原始数据，重复上述分解过程，得到上下包络线的平均值m11，再判断h11=h1-m11是否满足IMF的条件，如不满足，则重复循环k次，得到h1(k-1)-m1k=h1k使得h1k满足IMF的条件。记c1=h1k，则c1为信号x(t)的第1个满足IMF条件的分量。

将c1从x(t)中分离出来，得到：

r1=x(t)-c1

(1)

将r1作为原始数据，重复上述步骤，依次筛选出n个满足IMF定义的分量(r1,r2,…,rn)，当rn为一个单调函数或只有一个极值时停止循环，于是信号可以被写成：

(2)

式中:rn为残余函数，代表信号的平均趋势。

1.2Hilbert变换

对EMD 分解得到的每个IMF 分量应用Hilbert 变换，Hilbert变换相当于将一个信号x(t)与1/πt做卷积：

(3)

式中:P为柯西主分量，得到的解析信号为：

Z(t)=X(t)+iY(t)=a(t)eiθ(t)

(4)

其中

(5)

(6)

则瞬时频率[9]ω(t)定义为：

(7)

由于EMD分解得到的IMF均为单分量信号，故对其进行Hilbert变换可得到信号的瞬时频率，瞬时相位和瞬时幅值。

1.3希尔伯特谱和边际谱

把式(2)～式(6)所表示的变换用于每个固有模态函数序列，数据便可表示为下式：

(8)

(9)

(10)

把三维时频谱经过对时间的积分，便形成了只有频率和幅值的二维谱图。这种由HHT得到的边际谱与Fourier频谱有相似之处。从统计观点上来看，HHT边际谱表示了该频率上振幅(能量)在时间上的累加，能够反映各频率上的能量分布，但因为瞬时频率定义为时间的函数，不同以往Fourier等需要完整的振荡波周期来定义局部的频率值，而且求取的能量值不是全局定义的，因此HHT边际谱对信号的局部特征反映更为准确。尤其是在分析非平稳信号时，这种定义对于频率随时间随时变化的信号特征来说，能够最真实地反映振动特点。而Fourier频谱的某一点频率上的幅值则表示的是在整个信号里有一个含有此频率的三角函数组分。因此，边际谱和傅氏谱的意义是不同的。

在刀具切削加工中，刀具的磨损是一个比较复杂的过程，而对刀具磨损的状态监测往往需要将刀具在正常磨损状态和严重磨损状态进行一定意义上的区分，即对信号进行特征提取，提取到的特征则要反映刀具磨损的状态。而选用希尔伯特黄变换，它能处理非线性非平稳信号[11]并具有较强的自适应性，而对于它经过EMD分解后所得每个本征模函数分量IMF都有相应的物理意义与其对应，这更方便于有针对性的对其进行研究与分析。除此之外，希尔伯特谱与希尔伯特边际谱也都可以在一定程度上反映出刀具磨损状态的特征。

2刀具磨损的特征提取方法

2.1IMF的振幅均值法

在实际应用领域中得到的信号总是混杂着一定的噪声，而噪声的存在严重干扰了信号的本来面目，不利于进一步的信号分析和处理。因此，在信号处理过程中对噪声加以消除或减少，以便最大程度地提取出有用的信号。为了增加研究分析的精确性和可靠性，先对采集的振动信号进行小波阈值去噪[12-13]，再对其进行希尔伯特分析。

经过小波去噪和EMD分解后，任何复杂的信号都可分解为为数不多的IMF且相互独立，每个IMF分量也都有相应的物理意义与其对应。因此，可以对IMF分量求振幅均值，除去那些与刀具磨损不相关的IMF分量，将加工过程中刀具与工件接触时所对应的IMF分量提取出，与刀具磨损状态建立相应的映射关系，作为刀具磨损的特征，由于离散采样，则振幅均值为：

(11)

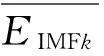
选择与磨损相关的IMF分量时，可以利用差值方法来进行筛选，在三种不同磨损状态下，加工参数中只有刀具磨损量改变较大，其它的加工参数基本不变，因此只有刀具与工件接触时所对应的IMF分量会随着刀具磨损的加剧而产生明显的变化，即三种状态下它们的振幅均值的差值比较大。实验表明，当它们的振幅差值大于1.5时，都可以认为它们是与刀具磨损相关的IMF分量的振幅均值：

(12)

(13)

式中:IMFki、IMFkm、IMFkn分别表示的是严重磨损、正常磨损、初期磨损下的IMF分量的振幅均值。

边际谱可以比较准确的反应信号的实际频率，由于在加工过程中受到环境等因素的干扰，经过EMD分解后的IMF分量中有些反映的是与刀具加工过程无关的信号。因此，只要选出能反映加工时刀具切削工件所对应的IMF，该IMF包含的能量和信息是最多的，单独对其求边际谱即可，设第k个IMF分量满足条件，即反应刀具切削工件时所包含最多的能量和信息，用于式(2)～式(6)所表示的变换，则它的边际谱：

I(t)=ak(t)ejθk(t) =ak(t)ej∫ωk(t)dt

(14)

H(ω,t)=ak(t)ej∫ωk(t)dt

(15)

(16)

对于它的边际谱，由于磨损状态的不同，它们的最大幅值点相差明显，故可以将其最大幅值点作为磨损特征进行提取。

希尔伯特三维时频幅值谱，表示在不同频率和时间点下的能量振幅，可以根据它在不同磨损状态下表现出来的频率幅值的变化以及波动幅度大小作为判断刀具磨损状态的辅助参考。

刀具磨损监测过程其实也是一个智能决策[14]的过程，而人工神经网络是智能决策中一种十分有效的方法。通过神经网络建立信号特征和刀具磨损状态之间的对应关系来识别刀具的磨损状态,是目前刀具磨损识别研究者广泛采用的一种方法，对刀具磨损特征提取完毕后，可以将上述特征作为神经网络的输入特征向量，对神经网络进行训练和识别。

图1为基于希尔伯特黄变换的刀具磨损监测系统流程，图1中IMFk1、IMFk2、IMFk3为加工过程中刀具与工件接触时所对应的IMF分量的振幅均值，IMFks为包含能量和信息最多的固有模态函数，求其边际谱最大幅值点，将他们作为神经网络的输入特征向量，进行神经网络的训练和状态识别，随后反馈给计算机，计算机再根据反馈结果对机床进行自动换刀。

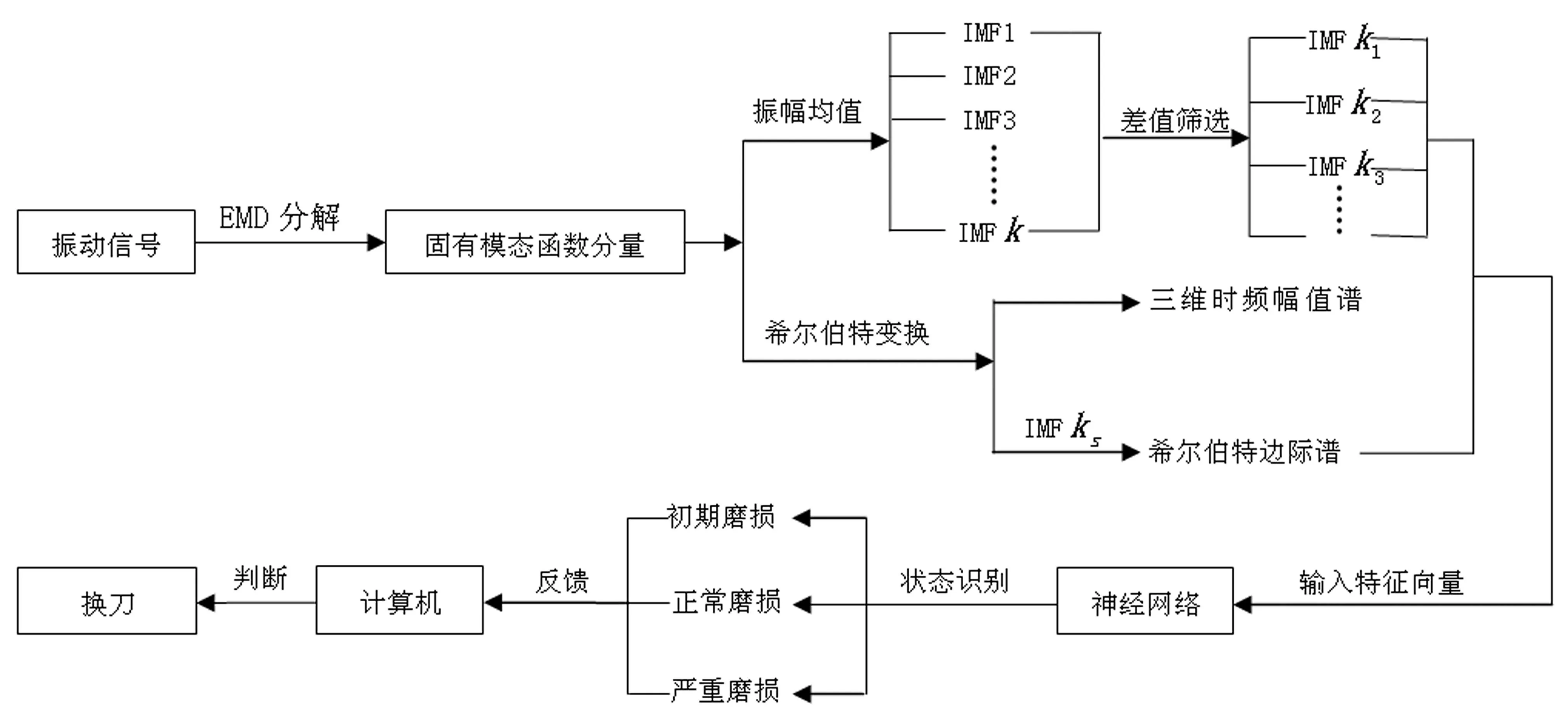
图1　基于希尔伯特黄变换的刀具磨损监测系统 Fig.1 Tool wear monitoring system based on Hilbert Huang Transform

3实验结果与分析

本实验采用C000031-CNC4240小型数控铣床，材料采用45#调制钢，硬度：HB200，尺寸：70 mm×50 mm× 50mm，刀具采用苏州AHNO生产的型号为Eco-U13φ×25 mm×75 mm的4刃整体HM平头硬质合金立铣刀。传感器采用KISTLER公司生产的型号为8702B100M1单轴加速度计(±100 g，与地绝缘，灵敏度50 mV/g)，对Z轴方向进行振动信号采集。除此，本实验还采用了便携式数据采集系统主机，DEWSOFT公司生产的DEWSOFT-43，并设置采样频率为20 kHz，实验平台(见图2)。

图2　实验平台 Fig.2 Experiment platform

在铣削过程中，刀齿从极薄的切削层下切入工件，有挤压的滑行并伴随着高温高压，铣刀的前刀面和后刀面经常与工件表面发生强烈的摩擦，因此生产中以后刀面磨损宽度VB作为判断铣刀磨损程度的一个标准(见图3 )，实验规定刀具初期磨损量VB为0～0.05 mm，正常磨损量VB为0.05～0.3 mm，当大于0.3 mm时为严重磨损。

图3　刀具磨损的测量 Fig.3 Measurement of tool wear

为了全面和准确分析，找出最佳水平组合，使得指标最优，且要减少试验次数和试验复杂程度。实验采用正交试验方法[15]，根据切削三要素和刀具磨损量指定如下方案(见表1)：

在1∶5万航磁ΔT异常等值线平面图和剖面平面图上，异常呈近EW向带状展布，长度约40km，上桃园以西，ΔT>400nT的区域NW向长度约18km，NS向宽度约2.5km，异常特征为南部磁场变化缓慢、梯度小且无明显的局部负异常，而其北部磁场变化较快、梯度较大且有较强的局部负异常相伴生；上桃园向东，磁场呈现出剧烈跳跃变化的特征，在向城镇南侧由于铁矿体埋深较大，磁场变化也变得较平稳；而其南支场值变化较复杂，异常形态为不规则状。经对异常向上延拓处理。异常极大值的轴向几乎没有改变，只是其水平位置略向南移动，由此可知引起磁异常的异常源应为向下延深较大，略向南倾的磁性体。

表1　因素水平表(三因素四水平)

以表1为依据，分别对刀具初期磨损、正常磨损和严重磨损状态下的振动信号进行采集，共采集48组信号，图4为主轴转速V=800 r/min，进给速度f=12.5 mm/min，切削深度ap=1 mm下严重磨损状态下的原始信号和经过小波去噪后的信号：

图4　原始信号与去噪后的信号 Fig.4 Original signal and denoised signal

图5是刀具在严重磨损状态下的EMD分解，其切削参数为：主轴转速V=800 r/min，进给速度f=12.5 mm/min，切削深度ap=1 mm。图6为原始信号的重构，因为 EMD分解在原理上是完备的，也就是说它每次都在原始信号中减去一个分量，最后剩余一个趋势分量，因此将各个IMF以及余量求和便可得到完全一样的原始信号。除此之外，可以在重构过程中发现，信号的几个高频分量叠加即可反映原始信号的一系列特征，而不用将信号所有IMF 进行叠加，即只要将在原始信号中确实存在的高频分量成分叠加即可。从图6中就可以看出，当叠加到高频分量IMF9时，信号基本上就与原始信号相同了。

图5　信号的EMD分解 Fig.5 Signal’s EMD

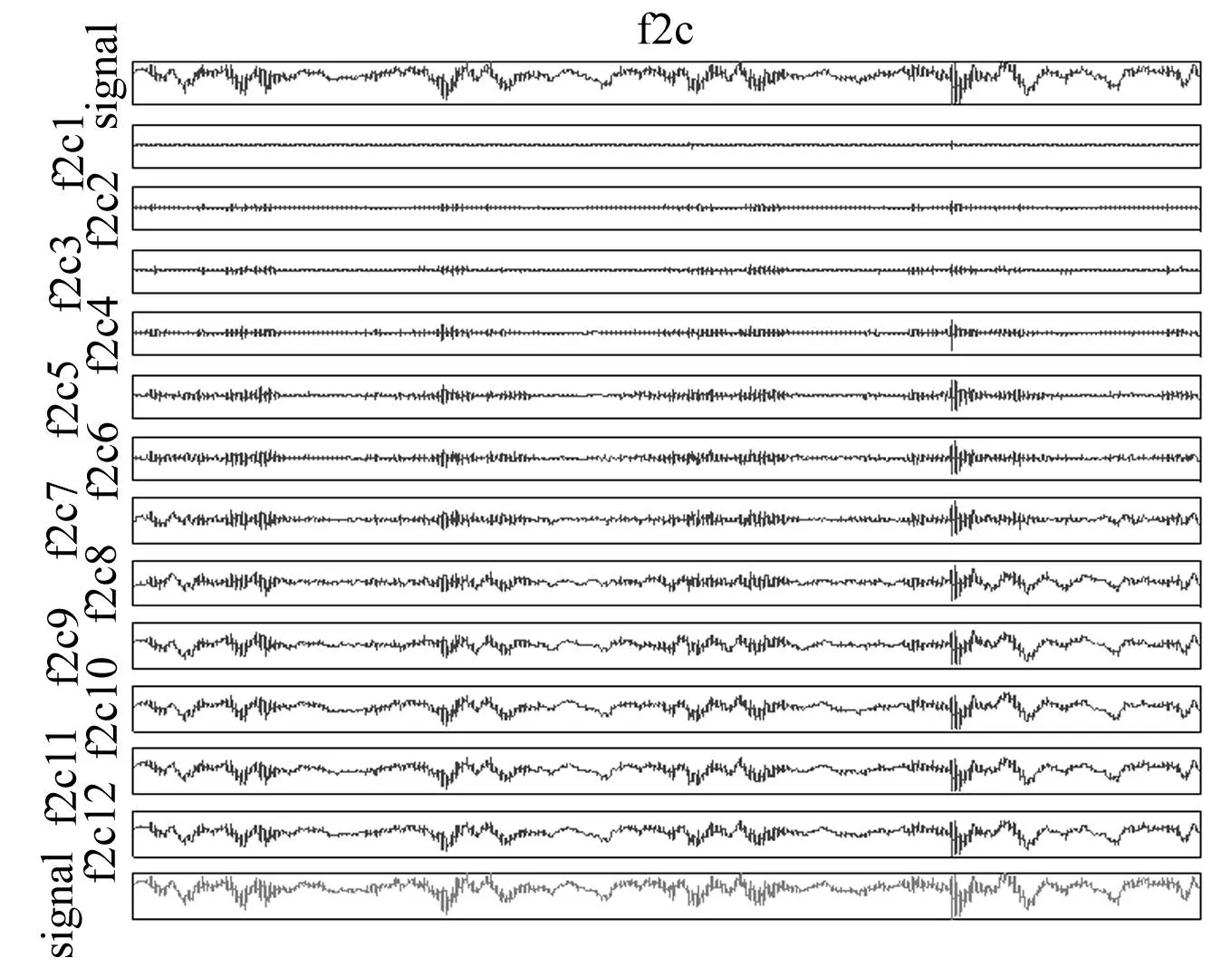
图6　信号的重构 Fig.6 Signal reconstruction

图7　IMF平均振幅 Fig.7 IMF average amplitude

如图7为不同磨损状态下的各个IMF分量的振幅均值。可以发现初期磨损、正常磨损与严重磨损状态下的IMF1、IMF2、IMF7、IMF8、IMF9、IMF10 、IMF11、IMF12振幅差值都不是很大，而IMF3、IMF4、IMF5、IMF6则有明显的差值，且大于1.5，因此IMF3、IMF4、IMF5、IMF6为刀具与工件接触时所对应的IMF分量，同时随着刀具磨损的增大,刀具切削工件时对应的IMF分量的振幅均值也在明显的增大。因此，可以将IMF3、IMF4、IMF5、IMF6振幅均值作为刀具磨损的特征进行记录和提取。尽管这些结果不是线性的，但足够训练任何的神经网络。

经过EMD分解后，对每个IMF分量进行希尔伯特变换，可以得到希尔伯特三维时频幅值谱，为了便于观察和分析，从不同状态下的信号中随机截取1 200个采样点并放大信号，如图8、图9和图10，其切削参数为：主轴转速V=400 r/min，进给速度f=10 mm/min，切削深度ap=0.6 mm，比较三种磨损状态，可以发现在初期磨损和正常磨损状态下幅值在不同频率下变化不是很明显，曲线波动变化不是很大，而严重磨损则正好相反，并且在图中低频处出现明显的散乱点，这都可以作为刀具磨损特征提取的参考。

图8 初期磨损状态下三维时频幅值谱Fig.8Hilbertspectrumforinitialworn图9 正常磨损状态下三维时频幅值谱Fig.9Hilbertspectrumfornormalworn图10 严重磨损状态下三维时频幅值谱Fig.10Hilbertspectrumforseverelyworn

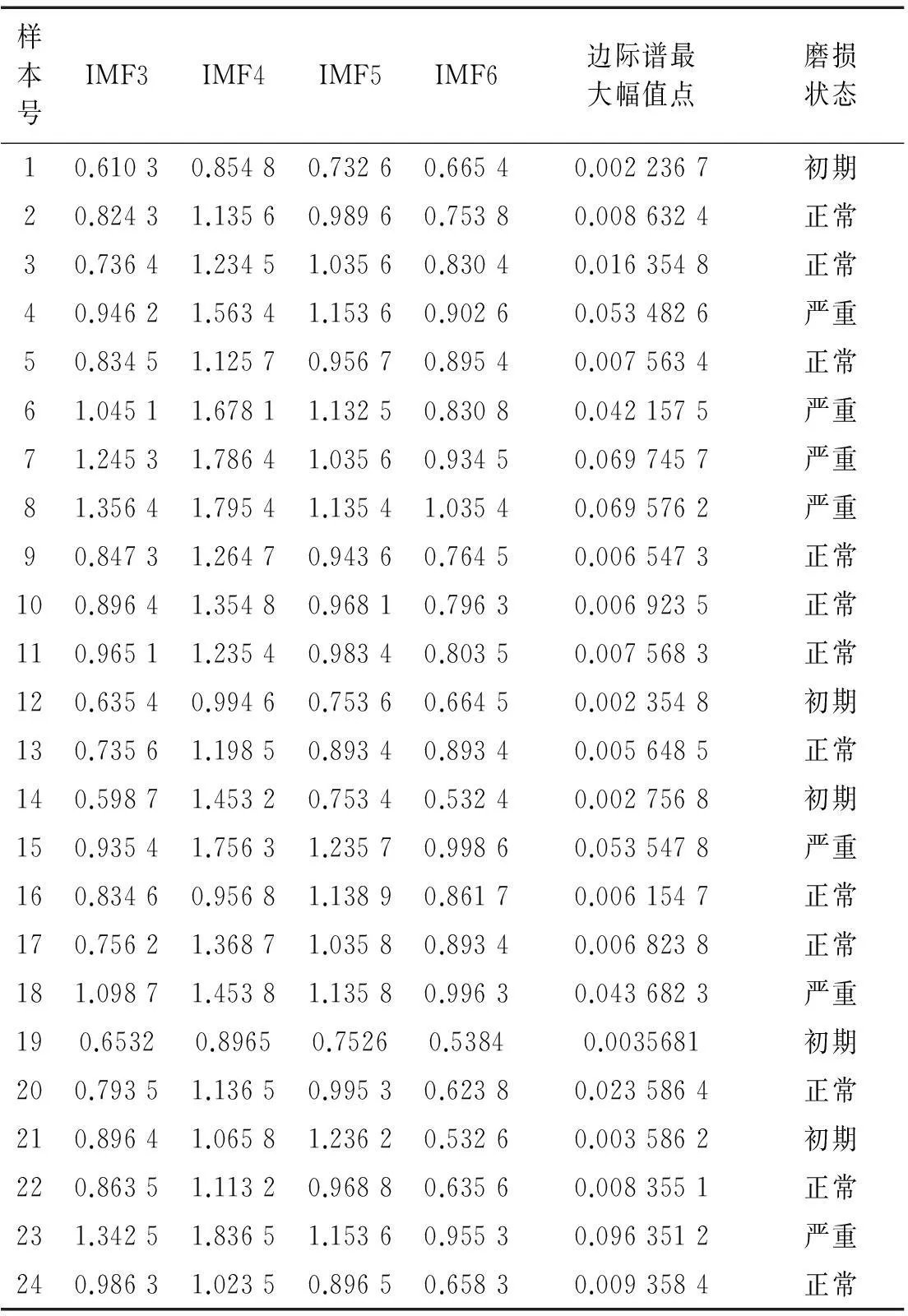
表2　磨损特征

图11、图12和图13分别为刀具初期磨损、正常磨损和严重磨损状态下的IMF4分量的希尔伯特边际谱，其切削参数为：主轴转速V=800 r/min，进给速度f=12.5 mm/min，切削深度ap=1 mm，从图中可以看出初期磨损和正常磨损状态下它的边际谱最大幅值点为0.002 764 2、0.007 451 3，而严重磨损状态下边际谱最大幅值点为0.042 157，即随着刀具磨损的加剧，它的边际谱最大幅值点也在随着增大，且增幅明显。

经过试验得到的不同切削状态和不同磨损状态下的48组数据，从中随机选取16组数据作为神经网络的训练样本，随机选取8组数据作为神经网络的目标样本，经过希尔伯特黄变换处理提取特征，如表2，将前16组作为训练样本，后8组作为目标样本：

将上述IMF和边际谱最大幅值作为神经网络的输入特征向量输入神经网络，由于BP神经网络每次训练都有随机数的产生，故将输入特征向量进行5次训练和5次神经网络判断，取平均值，结果(见表3)：

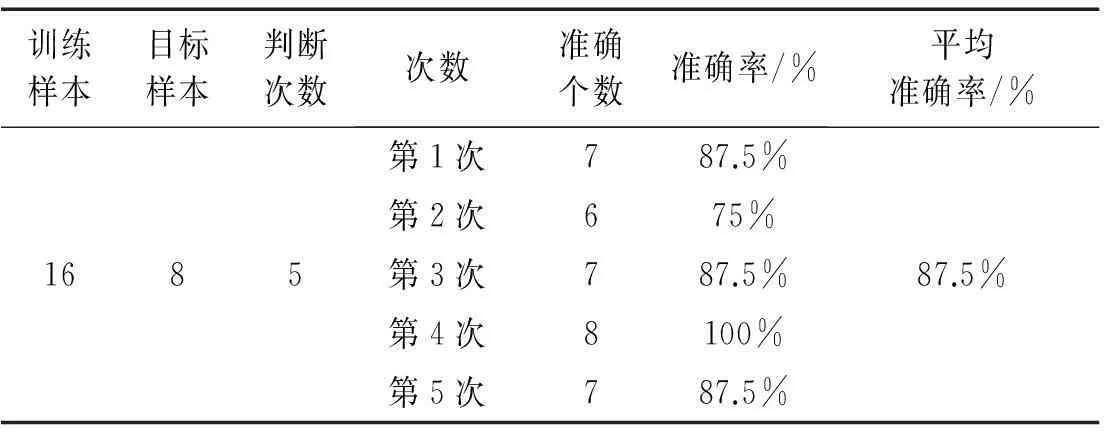
表3　实验结果

图11 初期磨损状态下IMF4希尔伯特边际谱Fig.11MarginalspectrumofIMF4forinitialworn图12 正常磨损状态下IMF4希尔伯特边际谱Fig.12MarginalspectrumofIMF4fornormalworn图13 严重磨损状态下IMF4希尔伯特边际谱Fig.13MarginalspectrumofIMF4forseverelyworn

4结论

针对目前刀具磨损监测中信号特征提取方法的不足，提出了一种在小波去噪的基础上运用希尔伯特黄变换来进行刀具磨损特征提取的方法，得出以下结论：

(1) 该方法可以将不同频率下的信号逐步分离，方便找出与刀具磨损相关的敏感信号，有助于有目的性的分析。

(2) 弥补了传统信号分析方法的高分辨率和自适应不足，有效的反映和保留了刀具磨损时的非线性非平稳信号的特征。

(3) 所提取的刀具磨损特征IMF3、IMF4、IMF5、IMF6的振幅均值和边际谱中的最大幅值能准确可靠地反应刀具磨损状态。

结果证明，基于希尔伯特黄变换的刀具磨损特征提取可以作为刀具磨损监测的一种简单和可靠地方法。但由于加工条件的复杂性和加工过程中的不稳定性，周围环境的干扰噪声严重的影响了信号的分析精度，因此也需要通过合理的方式消除或减少噪声的干扰，仅靠小波去噪的方式是远不够的，除此之外，目前的智能决策方法如神经网络、支持向量机等都有它本身的局限性和对样本的依赖性，对于造价昂贵且特质的刀具，建立刀具磨损样本数据库是不现实的，因此，进一步在HHT的基础上研究基于小样本的刀具磨损智能决策方法也是研究的一大重点。

参 考 文 献

[1] Zhu K P,Wong Y S, Hong G S. Wavelet analysis of sensor signals for tool condition monitoring:A review and some new results [J]. International Journal of Machine Tools & Manufacture 2009,49:537-553.

[2] 吴琛,周瑞忠. 基于 Hilbert 谱的结构动力响应非线性特征分析[J]. 振动与冲击,2013, 32(14):71-76.

WU Chen ，ZHOU Rui-zhong. Nonlinear behavior analysis of structural dynamic response based on Hilbert spectrum[J]. Journal of Vibration and Shock,2013,32(14):71-76.

[3] 陈双喜，林建辉，陈建政. 基于希尔伯特-黄变换提取车辆轨道耦合系统时频特性[J].振动与冲击,2013,32(5):43-47.

CHEN Shuang-xi,LIN Jian-hui, CHEN Jian-zheng.Time-frequency characteristics extraction of vehicle-track coupling system based on Hilbert-Huang transform[J]. Journal of Vibration and Shock, 2013,32(5):43-47.

[4] Raja J E,Kiong L C,Soong L W. Hilbert-Huang transform-based emitted sound signal analysis for tool flank wear monitoring[J]. Arabian Journal for Science and Engineering，2013，38:2219-2226,

[5] Huang N E，Shen Zheng，Long S R，et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]．Proc. R. Soc. Lond. 1998，A：903-995．

[6] Bisu C F, Zapciu M,Cahuc O,et al. Envelope dynamic analysis: a new approach for milling process monitoring[J]. The International Journal of Advanced Manufacturing Technology,2012,62(9),471-486,

[7] Du Wei, Liu Quan. A new ball bearing fault diagnosis method based on EMD and SVM[J]. Advanced Electrical and Electronics Engineering,2011, 2: 423-428.

[8] Gupta R,Kumar A,Bahl R. Estimation of instantaneous frequencies using iterative empirical mode decomposition[J]. Signal, Image and Video Processing,2012, 10(5):1863-1703.

[9] 符娆，张群岩，赵述元. 航空发动机试飞中转静子碰摩故障信号处理的希尔伯特-黄变换(HHT)方法[J].噪声与振动控制,2012,2:123-127.

FU Rao, ZHANG Qun-yan,ZHAO Shu-yuan. Signal processing of rubbing trouble between rotor and stator of aeroengines in flight-test using Hilbert-Huang transform [J]. Noise and Vibration Control, 2012,2:123-127.

[10] 钟佑明,秦树人,汤宝平. 希尔伯特-黄变换中边际谱的研究[J].系统工程与电子技术,2004,26(9):1324-1326.

ZHONG You-ming, QIN Shu-ren, TANG Bao-ping. Study on the marginal spectrum in Hilbert-Huang transform[J]. Systems Engineering and Electronics,2004.26(9):1324-1326.

[11] Bassiuny A M,Li X. Flute breakage detection during end milling using Hilbert-Huang transformand smoothed nonlinear energy operator[J].International Journal of Machine Tools and Manufacture 2007,47:1011-1020.

[12] 代海波，单锐，王换鹏，等. 基于改进阈值函数的小波去噪算法研究[J]. 噪声与振动控制,2012,44(6):189-193.

DAI Hai-bo,SHAN Rui,WANG Huan-peng,et al. Study on wavelet denoising algorithm based on iimproved threshold function and maximal overlap discrete wavelet packet transform [J]. Noise and Vibration Control, 2012,44(6):189-193.

[13] 唐进元，陈维涛，陈思雨，等. 一种新的小波阈值函数及其在振动信号去噪分析中的应用[J]. 振动与冲击，2009,28(7)：118-121.

TANG Jin-yuan, CHEN Wei-tao, CHEN Si-yu, et al.Wavelet-based vibration signal denoising with a new adaptive thresholding function[J]. Journal of Vibration and Shock, 2009,28(7)：118-121.

[14] 何正嘉，陈进，王太勇，等.机械故障诊断理论与应用[M].北京：高等教育出版社，2010.

[15] 李志西，杜双奎. 试验优化设计与统计分析[M].北京：科学出版社，2010.