基于MATLAB的矿石破碎机关键机构的运动学和动力学分析

基于MATLAB的矿石破碎机关键机构的运动学和动力学分析

王国成，段胜秋，杨昌明，胡文强

(西华大学机械工程学院，四川成都610039)

摘要：为精确获得矿石破碎机关键机构的运动规律及受力状态，采用矩阵法构建了矿石破碎机关键机构的运动学和动力学数学模型，针对位置问题涉及非线性超越方程组的求解，编制了采用牛顿数值法求解该问题的通用MATLAB程序，并利用MATLAB软件对该机构进行了运动学和动力学分析，实现分析结果的可视化，为机构的进一步深入研究提供了基础。

关键词:矿石破碎机运动学分析动力学分析牛顿数值法

中图分类号：TH113文献标识码：A

作者简介：王国成(1989-)，男，硕士研究生，主要研究方向：现代机械设计方法。

收稿日期：2015-04-21

Kinematic and dynamic analysis for the key mechanism of ore crusher based on MATLAB

WANG Guocheng，DUAN Shengqiu，YANG Changming，HU Wenqiang

Abstract:In order to accurately obtain the motion law and strained condition of the key mechanism of ore crusher, the mathematical models of kinematic and dynamic are set by matrix method.This paper establishes the general MATLAB program using Newton numerical method to solve nonlinear equation group, then kinematic and dynamic analysis of the key mechanism of the ore crusher is carried out using the software MATLAB. The results are made visual. This paper provides reference for further research.

Keywords:ore crusher；kinematic analysis；dynamic analysis；Newton numerical method

0引言

破碎机在矿物质开采过程中扮演着重要的角色，目前，对于破碎机的研究主要集中于运动特性的研究，获得了各个机构的运动规律以及关键点的运动轨迹，判断了机构之间是否发生干涉。但是破碎机工作环境通常比较恶劣，受力情况变化较大，仅仅进行运动学分析不足以设计出破碎机零件结构[1]。本文基于MATLAB仿真平台采用解析法对破碎机的运动学和动力学均进行了研究，不仅得到了各个构件的运动规律，同时获得了各个运动副的约束反力以及驱动力矩，为破碎机的动力学参数优化和结构设计提供载荷依据。

1运动学分析

图1　破碎机关键机构简图

机构的运动分析，主要获得机构中某些构件的位移、速度和加速度及某些点的轨迹、速度和加速度。破碎机关键机构运动分析求得各构件在各个位置的位移、速度和加速度，所得结果为后续动态静力分析计算惯性力及惯性力矩提供基础数据[2]。图1为某矿山破碎机关键机构的结构简图。

已知各构件尺寸为：

lAB=0.1m,lBC=0.46m,lCD=0.25m,lBE=0.46m,lEF=0.265m,lFG=0.67m,xD=0.3m,yD=0.5m,xG=0.43m，yG=0.21m

各构件质心尺寸为：

lBS2=0.3m，δ1=30°，δ2=15°，lDS3=0.11m，lES5=0.13m，lGS6=0.5m，构件1的质心在A点。

各构件质量分别为：

m1=2.0kg，m2=9.0kg，m3=4.5kg，m5=5.0kg，m6=15.0kg。

各构件绕其质心的转动惯量：J1=0.0015kgm2，J2=0.065kgm2，J3=0.017kgm2；J5=0.03kgm2，J6=0.5kgm2。

当曲柄转角处于90°≤θ1≤210°的范围内，矿石阻力为300N，集中作用于构件6的质心S6处，曲柄1以匀角速度ω1=20rad/s逆时针方向转动，对该机构进行运动学分析和动态静力分析。

1.1位置分析

解析法进行机构运动分析的关键是位置方程的建立和求解。速度分析和加速度分析是对位置方程作进一步的数学运算[3]。建立矿山破碎机关键机构的封闭矢量位移方程组[3-5]：

(1)

式中：θi为各杆矢量的方位角，rad，i=1,2,3,5,6。

1.2速度分析

将式(1)对时间t求一次导数，得速度矩阵方程：

(2)

式中：ω1为各杆件的角速度，rad/s，i=2,3,5,6。

1.3加速度分析

将式(1)对时间t求二次导数，得加速度矩阵方程：

(3)

式中：αi为各杆件的角加速度，rad/s2，i=2,3,5,6。

1.4MATLAB实现

位置问题方程组的求解涉及含三角函数的非线性超越方程组，其求解难度较大，而速度方程和加速度方程的求解，只需求解线性方程组，相对而言较容易。笔者针对此问题利用牛顿数值法求解非线性超越方程组[4]，使得求解过程大大简化，提高了求解的效率。应用MATLAB软件求解线性方程组的方法对速度矩阵和加速度矩阵进行求解，得到机构的运动规律。如图2所示。

图2　运动学仿真曲线

2动态静力分析

机构动力分析的任务是确定运动副的反力和需加于机构上的平衡力或平衡力矩[7]。动态静力分析需先求各构件的惯性力及惯性力矩。该矿山破碎机关键机构根据所确定的相关构件的加速度和角加速度，求得对应构件的惯性力(FI2x、FI2y、FI3x、FI3y、FI5x、FI5y、FI6x、FI6y)和惯性力矩(MI2、MI3、MI5、MI6)。其受力分析如图3所示。

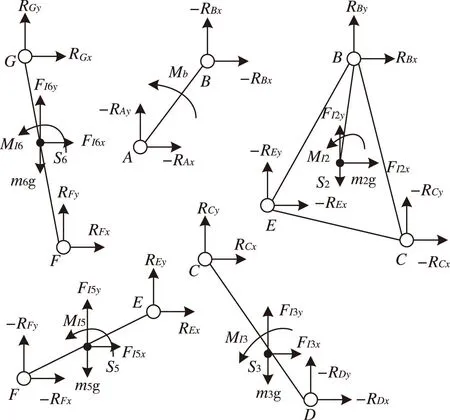
图3　破碎机关键机构受力分析

受力分析时，将各力分别沿x、y方向分解，然后就各构件分别列出力平衡方程式。

对于构件1平衡方程式为：

(4)

对于构件2平衡方程式为：

(5)

式中：

A=MI2+(yB-yS2)FI2x+(xS2-xB)(FI2y-m2g)

对于构件3平衡方程式为：

(6)

式中：

B=(yS3-yD)FI3x-(xS3-xD)(FI3y-m3g)-MI3

对于构件5平衡方程式为：

(7)

式中：

E=(yE-yS5)FI5x+(xS5-xE)(FI5y-m5g)+MI5

对于构件6平衡方程式为：

(8)

将构件平衡方程式整理成一个线性方程组，并写成矩阵形式。便于采用矩阵方程求解，用矩阵形式表示为：

CFR=D

(9)

其中

通过MATLAB编程，完成式(9)的求解，得到各运动副的反力和需加于曲柄上的平衡力矩。机构平衡力矩曲线、曲柄支反力曲线和运动副F反力曲线如图4所示。

图4　动力学仿真曲线

3结束语

本文运用MATLAB软件对矿山破碎机关键机构进行了运动学和动力学分析，得到了矿山破碎机关键机构的运动学和动力学特性。提出了针对位置问题求解非线性超越方程组的牛顿数值法程序，为相似构件的位置分析提供了参考。运动学和动力学分析结果为破碎机关键机构的强度校核提供了基本参数，为机构的进一步优化及深入研究提供了数据依据。该方法对于其它类型机构的运动学和动力学分析，具有普遍的适用性。

参考文献

[1]程发龙，杨春兰，黄大明.破碎机运动机构载荷特性分析与MATLAB求解[J].煤矿机械，2014,42(11)：74-79

[2]黄大明，杨春兰，蒋顺梅.基于MATLAB的破碎机动力学参数优化设计[J].机械设计与制造，2012(3)：28-30

[3]孙桓，陈作模，葛文杰.机械原理(第七版)[M].北京：高等教育出版社，2006

[4]郭仁生.机械工程设计分析和MATLAB应用[M].北京：机械工业出版社，2006

[5]郭飞，杨杰.插床机构运动规律在Matlab中的实现[J].华北水利水电学院学报，2010,31(4)：89-91

[6]王先安，皮益霞，刘明伟.基于MATLAB的机构位置问题的牛顿法数值求解[J].湖南工程学院学报，2005,15(4):38-40

[7]李骏，程珩.环锤式破碎机动力学分析及强度校核[J]. 煤矿机械，2013,34(04)：33-35