优化习题设计,让课堂练习也生动
2016-01-15虞敏
虞敏

练习是数学教学十分重要的环节,新授的内容需要通过练习来消化、巩固,从而进一步掌握数学技能和发展数学思维。数学教学中,老师一般会在新授结束以后安排学生做练习。相对于新授环节而言,练习环节容易变得枯燥。教材中的许多习题与例题的类型相似,都是新知的巩固,因此,也就失去了新授环节的新鲜感和挑战性。如果我们在练习环节总是依照教材编排,采用一题一题地练习,一题一题地交流,或是学生先练习再整体校对,练习的形式就会变得单一呆板。学生往往一到练习环节就提不起精神,这对于练习的效果会产生很大的影响。因此,教师需要在习题的设计上求变,让习题“活”起来。
一、习题信息“藏起来”
解决问题的设计中加入图片、对话以后,与纯文字叙述相比,形式更加活泼。贴近了学
生的现实生活,容易被学生喜欢和接受。图片、对话的作用又不仅限于激发学生练习的兴趣,因为它们本身也蕴含了数学信息。
(一)信息藏进图片中
在三上《有余数除法》的教学中,有道解决问题的题目是这样的:“有20个纽扣,每件上衣需要钉3个纽扣,可以钉几件上衣,还剩几个?”这是一道纯文字叙述的题目。我们可以进行改编,设计这样的题目(如右图):“每件上衣需要钉3个纽扣”这个条件没有通过文字的形式告诉学生,而是需要学生自己去观察、去发现。这样设计以后,图片本身也就成了学生解题需要的一个数学信息了。
(二)信息藏进对话里
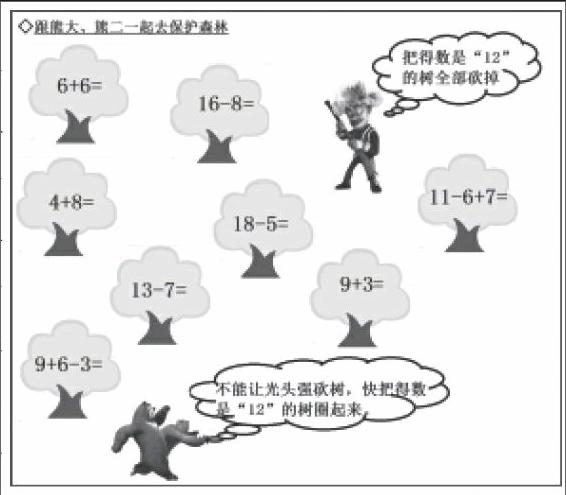
学完《20以内的退位减法》以后,需要对20以内的加减计算进行练习,以提高学生迅速、正确进行口算的能力。我们可以把这些计算题融于对话之中,设计出对话性的练习(如右图)。《熊出没》是儿童非常熟悉的动画片,本题设计了一个“跟熊大、熊二一起去保护森林”的情境。光头强要把得数是“12”的树全部砍掉,熊大、熊二得知了这个消息以后,要把得数是“12”的树保护起来,邀请同学们跟着他们去完成这一个“圈”的任务。
习题中将“把得数是12的树全部砍光”和“把得数是12的树圈起来”2个信息藏在了对话之中。光头强、熊大和熊二深受儿童喜爱,自然可以一下子吸引学生的眼球。原本略显枯燥的计算练习,在学生眼里也变得有趣起来。
在习题设计的时候,我们可以把一些数学信息“藏起来”,让学生自己去寻找。生活中的数学信息总是根据我们自己的需要去寻找的,因此,这样的习题更加贴近学生的生活实际,学生也更加有解题的兴趣。
二、习题有机“串起来”
新授结束以后,我们一般会安排相关的练习。这些习题是根据一定的目标,精挑细选产生的。但是,对于学生而言,如果每次都是一题接着一题地练习,容易感到疲劳,影响练习的效果。教师可以寻找题目之间的相关性,把零散的习题“串起来”。
(一)设计大情境
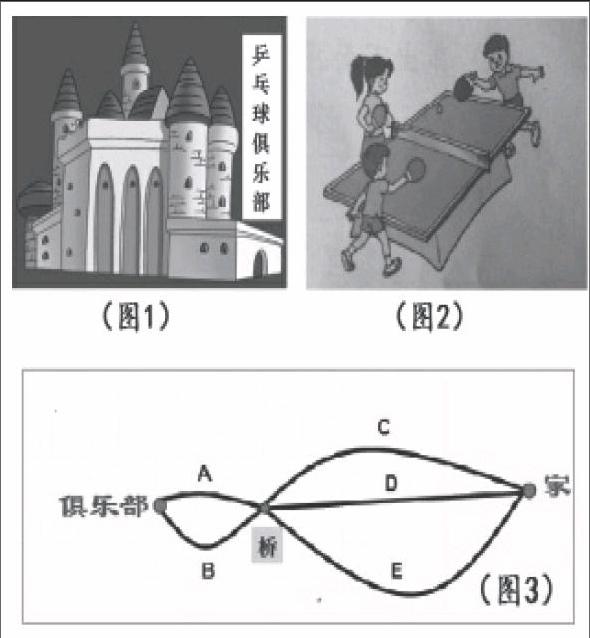
比如二上《排列与组合》的教学中,新授结束以后,可以设计这样的习题串(如右图):先呈现图1:毛毛去乒乓球俱乐部打乒乓,门票需要5元(毛毛有1张5元、2张二元和5张一元),他可以怎样付钱?第一问题解决以后,再呈现图2:进入乒乓球俱乐部以后,毛毛找到了2位好朋友,他们要一起玩。结果,他们每2人进行了一场比赛,他们一共比了几场?解决了第二个问题以后,最后呈现图3:打完乒乓以后,毛毛要回家了,他回家要经过一座桥,从俱乐部到家可以有几种不同的走法?原本独立的3个习题,通过毛毛去俱乐部打乒乓这样一个大情境串联起来,从买门票、打乒乓到选择回家的路,引出一系列的问题,使练习环节也变得活泼起来,学生解决问题的欲望被激发了出来。
练习设计中,教师可以结合一些学生熟悉的生活情境,选择生动有趣的素材,把一个个情境构成一个习题串。通过一个大的情境,一环接着一环,让学生随着情境的展开解决一个个问题,增强练习对学生的吸引力。
(二)组成综合题
数学习题的设计要突出数学知识之间的联系。设计习题的时候,我们可以将一些相关知识点的习题有机组合在一起,设计出具有挑战性的综合题。
比如在四下《三角形的单元复习》一课中,我们既需要复习三角形边的知识,又要复习三角形角的知识,而三角形的角和边之间存在密切的联系。因此,我们可以将角的复习和边的复习有机整合在一起。我设计了这样一个练习题(如右图),学生在这一习题中不断地在思考角与边之间的关系。(1)口算得出∠ACB=60°,从而根据角的度数判断出△ABC是一个等边三角形。(2)根据△ABC是一个等边三角形,得出AC这条边的长度是2厘米,因为边CD也是2厘米,从而得出△ACD是一个等腰三角形。(3)根据根据∠ACB=60°和平角是180°,得出∠ACD=120°。(4)根据△ACD是一个等腰三角形和∠ACD=120°得出∠CAD=30°。(5)根据∠CAD=30°和∠BAC=60°得出∠BAD=90°,判断出△ABD是一个直角三角形。
在这一个习题中既有“三角形分类”知识的复习,也有“三角形内角和”知识的复习,更为重要的是将两者紧密地结合在一起。学生经历根据角的特征得出边的特征,根据边的特征来推断出角的特征这样“来回穿梭”的过程。这样的练习有助于深刻地理解和掌握知识间的内在联系和本质规律,完善学生的认知结构,提高学生分析问题和解决问题的能力。
(三)编排新顺序
人教版练习都以序号为顺序编排,从表面上看都是分开的。细细想来,有的练习虽然没有编排在一起,但是它们是紧密相连的,如果串联在一起可以整合知识,起到了相互补充的作用,可以发挥更大的价值。
比如五上《练习一》中,先让学生尝试练习第10题(如下图)。学生在计算的过程发现,第一个表格中的积都大于第一个因数,而第二个表格中的积都小于第一个因数。然后,引导学生进一步理解,因为1倍正好等于本身,乘上超过1倍的数,积自然比原来的数大;乘上不到1倍的数,积也就比原来的数小了。endprint
接着让学生应用刚才总结的规律,解决第12小题。(如右图),完成以后,追问:“你是怎样想的?”引导学生大致总结出规律:“一个数(0除外)乘大于1的数,积比原来的数大。一个数(0除外)乘小于1的数,积比原来的数小。”
通过这样的串联,把原本单独练习的2道题目整合在一起,学生经历了一个尝试、验证、获得并应用规律的过程,对规律价值的感受更加深刻。
三、习题游戏“做起来”
喜欢游戏是孩子的天性,把游戏和教学结合起来,使其融为一体,相互促进,就会收到事半功倍的效果。
(一)师生互动猜一猜
比如五下《分数的意义》教学中,特级教师朱国荣设计了一个游戏环节:朱老师拿着一个装有小奖品(本子)的大信封。游戏环节一:朱老师先取出2本,告诉学生,这2本是带来本子的1/5,让学生猜大信封里一共有多少本子?学生猜到是10本。然后朱老师每次取2本,结果学生表示的分数都不相同。朱老师发问:“刚才这2本是1/5,现在这2本是1/4,这是什么原因呀?”引导学生关注单位“1”发生了变化以后,取同样的数量,表示出的分数是不一样的。游戏环节二:当袋子里只剩下2本的时候,朱老师说:“如果我要拿出这2本的1/2,我要拿几本?”“这1本(16页),我能拿它的1/2吗?”“取了8页以后,还要拿1/2?”……朱老师不断地取着剩下部分的1/2。并与学生一起理解“一日之锥,日取其半,万世不竭”含义。学生发现单位“1”发生了变化以后,取出的“1/2”表示的数量也是不一样的。
《分数意义》的教学中,教学的重点是引导学生关注单位“1”,关注“把谁看做了一个整体”,这对于后续分数解决问题的学习至关重要。朱老师通过一个小小的游戏,让学生加深了对单位“1”的理解,体会到确定单位“1”的重要性。同时,在一节课的最后环节学生依然热情高涨,思维活跃,朱老师精心设计的小游戏功不可没。
(二)生生互动抽一抽
比如学完了9的乘法口诀以后,需要设计一些练习来提高学生迅速、正确进行乘法口算的能力。我们可以将口算题与学生熟悉的纸牌游戏结合起来,设计一个“夺牌小高手”游戏:四人小组合作,其中一位同学从18张牌中(1~9各2张)中任意抽取2张,报出一道题目,其余3位学生抢答。比如:抽到“7”和“8”,可以随机出加法题“7+8”、减法题“8-7”或者乘法题“7×8”。答得又对又快的同学拿走这2张牌,最后手中牌最多的同学获得“夺牌小高手”。
学生在出题和抢答的过程中巩固了乘法口诀,提高了口算的能力。同时,在游戏中练习,避免了单纯的计算训练,学生乐于算、乐于练,练习的环节也变得趣味盎然。
总之,设计习题的时候我们既要深研教材,准确把握每道题的意图,避免随心所欲地更改习题。同时,又要根据学生的年龄特点和本班学生的实际情况,设计出形式多样,有思维含量的习题,让习题变得生动起来。通过变换习题的形式,让学生对练习环节一样充满期待,从而激发起学生练习的热情,提升学生解决问题的能力。endprint
