分层有限元模型下层合板声功率优化设计

第一作者吴锦武男，博士，教授，1976年9月生

分层有限元模型下层合板声功率优化设计

吴锦武，彭文辉，赵飞

(南昌航空大学飞行器工程学院，南昌330063)

摘要：基于遗传算法对层合板结构辐射声功率最小化进行铺设角优化；利用分层有限元模型求解层合板固有频率及振速分布；通过声辐射模态理论计算结构辐射声功率。以铺设角作为设计变量、辐射声功率作为优化变量，分别以某4层、8层层合板结构为例，研究不同频率时声功率最小化对应的优化铺设角。数值分析结果表明，在同一优化铺设角下，优化后第一阶声功率与辐射总声功率差别不大；对相同层合板结构而言，随频率增加声功率优化量增大；相同厚度下层合板铺设层越多声辐射功率优化量越小。

关键词：遗传算法；声功率；分层有限元；复合层合板

基金项目：国家自然科学

收稿日期：2014-04-17修改稿收到日期：2014-08-14

中图分类号:TB332；TH113.1文献标志码：A

基金项目：国家973计划资助(2011CB013405)；国家杰出青年科学基金资助(51125023)

Optimal design of acoustic power of laminated composite plate based on layer-wise FEM

WUJin-wu,PENGWen-hui,ZHAOFei(School of Aircraft Engineering, Nanchang HangKong University, Nanchang 330063, China)

Abstract:An optimization method to minimize the sound power of laminated composite plate based on genetic algorithm was presented. A layerwise finite element model was imposed to determine the natural frequencies and velocity distributions of laminated composite plates. Based on the theory of acoustic radiation mode, the radiated sound power was calculated. A four-layer and an eight-layer laminated plate were used as examples, the fiber orientation angles were taken as design variables and the minimization of sound power was chosen as design objective. The optimal orientation angles to achieve sound power minimization were discussed under different frequencies. The numerical simulations show that the first order sound power and the total sound power are basically identical under the same optimum orientation angle. For laminated composite plates with the same structure, the optimal amount of radiated sound power increases with the increase of vibration frequency. And for laminated composite plates, with the same thickness, the optimal amount of radiated sound power is smaller, the more the layer number of the plate.

Key words:genetic algorithm; sound power; layerwise finite element; laminated composite plates

复合材料因比强度大、比刚度高、性能可设计等特点广泛用于航空航天、汽车、船舶等领域。复合材料层合板结构减震降噪优化设计颇受关注[1-8]，其设计分析、铺层优化方法已成重要研究课题。

减振优化设计，针对优化层合板结构铺设角度主要分两类：①若外激励频率不高，通过提高基频可减少共振可能性，此时层合板结构优化以基频最大化为优化目标函数。罗志军等[1]以第一阶固有频率最大化为目标函数，以铺层顺序为设计变量，将遗传算法与有限元软件相结合，对层合板铺层顺序进行优化。为获得层合板最大临界屈曲载荷系数及最大固有基频，唐文艳等[2]采用改进的遗传算法将铺层角度作为离散变量对层合板铺层顺序优化设计。晏飞等[3]利用遗传算法针对复合材料层合板基频、铺设角度等优化研究。②若外部激励频率过高，常用增大相邻两阶固有频率间隔减少产生共振的风险。Adali等[4]以最大基频、最高频率间隔为设计变量在自由振动下确定对称层合板最佳铺层顺序，但为节省计算时间，其将纤维铺设方向限制于预选的4个不同角度。

声优化设计，以层合板受外激励作用的声辐射功率最小为设计变量，优化复合材料铺层顺序[5-6]。陈炉云等[7]利用遗传算法以声辐射功率最小化为目标函数，对层合板铺设层数、厚度及铺层顺序等进行集成优化设计。

以上研究一般基于等效单层板理论分析其动力学特性。由于该单层板理论分析层合板结构振动特性时忽略板横向剪切变形，会导致位移、应力偏小、固有频率偏高。本文拟通过分层理论结合有限元方法分析固有频率，在考虑层合板结构振动前提下结合声辐射模态理论，采用遗传算法，以辐射声功率最小化为目标函数对复合材料层合板铺设角度铺层顺序进行优化设计。

1结构动力响应

基于分层理论沿板厚方向采用分层插值，层合板结构物理模型见图1。

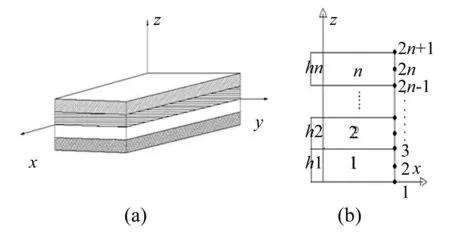
图1　层合板结构坐标图 Fig.1 Laminated plate geometry and coordinate system

层合板结构位移场[9]可表示为

(1)

式中：U(x,y,z,t)，V(x,y,z,t)，W(x,y,z,t)分别为x,y,z方向位移；n为铺设层数；2n+1为插值面数；ui(x,y,t)，vi(x,y,t)，wi(x,y,t)为第i个插值平面内hj方向位移；Ψ1(z)为沿厚度方向离散化平面内位移全局插值函数,取值为

(2)

式中：zk为第k个插值层坐标；φ1i,φ2i为沿厚度方

向离散化横向位移全局插值函数，分别等于

(3)

(4)

式中：vi(x,y,t)为层合板第j个铺设层厚度；wi(x,y,t)为板厚局部坐标。

据有限元理论，采用四节点矩形单元，式(1)中ui(x,y,t),vi(x,y,t)，wi(x,y,t)可表示为

(5)

式中：m为有限元单元节点数；Nk(x,y)为形函数表达式；uk,vk,wk为有限元节点k处x,y,z坐标；T(t)为时间函数。

将式(5)及节点形函数代入式(1)，得单元形函数矩阵N为

(6)

据弹性力学位移-应变关系，单元应变矩阵为

(7)

式中：

(8)

正交材料应力应变关系矩阵为

[σ]=D[ε]

(9)

(10)

据有限元理论，层合板结构动力学方程为

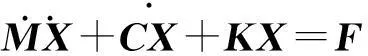
(11)

式中：M为单元质量矩阵；K为单元刚度矩阵； C为阻尼矩阵；F为单元等效节点力矩阵。

2结构辐射声功率

设振动平板表面积S置于无穷大刚性障板上，以圆频率ω向上半空间辐射声。声场介质密度为ρ,声速为c。振动板表面分成J个等面积单元。设每个单元长度远小于声波波长，其法向速度构成速度向量为U(ω)。总声功率W(ω)[10]可表示为

(12)

式中：上标H为复数共轭转置；R为阻抗矩阵；W1(ω)为第一阶声辐射模态对应辐射声功率。

由声辐射模态理论[11]可知，低频时板结构前几阶声辐射模态声功率占总声功率绝大部分，其中第一阶声功率W1(ω)占总辐射声功率比重最大。本文以第一阶辐射声功率及总声功率为目标函数对铺设角度进行优化，比较最优值。

3遗传算法

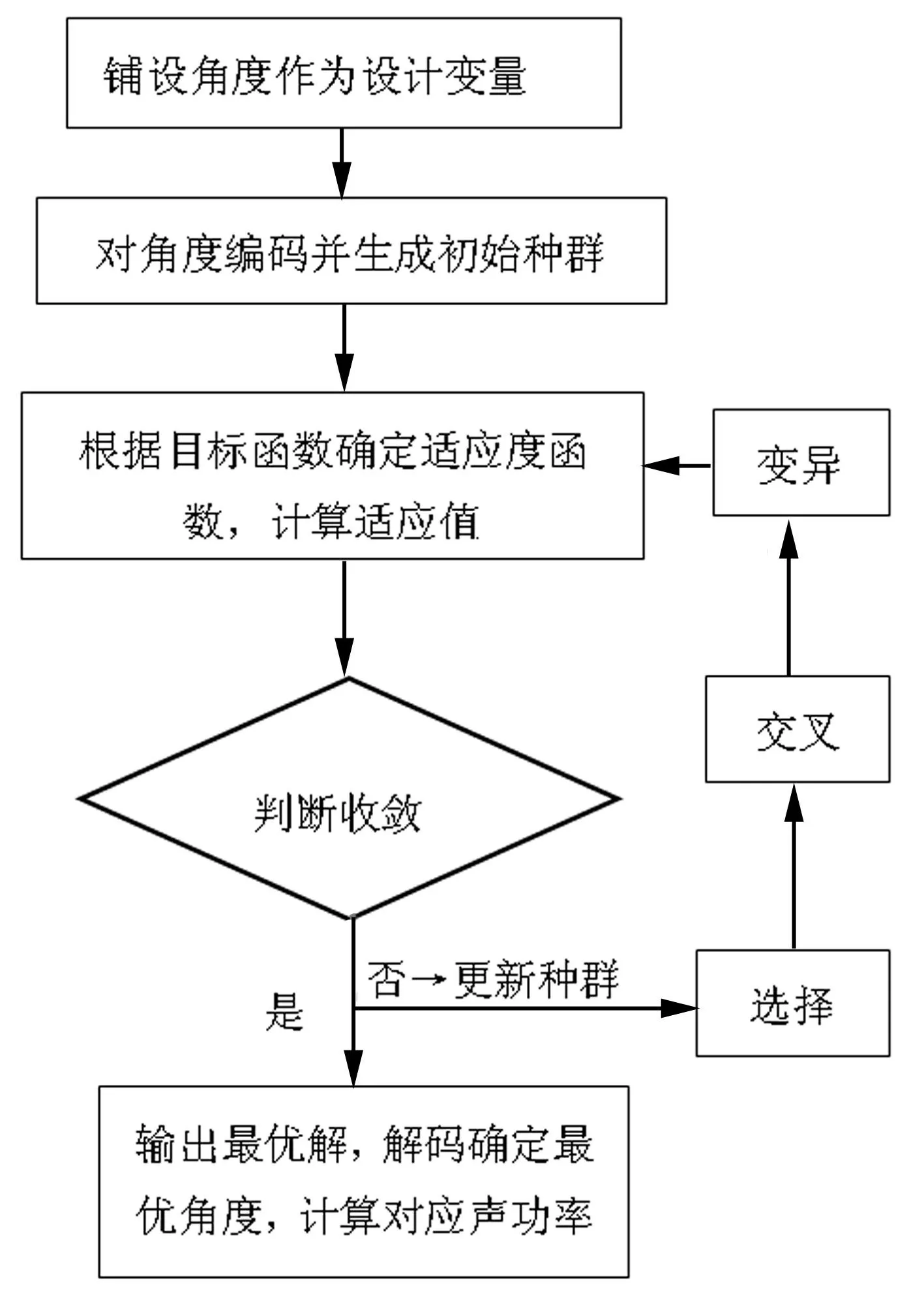
图2　声功率最小化遗传算法计算流程图 Fig.2 Genetic algorithm frame diagram of sound power minimization

诸多工程应用中，层合板结构纤维铺设角度常局限于一定范围内，如0，30，45，90等，层合板铺层顺序优化即成为离散变量优化问题， 且存在多个极值点，用传统优化求解方法较困难。较传统优化方法遗传算法具有以决策变量编码作为运算对象，可处理规模较大问题；可进行多点搜索，具有良好的全局搜索能力；直接以目标函数值作为搜索信息，可用于不连续变量等优点[12]。本文利用matlab遗传算法工具箱[13]求解复合材料层合板铺层顺序优化问题。用整数编码方式对层合板铺层角度编码。编码串中每个数字代表一个铺层，称为基因。基因在基因串上的排列顺序代表层合板铺层顺序，如4层板[-30°/-60°/60°/30°]的对应基因码为2/1/5/4。标准遗传算法中操作包括选择、交叉、变异等。引用标准遗传算法操作方法产生新种群。优化目标分别为基频、频带最大化频率及声功率最小化。遗传算法流程见图2。

4结构-频率优化

为有效避免层合板结构共振，研究结构固有频率。本文规定频率参数Ω[14]为

(13)

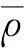
(14)

式中：ν12，ν21为泊松比；E2为垂直于纤维方向弹性模量；h为层合板总厚度；D0不随层合板铺层角度变化。

针对层合板固有频率，取最大相邻阶固有频率间隔作为优化变量。结构-频率优化问题可写成

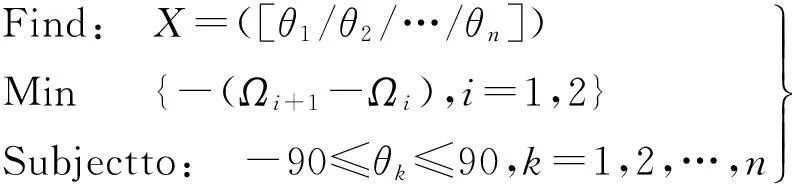
(15)

式中：θk为第k层层合板纤维铺设角度；Ωi为层合板第i阶固有频率对应频率参数。

由于遗传算法只能求解目标函数最小值问题，因此式(15)取Ωi+1([θ1/θ2/…/θn])-Ωi([θ1/θ2/…/θn])的相反数。

采用第一、二阶无量纲固有频率间隔Ω12作为优化变量，定义铺设角度铺层顺序为设计变量,铺设角度选离散形式(-45°,0°,45°,90°),分别优化4，8，12，16层对称长宽比为2的复合材料层合板铺层顺序；并与文献[13]结果对比。层合板性能参数为：E1=138 GPa，E2=E3=8.96 GPa，G21=G23=G31=7.1 GPa，ν12=0.3，不考虑结构阻尼。层合板铺设角度为[θ1/θ2/…/θn]，θ1为最外层铺设角度，θn为最内层靠近对称面一层铺设角度，层合板每层厚度相同。采用前二阶无量纲固有频率间隔Ω12作为优化变量时，优化结果见表1。由表1看出，①随相同厚度下层合板铺设层数增加Ω12值呈增加趋势；②相同铺设层数下本文所得最优解优于文献[14]，因该文献为简便忽略层合板拉弯耦合作用，且为避免过多错误施加额外弯曲刚度；而本文既未忽略层合板耦合刚度亦未施加额外弯曲刚度。

表1　长宽比为2矩形层合板铺设角度优化结果

5结构-声辐射优化

由式(11)知，通过改变层合板铺层角度可改变结构层合板表面的法向振速分布，从而影响其声辐射功率。选声辐射功率作为优化变量，层合板结构-声辐射优化模型数学表达式为

(16)

式中：W(ωp)为激励频率等于ωp时层合板总声辐射功率；f1为层合板基频。

分别以4、8层复合材料层合板为例，层合板性能参数为：长a=0.348 0 m，宽b=0.304 8 m，厚度h=0.002m，E1=181 GPa，E2=E3=10.3 GPa，G21=G23=G31=7.17 GPa，ν12=0.28，阻尼比=0.05；固定激励频率分别为低频ωp=200 Hz，高频ωp=500 Hz，激励力为1 N，作用点位于板结构中心，采用遗传算法优化层合板铺层顺序，初始角度分别为[0°]4、[0°]8。激励频率ωp=200 Hz，4、8层板铺层顺序优化结果见表2、表3，对应铺层顺序下4、8层铺设层合板优化辐射总声功率级曲线对比见图3、图4。由两表知，激励力频率200 Hz时，相同层数层合板结构优化后第一阶声辐射功率与总辐射功率基本相同。说明低频时第一阶声功率占总声功率绝大多数。由两图看出，激励力频率200 Hz时，4层复合材料层合板结构最优角度为[0°/-45°/30°/90°]，结构声功率优化前后降低量为1.9 dB；而8层层合板最优角度为[90°2/-30°2/-15°/0°3]，声功率降低量达1.1 dB。

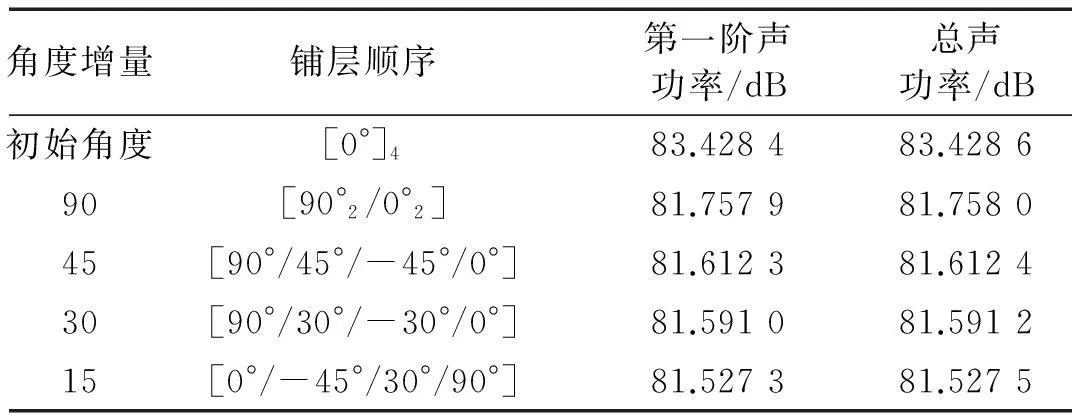
表2　激励频率200 Hz四层板铺层顺序优化结果

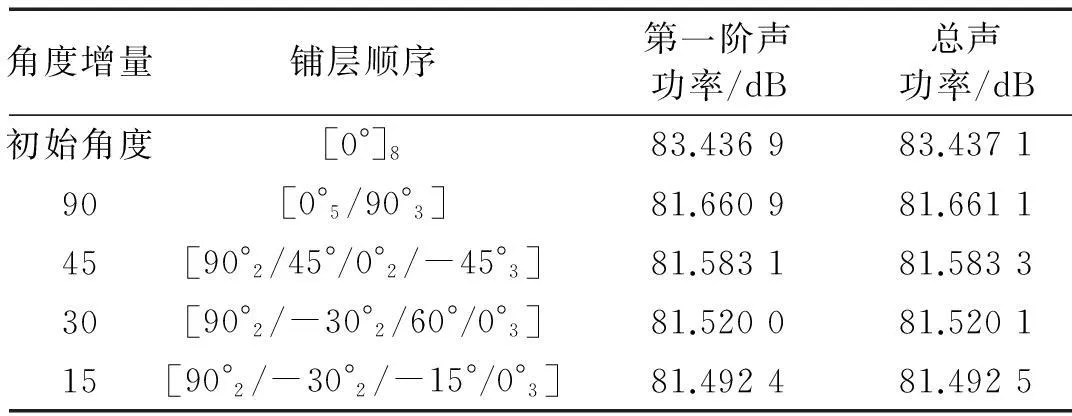
表3　激励频率200 Hz八层板铺层顺序优化结果

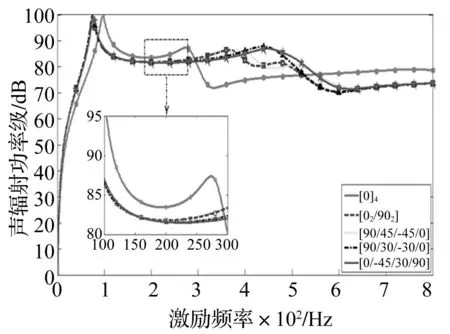
图3　四层层合板声功率优化结果(ω p=200 Hz) Fig.3 Optimum acoustic power of four layer plate (ω p=200 Hz)

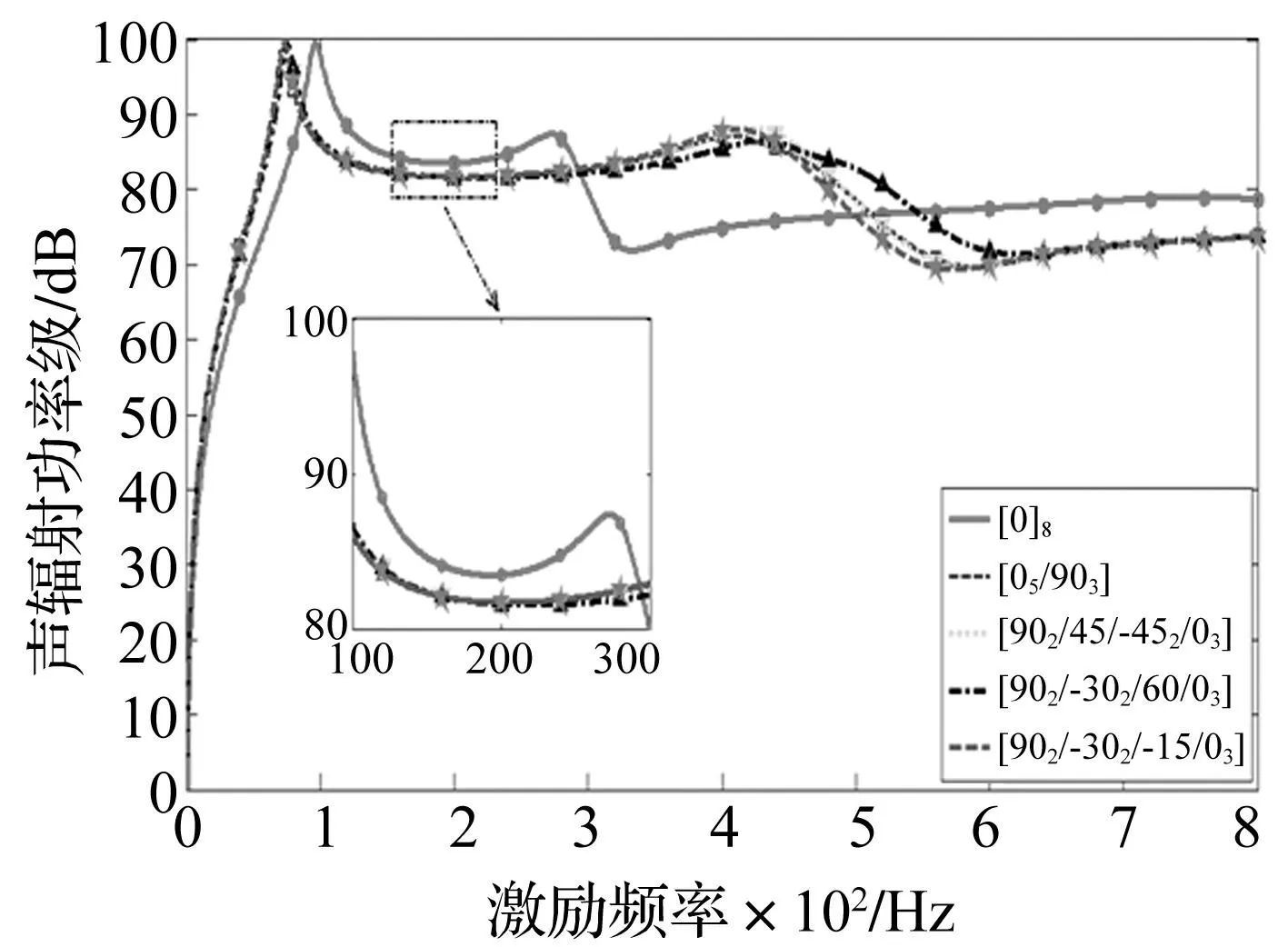
图4　八层层合板声功率优化结果(ω p=200 Hz) Fig.4 Optimum acoustic power of eight layer plate (ω p=200 Hz)

随激励力频率增高，对应激励频率ωp=500 Hz四、八层板铺层顺序优化结果见表4、表5，ωp= 500 Hz对应铺层顺序下4、8层铺设层合板优化总声功率级曲线对比见图5、图6。由两表可知，随频率增高，激励力频率为500 Hz时相同层数层合板结构优化后第一阶声辐射功率与总辐射功率差别不大，小于1.1 dB。因此优化第一阶声功率与辐射总声功率效果基本相同。由两图看出，激励力频率为500 Hz时4层层合板结构最优角度为[-30°/-15°/75°/45°]，声功率优化前后降低量为6.2 dB。8层层合板最优角度为[90°2/0°2/90°2/0°/90°]，声功率降低量达3.2 dB。

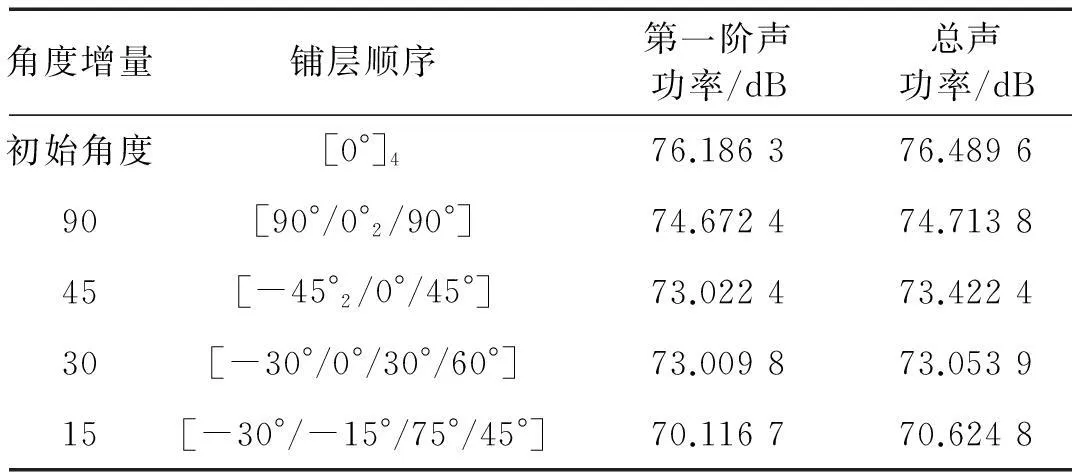
表4　激励频率500 Hz四层板铺层顺序优化结果

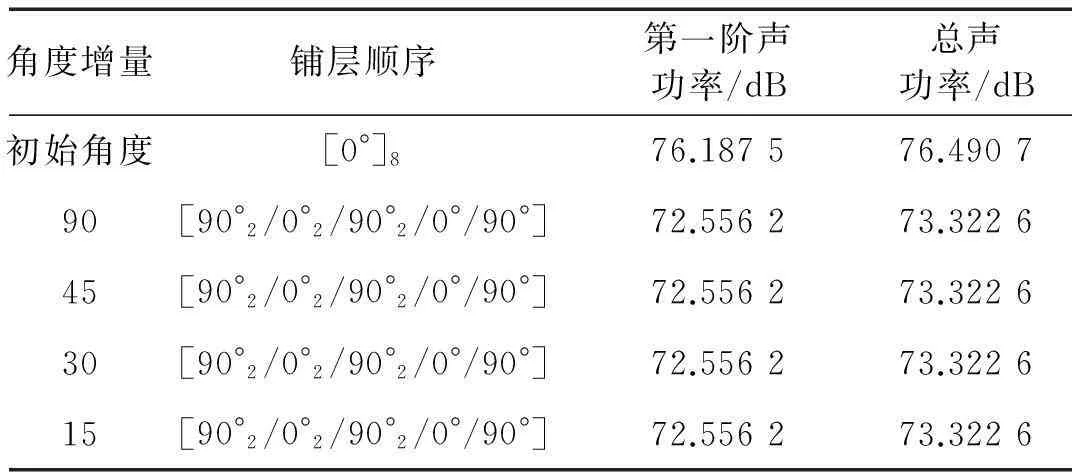
表5　激励频率500 Hz八层板铺层顺序优化结果

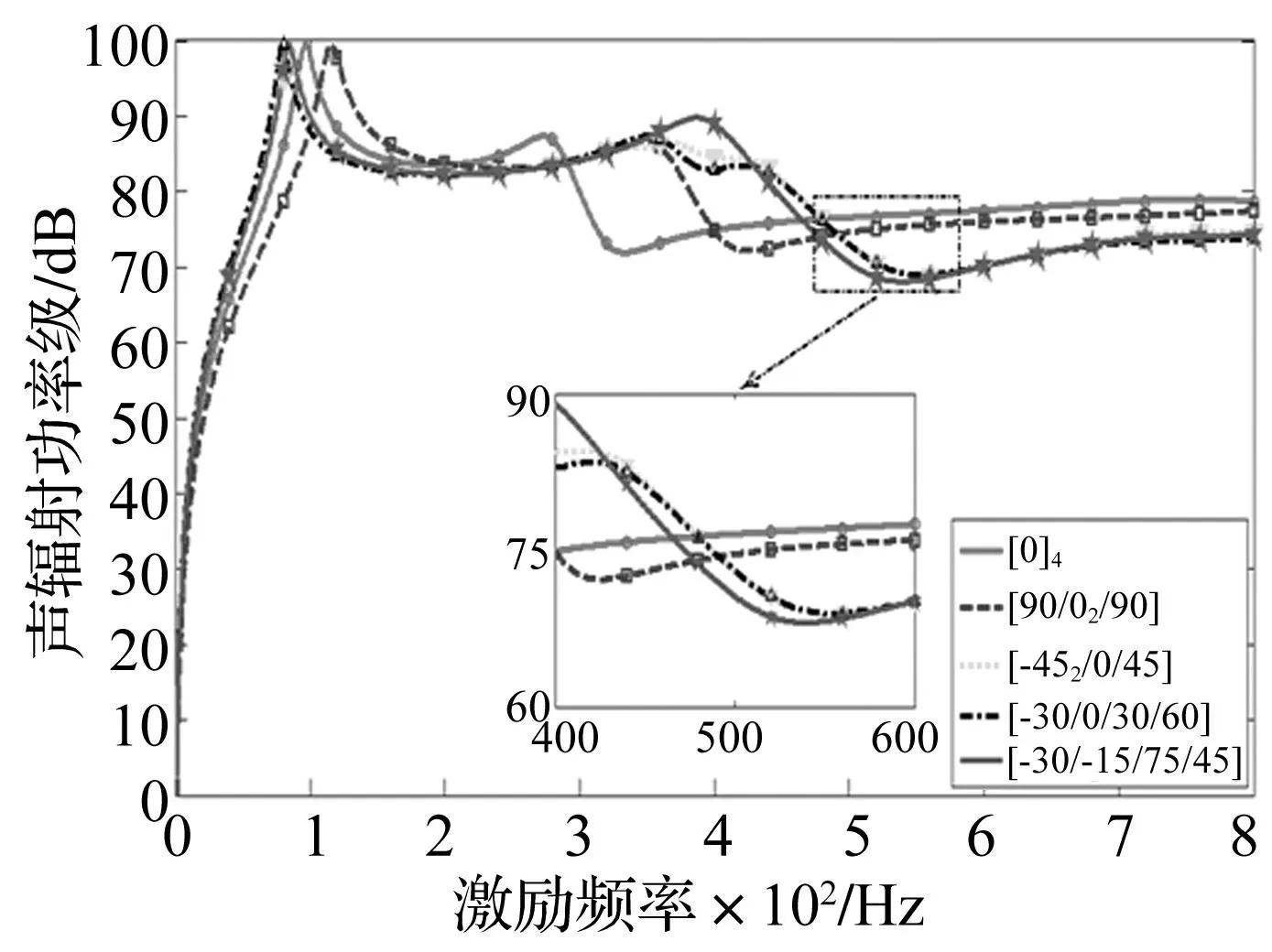
图5　四层层合板声功率优化结果(ω p=500 Hz) Fig.5 Optimum acoustic power of four layer plate (ω p=500 Hz)

综上所述，通过优化铺设角度，层合板结构声辐射功率优化效果明显，与复合材料层合板结构各向异性有关。同厚度的8层层合板不同激励频率下声辐射功率级均小于4层层合板，因随层数增加整个板结构各项异性有所减弱。

图6　八层层合板声功率优化结果(ω p=500 Hz) Fig.6 Optimum acoustic power of eight layer plate (ω p =500 Hz)

6结论

(1)基于分层有限元模型分析层合板结构的振动特性，可有效避免复合材料层合板结构产生共振。

(2)据声辐射模态理论，通过分层有限元模型可获得层合板结构声功率。通过用遗传算法分析层合板结构第一阶与总声功率知，优化第一阶声功率与总声功率效果相当。

(3)层合板结构层数相同时，随外激励力频率增加优化效果提高；板越厚频率越低，声功率优化效果越好。

参考文献

[1]罗志军,乔新. 基于遗传算法的复合材料层压板固有频率的铺层顺序优化[J]. 复合材料学报,1997,14(4):114-118.

LUO Zhi-jun, QIAO Xin. Optimization of ply stacking sequence for natural frequencies of composite laminates by genetic algorithm [J]. Acta Materiae Compositae Sinica, 1997, 14(4):114-118.

[2]唐文艳,顾元宪,赵国忠.复合材料层合板铺层顺序优化遗传算法[J].大连理工大学学报,2004,44(2): 186-189.

TANG Wen-yan,GU Yuan-xian, ZHAO Guo-zhong. Stacking-sequence optimization of composite laminated plates by genetic algorithm[J]. Journal of Dalian University of Technology,2004, 44(2): 186-189.

[3]晏飞,李为吉.基于自适应遗传算法的复合材料层合板铺层顺序优化设计[J].西北工业大学学报,2001,19(l):156-159.

YAN Fei, LI Wei-ji. A stacking sequence optimization method of composite laminated panel based on an adaptive genetic algorithm [J]. Journal of Northwestern Polytechnical University,2001, 19(l):156-159.

[4]Adali S, Verijenko V E. Optimum stacking sequence design of symmetric hybrid laminates undergoing free vibrations[J]. Composite Structures, 2001, 54(3): 131-138.

[5]Du J, Olhoff N. Minimization of sound radiation from vibrating bi-material structures using topology optimization[J]. Structural and Multidisciplinary Optimization, 2007,33(5): 305-321.

[6]Duhring M B, Jensen J S, Sigmund O. Acoustic design by topology optimization [J]. Journal of Sound and Vibration, 2008, 317(5): 557-575.

[7]陈炉云,张裕芳. 基于遗传算法的复合材料结构-声辐射优化研究[J]. 复合材料学报, 2012,29(3): 203-207.

CHEN Lu-yun,ZHANG Yu-fang. Composite material structural-acoustic optimization on genetic algorithm[J]. Acta Materiae Compositae Sinica,2012, 29(3): 203-207.

[8]郑玲,祝乔飞.约束阻尼板结构振动声辐射优化[J].振动与冲击,2014,33(5):91-96.

ZHENG Ling,ZHU Qiao-fei.Topology optimization for acoustic radiation of a comstraint damping plate[J]. Journal of Vibration and Shock, 2014,33(5):91-96.

[9]Reddy J N. Theories and computational models for composite laminate [J]. Applied Mechanics Reviews, 2004, 47(6):147-169.

[10]Elliott S J, Johnson M E. Radiation modes and the active control of sound power [J]. The Journal of the Acoustical Society ofAmerica, 1993, 94(4): 2194-2204.

[11]姜哲.声辐射问题中的模态分析Ⅰ:理论[J].声学学报, 2004, 29(4):373-378.

JIANG Zhe. A modal analysis for the acoustic radiation problem: I, theory[J]. Acta Acustica,2004, 29(4):373-378.

[12]李敏强,寇纪淞,林丹,等. 遗传算法的基本理论与应用[M]. 北京:科学出版社,2002.

[13]雷英杰. Matlab遗传算法工具箱及应用[M].西安:西安电子科技大学出版社, 2005.

[14]Nemeth M P. Importance of anisotropy on buckling of compression-loaded symmetric composite plates[J]. American Institute of Aeronautics and Astronautics Journal,1986,24(11):1831-1835.