四角点固定支承矩形板固有特性研究
2016-01-15李郑发,曹登庆,张迎春
四角点固定支承矩形板固有特性研究
李郑发1,2,3,曹登庆2,张迎春1,3
(1.深圳航天科技创新技术研究院,广东深圳518057; 2.哈尔滨工业大学航天学院,哈尔滨150001;3. 深圳航天东方红海特卫星有限公司,广东深圳518054)
摘要:四角点固定支承矩形板横向振动固有特性的研究对其实际应用及故障诊断具有重要意义。基于能量守恒原理并结合固定支承点处的约束条件建立四角点固定支承矩形板横向振动的拉格朗日方程。采用幂级数多项式来描述其振型函数,根据Rayleigh-Ritz理论推导出四角点固定支承矩形板的横向振动频率方程;由频率方程给出了不同长/宽比矩形板基频的理论计算结果,并应用该方法获得了四角点简支矩形板的频率方程。对典型算例的理论计算结果和有限元分析结果进行比较和分析,给出便于工程应用求解其基频的近似计算式;通过试验研究表明理论计算结果与有限元分析结果和试验结果具有较好的一致性。
关键词:矩形板;点支承;基频;Rayleigh-Ritz方法;Lagrange乘子
中图分类号:O326
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.19.015
Abstract:The natural characteristics of a rectangular plate clamped at 4 corner points are of importance in its application and fault diagnosis. Firstly, its Lagrange equation of transverse vibration based on the principle of energy conservation under constraint conditions of support locations was established to analyze its free vibration problem. Secondly, the frequency equation of the rectangular plate was obtained using Rayleigh-Ritz method with simple polynomials as its modal functions. Finally, the fundamental frequencies were gained for different side ratios according to the theoretical results of the rectangular plates, they were compared with those obtained using the finite element method. In order to get the fundamental frequencies conveniently, approximate expressions were deduced for a typical plate with certain geometrical parameters and material constants in practical engineering. It was shown that the theoretical results agree well with those obtained using the finite element method and the test data.
Natural characteristics of rectangular plates clamped at 4 corner points
LIZheng-fa1,2,3,CAODeng-qing2,ZHANGYing-chun1,3(1. Shenzhen Academy of Aerospace Technology, Shenzhen 518057, China;2. The School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;3. Shenzhen Aerospace Dongfanghong HT Satellite Ltd. CAST, Shenzhen 518054, China)
Key words:rectangular plates;point supports;fundamental frequency;Rayleigh-Ritz method;Lagrangian multiplier
板的振动问题一直受到科学和工程界的重视,板在不同边界条下的振动问题仍然是振动研究领域的热点之一。四点支承矩形板在建筑、航天、电子等工程领域中有着广泛的应用,如四点支承的玻璃幕墙结构、四点支承的电路板结构、以及四点支承的太阳翼结构等。其中四角点支承矩形板结构形式在工程中应用尤为广泛,研究其横向振动固有特性对其工程应用及故障诊断具有非常重要的意义。对简单边界条件的矩形板横向振动固有频率可以获得其解析解,如四边为简支、四边固支或者有一对边简支等情况。对于其他复杂边界条件,由于在数学方面的困难,很少得到解析解。多年来,国内外学者在求解点支承薄板自由振动方面进行了大量的研究工作:如Gorman[1-3]基于薄板振动问题的经典解析解,提出采用叠加法求解点支承矩形板的振动问题。Huang[4]利用离散分析方法研究点支承矩形板自由振动问题。通过引入狄拉克δ函数建立了点支承板弯曲问题的基本微分方程,将微分方程转化为积分方程,并利用格林函数通过数值积分得到其自由振动特征方程,讨论了点支持、板厚度以及长宽比对于振动频率的影响。Bapat[5]采用柔度函数法分析了位于板自由边界和内部多点支承矩形板的振动问题。该方法是在自由边界或内部支点处添加一个虚拟的弹性约束条件,并构造一个柔度函数满足其约束处的位移边界条件。Narita[6]利用双幂级数试函数,支承点的约束条件由Lagrange乘子引入,并根据Ritz法分析了对称四点支承正交异性矩形板、带内部支承点的正交异性悬臂板和任意多支承点正交异性椭圆板的自由振动问题。王砚[7]采用无网格Galerkin法求解具有有限多个弹性支承点的矩形薄板横向振动问题。通过弹性动力学Hamilton原理的推广应用得到具有有限多个支承点的薄板横向振动方程变分式,采用无网格Galerkin方法建立横向振动方程,并得到该问题的特征方程。此外,还有学者采用分求积法、Rayleigh-Ritz法、有限差分法和有限层法等对点支承矩形薄板的振动特性作过研究,请参阅文献[8-15]。
目前对四点支承矩形板振动分析大部分局限于简单情况,但在实际工程中板固定处的连接通常偏向于刚性连接(即四点固定支承形式),而对四角点固定支承矩形板横向振动固有特性的研究还没有相关报道。本文主要围绕获得较为精确的四角点固定支承矩形板横向振动固有频率开展相关工作。首先,基于能量守恒原理并结合固定支承点处的约束条件建立四角点固定支承矩形板横向振动的拉格朗日方程;其次,采用幂指数多项式来描述其振型函数,基于Rayleigh-Ritz理论近推导四角点固定支承矩形板的横向振动频率方程;最后,给出了不同长/宽比矩形板基频的理论计算结果,并应用该方法得到四角点简支矩形板的频率方程。对典型算例理论计算结果和有限元分析结果进行了比较和分析,给出便于工程应用求解其基频的近似计算式;通过试验研究表明理论计算结果与有限元分析结果和试验结果具有较好的一致性。
1振动拉格朗日方程的建立
考虑边长分别为a,b的各向同性均质矩形板,其板的两边分别位于坐标轴ξ、ζ上(见图1)。固定支承点分别位于A,B,C和D处,四边处于自由状态。
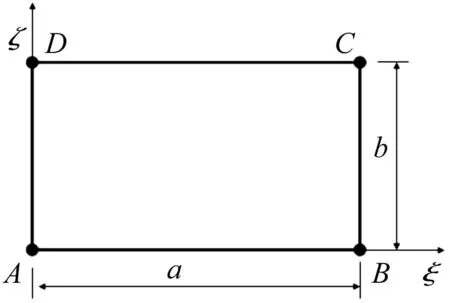
图1 四角点固定支承板 Fig.1 Sketch of a rectangular plate clamped at corner points
当板作横向振动时,其挠度函数可以表示为:
w(ξ,ζ,t)=W(ξ,ζ)sin(ωt)
(1)
式中,ω为板的振动角频率,W(ξ,ζ)为板横向振动形函数。
那么,板在横向振动过程中的动能T和势能U分别表示为:
(2)
(3)

为了便于分析,引入无量纲参数x=ξ/a、y=ζ/b。将式(1)代入式(2)和(3)整理得到结构板最大动能Tmax和板的最大变形势能Umax分别为:
(4)
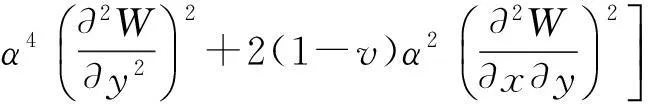
(5)
式中,α=a/b是板的长宽比,W(x,y)为其无量纲挠度函数。
由能量守恒原理,板在振动过程中最大变形势能Umax等于其最大动能Tmax得到:
Umax-Tmax=0
(6)
把式(4)和(5)代入到式(6)整理得到:
U0-ηT0=0
(7)
式中,
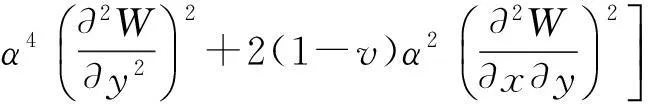
(8)
η=ρhω2a4/D
(9)
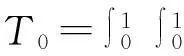
(10)
对于见图1的四角点固定支承板,其支承点A,B,C和D处应满足如下基本条件:
(1)位移条件:
W(xp,yp)=0,p=A,B,C,D
(11)
(2)转角条件:
(12)
(13)
为了便于叙述令:
(14)
2矩形板频率方程的推导
对四角点固定支承矩形板其振型函数W(x,y)可以选用如下函数表示:
(15)
式中,Amn为待定常数,φm(x)和φn(y)分别表示为:
(16)
(17)

(18)
将表达式(15)代入方程(18)得到系统的频率方程为:
(19)
式中,
(20)

(21)
(22)
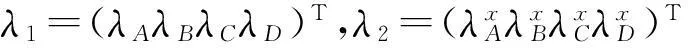
(23)
Kp=φm(xp)φn(yp),
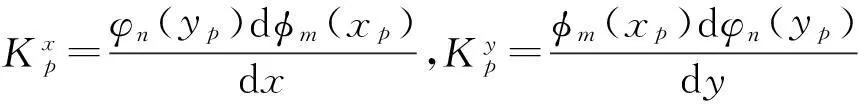
(24)
m,i=0,1,2,…,M;n,j=0,1,2,…N;p=A,B,C,D;r,s=0,1,2。
给定表达式(15)中的项数M,N后,通过方程(19)可求得参数η,从而得到系统的频率:
(25)
3数值分析与结果分析
由方程(19)求得最小特征值,并由式(25)得到系统基频fmin。从方程(19)可以看出,当系统振型函数W(x,y)多项式的项数M和N值确定后,η仅与板长宽比α和材料泊松比v有关。图2给出最小特征值ηth-fmin与α关系的理论计算曲线,其中材料泊松比v=0.3,W(x,y)多项式的项数取M=7、N=7。
由于振型函数W(x,y)选取上采用幂指数多项式,所以其项数取到一定数量时才能得到较精确的计算结果,当项数取较多时使得求解过程较为耗时。为了便于工程应用求解,由图2中的理论计算可以拟合出1≤α≤2范围内结构基频的近似计算式ηap-fmin为:
ηap-fmin=189-472e(-α/0.68),(v=0.3)
(26)

图2 长宽比α与参数η关系(四角固支) Fig.2 Side ratio α vs. parameters η (clamped at corners)
当已知结构的α值时,由方程(26)可快速获得η值。为了验证其正确性,任意选取4种不同长宽比的矩形板分别进行理论计算、采用近似公式(26)计算和有限元计算,所得结果分别列于表2,相关参数见表1。其中有限元分析采用通用Patran&Nastran前后处理和求解软件。采用4节点四边形Bending Panel单元对整板进行网划分,单元长度为0.03m;采用表1中材料参数对单元属性进行赋值;通过约束4个角点处节点的3个平动和3个转动自由度来模拟固定连接。
从表2中可以看出理论计算结果与有限元分析结果的误差在0.42%以内,能满足绝大多数工程应用的精确要求。当需要更高精度时可以增加振型函数多项式的项数进一步提高计算精度。

表1 矩形板参数
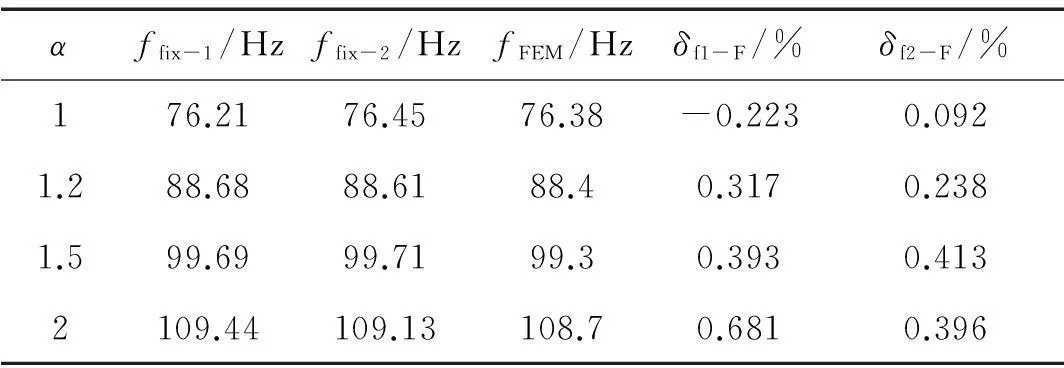
表2 基频分析结果(四角点固支)
注:表2中ffix-1为理论计算结果;ffix-2利用近似公式(26)得到的计算结果;fFEM为有限元分析结果;
上述算例表明通过频率方程(19)可以得到四角点固定支承板较精确的一阶固有频率。通过释放转角约束条件(12),应用该方法也可求解四角点简支板的固有频率。通过与方程(19)类似的推导方法可以得到四角点简支板的频率方程为:
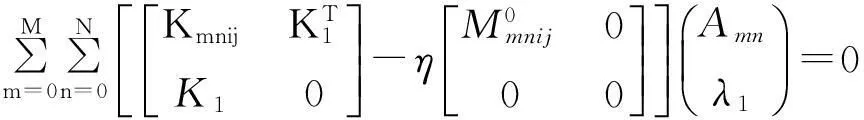
(27)
由方程(27)得到其最小特征值ηth-smin与α关系,其理论计算曲线见图3。由图3中的理论计算结果,可以拟合出长宽比在1≤α≤2范围内结构基频的近似计算式ηap-smin为:
ηap-Smin=88.35-725e(-α/0.34),(v=0.3)
(28)
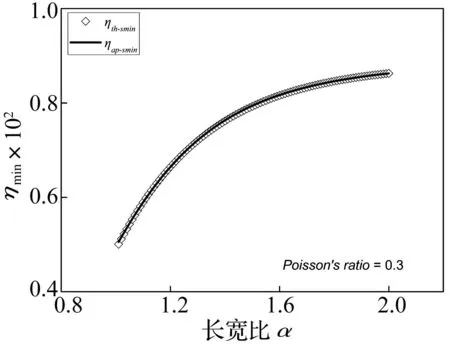
图3 长宽比α与参数η关系(四角简支) Fig.3 Side ratio α vs. parameters η (simply-supported at corners)
分别采用理论、近似公式(28)和有限元计算,所得结果列于表3。有限元分析模型采用四角点固支板有限元模型相同,约束4个角点处节点3个平动自由度来模拟简支连接。从表中可以看出理论计算结果与有限元分析结果的误差仅在±1%以内,表明该方法用于求解四角点简支板的基频也具有很好的精度。

表3 基频分析结果(四角点简支板)
4试验验证
为了验证理论分析的正确性,通过试验测试了四角点固定支承板结构的一阶固有频率。试验件所用材料是2A12T4,试样公称尺寸为230mm×200mm×2mm,试验件在四角处通过M3的钢螺钉与试验工装紧固连接,其振动测试状态见图4。振动试验在中国航天希尔公司研制的电动振动台上完成,振动台的型号为MPA3324/H1248A/BT1210;数据采集采用比利时LMS公司的LMS数据采集系统、丹麦PK公司型号为2692的电荷放大器;美国PCB公司型号为PCB35721的加速度传感器。

图4 板的振动测试状态 Fig.4 Vibration testing state of the plate
为了避免在试验件上安装过多的加速度传感器而引入附加质量,仅在试验件中间安装一个加速度传感器。采用低量级正弦扫频试验,振动方向垂直于被测板面,振动幅值为0.5g,扫频范围为10Hz~500Hz,扫描速率为2oct/min。通过其响应曲线来获得该板的一阶固有频率。
经试验获得该四角点支承板的一阶固有频率约为97.2Hz。2A12T4的材料参数:ρ=2780kg/m3、E=72GPa、v=0.3,将相关参数代入到公式(26)求得理论值为93.6Hz。理论值比试验结果低3.6Hz,其原因在于理论计算时支承点位于板的几何角点处,而试验件4个固定点仅是靠近角点处,存在一定的边界误差。此外,由于采用螺栓紧固连接使得螺钉与板接触面都被固定约束,与理论计算采用点约束相比约束明显要强。因此,试验结果比理论计算结果偏大是属于合理现象。
5结论
对四点固定支承矩形板结构固有特性的研究具有明显的工程应用背景。本文基于能量守恒原理并结合固定支承点处的约束条件建立了四角点固定支承矩形板横向振动的拉格朗日方程,并由Rayleigh-Ritz理论建立了四角点固定支承矩形板结构的频率方程。给出了便于工程应用的求解基频的近似表达式,并通过数值模拟和试验研究验证了该方法的正确性。此外,通过减少支承点处的转角约束条件,应用该方法也可求解四角点简支矩形板结构的一阶固有频率。对四角点支承矩形薄板的横向自由振动问题的研究对实际工程应用有重要的理论和实际意义。
参考文献
[1]Gorman D J. Solutions of the Levy type for the free vibration analysis of diagonally supported rectangular plates [J]. Journal of Sound and Vibration, 1979, 66:239-246.
[2]Gorman D J. Free vibration analysis of rectangular plates with symmetrically distributed point supports along the edges[J]. Journal of Sound and Vibration, 1980, 73:563-574.
[3]Gorman D J. An analytical solution for the free vibration analysis of rectangular plates resting on symmetrically distributed point supports [J]. Journal of Sound and Vibration, 1981, 79:561-574.
[4]Huang M, Ma X Q, Sakiyama T, et al. Free vibration analysis of rectangular plates with variable thickness and point supports [J]. Journal of Sound and Vibration, 2007, 300:435-452
[5]Bapat A V, Suryanarayan S. Free vibrations of rectangular plates with interior point supports [J]. Journal of Sound and Vibration, 1989, 134:291-313.
[6]Narita Y, Hodgkinson J M. Layerwise optimisation for maximising the fundamental frequencies of point-supported rectangular laminated composite plates [J]. Composite Structures, 2005, 69:127-135.
[7]王砚, 王忠民, 阮苗. 无网格法在点弹性支承矩形薄板横向振动中的应用[J]. 计算力学学报. 2010, 27(2):238-243.
WANG Yan, WANG Zhong-min, RUAN Miao.Application of meshless method in the transverse vibration of rectangular thin plate with elastic point supports [J]. Chinese Journal of Computational Mechanics, 2010, 27(2):238-243.
[8]Xu M, Cheng D. A new approach to solving a type of vibration problem [J]. Journal of Sound and Vibration, 1994, 177(4):565-571.
[9]赵凤群, 王忠民. 点弹性支承的非保守矩形薄板的稳定性[J].西安理工大学学报, 1998, 14(4):398-403.
ZHAO Feng-qun, WANG Zhong-min. The stability of non-conservative rectangular plate with spring attachments [J]. Journal of xi’an University of Technology, 1998, 14(4):398-403.
[10]郭强, 沈惠申. 点支撑预应力中厚矩形板的横向振动 [J]. 工程力学,2005, 22(4):106-111.
GUO Qiang, SHEN Hui-shen. Vibrations of initially stressed moderately thick rectangular plates with point supports[J]. Engineering Chanics,2005, 22(4):106-111.
[11]Asku G,Felemban M B.Frequency analysis of corner point supported Mindlin plates by a finite difference energy method[J]. Journal of Sound and Vibration, 1992, 158(3):531-544.
[12]Zhou D, Cheung Y K, Kong J. Free vibration of thick, layered rectangular plates with point supports by finite layer method[J]. International Journal of Solids and Structures, 2000, 37:1483-1499.
[13]Wang C M, Wang Y C, Reddy J N. Problems and remedy for the Ritz method in determining stress resultants of corner supported rectangular plates[J]. Computers and Structures,2002,80: 145-154.
[14]Lopatin A V, Morozov E V. Fundamental frequency of an orthotropic rectangular plate with an internal centre point support[J]. Composite Structures, 2011, 93:2487-2495.
[15]许琪楼. 四角点支承四边自由矩形板自振分析新方法[J].振动与冲击, 2013, 32(3):83-86.
XU Qi-lou.A new analysis method of free vibration of rectangular plate with 4-free-sides and 4-corner point supports[J]. Journal of Vibration and Shock, 2013, 32(3):83-86.

