三轴六自由度电液振动台解耦控制

三轴六自由度电液振动台解耦控制

沈刚1,朱真才1,李翔1,汤裕1,杨寅威1, 丛大成2

(1.中国矿业大学机电工程学院,江苏徐州221116; 2.哈尔滨工业大学机电工程学院,哈尔滨150080)

摘要：为了解决三轴六自由度电液振动台自由度之间耦合问题，提出一种基于逆模型的前馈补偿器解耦策略。对多轴电液振动台的系统传递函数转化为矩阵型式并进行分析，推导出基于系统逆模型解耦控制方案，利用递推增广最小二乘法(Recursive Extended Least Square, RELS)及零相差跟踪技术(Zero Phase Error Tracking，ZPET)设计出系统逆模型并得到相应的解耦控制器。最后，利用六自由度电液振动台对提出的算法进行实验验证。实验结果表明，解耦后的系统性能得到较大改善，一定程度上降低了耦合信号。

关键词：电液振动台;补偿;逆模型;解耦控制;系统辨识

中图分类号:TP271.31

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.001

Abstract:To solve the coupling problem among DOFs of a Triaxial 6-DOF electro-hydraulic shaking table(EHST), a feedforward compensation decoupling strategy was proposed based on an inverse model. Firstly, for the multi-axis electro-hydraulic shaking table, its system transfer function was taken as a form of matrix and analyzed to deduce the decoupling control scheme based on the system inverse model. Then, the system inverse model and corresponding decoupling controller were obtained by employing the recursive extended least square algorithm (RELS) and the zero phase error tracking technology (ZPET). Finaly, tests were conducted on a 6-DOF electro-hydraulic shaking table to verify the validity of the proposed algorithm. The results demonstrated that the proposed decoupling control strategy can greatly improve the system performance.

基金项目：国家自然科学基金项目(11172166)

收稿日期：2014-08-07修改稿收到日期：2014-09-25

Decoupling control for a triaxial 6-DOF Electro-hydraulic shaking table

SHENGang1,ZHUZhen-cai1,LIXiang1,TANGYu1,YANGYin-wei1,CONGDa-cheng2(1. School of Mechanical and Electrical Engineering, China University of Mining and Technology, Xuzhou 221116, China;2. School of Mechanical and Electrical Engineering, Harbin Institute of Technology, Harbin 150080, China)

Key words:electro-hydraulic shaking table; compensation; inverse model; decoupling control; system identification

电液振动台作为振动力学试验中的关键设备[1]，被广泛应用于民用、建筑、汽车和抗震测试等领域[2]，通过模拟被试件在运输及使用过程中所承受的振动环境，确定测试样品是否能够保持正常运行[3]，以及在受到特定的振动和处于振动环境中时是否可以保持结构完整[4]。

振动台伺服系统是保障试验台平稳运行的基本控制系统，首先需要利用参考信号发生器实现加速度控制，然后采用基于极点配置理论的三状态控制拓展液压系统频宽，提高试验台的稳定性[5]; 系统的每个被控制变量应只按其给定值变化，不受或少受其它给定值的影响，并且具备较好的动态和静态性能，即实现解耦控制。

在多自由度液压伺服系统中，耦合作用存在于多通道伺服液压缸同时工作的情况下，一个存在着耦合的系统，由于各回路不能作为独立的研究对象，所以回路参数要进行多次整定，但结果并不理想。因此，耦合问题直接关系到多自由度液压伺服系统的控制效果[7]。对多输入多输出之间相互有关联的控制系统，实现每个输出只受一个输入控制，而且不同输出各受不同的输入所控制，这就是解耦问题。

为解决多自由度液压伺服系统存在的耦合问题，国内外学者提出了一些解耦控制策略。王庆丰等[8]采用对角矩阵法，对比例双阀控液压缸位置耦合控制系统进行了解耦设计，并在系统实验装置中得到了实现。张永杲等[9]提出了一种基于广义最小方差预测校正的参考模型自适应解耦控制，避开了研究系统非线性环节的模型。王洪瑞等[10]提出将耦合项等效为外干扰，设计具有积分补偿的动态全阶滑模变结构控制器，实现了解耦和对外干扰及参数摄动的不变性。

本文针对三轴六自由度电液振动台系统存在的耦合问题，采用前馈补偿器解耦方法对三轴液压振动台进行解耦控制，综合运用系统辨识、零相差跟踪等理论，首先研究振动台存在的耦合问题，将系统传递函数转化为并矩阵进行分析，提出解耦方案，然后运用递推增广最小二乘法辨识振动台加速度闭环系统的传递函数模型，运用零相差跟踪技术设计非最小相位系统的稳定逆模型，得到解耦控制器，最后利用搭建的电液振动台对提出的解耦控制策略进行试验验证。

1试验方案

图1是用于实验验证的6自由度电液振动台，主要由平台、伺服阀、液压缸、液压源以及连接球铰等组成。每支液压缸上安装有线性可变差动变压器(LVDT)和压差传感器，实时反馈液压缸位移和上下腔压力差；加速度传感器安装在振动台上。试验台相关技术指标如表1所示。图2为电液振动台系统组成框图，图3是电液振动台的控制系统原理图。6自由度加速度指令信号经控制算法产生期望的6自由度位移信号，经自由度分解矩阵转化为8个激振器的驱动信号并与振动台的位移输出构成位置闭环，加速度反馈信号用于提高系统的稳定性，经控制器调节后产生±10V的驱动信号并由D/A板卡PCL-6126采集，生成的驱动信号再经过信号调理电路和功率放大器产生±40mA的电流信号以驱动电液伺服阀，振动台将按照期望的信号进行运动。位移、加速度和压差反馈信号由A/D板卡PCL-816进行采集。实验系统由基于MATLAB/Simulink快速原型的xPC内核实时系统进行控制，提出的控制算法在MATLAB/Simulink中编写完成后由Microsoft Visual Studio.NET进行编译，之后下载到xPC内核中实现，试验系统的采样时间为1ms。

图1　实验电液振动台 Fig.1 Experimental system of the EHST

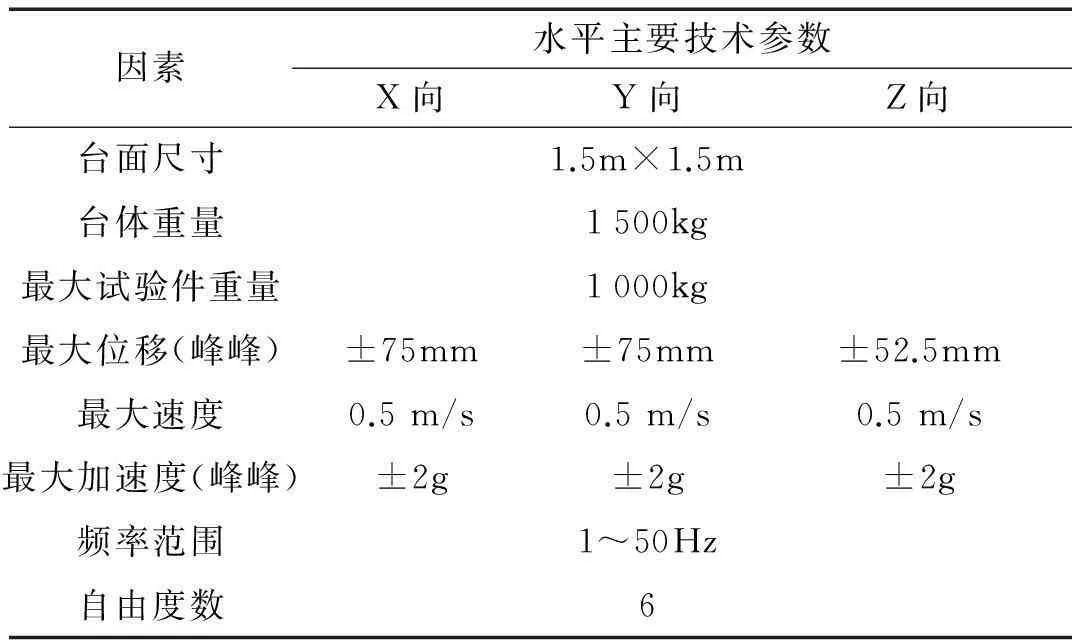
因素水平主要技术参数X向Y向Z向台面尺寸1.5m×1.5m台体重量1500kg最大试验件重量1000kg最大位移(峰峰)±75mm±75mm±52.5mm最大速度0.5m/s0.5m/s0.5m/s最大加速度(峰峰)±2g±2g±2g频率范围1～50Hz自由度数6

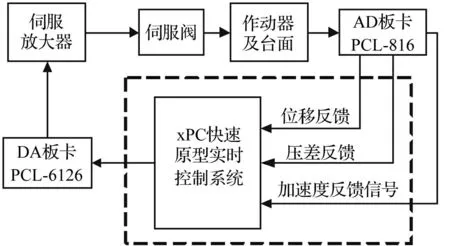
图2　电液振动台试验系统的组成 Fig.2 Structure of EHST experiment system

图3　电液振动台伺服控制系统结构 Fig.3 Structure of EHST servo control system

2提出的解耦控制器

本文仅考虑三轴六自由度振动台的垂直向解耦问题，即具有Z自由度、Rx和Ry自由度之间存在的耦合问题。Y自由度、Rx和Rz自由度之间以及X自由度、Ry和Rz自由度之间耦合问题解决方案与垂直解耦相同。

图3是垂直向三个自由度之间的耦合情况。每个自由度的参考信号不仅对自身自由度有一个输出响应而且对另外两个自由度也造成了输出响应，所以三个自由度有9个输出，yRyz (k),yzz(k),yRxz (k),yZRx(k),yRxRx(k),yZRy(k),yRyRy(k),yRxRy(k),yRyRx(k)，这使得各自由度之间存在相互影响，不能分开单独考虑。

图4　振动台Z方向三自由度之间的耦合 Fig.4　3 DOF MIMO decouple control stratehy based on transfer function

设三自由度液压振动台的传递函数矩阵具有下面的形式

(1)

式中:GZZ(z),GZRx(z)…GRyRy(z)为各自由度之间的传递函数。

系统的输出和输入可写成如下关系

(2)

可见，每个输入uZ，uRx，uRy和3个输出存在相互关联；每个输出yZ，yRx，yRy受3个输入的控制，每个量都相互制约，相互交联。

若能使液压振动台的三自由度传递函数矩阵变成如下的非奇异对角型：

(3)

那么称这样的系统是解耦的。

本文采用前馈补偿器解耦方法对三轴液压振动台进行解耦控制，需要在待解耦的系统前面串接一个前馈补偿器使串联组合系统的传递函数阵成为对角形的有理函数矩阵。

设液压振动台的三自由度输入和输出有下列关系表达：

(4)

式中:GZZ(z)，GRxRx(z)和GRyRy(z)为三自由度的加速度传递函数；kZZ,kZRx…kRyRy为各个自由度的随机耦合增益(非对角线有非零元素值)。

为了达到解耦的目的，则有下面的关系：

(5)

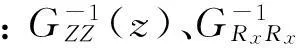
为使上式的三自由度液压振动台的传递函数矩阵变成非奇异对角型，则有：

(6)

设前馈补偿器为GcZ(s)、GcRx(s)和GcRy(s)，则补偿后的表达式为：

(7)

式中：

(8)

根据公式(7)，可以得到三自由度振动台的解耦原理，如图5所示。

图5　Z方向三自由度解耦原理 Fig.5 Decouple of 3DOF for Z-axis

同理，对于x，y方向，分别设前馈补偿器为GcX(s)、GcRy(s)、GcRZ(s)和GcY(s)、GcRX(s)、GcRZ(s)，则补偿后的表达式分别为：

(9)

(10)

式中:

(11)

(12)

根据公式(9)和(10)，可以分别得到X和Y方向的三自由度解耦原理，如图6、7所示。

图6　y方向三自由度解耦原理 Fig.6 Decouple of 3DOF for y-axis

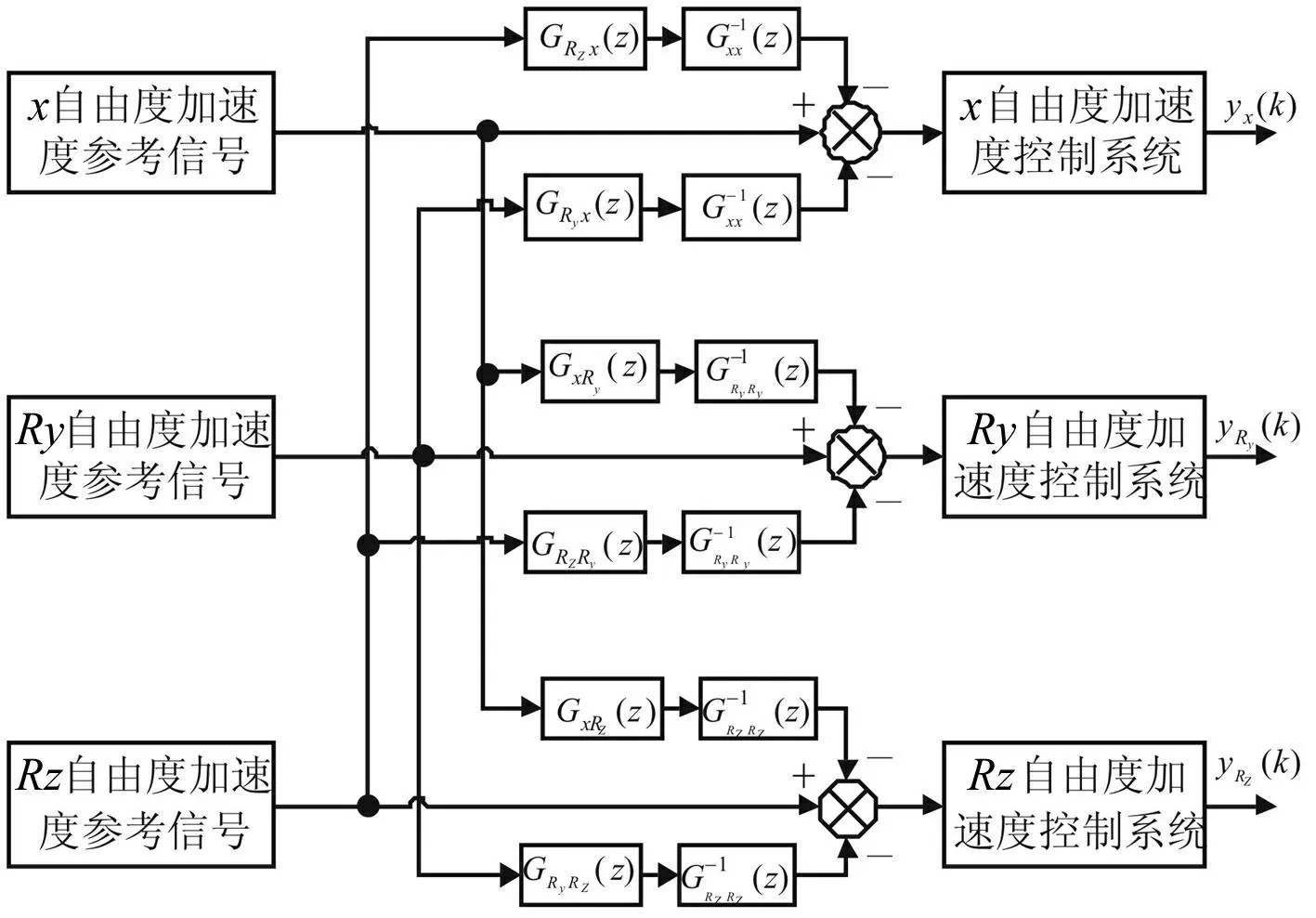
图7　x方向三自由度解耦原理 Fig.7 Decouple of 3DOF for x-axis

3系统辨识及逆模型设计

本文采用递推增广最小二乘法(Recursive Extended Least Square, RELS)辨识振动台加速度闭环系统的传递函数模型。RELS的估计公式为[11]

(13)

(14)

(15)

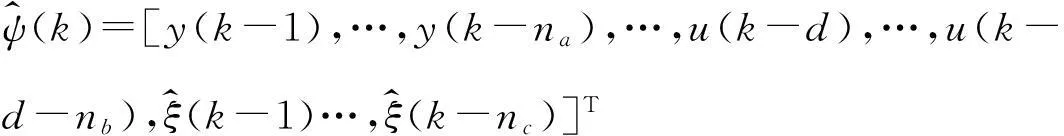
(16)

将公式(16)分解成为

(17)

在辨识模型的基础上，利用零相差跟踪(ZPET)控制技术得到识振动台加速度闭环系统的传递函数的逆模型，该技术通过在前馈控制器中引入零点来补偿闭环系统的不稳定零点。

闭环系统的逆传递函数可设计为[12]：

(18)

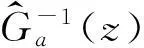
补偿系统可表示为

Gc(s)=eLTs=

(19)

逆传递函数为：

(20)

式中:Gc(z)为Gc(s)的z变换。

4实验结果

本文利用图1所示电液振动台进行试验，对提出的解耦控制算法进行验证，文中试验结果均为空载状态下得到。由于三自由度加速度解耦控制部分需要辨识出非对角线的传递函数以及主对角线的逆传递函数，采用2～100Hz的加速度随机信号激励基于三状态控制器的加速度闭环系统。利用参考信号激励Z自由度系统同时可以获得Z自由度的加速度输出响应以及另外两个自由度的耦合信号，同理可以获得另外6路加速度反馈信号，将采集的3路加速度参考信号和9路振动台加速度输响应并输出到RELS辨识程序中，即可得到9个传递函数。

限于篇幅，本文仅给出Z自由度辨识结果及逆传递函数设计过程。采用RELS算法离线辨识出Z自由度加速度闭环系统的传递函数如下：

(21)

由公式(18)设计出Z自由度加速度闭环逆传递函数为：

(22)

图8　Z自由度加速度实验模型与设计逆模型 Fig.8 Identification results of experimental and designed inverse model of Z DOF acceleration

Z自由度加速度实验模型与设计逆模型如图8所示，RELS辨识出9个传递函数的幅频特性如图9所示，实线是辨识出的模型，虚线是振动台的实际响应。对于模型的辨识精度，通过使用公式(19)计算辨识模型与试验结果传递函数幅频特性幅值的误差进行衡量：

(23)

式中:ya(k)为辨识模型传递函数幅频特性幅值；ra(k)为试验结果传递函数幅频特性幅值。

根据公式(23)，可得各自由度之间的模型偏差见表2。

通过以上数据可以看出，模型的辨识误差在0.25以内，具有较高的辨识精度。

表2　辨识模型与试验结果传递函数辨识误差

根据解耦补偿公式(7)，从该式中看到：进行解耦之前需要得到3自由度的非对角线元素的传递函数以及主对角线的逆传递函数。通过实验辨识出三自由度振动台加速度系统的9个传递函数并离线设计出3个主对角线的加速度逆传递函数，根据公式(7)的解耦原理对3自由度加速度闭环系统进行解耦控制。通过图10所示解耦前后的非对角线元素的幅频特性对比，可以看出解耦后的系统性能得到较大改善，一定程度上降低了耦合信号。

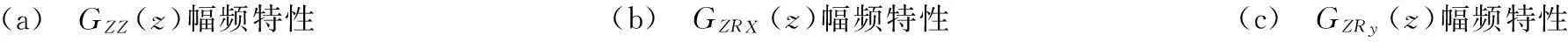
(a) GZZ(z)幅频特性(b) GZRX(z)幅频特性(c) GZRy(z)幅频特性

(d) GRXZ(z)幅频特性(e) GRXRX(z)幅频特性(f) GRXRy(z)幅频特性

(g) GRyZ(z)幅频特性(h) GRyRy(z)幅频特性(i) GRyRX(z)幅频特性图9 基于RELS辨识结果Fig.9TheexperimentalidentificationresultswithRELS

(a) GZRX(z)幅频特性(b) GZRy(z)幅频特性(c) GRXZ(z)幅频特性

(d) GRXRy(z)幅频特性(e) GRyZ(z)幅频特性(f) GRyRX(z)幅频特性图10 解耦前后的幅频特性Fig.10Magnitudecharacteristicwithandwithoutdecouple

为了进一步看出解耦的效果，图11给出了Z自由度40Hz正弦信号在解耦前后时域波形复现的效果，图12给出了Z自由度2～40Hz随机信号在解耦前后时域波形复现的效果。从这两组实验结果可以看到解耦后的正弦加速度耦合信号从0.1g 降到0.03g，随机加速度耦合信号从0.05g 降到0.01g，达到了实验要求，实验结果表明了解耦控制策略的有效性。

图11　Z自由度正弦解耦实验结果 Fig.11 Decouple experimental results of Z DOF with 40Hz sine

图12　Z自由度随机信号解耦结果 Fig.12 Decouple experimental results of Z DOF

5结论

(1) 对于系统存在的耦合问题，可以将系统传递函数转化为矩阵的形式进行分析，使系统各自由度之间的关系明显，方便进行解耦控制策略的研究。

(2) 提出一种基于逆模型前馈补偿器解耦方法，通过实验结果中对解耦前后非对角线元素的幅频特性以及加速度耦合信号的对比，表明了解耦控制策略的有效性。

参考文献

[1]沈刚.三自由度电液振动台时域波形复现控制策略研究[D].哈尔滨：哈尔滨工业大学, 2011.

[2]于慧君. 电液振动试验系统长时间历程复现控制技术研究[D]. 杭州：浙江大学, 2009.

[3]杨志东.液压振动台振动环境模拟的控制技术研究[D]. 哈尔滨：哈尔滨工业大学, 2009.

[4]Severn R T.The development of shaking tables-a historical note[J]. Earthquake Engineering & Structural Dynamics, 2011, 41(2):195-213.

[5]Tagawa Y, Kajiwara K. Controller development for the E-Defense shaking table [J]. Proc.IMechE Part I: J. Systems and Control Engineering, 2007, 221(2): 171-181.

[6]韩俊伟.大型地震模拟振动台的研制[D].哈尔滨：哈尔滨工业大学,1996.

[7]杨勇.多自由度液压伺服系统的控制策略研究[D].长沙：中南大学,2008.

[8]王庆丰，路甬祥．电液多变量位置系统的解耦控制[J]．中国机械工程,1998,11(7):729-732．

WANG Qing-feng, LU Yong-xiang. Decoupling control of electro-hydraulic multivariable position control system[J]. China Mechanical Engineering,1998,11(7):729-732．

[9]张永杲，张志洪，熊宇飞．非线性多变量电液伺服系统解耦自适应控制[J]．上海交通大学学报, 1994, 28(2): 23-30．

ZHANG Yong-gao, ZHANG Zhi-hong, XIONG Yu-fei. Adaptive decoupling control of nonlinear multivariable electrohydraulic servo system[J]. Journal of Shanghai Jiaotong University, 1994, 28(2): 23-30．

[10]王洪瑞，方一鸣，焦晓红．状态反馈鲁棒解耦控制器的设计[J]．控制与决策,1994,9(4):306-310．

WANG Hong-rui, FANG Yi-ming, JIAO Xiao-hong. The design for decoupling robust controller with the state feedback[J]. Control and Decision, 1994,9(4):306-310．

[11]Cowan C F N, Grant P M. Adaptive filters[M]. Prentice-Hall, Inc., Englewood Cliffs, New Jersey. 1985.

[12]Shen Gang, Zhu Zhen-cai, Han Jun-wei. Adaptive feed-forward compensation for hybrid control with acceleration time waveform replication on electro-hydraulic shaking table[J]. Control Engineering Practice,2013, 21(8): 1128-1142.

第一作者王剑男，博士生，1988年5月生