基于矩阵秩最小化和统计修正的信号降噪方法研究

基于矩阵秩最小化和统计修正的信号降噪方法研究

李文峰1,2，许爱强1，戴豪民1，王丰3

(1.海军航空工程学院科研部,山东烟台264001；2.92635部队山东青岛266041； 3.海军航空工程学院91206部队,山东青岛266108)

摘要：针对奇异值分解在信号降噪时有效秩的选择问题，提出一种基于矩阵秩最小化和统计修正的信号降噪方法。首先，利用矩阵秩最小化理论将奇异值有效秩选择问题转化为秩的约束优化问题；然后，通过凸优化求解，得到干净信号的Hankel矩阵，实现一次降噪；最后，根据奇异值子集标准差对干净信号Hankel矩阵进行统计修正，进一步优化降噪效果。模拟信号和真实信号的实验结果表明：该方法可以有效的消除脉冲干扰和高斯噪声，能够最大限度的降低信号均方误差，提高信噪比，增强了奇异值分解在信号降噪中的通用性。

关键词：奇异值分解；奇异值扰动理论；矩阵秩最小化；奇异值子集标准差

中图分类号:TN911.7文献标志码：A

Signal denoising method based on matrix rank minimization and statistical modification

LIWen-feng1,2,XUAi-qiang1,DAIHao-min1,WANGFeng3(1. Research Department, Naval Aeronautical and Astronautical University, Yantai 264001, China;2. No. 92635 Unit of PLA,Qingdao 266041, China；3. No. 91206 Unit of PLA, Naval Aeronautical and Astronautical University, Qingdao 266108, China)

Abstract:Aiming at the selection problem of effective ranks in singular value decomposition for signal denoising, a signal denoising method based on matrix rank minimization and statistical modification was proposed. Firstly, the effective rank selection problem of singular value decomposition was transformed into a constrained optimization problem of rank by using the matrix rank minimization theory. Secondly, Hankel matrix of a clean signal was obtained with a convex optimization to realize the first noise reduction. At last, the statistical correction was performed for the clean signal’s Hankel matrix with subset standard deviation of a singular value to further optimize the noise reduction effect. The simulated signal and real signal test results showed that the method can effectively eliminate pulse noise and Gaussian noise; at the same time, the method can reduce the maximum signal mean square error and improve the signal-to-noise ratio; so the method can enhance the universality of singular value decomposition in signal denoising.

Key words:singular value decomposition (SVD); matrix perturbation theory; matrix rank minimization; subset standard deviation of singular value

信号在产生、采集和传递时往往伴有噪声的干扰，因此信号预处理中的信号降噪是保证后续信号分析的重要前提。传统的降噪方法如小波降噪和基于谱分析的滤波方法，其原理是利用信号与噪声的频谱不同达到降噪的效果。但是，当有用信号和噪声频带混叠严重时，传统的降噪方法则具有较大的局限性。近年来，奇异值分解(Singular Value Decomposition，SVD)在信号降噪问题上已经得到了广泛应用，其中奇异值有效秩选择问题一直是当前研究的热点和难点。Donoho等[1]提出了奇异值优化硬阈值法，给出了硬阈值的优化选择标准；赵学智等[2]提出了奇异值差分谱法，根据差分谱峰值位置可实现对有用分量个数的确定，王建国等[3]在奇异值差分谱的基础上提出单边极大值选择方法，即在奇异值差分谱中从右至左，选择第一个至少单边与其相邻峰值比较，差距绝对值最大的极大峰值的对应点位置，来确定重构信号的有效秩阶次，钱征文等[4]采用信号快速傅里叶变换结果中主频个数来确定奇异值数目,王树青等[5]采用奇异值相对变化率确定信号降噪时奇异值的有效秩。

以上方法在高斯噪声的背景下均取得了较好的降噪效果。但是也存在两个问题：一是噪声中如果包含稀疏大噪声，比如脉冲信号，则上述方法效果欠佳；二是在奇异值个数选择上，均是一次性截断奇异值，容易造成了奇异值有效秩选择的武断性。针对上述问题，本文首先从矩阵奇异值扰动理论角度分析截断奇异值方法的局限性；其次，利用矩阵秩最小化理论将有效秩选择问题转化为秩的约束优化问题，并通过凸优化求解得到干净信号的Hankel矩阵。最后根据奇异值子集标准差对干净信号Hankel矩阵进行统计修正，进一步优化降噪效果。实验结果表明：相比于其他方法，该算法可以消除混合噪声对信号的影响，增强了SVD在信号降噪中的可用性和有效性。

1奇异值分解降噪原理

(1)

式中，K=N-L+1，表示矩阵的嵌入维数，L是滑动窗口长度。矩阵Z是一个Hankel矩阵，即矩阵反对角线上元素相等。对矩阵Z进行奇异值分解，得：

(2)

式中，ui和vi分别是Z的左右奇异向量，d表示矩阵Z的秩，即非零奇异值个数，且d≤min(L,K)，λ1,λ2,…,λd是按降序排列的Z的奇异值。SVD降噪的本质就是通过选择合适奇异值的个数，实现干净信号矩阵X和噪声矩阵E的分离，即Z=X+E。最后，对分离出的干净信号矩阵X进行对角平均化，即可将该矩阵重构为长度为N的一维序列，重构序列的计算公式如下：

(3)

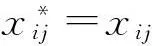
在利用SVD进行信号降噪时有两个问题需要考虑，一是构造轨迹矩阵时的窗口长度L的选择问题。文献[6]从重构序列各成分的分离性和重构误差的角度上推荐L取序列长度N的中值(如果N为偶数，取L=N/2)；文献[7]研究了轨迹矩阵的奇异值随窗口长度L的变化规律，从理论上证明了当L取N的中值时，对应的奇异值会取得最大值，同时该文献也推荐在大多数情况下L取N的中值是最佳的选择。二是分离干净信号矩阵所需的奇异值个数，即有效秩的选择问题。传统方法大多从奇异值分布曲线的变化突点，即曲线“肘部”处截断奇异值来确定干净信号矩阵的秩，此类方法操作简单，但是对脉冲噪声或脉冲和高斯混合噪声就会失效，接下来从矩阵奇异值扰动理论来说明截断奇异值方法的失效原因。

2矩阵奇异值扰动理论

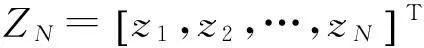
(4)

(5)

(6)

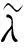
(7)

从式(7)中可以看出，在高信噪比的情况下，通过选择前r个较大的奇异值逼近干净信号矩阵是合理的。但是在低信噪比情况下或者信号受到稀疏大噪声污染，虽然通过一次性截断奇异值能够移除部分噪声，仍会有部分噪声对前r个奇异值产生扰动，所以重构信号也将产生较大误差。

3基于矩阵秩最小化的降噪方法

3.1矩阵秩最小化理论

Wright等[9]提出了鲁棒主成分分析(Robust Principal Component Analysis，RPCA)算法，证明了通过解优化问题能够从被污染矩阵中精确恢复出所需的低秩矩阵。因此，将奇异值有效秩选择问题转化为矩阵秩的约束优化问题，可以客观地解决奇异值有效秩选择问题。

当数据矩阵具有低秩性的结构[10-11]，并且只有少部分元素被噪声严重污染，即噪声是稀疏的，那么矩阵降噪问题可用如下模型来描述：

minrank(S)+γ‖W‖0

s.t.S+W=Z

(8)

min‖S‖*+γ‖W‖1

s.t.S+W=Z

(9)

这样就将求解矩阵秩的非凸问题转化为凸优化问题，使得该问题具有唯一解。

更为一般的情况，假定低秩矩阵S既被轻微高斯噪声E所污染，也被稀疏大噪声W所污染，并且E中元素满足Ei,j～N(0,σ2)，‖E‖F≤δ，δ>0，那么矩阵降噪就可以用如下优化问题来描述[13]：

min‖S‖*+γ‖W‖1

s.t.‖Z-S-W‖F≤δ

(10)

目前，求解式(9)和式(10)最优化问题有多种算法，最为常用的是非精确增广拉格朗日乘子法(Inexact Augmented Lagrange Multiplier，IALM)，算法的详细描述及收敛性证明参见文献[14]。

3.2仿真实验

综合上述分析，为去除信号中的噪声干扰，将秩最小化理论应用于SVD中实现降噪的步骤如下：

(1)通过嵌入操作，将长度N的含噪序列ZN=[z1,z2,…,zN]T映射为轨迹矩阵Z∈RL×K，K=N-L+1，L=N/2。

(2)根据式(9)或式(10)，利用IALM算法恢复出低秩矩阵S。

(3)将低秩矩阵S对角平均化，转化成所需的长度为N的干净信号序列，最终实现信噪分离。

为了验证降噪效果，采用信号均方误差(Mean Square Error，MSE)和信噪比(Signal to Noise Ratio，SNR)来评价各种方法的优劣，其定义形式如下：

(11)

(12)

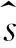
实验1 考察以下仿真信号：

z(t)=s(t)+w(t)=

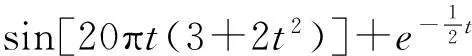
式中，w(t)是随机添加的21个脉冲噪声。

图1　三种方法降噪效果 Fig.1 Denoising effect of three methods

文献[1-5]采用的噪声实例均是高斯噪声，笔者经仿真实验发现这些方法不能有效地去除脉冲噪声。由于中值滤波(Median Filter，MF)具有抑制脉冲干扰的作用，所以采用中值滤波以及常见的小波阈值降噪与本文方法对比。各种方法的降噪效果如图1所示。

表1　三种方法降噪后的信号MSE和SNR

从图1可以看出，小波阈值降噪方法无法消除脉冲噪声，中值滤波方法可以较好的抑制脉冲干扰，但是中值滤波受窗口长度的影响，抑制脉冲干扰效果并不稳定，过长的窗口长度容易使信号更加平滑，误差较大，过短的窗口长度则不能有效抑制过于“密集”的脉冲干扰(如图1a放大窗口所示)。相比较前两种方法，本文方法在抑制脉冲干扰时效果最佳。表1是各种方法降噪后的MES和SNR，从表1也可以看出，基于矩阵秩最小化的SVD降噪方法表现特别优秀，几乎完全恢复干净信号，其误差精度可以忽略不计。

实验2考察以下仿真信号：

x(t)=s(t)+e(t)+w(t)=

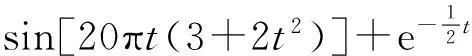
式中，e(t)为信噪比是5 dB的高斯白噪声，w(t)是随机添加的17个脉冲噪声。首先采用中值滤波方法滤除仿真信号的脉冲干扰，然后结合文献[1,3-5]方法与矩阵秩最小化方法对剩余混合噪声进行降噪效果对比。

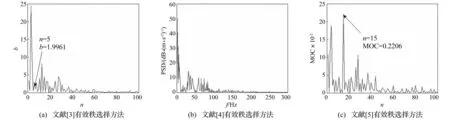
图2　文献[3]、[4]和[5]的有效秩选择方法 Fig.2 Effective rank selection method of literature [3],[4] and [5]

文献[1]提出的奇异值优化硬阈值方法，通过计算优化硬阈值为24.669 6；文献[3]提出的奇异值差分谱单边极大值方法，从图2(a)中计算得到所需的奇异值有效秩为5；文献[4]提出用于恢复有用信号的奇异值个数等于信号功率谱主频个数的两倍，由于图2(b)中功率谱主频个数并不清晰可见，所以近似选择奇异值有效秩为10；文献[5]提出的奇异值相对变化率方法，从图2(c)中得到所需的奇异值有效秩为15。

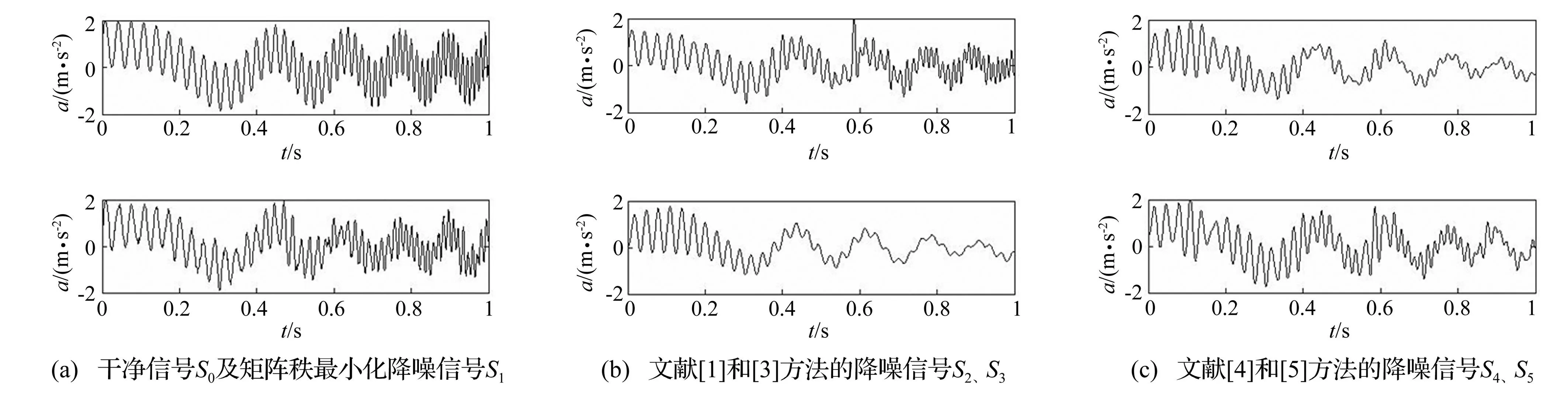
图3　五种方法降噪效果 Fig.3 Denoising effect of five methods

从图4和表2可以看出，在高斯噪声和脉冲噪声组成的混合噪声背景下，矩阵秩最小化方法降噪效果优于其他四种降噪方法，可以完全滤除脉冲信号的干扰，但是由于高斯噪声的影响，恢复出的信号与原始信号相比，还存在部分失真。针对上述问题，接下来采用奇异值子集标准差方法对矩阵秩最小化降噪后的信号进行统计修正，进一步优化降噪效果。

4基于奇异值子集标准差的统计修正降噪

4.1奇异值子集标准差统计修正方法

矩阵秩最小化降噪方法虽然可以滤除大部分混合噪声，但仍存在部分高斯噪声造成恢复出的信号失真。需要注意的是，此时恢复出的信号具有高信噪比的特点，因此可以根据奇异值分布曲线的“肘部”来选择奇异值的个数。为了能够更加清晰的观察奇异值“肘部”处的变化情况，本文采用文献[15]提出的奇异值子集标准差方法来确定奇异值个数，实现二次降噪，具体步骤如下：

(1)对秩最小化恢复出的干净信号矩阵进行奇异值分解；

(2)将得到的奇异值按升序排列，即τ1≤τ2≤...≤τn；

(3)构建奇异值子集Γ1={τ1},Γ2={τ1,τ2},…,Γn={τ1,τ2,…,τn}；

(4)计算每个子集的标准差{σ1,σ2,…,σn}，并向下取整，即iσi=⎣σi,i=1,2,…,n，若kσk≠0，则计算终止。存储从第k个一直到最后一个奇异值，然后将存储的n-k+1个奇异值进行信号重构，得到最终的干净信号。

采用奇异值子集标准差进行统计修正的详细流程见图4。

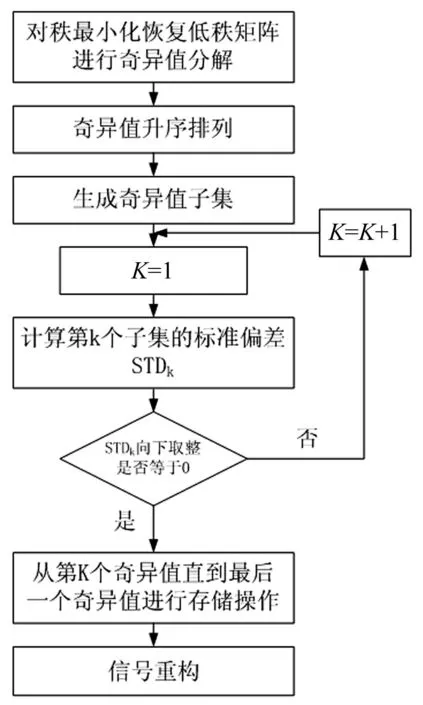
图4　奇异值子集标准差统计修正方法流程 Fig.4 The process based on subset standard deviation of the singular value for statistical correction

4.2仿真分析

图5是采用子集标准差方法对矩阵秩最小化方法恢复出的信号进行统计修正后的奇异值分布曲线。从图5可以清晰的看出奇异值“肘部”的变化情况，从第467个奇异值一直到最后一个奇异值，其标准差均不为0，所以选择467到512个奇异值进行信号重构。从图6的重构信号可以看出，信号的失真程度已经变小。从表2也可以看出，在对混合噪声进行降噪时，基于矩阵秩最小化结合统计修正的信号降噪方法要明显优于其他四种降噪方法。

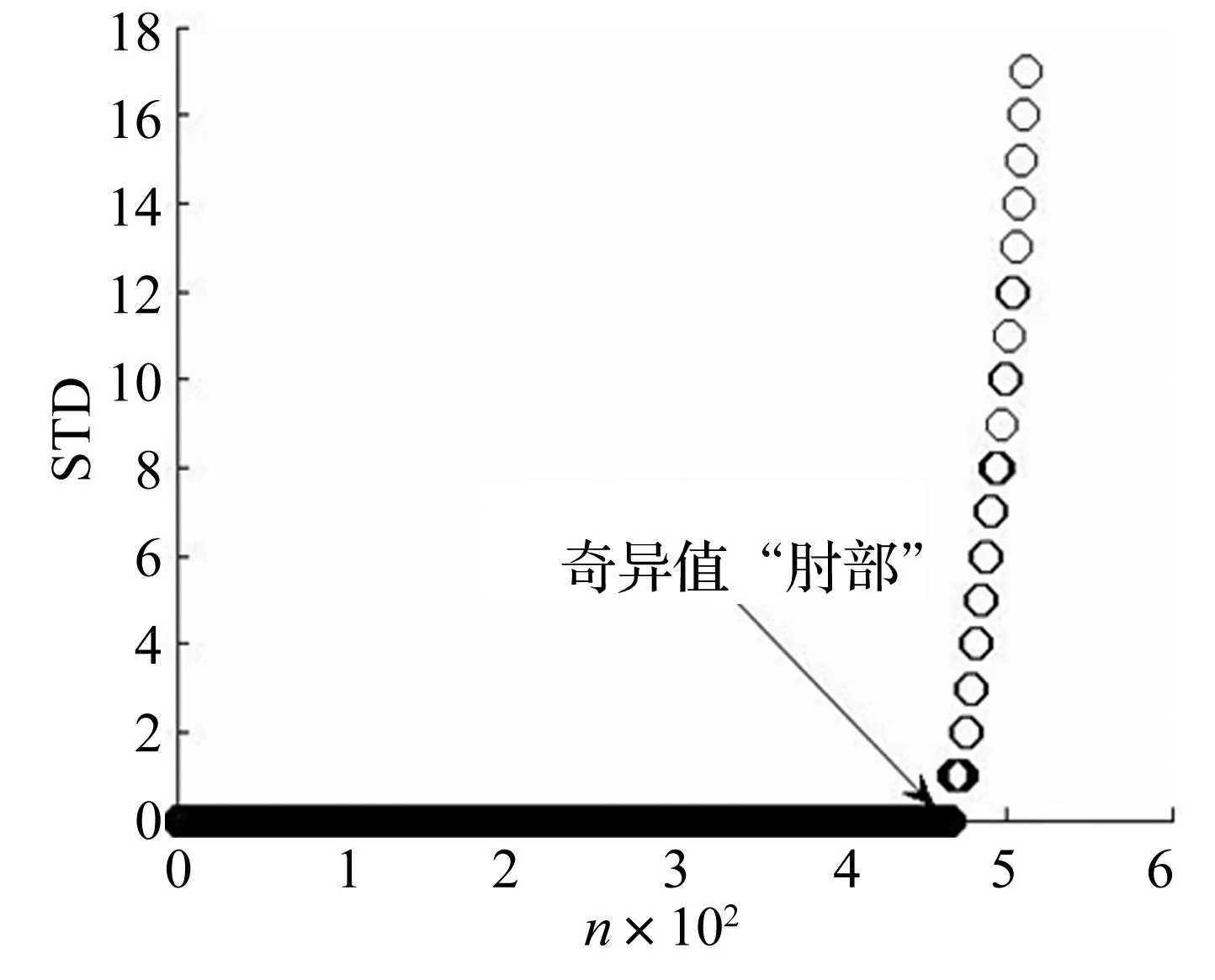
图5　奇异值子集标准差选择奇异值有效秩 Fig.5 The selection problem of effective rank

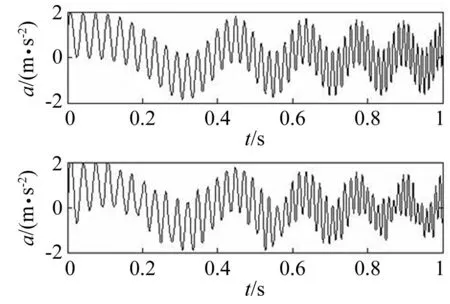
图6　干净信号S 0及矩阵秩最小化 和统计修正降噪信号S 6 Fig.6 The clean signal S 0 and statistical correction denoising signal S 6

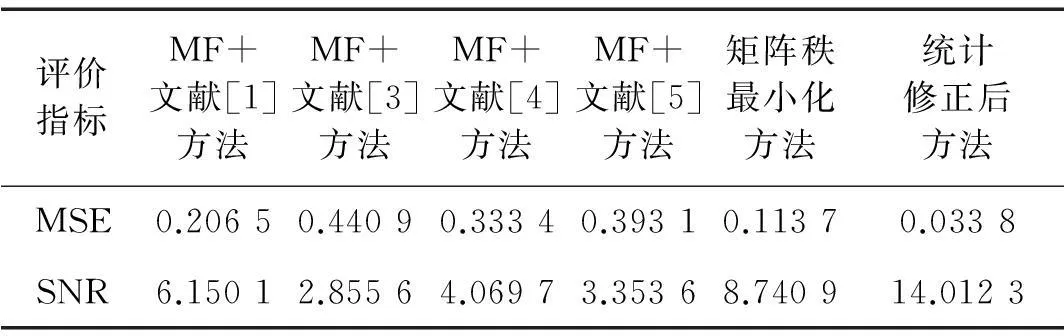
评价指标MF+文献[1]方法MF+文献[3]方法MF+文献[4]方法MF+文献[5]方法矩阵秩最小化方法统计修正后方法MSE0.20650.44090.33340.39310.11370.0338SNR6.15012.85564.06973.35368.740914.0123

5实例分析

图7a为电机轴承正常状态下的振动加速度信号，信号中含有脉冲干扰。当电机轴承正常运行时，其振动信号应是平稳的随机波形，所以可以认为图中的尖峰是由异常运行情况导致，如果不消除这些脉冲干扰，将会对后续的信号分析及轴承故障诊断时的状态分类产生较大影响。此外，本文提出的信号降噪方法同时也适用于解决图像分析与处理、计算机视觉等其他领域。采用本文提出的基于矩阵秩最小化和统计修正方法对振动信号进行降噪后的信号如图8(a)所示。图7(b)、(c)和图8(b)、(c)分别是对实测信号和降噪后信号进行经验模态分解(Empirical Mode Decomposition，EMD)后得到的固有模态函数(Intrinsic Mode Function，IMF)，从图中可以看出，原实测信号经EMD分解后产生11个imf分量和1个残余分量，各模态之间产生混叠现象，而降噪后信号经EMD分解产生7个imf分量和1个残余分量，能够较好反映真实信号的成分。

图7　电机轴承实测信号及其imf分量 Fig.7 The vibration signal of motor bearing and its imf components

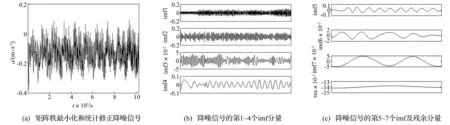
图8　本文方法降噪信号及其imf分量 Fig.8 The denoising signal by this paper method and its imf components

6结论

(1)从矩阵奇异值扰动理论角度分析了传统奇异值分解方法在信号降噪时的局限性，提出利用矩阵秩最小化理论将奇异值有效秩选择问题转化为秩的约束优化问题，并通过凸优化求解，实现一次降噪。

(2)提出利用奇异值子集标准差方法将矩阵秩最小化恢复出的干净信号矩阵进行统计修正，实现二次降噪。

(3)通过模拟信号和实测振动信号进行降噪仿真分析，验证了本文方法的有效性，增强了奇异值分解在信号降噪中通用性。

参考文献

[2]赵学智,叶彦邦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报, 2010, 46(1):100-108.

ZHAO Xue-zhi, YE Yan-bang, CHEN Tong-jian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe [J]. Journal of Mechanical Engineering, 2010, 46(1):100-108.

[3]王建国,李健,刘颖源.一种确定奇异值分解降噪有效秩阶次的改进方法[J]. 振动与冲击, 2014, 33(12):176-180.

WANG Jian-guo, LI Jian, LIU Yian-yuan. Animproved method for determining effective order rank of SVD denoising [J]. Journal of Vibration and Shock, 2014, 33(12):176-180.

[4]钱征文,程礼,李应红.利用奇异值分解的信号降噪方法[J].振动,测试与诊断,2011, 31(4): 459-463.

QIAN Zhen-wen, CHENG Li, LI Ying-hong. Signal denoising method by means of SVD[J]. Journal of Vibration Measurement & Diagnosis, 2011, 31(4):459-463.

[5]王树青,林裕裕,孟元栋,等. 一种基于奇异值分解技术的模型定阶方法[J]. 振动与冲击, 2012,31(15):87-91.

WANG Shu-qing, LIN Yu-yu, MENG Yuan-dong, et al. Model order determination based on singular valued decomposition[J]. Journal of Vibration and Shock, 2012,31(15):87-91.

[6]Golyandina N. On the choice of parameters in singular spectrum analysis and related subspace-based methods [DB/OL]. (2010-07-20).http://arxiv.org/abs/1005.4374vl.

[7]Mahmoudvand R, Zokaei M. On the singular values of the Hankel matrix with application in singular spectrum analysis[J]. Chilean Journal of Statistics, 2012, 3(1): 43-56.

[8]Hassani H, Xu Z Y, Zhigljavsky A. Singular spectrum analysis based on the perturbation theory[J]. Nonlinear Analysis : Real World Applications,2011,12:2752-2766.

[9]Wright J, Ganesh A, Rao S, et al. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization[C]//The Twenty-Fourth Annual Conference on Neural Information Processing Systems, Vancouver, 2009: 2080-2088.

[10]Candès E J, Tao T. The power of convex relaxation: Near-optimal matrix completion[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2053-2080.

[11]Candes E J, Plan Y. Matrix completion with noise[J]. Proceedings of the IEEE, 2010, 98(6): 925-936.

[12]彭义刚,索津莉,戴琼海,等.从压缩传感到低秩矩阵恢复: 理论与应用[J].自动化学报, 2013, 39(7): 981-994.

PENG Yi-gang, SUO Jin-li, DAI Qiong-hai, et al. From compressed sensing to low-rank matrix recovery: theory and applications[J]. Acta Automatica Sinica, 2013, 39(7): 981-994.

[13]Zhou Z, Li X, Wright J, et al. Stable principal component pursuit[C]//Proceedings of the IEEE International Symposium on Information Theory. Austin, IEEE, 2010: 1518-1522.

[14]Lin Z, Chen M, Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[DB/OL].(2010-09-26).http://arxiv.org/abs/1009.5055v3.

[15]Ashtiani M B, Shahrtash S M. Partial discharge de-noising employing adaptive singular value decomposition[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(2): 775-782.