基于正交匹配追踪的强脉冲电磁干扰滤波新方法

基于正交匹配追踪的强脉冲电磁干扰滤波新方法

朱会杰， 王新晴，芮挺,赵洋， 李艳峰

(解放军理工大学野战工程学院，南京210007)

摘要：针对强脉冲电磁干扰能量大、规律性不强，对信号污染严重，提出了一种滤波新方法。依据信号和脉冲电磁干扰结构的不同，构造了单位脉冲原子匹配脉冲电磁干扰，选择正弦原子、余弦原子和小波原子匹配有用信号。不同于常规稀疏分解滤波的思路，本文首先将脉冲电磁干扰看作信号成分，使用上述原子利用正交匹配追踪进行分解。然后，仅选择正弦原子、余弦原子和小波原子匹配的成分作为无噪信号，并将单位脉冲原子匹配的成分作为干扰滤除。仿真实验和实例应用证明，该方法能够有效抑制强脉冲电磁干扰和白噪声，不仅信噪比高，而且保留了细节。

关键词：正交匹配追踪；滤波；脉冲电磁干扰；多原子

中图分类号:TN911.4文献标志码：A

A new denoising method for strong pulse electromagnetic interference signals based on orthogonal matching pursuit

ZHUHui-jie,WANGXin-qing,RUITing,ZHAOYang,LIYan-feng(College of Field Engineering, PLA University of Science and Technology, Nanjing 210007, China)

Abstract:Because strong pulse electromagnetic interferences (PEMIs) have a high energy and a weak regularity, and they pollute signals seriously, a new denoising method to solve this problem was proposed. According to different structures of signals and PEMIs, a unit pulse atom was constructed to match PEMI, and sine atom, cosine atom and wavelet atom were chosen to match signal. Unlike common filtering ways of sparse decomposition, PEMI was firstly taken as a signal component, and all the atoms mentioned above were used to decompose the original signal. Secondly, only the components matched by sine atom, cosine atom and wavelet atom were used to reconstruct the unpolluted signal, and the component matched by the unit pulse atom was eliminated as PEMI. Simulations and applications testified that this technology can be used to filter strong PEMIs, the filtered signals not only have a high signal to noise ratio, but also retain details.

Key words:orthogonal matching pursuit; denoise; pulse electromagnetic interference (PEMI); multi-atom

在信号采集过程中，观测信号难免会受到白噪声的污染，而且还常常受到强电磁干扰，使信号淹没在噪声中，给信号的分析和处理带来极大的不便[1]。尽管通过一些昂贵和复杂的硬件设备能够对部分电磁干扰进行抑制[2]，但数字滤波的经济性和易用性具有更大的吸引力[3]。对于窄带或者具有统计规律的电磁干扰，可以通过小波、高阶统计、经验模态分解(Empirical Mode Decomposition，EMD)等方式进行滤波[4-6]。但对于随机的强脉冲电磁干扰，瞬间能量很大，在频域分布的范围广，现有方法还有些不足。另外，实测信号往往是多分量的，既有平稳成分也有非平稳成分，常规单基、单滤波器方法无法精确地提取有用信号[7]。

稀疏分解限制条件少、自适应性强、灵活高效[8]，为抑制强脉冲电磁干扰提供了一种新思路。常用的稀疏分解方法有匹配追踪[9](Matching Pursuit，MP)、正交匹配追踪[10](Orthogonal Matching Pursuit，OMP)和基追踪[11](Basis Pursuit，BP)。OMP和MP都是贪婪迭代算法，通过每次挑选出与信号内积最大的原子，实现自适应选取原子。但OMP将选用的基进行了正交化处理，比MP有更高的精度，往往有更高的计算效率，得到了许多学者的关注[10, 12-13]，因此本文选用OMP作为稀疏分解的方法。

稀疏分解构建原子库的方法比较灵活，针对不同的信号成分，可以选用多种原子的组合。由于有用信号中往往既有平稳成分也有非平稳成分，为了具有代表性，本文选用正弦原子和余弦原子匹配平稳成分，小波原子匹配非平稳信号成分，这种多原子的方式具有更强的自适应性[7]，提取信号更准确。常规稀疏分解除噪都是将分解后的残余当做噪声[9, 11, 14]，但这种方式不适用于强脉冲电磁干扰。为此，针对强脉冲电磁干扰结构特点，专门构造了单位脉冲原子。对信号进行稀疏分解时，将干扰当作信号成分进行提取，即选用正弦原子、余弦原子、小波原子和单位脉冲原子共同组成的原子库对信号进行分解，但在重构信号时仅使用正弦原子、余弦原子和小波原子匹配的成分进行重构，将单位脉冲原子匹配的成分和信号分解的残余剔除。这样不仅能够消除白噪声，而且能有效抑制脉冲电磁干扰。

1基于OMP的强脉冲电磁干扰滤波算法原理

1.1强脉冲电磁干扰滤波的数学模型

假设观测信号受到噪声污染，其数学模型为：

y=s+σz

(1)

式中：y为观测信号，是已知的；s为真实信号，是未知的；z为标准的高斯白噪声，σ为噪声的幅值，也是未知的。这是常规的噪声污染模型。

当观测信号还同时被强脉冲电磁干扰所污染时，其数学模型可以表示为：

y=s+p+σz

(2)

式中：p为脉冲电磁干扰，是未知的。因此对脉冲电磁干扰信号进行滤波相当于根据观测信号y滤除干扰p和白噪声σz，提取真实信号s。

1.2基于OMP的强脉冲电磁干扰滤波的算法过程

1.2.1过完备原子库的构建

构造的原子与有用信号越相似，OMP分解的效果往往就越好[12-13]。强脉冲电磁干扰发生时间短，瞬时能量大，在结构上与有用信号有明显的差别，根据其特点构造单位脉冲原子，假设信号的点数为N，第i个脉冲原子公式如下：

(3)

式中：1≤n≤N，且1≤i≤N。由公式(3)可知，脉冲原子i仅在第i点幅值为1，其余全为0，这与强脉冲电磁干扰瞬时大幅值的特性相似。

有用信号一般具有一定的规律，与强脉冲电磁干扰相比，有用信号变化相对平缓。为了具有通适性，选用正弦原子、余弦原子和小波原子匹配有用信号。正弦、余弦原子与周期性的平稳信号相似，用于匹配平稳成分。小波原子的适应性较强，用于匹配有一定突变的非平稳成分，为了更明显地区别于单位脉冲原子，仅选用低频小波基，本文选用coiflets 3小波，分解层数为4，即仅选用了1～4层的低频小波基。将正弦原子、余弦原子、小波原子所构成的原子库用D1表示，使用D1重构的信号为真实信号；脉冲原子构成的原子库用D2表示，D2所匹配的成分作为脉冲电磁干扰；它们共同构成的原子库用D表示。

需要说明的是，这种方法不仅对脉冲电磁干扰有效，而且对于可以使用脉冲原子稀疏表示或发生时间很短的其他类型的电磁干扰也有效，比如发生时间较短的类方波干扰或三角波干扰等。另外，可以根据实际的有用信号的特点更换原子库D1中的原子，可以得到更好的分解效果。

1.2.2OMP计算过程

OMP是一种将信号逐步分解的过程。首先，在原子库中选取与信号最匹配的原子，然后将匹配的成分从原信号中减去得到残余；在之后的迭代中，每次选择与残余成分最匹配的原子后，都首先将所有选中的原子正交化，之后重新在原始信号上进行投影，提取匹配部分并留下残余；按照这种方式反复迭代，直到残余信号的能量小于设定的阈值或达到最大迭代次数[10]。

OMP能保证残余与所有已选原子正交，比MP收敛的更快，对原信号的表示也更稀疏[10]；相对于BP，OMP作为一种纯贪婪迭代算法所需内存和计算时间都要小许多，对于长度为L，稀疏度为K的信号，K≪L，使用OMP计算的复杂度为LK3，因此应用更广泛[10, 12-13]。

(1)设y为待处理的信号序列，信号残余R0=y，已选原子的集合ψ-1为空集，迭代次数n=0。

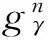
(4)

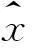
(5)

通过以上方式，可以有效地将白噪声和脉冲电磁干扰滤除，为进一步对信号进行分析和处理奠定了基础。

2仿真实验与对比分析

为了验证上述滤波方法的性能，构造以下仿真信号。原始信号s=s1+s2+s3，其中s1(t)=cos(20πt)，为正弦信号；s2(t)=[1+sin(40πt)]cos(200πt)，为调幅信号；s3(t)=5e-10tcos(60πt)，模拟非平稳成分。此外，给原始信号添加白噪声z和模拟脉冲电磁干扰p1、p2，其中p1为10个随机发生的脉冲信号，幅值是[10,11]或者[-10,-11]之间的随机数，模拟强脉冲电磁干扰；p2为4个宽度为5的强电磁干扰，幅值是[20,21]之间的随机数，模拟类方波电磁干扰；噪声z为信噪比(Signal to Noise Ratio，SNR)为4的白噪声。信号采样频率为1 024 Hz，采样点数为500。

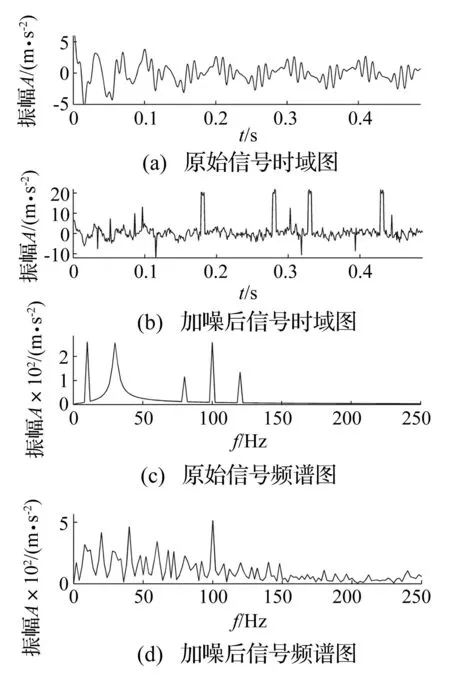
图1　原始信号与加噪信号的时域图和频谱图 Fig.1 The waveforms in time domain and frequency domain of original signal and polluted signal

图2　不同滤波方法去噪效果对比图 Fig.2 The denoising results of different methods

原始信号与加噪信号的波形及频谱图如图1所示。由图中可以看出，加噪信号在时域和频域都发生了畸变，需要将干扰成分滤除才能正确分析信号。为了充分验证本文方法的有效性，采用1.2节所述信号重构方案，分别采用MP、OMP和BP对信号分解。此外还采用常规去噪方法，包括小波[4]、EMD[15-16]以及数学形态法[17-18]进行降噪，其中小波选用coiflets 3小波，分解层数为4，数学形态法中的结构元素为幅值为0的平结构元素，长度为6。这些方法的去噪结果如图2所示，相对应的频谱如图3所示，并采用SNR和均方误差(Mean Square Error，MSE)对这些方法进行评价，如表1所示。

由图1～图3和表1可知，得益于本文所提出的原子重构方案以及稀疏分解的自适应性，利用MP、OMP和BP三种方法恢复原始信号的效果较优，并且OMP在时域、频域、SNR和MSE评价指标中都是最优的，表现出了优良的特性。客观来说，BP也是一种优异的稀疏分解方法[11]，但使用BP去噪时需要准确估计噪声的大小，否则会影响重构效果；此外，BP分解时需要使用所有原子，所占内存和需要的计算时间都会大大增加，在这个仿真实验中，BP所用时间是OMP所用时间的20倍，效率较低。由分解结果可以看出，BP在SNR和MSE值方面略优于MP，但BP和MP都未能在频域正确恢复出原始信号。而常规去噪方法小波和EMD则未能滤掉电磁干扰，这是由于它们都认为噪声在一些转换域中的能量会较小，将小于一定阈值的信号当做噪声去除，显然无法适应于大幅值、高能量的强脉冲电磁干扰信号。而数学形态法尽管能一定程度上滤除脉冲电磁干扰，但去噪后的信号发生了畸变，丢失了细节。此外，小波、EMD和数学形态法去噪后的信号在频域都丢失了一些重要分量，并包含大量的噪声，未能正确恢复原信号。

仿真实验结果说明，常规去噪方法不适用于强脉冲电磁干扰信号，采用本文所提出的滤波方法能够有效滤除脉冲类强电磁干扰和白噪声，并且在时域和频域都有较好的表现。

图3　不同滤波方法去噪后的频谱图 Fig.3 Spectra of filtered signals by different denoising methods

去噪方法SNRMSEMP4.51.0OMP8.30.6BP5.50.8小波-8.44.2EMD-8.84.4数学形态法4.21.0

3在液压泵压力信号中的应用

图4为液压泵压力测试平台，实测压力信号不仅受到外界的白噪声干扰，还受到变频器、电机和线路的强脉冲电磁干扰。测试时液压泵转速为900 r/min，液压泵有7个柱塞，因此转频为15 Hz，压力脉动基频为105 Hz。

图4　液压泵压力信号采集平台 Fig.4 The test rig of pressure signal acquisition for hydraulic pump

原始压力信号和去噪后信号的时域、频域波形如图5所示。由图中可以看出，原始压力信号已经被脉冲电磁干扰和白噪声严重污染，看不到油压脉动，并且其频谱图中也包含很多的噪声，使得频谱分析可信度降低。采用本文方法进行滤波后，不仅滤除了强脉冲电磁干扰，精确地恢复了压力变化过程，还保留了压力脉动的细节和突变。此外，去噪后的信号频谱图也没有了噪声，而且显示更多的转频和压力脉动的倍频。这些结果表明，本文所提出的去噪方法能够有效滤除强脉冲电磁干扰和白噪声，同时能完整保留有用信号的细节部分，满足了实际需要。

图5　原始压力信号与去噪结果对比 Fig.5 The comparison between original pressure signal and denoised signal

4结论

针对强脉冲电磁干扰的结构特征构造的单位脉冲原子能够很好地匹配脉冲干扰，借助于本文设计的信号重构方案，有效地消除了强脉冲电磁干扰和白噪声，突破了常规方法的思维定势，为滤波提供了一个新的思路。仿真实验对比和实例应用说明，常规去噪方法抑制强脉冲电磁干扰尚有不足，而本文所提出的基于OMP的多原子的滤波方法能够对脉冲电磁干扰以及短时强电磁干扰都有良好的抑制作用，同时很好地保留了信号的细节，克服了常规去噪算法的不足。当应用本文滤波方法时，可以根据实际信号的特点改变原子库D1的组成，以得到更好的去噪效果。

参考文献

[1]Liang J, Wang Y, Huang Y, et al. Electromagnetic interference shielding of graphene/epoxy composites[J]. Carbon, 2009, 47 (3): 922-925.

[2]Al-Saleh M H, Sundararaj U. Electromagnetic interference shielding mechanisms of CNT/polymer composites[J]. Carbon, 2009, 47 (7): 1738-1746.

[3]Tarateeraseth V, See K Y, Canavero F G, et al. Systematic electromagnetic interference filter design based on information from in-circuit impedance measurements[J]. Electromagnetic Compatibility, IEEE Transactions on, 2010, 52(3): 588-598.

[4]Aggarwal R, Rathore S,Singh J K, et al. Noise reduction of speech signal using wavelet transform with modified universal threshold[J]. International Journal of Computer Applications, 2011, 20(5):14-19.

[5]Inoue T, Saruwatari H, Takahashi Y, et al. Theoretical analysis of musical noise in generalized spectral subtraction based on higher order statistics[J]. Audio, Speech, and Language Processing, IEEE Transactions on, 2011, 19 (6): 1770-1779.

[6]Wu Z, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in adaptive data analysis, 2009,1(1): 1-41.

[7]Feng Z, Chu F. Application of atomic decomposition to gear damage detection[J]. Journal of Sound and Vibration, 2007, 302 (1): 138-151.

[8]Olshausen B A. Emergence of simple-cell receptive field properties by learning a sparse code for natural images[J]. Nature, 1996, 381 (6583): 607-609.

[9]Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. Signal Processing, IEEE Transactions on, 1993, 41(12): 3397-3415.

[10]Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. Information Theory, IEEE Transactions on, 2007, 53(12): 4655-4666.

[11]Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61.

[12]Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. Information Theory, IEEE Transactions on, 2012, 58(2): 1094-1121.

[13]Needell D, Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2007, 9(3): 317-334.

[14]Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2009, 31(2): 210-227.

[15]Flandrin P, Rilling G, Goncalves P. Empirical mode decomposition as a filter bank[J]. Signal Processing Letters, IEEE, 2004, 11(2): 112-114.

[16]Huang N E, Wu M L, Long S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 2003, 459(2037): 2317-2345.

[17]沈长青,谢伟达,朱忠奎, 等. 基于 EEMD 和改进的形态滤波方法的轴承故障诊断研究[J]. 振动与冲击, 2013, 32 (2): 39-43.

SHEN Chang-qing, XIE Wei-da,ZHU Zhong-kui, et al.Rolling element bearing fault diagnosis based on EEMD and improved morphological filtering method[J].Journal of Vibration and Shock,2014,33(4):11-16.

[18]钟先友,赵春华,陈保家,等. 基于形态自相关和时频切片分析的轴承故障诊断方法[J]. 振动与冲击, 2014,33(4):11-16.

ZHONG Xian-you, ZHAO Chun-hua, CHEN Bao-jia, et al.Bearing fault diagnosis method based on morphological filtering,time-delayed autocorrelation and time-frequency slice analysis[J].Journal of Vibration and Shock,2014,33(4):11-16.