基于奇异值分解的银行客户数据隐私保护算法研究
2017-03-27季文韬
摘 要 如何在保护客户数据隐私的前提下进行有效的数据挖掘,已经成为金融业数据挖掘领域的重要课题。用矩阵的奇异值分解进行数据扰动,不仅能消除数据噪音,还能获得准确的聚类效果。本文提出了一种奇异值分解的聚类算法,实验表明算法能有效的保护客户数据隐私,而且保留了聚类分析的准确特征。
【关键词】奇异值分解 隐私保护 聚类分析
随着数据挖掘技术和机器学习算法的快速发展,数据隐私保护问题已经越来越引起人们的关注。目前的隐私保护方法主要分为两类:
(1)对原始数据值进行扭曲、扰动、随机化和匿名化,使数据使用者不能得出数据的原始值。
(2)修改数据挖掘算法,使分布式数据挖掘中的参与者在不知道确切数据值的情况下仍能得出数据挖掘的结果。
数据扰动是隐私保护数据挖掘应用的重要组成部分,我们利用奇异值分解(Singular value decomposition)SVD)对保密数值属性进行扰动,并在矩阵分解的基础上进行隐私数据聚类。我们所提出的的奇异值分解聚类方法,不仅可以满足保护敏感数据属性的要求,同时保留K-means聚类分析的一般特点,能得到准确的数据模型和分析结果。
1 算法的理论基础
1.1 K-均值聚类算法
K-均值聚类算法是一个将包含有n个对象的数据集划分成k 个聚类的过程,使同一聚类中的对象属性相似度较高,而不同聚类中的对象属性相似度较小。聚类分析的基本指导思想就是最大程度地实现类中对象相似度最大,类间对象相似度最小。
1.2 奇异值分解
奇异值分解在数据挖掘的应用中,特别是在文本挖掘中并不是新技术,但在隐私保护的数据扰动中的应用是最近兴起的。一个奇异值分解的显著特点是在降维压缩数据的同时维持主要的数据模式。矩阵分解的主要目的是从原始数据集获得一些低维的,对象和属性的近似关联的数据结构。
奇异值分解的显著特点是在降维压缩数据的同时保护了主要的数据模式。在隐私保护金融数据挖掘应用中,扰动的数据集Ak可以在同时提供数据隐私保护,还保留了原始数据的可用性,使其真实地表现原始的数据集结构。
奇异值分解(SVD)是一种常见的数据挖掘矩阵分解方法和信息检索方法。它开始被用来降低数据集的维度。文献[3]提出了用SVD进行数据扰动的技术,在文献[4]中,SVD技术是用来扰动数据集的模式部分。
2 SVD-clustering模型及算法
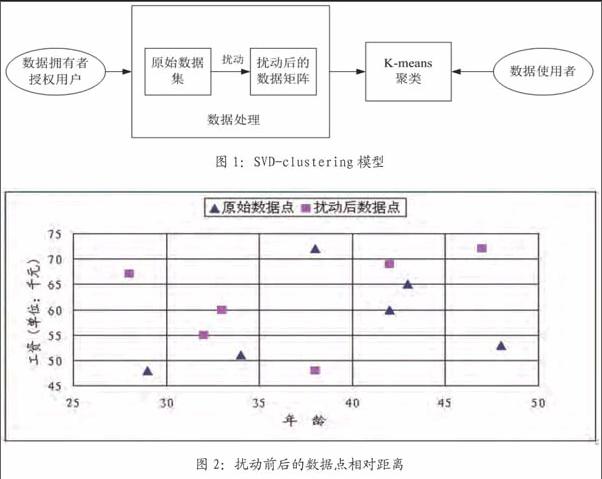
SVD-clustering模型包含兩部分:数据扰动部分和数据的聚集部分。模型如图1所示。我们假设只有数据的拥有者和授权用户才可以对数据进行处理。经过数据扰动,原始的数据集转换成完全不同的数据矩阵,数据使用者利用K-means聚类等数据挖掘算法对扰动的数据进行检索。因为数据使用者未经授权不能得到原始数据,这样,包含隐私保密信息的原始数据就得到了保护。
2.1 SVD-clustering算法流程
输入:初始矩阵D,划分的聚类的数目K
输出:转换后的矩阵D',聚类结果
(1)在矩阵D中找出需要保密的数据属性序列(ai)i=1,2,…,n.形成一个新的矩阵A,A=[a1, a2,…,an];
(2)用SVD算法对矩阵D进行分解SVD(A)=UWVT;
(3)找出扰动后的矩阵AK=UkWkVkT;
(4)用Ak的值更新数据库D,形成新的矩阵D′;
(5)在矩阵 D′中对保密数据的属性进行聚类分析。
2.2 算法示例
样本数据如表1所示,在隐私保护的第一阶段采用匿名保护,用编号代替被采样者,假设已经去除了标识符(如姓名、身份证号码、地址等)。在这个样本中我们比较关注年龄和年薪两个属性,假设数据的使用者想利用这些人的年龄和年薪对他们进行分类。但是这些属性值都是保密的信息,即要对这两个属性进行隐私保护。
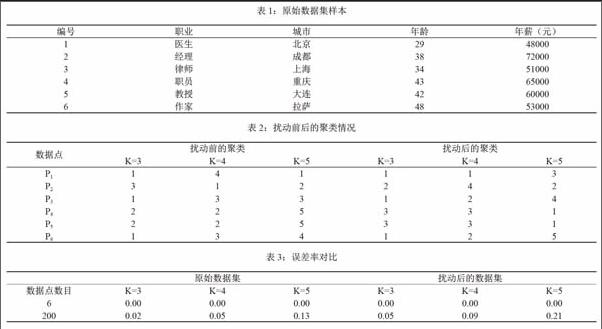
为了达到隐私保护的目的,我们利用SVD-clustering模型对数据进行扰动。图2显示经过扰动后各个数据对象在扰动前后聚类中的相对距离。
3 实验结果分析
为简单起见,我们只考虑转化两个隐私数据属性,年龄和年薪。每次聚类包含6个数据点,在表2中,分别表示包含年龄和工资两个属性的六个数据点。在扰动前,当K=3时,对象1,3,6在聚类1中,对象4,5在聚类2中,对象2在聚类3中,在数据扰动后,当K=3时,数据1,3,6在聚类1中,对象2在聚类2中,对象4,5在聚类3中。
实验的效率根据原始数据和扰动后数据的合法点聚类检测出来的。在进行数据扰动后聚类的簇元素和原始数据聚类后的簇元素应该一致,但是在数据扰动过程中可能存在一些潜在的问题:一些噪音点中断了聚类过程;一个聚类中的数据点变成噪音点;一个数据点从一个聚类转移到另一个聚类。由于我们采用的K-means聚类算法已经消除了噪音,所以我们验证结果的时候只考虑第三种情况。
3.1 误差率分析
其中,N 代表原始数据集 D中点的个数,k 为聚类的个数,D'为扰动后的数据集,|Clusteri(D)|代表第 i个聚类中的合法数据点的个数。从表3中可以看到,利用SVD-clustering算法得到的误差率在0.1% 左右,可以证明我们的算法在数据扰动前后聚集的准确性非常好。
3.2 相对误差分析
当一个数据矩阵扰动后,它的属性值也发生改变,数据值的变化可以用范数的相对误差表示。这样,可以用RE(Relative Error)表示原始值D到扰动后的属性值D′的变化。
其中||D||F是矩阵D的欧式范数,D'为扰动后的数据集。可以看出,RE的数值越大,表明数据扰动的程度越大,即数据的保密性能越好。
4 结论
我们提出一个奇异值分解的聚类方法,用来扰动保密数值的属性,以满足银行客户隐私保护的要求,同时保留K-means聚类分析的一般特点.实验结果表明,该方法在高准确性隐私保护应用中非常有效,保证聚类挖掘结果正确性的基础上,对数据集中的敏感属性也进行了很好的隐私保护。
参考文献
[1]R.Agrawal,R.Srikant.Privacy-preserving data mining.in:Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data,2000,439-450.
[2]J.Wang,J.Zhang,W.Zhong,S.Xu,A novel data distortion approach via selective ssvd for privacy protection.2009.
[3]V.Verykios,E.Bertino,I.Fovino,L.Provenza,Y.Saygin,Y.Theodoridis. State-of-the-art in privacy preserving data mining.ACM SIGMOD Record,2014,3(01):50-57.
[4]L.Hubert,J.Meulman,W.Heiser.Two purposes for matrix factorization: a historical appraisal.SIAM Review,2009,42(04):68-82.
[5]张国荣,印鉴.应用等距变换处理聚类分析中的隐私保护[J].计算机应用研究,2015(07):83-86.
[6]黄伟伟,柏文阳.聚类挖掘中隐私保护的几何数据转换方法[J].计算机应用研究,2006(06):180-184.
作者簡介
季文韬(1986-),男,河南省南阳市人。主要研究方向为隐私保护数据挖掘。
魏巍 (1992-),男,河南省南阳市人。主要研究方向为数据处理。
作者单位
1.中国农业银行成都青羊支行 四川省成都市 610015
2.电子科技大学成都学院通信与信息工程系 四川省成都市 610500
