考虑地形条件影响的车桥耦合系统地震响应分析
2016-01-15乔宏,夏禾,杜宪亭等
第一作者乔宏女,博士生,1989年9月生
通信作者夏禾男,教授,1951年4月生
考虑地形条件影响的车桥耦合系统地震响应分析
乔宏,夏禾,杜宪亭,南勇
(北京交通大学土木建筑工程学院,北京100044)
摘要:研究局部地形条件对地震作用下车桥耦合系统动力响应的影响。依据黏弹性边界理论,利用ANSYS建立了可以考虑局部地形条件的三维场地模型,并通过将输入地震动转化为作用于人工边界上的等效荷载来实现波动输入,得到考虑地形影响之后的桥梁各支点地震动时程曲线。将地震激励以速度时程和位移时程形式作用到结构上,编制计算程序,进行多点地震激励作用下的车桥耦合分析。以列车通过总长480 m的实际桥梁为算例,对考虑局部地形影响的车桥耦合系统地震响应进行了仿真分析。结果表明:考虑地形影响后,地震作用下桥梁和车辆的动力响应在峰值大小和峰值出现时间上均发生了改变,且其变化规律随桥梁所处的地形类型的不同而有所差别,说明进行车桥耦合系统地震响应分析时考虑局部地形影响的必要性。
关键词:车桥耦合系统;动力分析;地震作用;地形效应;黏弹性人工边界
基金项目:国家973计划项目(2013CB036203);国家自然科学基金项目(51208027);中央高校基本科研业务费专项资金资助 (2014YJS095)
收稿日期:2014-11-21修改稿收到日期:2015-01-20
中图分类号:U441
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.17.012
Abstract:The influences of topography on the dynamic response of a train-bridge system under earthquake were studied. According to the theory of visco-elastic artificial boundary, a 3-D finite element site model accounting for topographic effects was established by using ANSYS. The process of wave input was realized by converting the seismic time history into equivalent loads acting on the artificial boundary, the seismic time history curve at each support of the bridge was obtained. The dynamic analysis of the train-bridge coupled system subjected to multi-support seismic excitations was performed, the velocity and displacement time histories of seismic excitations were exerted on the bridge supports. With a train passing through a 480m-bridge as a case study, the dynamic responses of the train-bridge coupled system under earthquakes considering local topography were simulated. The results showed that the peak value and the time of peak appearance for the dynamic response of the train-bridge system vary and the variation laws are different due to different topographic effects, so it is necessary to consider topographic effects in dynamic analysis of train-bridge coupled systems under earthquakes.
Seismic response analysis of a train-bridge coupled system considering topographic effects
QIAOHong,XIAHe,DUXian-ting,NANYong(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)
Key words:train-bridge coupled system; dynamic analysis; earthquake action; topographic effects; visco-elastic artificial boundary
近些年来,随着铁路事业的飞速发展,我国的铁路桥梁数量与日俱增,在地震易发区列车在桥上行驶时遭遇突发地震的可能性大大提高。地震作用下车桥耦合问题已经成为当前研究的热点之一[1-4]。在地形条件复杂的山区,实际地震中存在的地形对地震作用的放大现象引起了人们的注意。Celebi通过对1985年智利地震(Central Chile,M7.8)余震的地震实测数据进行观察发现,山脊顶及陡崖受到的地震破坏作用相对较大[5]。在该次地震中,沿两个山脊和紧邻一个山脊的山谷中,由同一承包商建设的钢混框架结构公寓的震害截然不同,建在山脊上的公寓破坏严重,而建在山谷场地中的公寓没有遭到破坏[6]。Jibson实测了五次地震下日本一座山脉各点的加速度峰值,发现相较于山脚,山顶处的加速度峰值放大了1.8~5.5倍。我国汶川地震中庙子坪大桥、百花大桥的破坏除了地震烈度高的原因外,所处的复杂地形或许也是其中因素之一[8]。因此,局部地形条件对车桥耦合系统地震响应的影响值得关注。
到目前为止,国内外的相关研究主要集中于局部场地条件对桥梁地震响应的影响分析[9-11],极少考虑地形条件对车桥耦合系统地震响应的影响。
本文基于黏弹性人工边界理论和有限元方法,建立了能够反映桥梁局部场地条件的三维分析模型,将输入地震动转化为作用于人工边界上的等效荷载来实现波动输入,得到结构支撑处地震动时程。将考虑地形影响之后的桥梁支撑处地震动作为外激励施加到车桥耦合振动系统上,以某实际工程为例,编制相关计算程序,研究了地形条件对地震作用下车桥系统动力响应的影响规律。
1考虑地形条件影响的地震动
采用有限元软件实现地震动输入问题时,一般是从无限介质中切取出有限尺寸的计算区域,通过在有限区域的边界上引入适当的人工边界条件来实现无限区域的模拟。建立人工边界条件的关键在于所建立的边界上不存在能量反射。Liu等[12]提出的三维黏弹性人工边界除满足以上条件外,还具有计算精度高、计算稳定性好,应用方便等优点,因此本文在建立场地模型时,选择了黏弹性人工边界。
1.1外源输入的等效边界力法
文献[13]中将输入地震动转化为作用于人工边界上的等效荷载的方法来实现波动输入,其人工边界的法向和切向等效荷载分别为:
KBNu0(xB,yB,t)
(1)
KBTv0(xB,yB,t)
(2)
式中:u0(x,y,t)和v0(x,y,t)分别为入射波的法向和切向位移;σ0(x,y,t)和τ0(x,y,t)分别为法向应力和切向应力;xB和yB是人工边界节点坐标,KBN、KBT、CBN、CBT分别为黏弹性人工边界的法向、切向弹簧系数和阻尼系数[12]。
1.2等效地震力计算
地震时一般震源较深,且地震波向上传播过程中要经过各种不同岩层的折射,导致地震波到达地表时已接近垂直入射。因此,本文假设地震波以平面波形式自底边界竖直入射,且竖直入射的平面P波和S波的位移时程分别为uP(t)和uS(t)。直角坐标系的x-y面平行于底边,z方向指向有限域,见图1。

图1 地震波竖直入射模型 Fig.1 Vertical incidence model of seismic wave
假设S波沿x轴方向振动,则由波动传播规律及波场应力状态可以解析得到各人工边界节点的等效地震荷载[14-15],即:
(1)P波入射
(3)
(4)
(5)
(6)
(7)
(2)S波入射
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
式中:各节点等效地震荷载的下标代表应力方向;上标代表节点所在边界的外法线方向;Δt1~Δt4分别代表入射P波、地表反射P波、入射S波及地表反射S波的时间延迟;l为节点到底边界的距离;L为底边界到地表的距离;A为边界节点的人工边界影响面积,具体取值参考文献[12],λ、ρ、cp、cs分别为介质的一阶拉梅常数、密度、纵波波速和横波波速。
1.3黏弹性人工边界的实现
以ANSYS软件为例,场地介质可以利用Solid45单元模拟,黏弹性人工边界的弹簧和阻尼器可以通过在每一个边界节点添加一端固定的Combin14单元模拟。
2地震荷载作用下车桥系统动力分析模型
如图2所示为车桥耦合系统的示意图,它由桥梁子系统和车辆子系统所组成。假定列车沿桥梁纵向匀速行驶,且桥梁各支撑处地震地面运动不一致。车桥系统绝对坐标系满足右手准则,其中,y方向为桥梁纵向,x方向为桥梁横向,z方向为竖直方向,为方便计算,在这里取向下为正方向。假设地震只对桥梁子系统产生直接影响,对于车辆子系统的影响,则通过基础、桥墩、桥面、轨道传递给车辆子系统,即地震对车辆子系统的影响可以通过轮轨关系实现,无需在车桥耦合动力分析模型中特别考虑地震对车辆子系统的影响。
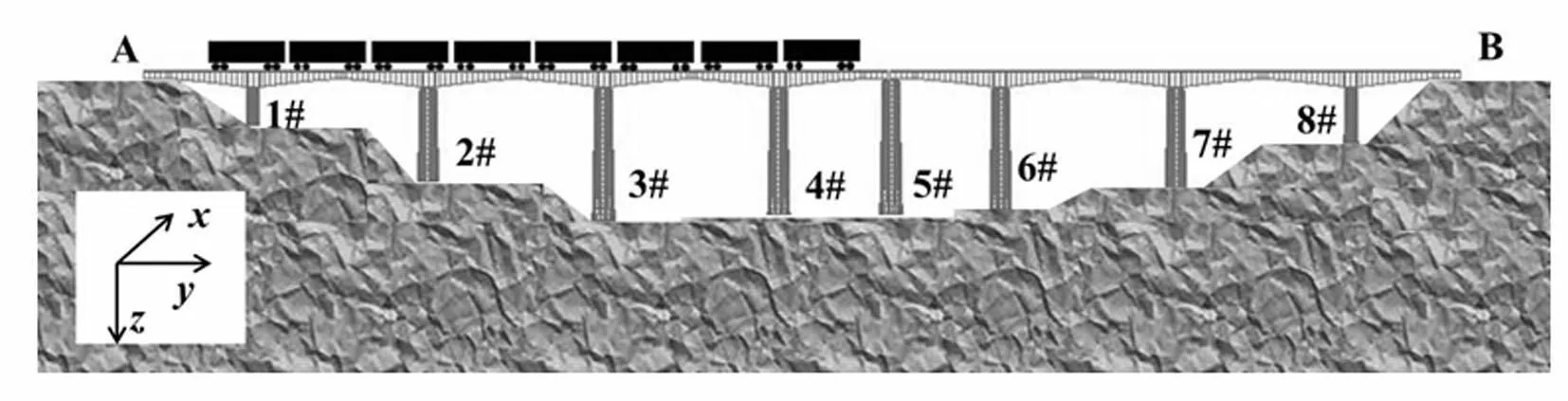
图2 车桥耦合系统 Fig.2 The bridge-train system
如果采用有限元法描述地震作用下的车桥耦合振动,则在绝对坐标系下,车辆、桥梁子系统的动力平衡方程分别为[2]:
(16)
(17)
将式(17)中的第一项展开,可以得到有限元法描述下的桥梁结构自身各点的运动平衡方程,即:
(18)
由于Msb常被忽略,因此,式(18)变为:
(19)
其中等号右边的前两项即为地震作用到桥梁结构上的荷载。
将式(19)利用振型分解法进行模态降阶,可以得到:
(20)
式中:φi和qi为质量归一化的第i阶振型和广义坐标;ωi和ξi分别为第i阶频率和阻尼比;n为分析中所用到的桥梁模态数;R为影响矩阵,R=-K-1ssKsb。
式(16)和式(20)构成了地震作用下车桥耦合系统动力平衡方程组,通过编制相应的计算程序,迭代求解这两式即可得到地震作用下车桥耦合系统的动力响应。
3算例
为研究地形条件对车桥耦合系统地震响应的影响,选取某实际桥梁作为算例进行分析。
桥梁全长为480 m,由两联连续梁跨组成,跨度布置为(40+64+64+64+40) m+(40+64+64+40) m。桥梁梁体采用单箱单室变高度直腹板箱型截面,主墩墩顶5 m范围内梁高相等,为6.05 m,见图3(a);跨中及边墩墩顶现浇段梁高3.05 m,梁体截面见图3(b)。梁底曲线为二次抛物线。
桥墩为圆端形空心墩,墩顶3 m范围,墩底3m范围为实体段。桥墩高度分别为13.5 m、34 m、48.5 m、46 m、49 m、45.5 m、36 m和20 m。桥梁所处的地形条件见图2。沿着桥梁纵向,将桥梁桥墩分别编号为1#,2#……8#,两个桥台分别命名为A桥台和B桥台。
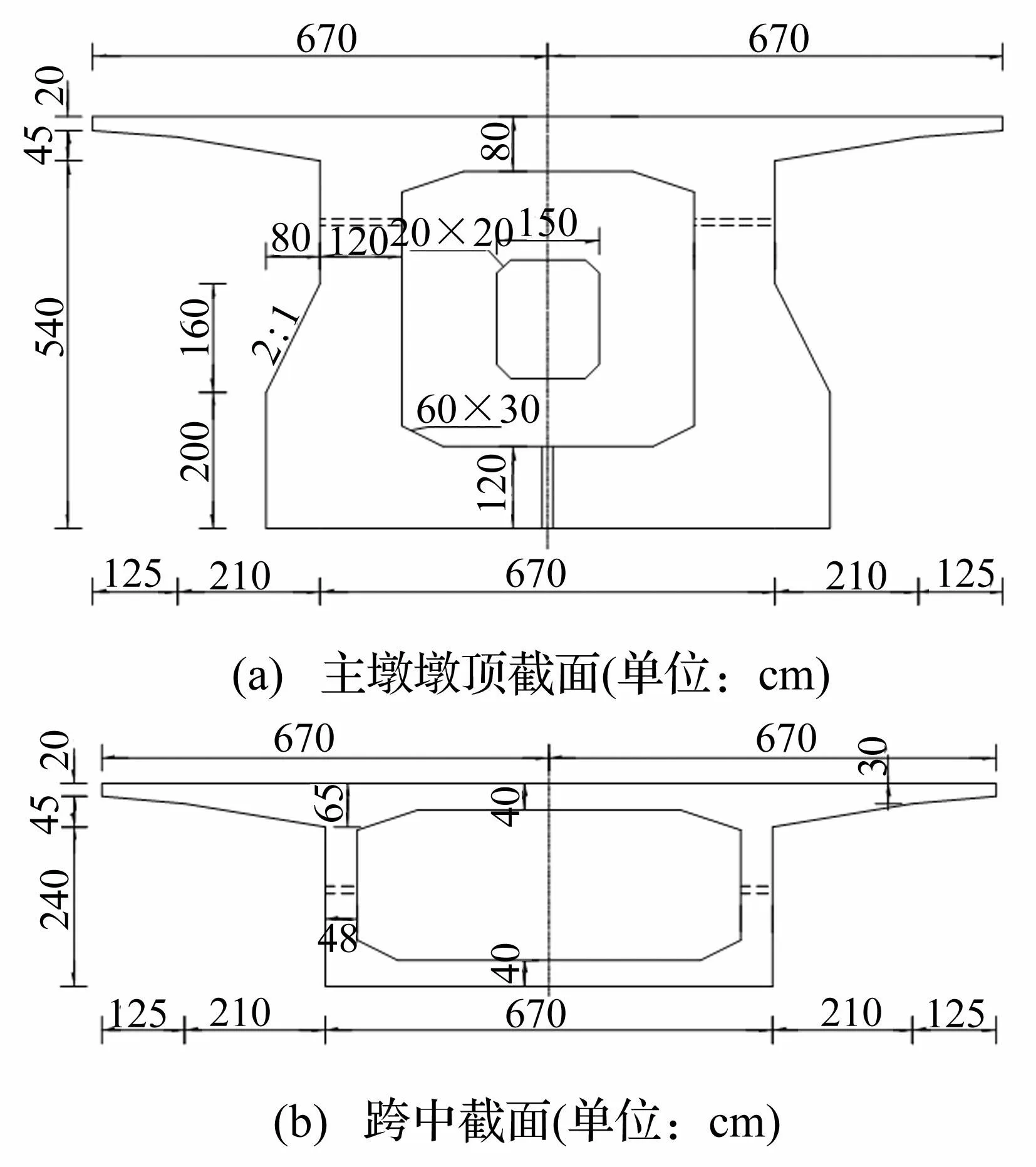
图3 桥梁截面示意图 Fig.3 Sections of the bridge
桥梁有限元模型采用梁单元建立,边界条件取为墩底全部固结,梁体和桥墩之间设置主从节点。其中,在两联连续梁连接处,两联梁体分别设置从属节点,均从属于共用桥墩上的主节点。建立的有限元模型见图4(a)。取桥梁的前100阶模态进行车桥耦合分析,编制计算程序,在计算过程中桥梁各阶模态的阻尼比均假定为0.05。
对所建桥梁有限元模型进行模态分析,可以得到该桥梁的自振频率和振型,其中前8阶的自振频率及模态振型见图4(b)。

图4 桥梁有限元模型及各阶自振特性 Fig.4 FE model and mode parameters of the bridge
分别假设该桥位于河谷处和两山峰之间,建立ANSYS场地模型,分析地形条件对车桥耦合系统地震响应的影响。
桥梁所在场地有限元模型采用Solid45单元模拟,单元尺寸设为8,土层密度ρ=2 610 kg/m3,弹性模量为E=5 GPa,泊松比为0.26,阻尼比为0.05,P波的传播速度为cp=1 530 m/s。如前文所述利用Combin14单元建立黏弹性边界,最终建立场地有限元模型见图5,其中,河谷地形和山峰地形的有限元模型尺寸分别为640 m×160 m×160 m和1 760 m×160 m×260 m。
地震波选取某实际地震中记录的地震加速度时程,将其进行积分并消除基线偏移,得到该地震的速度时程和位移时程曲线,见图6。分别假设该波为平面P波和平面S波,根据式(3)~(7)及式(8)~(14)求得各节点需输入的节点等效荷载,得到考虑地形条件影响的桥梁各支点竖向和横向地震动时程。将地震激励以速度时程和位移时程形式作用到结构上,进行多点激励作用下地震-车-桥耦合分析,研究地震作用下车桥耦合系统的竖向和横向动力响应。
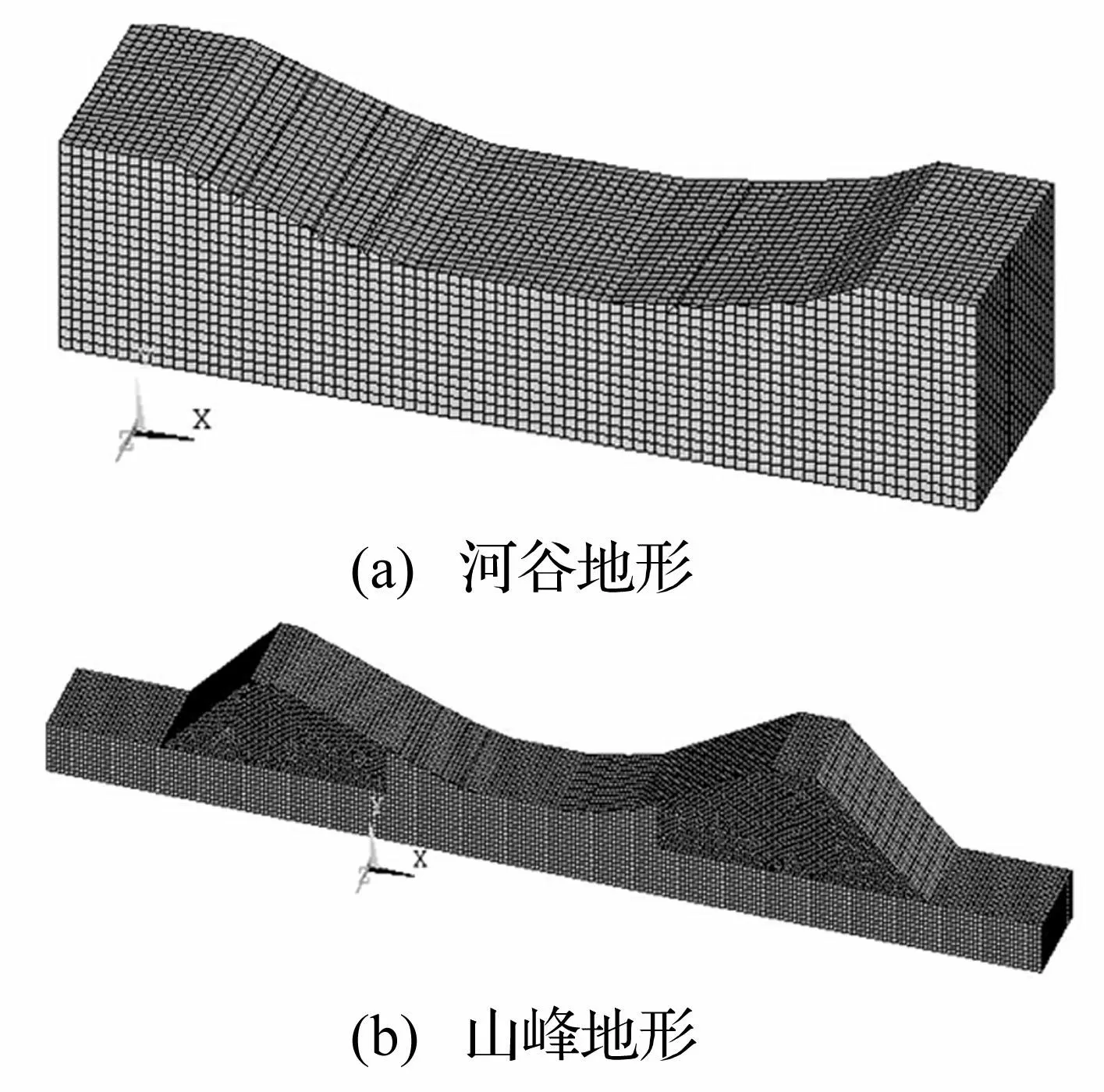
图5 场地有限元模型 Fig.5 Finite element model of local topography

图6 地震动时程 Fig.6 Seismic time history
车辆模型选择ICE3高速列车,共有8节,并采用3动1拖的编组设置。每节车采用刚体-弹簧-阻尼离散模型,车体之间视为相互独立的单元,采用达朗贝尔原理推导其质量矩阵、阻尼矩阵和刚度矩阵,形成运动方程[16]。分析车速为150 km/h。轮轨接触关系采用密贴假定,轨道不平顺采用德国低干扰谱,其高低不平顺见图7。
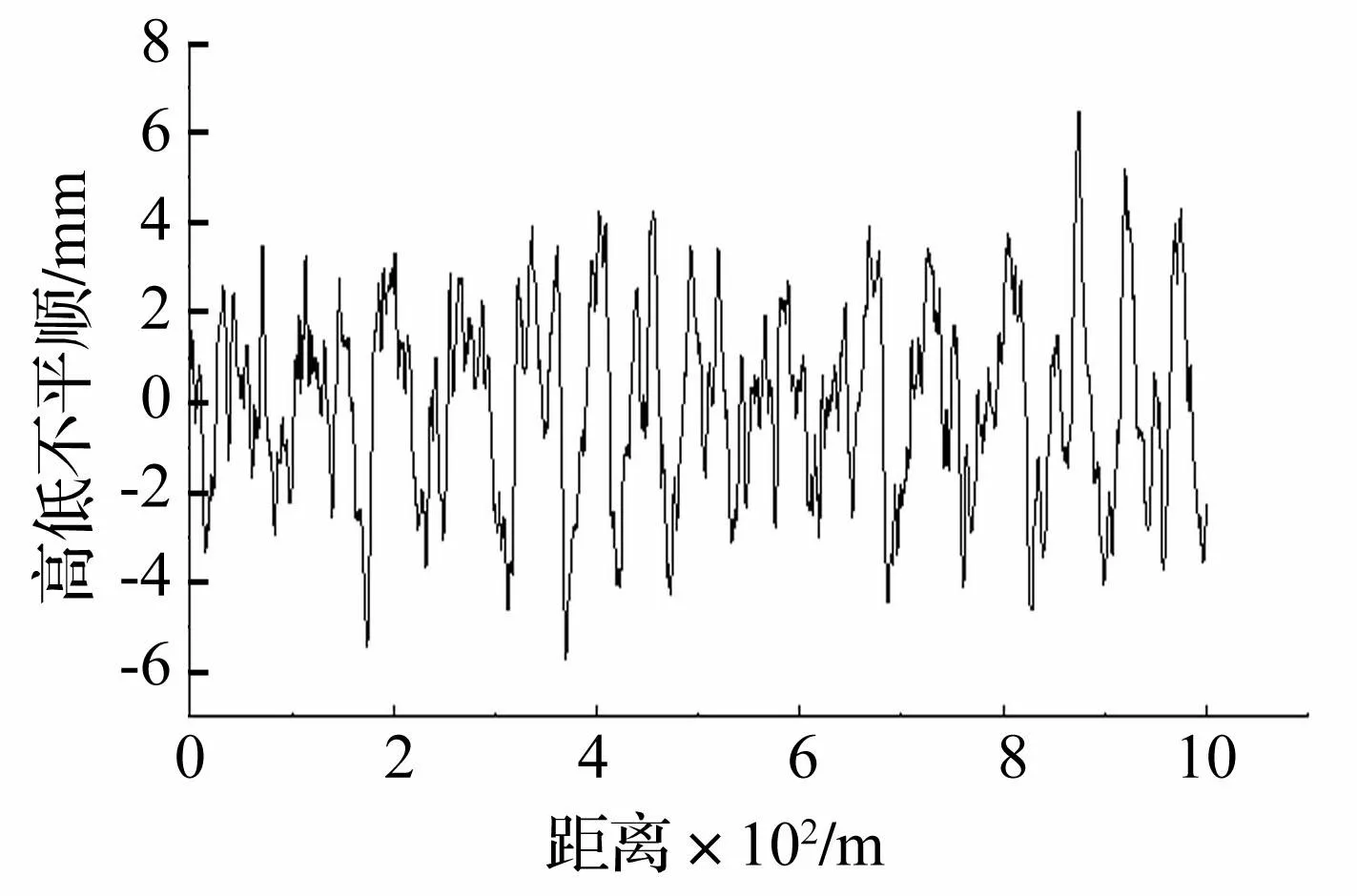
图7 轨道高低不平顺 Fig.7 Vertical track irregularity curve
假设列车上桥时刚好发生地震。依据以上条件编制地震多点激励作用下车桥耦合计算程序,进行考虑地形条件影响的车桥耦合系统地震响应分析。
3.1桥梁各支点地震动时程
计算中,分别采用考虑与不考虑地形影响的两种场地模型。在不考虑地形效应影响的模型中把模型的上表面取为自由水平表面[11],建立有限元模型,获取桥梁各支点的地震动时程。
如表1所示为桥梁各支点处考虑地形效应影响后的地震动位移时程最大值与不考虑地形效应时地震动位移时程最大值的比值。其中,横向位移最大值按+x和-x方向分别考虑,而竖向位移最大值按+z和-z两个方向分别考虑,见图2。从表中可以看出,对于横向位移,考虑地形效应影响后,河谷地形中各支点横向位移最大值在两个方向上均减小;而山峰地形中,+x方向各支点横向位移最大值增大,-x方向各支点横向位移最大值减小;对于竖向位移,河谷地形中各支点两个方向上竖向位移最大值均减小,而山峰地形中各支点两个方向上竖向位移最大值均增大。
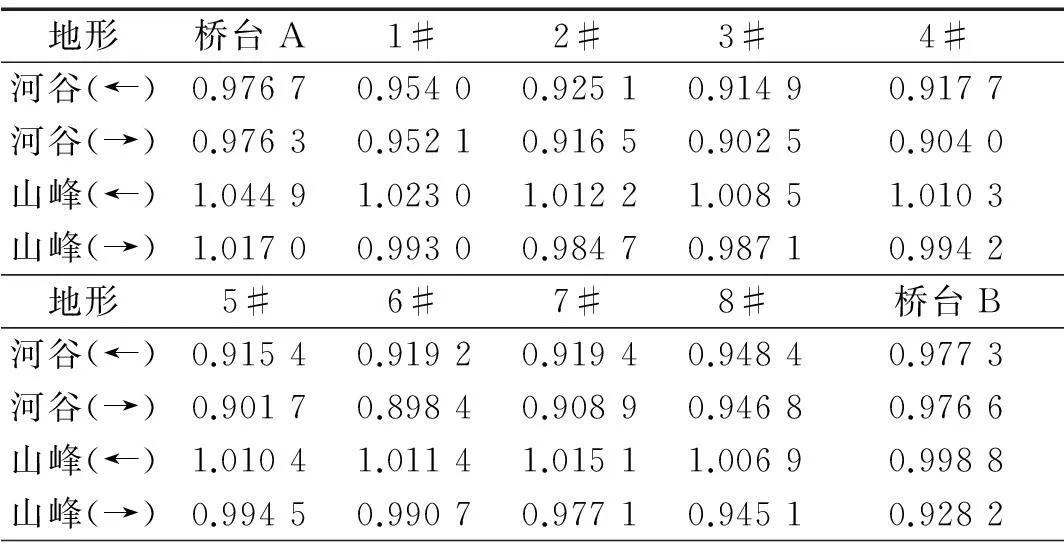
表1 桥梁各支点地震动位移时程最大值比值

(b)竖向
3.2河谷地形下P波入射条件下动力分析结果
图8、图9分别给出了河谷地形中车速150 km/h条件下P波入射时第1座连续梁第3跨跨中节点和第一节车车体在地震作用下的竖向加速度时程。
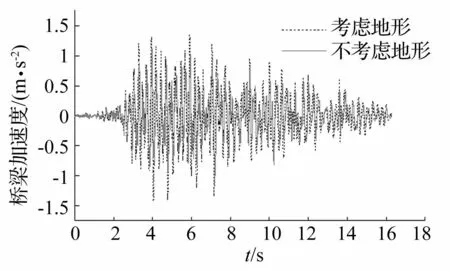
图8 桥梁竖向加速度时程 Fig.8 Vertical acceleration time history of bridge

图9 车体竖向加速度时程 Fig.9 Vertical acceleration time history of 1 st car-body
从图中可以看出,考虑地形影响后,河谷地形地震P波作用下,车桥耦合系统中桥梁子系统动力响应变大,考虑地形影响后的桥梁加速度最大值为不考虑时最大值的1.25倍左右;而车辆子系统的动力响应亦有所放大,考虑地形影响之后车体竖向加速度最大值约为不考虑时最大值的1.08倍,且峰值发生的时刻也发生了改变。
3.3河谷地形下S波入射条件下动力分析结果
如图10、图11分别为河谷地形中车速为150 km/h条件下S波入射时第1座连续梁第3跨跨中节点和第一节车车体在地震作用下的横向加速度时程。
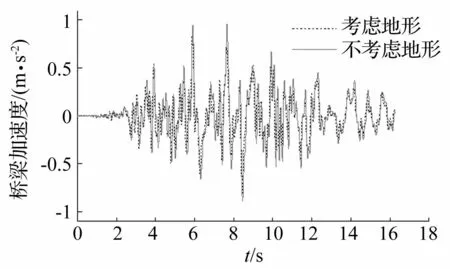
图10 桥梁横向加速度时程 Fig.10 Lateral acceleration time history of bridge

图11 车体横向加速度时程 Fig.11 Lateral acceleration time history of 1 st car-body
从图中可以看出,考虑地形条件影响后,地震S波作用下桥梁和车辆子系统的动力响应均变小,桥梁和车体横向加速度最大值分别为不考虑地形时各自最大值的0.92倍和0.80倍。从表1中可以看出,这与考虑地形条件影响后桥梁各支点横向地震动峰值较不考虑时减小有关。说明了河谷地形对地震作用下车桥耦合系统横向动力响应具有一定的有利作用。
3.4山峰地形下P波入射条件下动力分析结果
图12、图13分别给出了山峰地形中车速150 km/h条件下P波入射时第1座连续梁第3跨跨中节点和第一节车车体在地震作用下的竖向加速度时程。

图12 桥梁竖向加速度时程 Fig.12 Vertical displacement time history of bridge

图13 车体竖向加速度时程 Fig.13 Vertical acceleration time history of 1 st car body
从图中可以看出,考虑地形影响后,山峰地形地震P波作用下车桥耦合系统中桥梁子系统的动力响应变小,考虑地形影响后的桥梁加速度最大值为不考虑时的0.90倍左右;而车辆子系统的动力响应有所放大,考虑地形影响之后车体竖向加速度最大值约为不考虑时最大值的1.03倍,且峰值发生的时刻也发生了改变。
3.5山峰地形下S波入射条件下动力分析结果
如图14、图15分别为山峰地形中车速为150 km/h条件下S波入射时第1座连续梁第3跨跨中节点和第一节车车体在地震作用下的横向加速度时程。
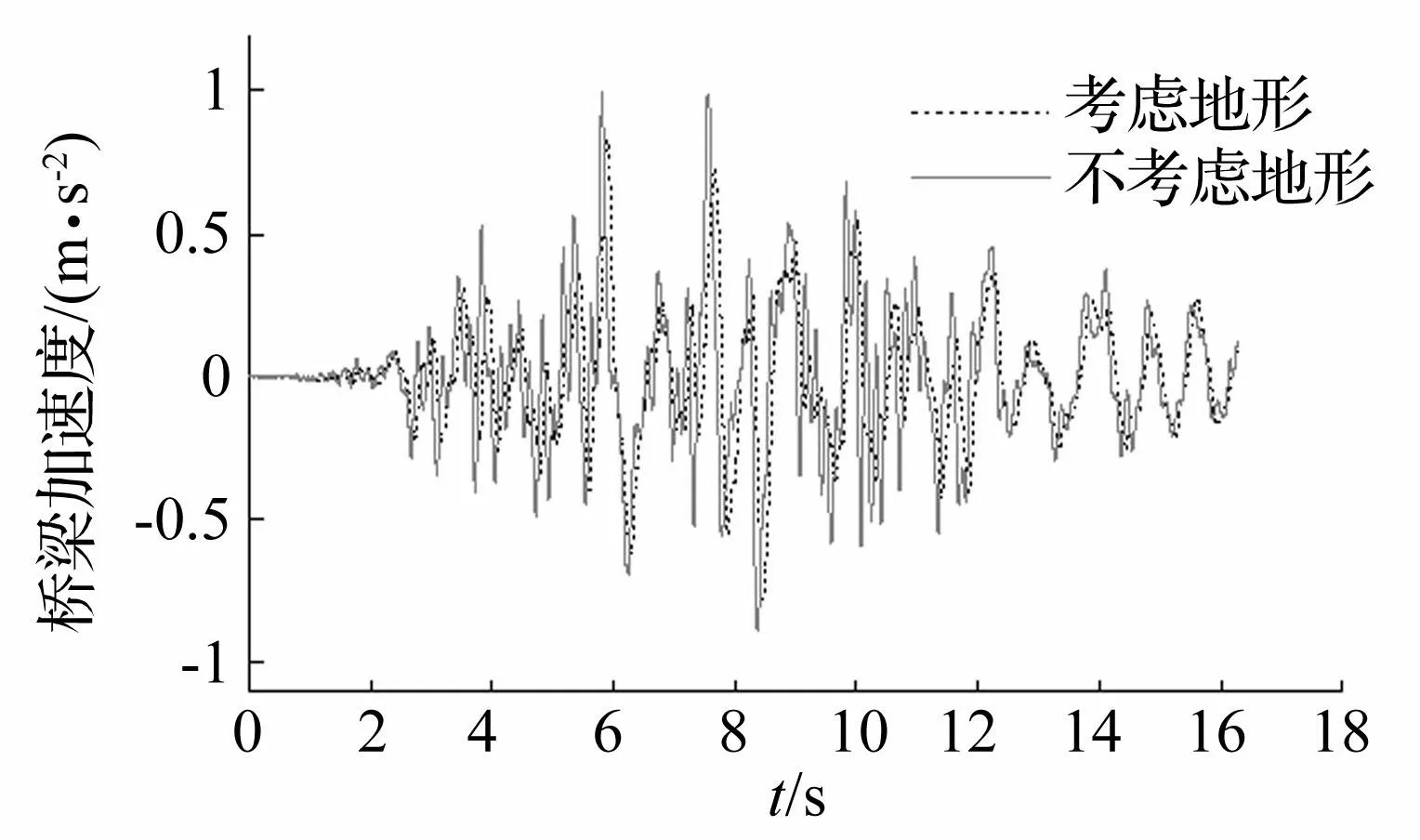
图14 桥梁横向加速度时程 Fig.14 Lateral displacement time history of bridge

图15 车体横向加速度时程 Fig.15 Lateral acceleration time history of 1 st car body
从图中可以看出,考虑地形条件影响后,山峰地形地震S波作用下桥梁的横向加速度和车体的横向加速度均有所减小,分别为不考虑地形影响时的0.83倍和0.88倍。这可能与考虑地形效应影响后,各支点在+x和-x两个方向上变化趋势不一致有关。另外,从图中可以发现,车桥系统地震响应峰值出现的时间也有一定延迟,说明局部地形既改变了车桥耦合系统地震响应的峰值大小,又改变了其峰值出现的时刻。
通过对以上算例进行初步分析,可以发现:S波入射情况下,不管是河谷地形还是山峰地形,桥梁动力响应和车辆动力响应均变小;P波入射情况下,地形条件对地震作用下车桥耦合系统动力响应的影响随着地形类型的不同而变化,河谷地形条件下,车桥耦合系统地震响应较不考虑地形条件时增大,而山峰地形条件下,桥梁地震响应减小而车体振动响应增大。
为进一步研究P波和S波入射情况下山峰地形和河谷地形对车桥耦合系统地震响应的影响,图15、16和图17、18分别给出了不同车速时,P波和S波入射情况下考虑地形影响的桥梁第1座连续梁第3跨跨中节点的竖向加速度最大值和第一节车车体竖向加速度最大值与不考虑地形影响时各自最大值的比值,简称比值。其中,车速在150 km/h ~300 km/h之间变化,每30 km/h为一个等级。

图16 P波入射时各车速下桥梁竖向加速度比值 Fig.16 Ratios of bridge vertical acceleration under different train speeds subjected to incident P wave
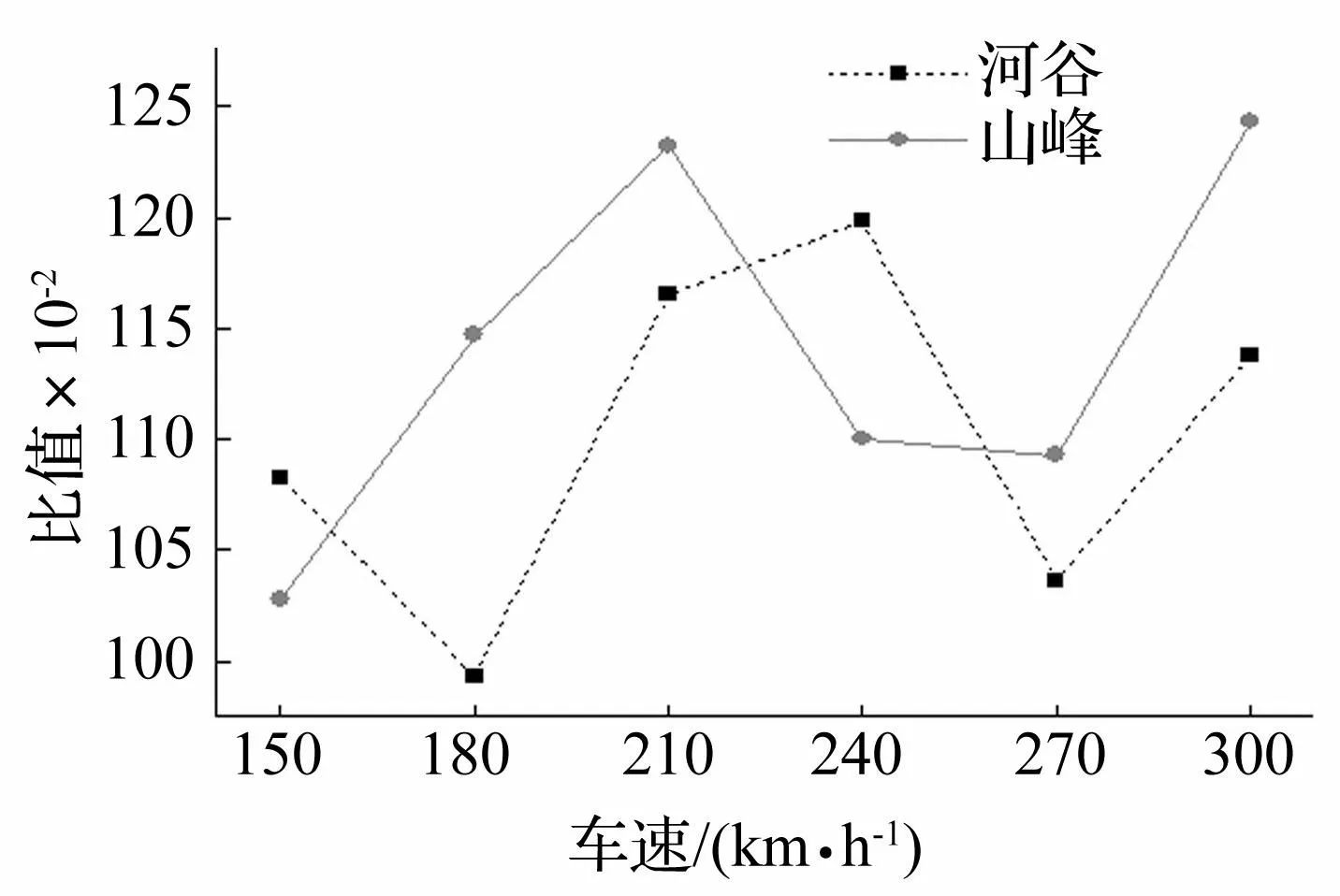
图17 P波入射时各车速下车体竖向加速度比值 Fig.17 Ratios of vehicle vertical acceleration under different train speeds subjected to incident P wave
从图16和图17中可以看出,各车速时,山峰地形下桥梁竖向加速度比值均小于1,河谷地形下桥梁竖向加速度比值均大于1,说明河谷条件对桥梁竖向振动具有放大作用而山峰地形条件对桥梁竖向振动具有减小作用;而车体竖向加速度比值则不具有以上规律,这与计算时加入了轨道不平顺有关。从图18和图19中可以看出,两种地形条件下,桥梁横向加速度在各车速时最大值均减小,但是河谷地形条件下的比值均大于山峰地形条件下的比值,说明相较于河谷地形,山峰地形对桥梁横向振动响应的影响更加明显。

图18 S波入射时各车速下桥梁横向加速度比值 Fig.18 Ratios of bridge lateral acceleration under different train speeds subjected to incident S wave

图19 S波入射时各车速下车体横向加速度比值 Fig.19 Ratios of vehicle lateral acceleration under different train speeds subjected to incident S wave
4结论
本文建立了能够反映桥梁局部场地条件的三维分析模型,编制程序计算了考虑地形影响的车桥耦合系统地震响应,并通过算例进行了初步探讨。根据计算结果,可以得到如下结论:
(1)考虑地形条件影响后,地震作用下车桥耦合系统的动力响应的峰值及其出现时间发生了变化。
(2)P波入射情况下,不管是河谷地形还是山峰地形,车辆竖向动力响应均变大,而桥梁竖向动力响应在河谷地形条件时变大,在山峰地形条件时变小。因此,在桥梁抗震设计时,应考虑地形条件的影响以保证计算结果偏于安全。
(3)S波入射情况下,不管是河谷地形还是山峰地形,桥梁和车辆的横向动力响应均变小,但产生该结果的原因不同:河谷地形条件下,车桥耦合系统地震响应减小的原因为考虑地形条件影响后,地震动输入峰值减小;山峰地形条件下,地震动输入峰值在两个方向上变化趋势不同,从而导致了加入轨道不平顺后的车桥耦合系统地震响应减小,关于这种现象产生的原因,将在以后进行深入探讨。
参考文献
[1]Xia H, Han Y, Zhang N, et al. Dynamic analysis of train-bridge system subjected to non-uniform seismic excitations [J].Earthquake Engineering and Structural Dynamics, 2006, 35: 1563-1579.
[2]Du X T, Xu Y L, Xia H. Dynamic interaction of bridge-train system under non-uniform seismic ground motion [J]. Earthquake Engineering and Structural Dynamics, 2012, 41(1): 139-157.
[3]Yang Y B, Wu Y S. Dynamic stability of trains moving over bridges shaken by earthquakes [J]. Journal of Sound and Vibration, 2002, 258(1): 65-94.
[4]谭长建, 祝兵. 地震作用下高速列车与桥梁耦合振动分析[J]. 振动与冲击, 2009, 28(1): 4-8.
TAN Chang-jian, ZHU Bing. Coupled vibration analysis of high speed train and bridge subjected to seismic excitation [J]. Journal of Vibration and Shock, 2009, 28(1): 4-8.
[5]Celibi M. Topographical and geological amplifications determined from strong-motion and aftershock records of the 3 March 1985 Chile earthquake [J]. Bulletin of the Seismological Society of America, 1987, 88(4): 1147-1167.
[6]Priestley M J N, Seible F, Calvi G M.Seismic design and retrofit of bridges [M]. New York: John Wiley & Sons Inc., 1996.
[7]Jibson R. Summary of research on the effects of topographic amplification of earthquake shaking on slope stability[R]. US Geological Survey, Open-file Report 87-268, Menlo Park, California, 1987.
[8]周国良. 河谷地形对多支撑大跨桥梁地震反应影响[D]. 哈尔滨: 中国地震局工程力学研究所, 2010.
[9]Zhou G L, Li X J, Qi X J. Seismic response analysis of continuous rigid frame bridge considering canyon topography effects under incident SV waves[J]. Earthquake Science, 2010, 23(1): 53-61.
[10]Jia H Y, Zhang D Y, Zheng S X, et al. Local site effects on a high-pier railway bridge under tridirectional spatial excitations: nonstationary stochastic analysis [J]. Soil Dynamic and Earthquake Engineering, 2013, 52: 55-69.
[11]郜新军, 赵成刚, 刘秦. 地震波斜入射下考虑局部地形影响和土结动力相互作用的多跨桥动力响应分析 [J]. 工程力学, 2011, 28(11): 237-243.
GAO Xin-jun, ZHAO Cheng-gang, LIU Qin. Seismic response analysis of multi-span viaduct considering topographic effect and soil-structure dynamic interaction based on inclined wave [J]. Engineering Mechanics, 2011,28(11):237-243.
[12]Liu J B, Du Y X, Du X L, et al. 3D Viscous-spring artificial boundary in time domain [J]. Earthquake Engineering and Engineering Vibration, 2006, 5(1): 93-102.
[13]刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998, 31(3): 55-64.
LIU Jing-bo, LÜ Yan-dong. A direct method for analysis of dynamic soil-structure interaction [J]. China Civil Engineering Journal, 1998, 31(3): 55-64.
[14]杜修力, 赵密. 基于黏弹性边界的拱坝地震反应分析方法[J]. 水利学报, 2006, 37(9):1063-1069.
DU Xiu-li, ZHAO Mi. Analysis method for seismic response of arch dams in time domain based on viscous-spring artificial boundary condition [J]. Journal of Hydraulic Engineering, 2006, 37(9):1063-1069.
[15]杜修力. 工程波动理论与方法[M]. 北京: 科学出版社, 2009.
[16]Xia H, De Roeck G, Goicolea J M. Bridge vibration and controls: New research [M]. New York: Nova Science Publishers Inc., 2011.

