基于概率密度演化的带有环形隔板圆柱形罐体中流体的晃动研究

柳　伟，周　叮，刘伟庆，王佳栋

(南京工业大学土木工程学院,南京　210009)

第一作者柳伟男，硕士，1989年生

基于概率密度演化的带有环形隔板圆柱形罐体中流体的晃动研究

柳伟，周叮，刘伟庆，王佳栋

(南京工业大学土木工程学院,南京210009)

摘要：考虑大型储油罐在地震荷载作用下罐体中流体晃动对设备造成的严重影响，工程上常采用防晃板来抑制液体的晃动，其中以环形防晃板的应用最为广泛。基于概率密度演化理论分析了带有环形隔板罐体中流体的晃动响应。首先介绍了求解罐中流体晃动响应的“流体子域法”，介绍了广义概率密度演化方程及其差分解法；然后总结了对罐中流体晃动响应进行概率密度演化分析的基本步骤；最后通过算例得出流体液面波高的均值与方差，得到波高峰值出现的时间以及最大波高峰值，这使得对流体晃动响应的把握更为精确，也为储液罐及防晃板的精细化设计提供了依据。

关键词：液体晃动响应；流体子域法；概率密度演化

基金项目：国家自然科学基金项目(11172123)

收稿日期：2014-01-02修改稿收到日期：2014-04-25

通信作者周叮男，教授，博士，1957年生

中图分类号:TB126; O323; TQ053.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.11.020

Abstract:Considering serious impacts of fluid sloshing in large-scale storage tanks under seismic loads on the devices, a baffle, especially, an annual baffle is used to control the liquid sloshing widely in practical projects. Here, the probability density evolution theory was used to analyze fluid sloshing in a cylindrical tank with an annual baffle. Firstly, the fluid sub-domain method to solve the response of fluid sloshing was introduced. Then, the basic steps of the analysis method based on the probability density evolution theory for fluid sloshing in a cylindrical tank were summarized. At last, through examples the mean and variance of the wave height of fluid surface were obtained. The appearing instants of the wave height peaks and the maximum wave height peaks were also gained. Thus, the prediction of the fluid sloshing response was more accurate. The results provided a basis for fine design of fluid storage tanks and baffles.

Sloshing response of liquid in a cylindrical tank with an annual baffle based on probability density evolution theory

LIUWei，ZHOUDing，LIUWei-qing，WANGJia-dong(College of Civil Engineering, Nanjing University of Technology, Nanjing 210009, China)

Key words:sloshing; fluid sub-domain method; probability density evolution theory

我国是一个多地震的国家，许多大型的储液罐都位于高烈度地区，抗震问题十分严峻。大型储油罐作为石油储备库的关键设备，其发展趋势是大型化，当储油罐中流体在激励作用下晃动时会对罐体造成严重破坏甚至引起倾覆，这类事故一旦发生后果不堪设想[1-3]；欲要准确地了解其性能和状态必须对结构所承受的输入以及结构系统本身有深刻的认知和把握，地震作用等作为土木工程领域的主要灾害性荷载[4-6]，因此研究地震作用下储液罐的晃动响应是相当必要的。

本文拟通过概率密度演化理论给出地震作用下储液罐体中液体晃动响应的一般规律、总结罐中流体晃动响应概率密度演化分析的一般步骤并从统计的角度给出环形防晃板在不同位置、不同尺寸时液面波高的变化情况从而为环形隔板的设计提供依据。

1罐中流体晃动响应的求解

采用王佳栋等[7]提出的流体子域法对罐中流体的晃动响应进行求解。流体子域法是在假设液体为理想流体、自由表面做微幅波动、储液罐为刚性的条件下，将有环形隔板的圆柱形储液罐中的液体分成四个子域，利用叠加法，分别求解每个子域内液体的势函数，然后将其带入子域交界面与自由表面处的边界条件确定未知系数，使问题得到解决[8-10]。

1.1流体子域法的基本方程

考虑竖向放置的带有环形隔板的圆柱型储液罐(见图1)。隔板、罐壁、罐底均为刚体，罐内部分充有无粘、无旋、不可压缩的理想流体。储液罐的内径为R1,环形隔板的外径为R2，环形隔板到自由液面和罐底的距离分别为h1、h2，忽略隔板的厚度(见图2)，将液体域分割成四个子域:i(i=1,2,3,4)。设液体子域i的速度势函数为φi(r,H,z,t),根据流体动力学的理论，柱坐标下理想流体的速度势函数应满足以下Laplace方程：

(1)

(2)

其边界条件及速度连续条件[7]如下：

(3)

(4)

(5)

(6)

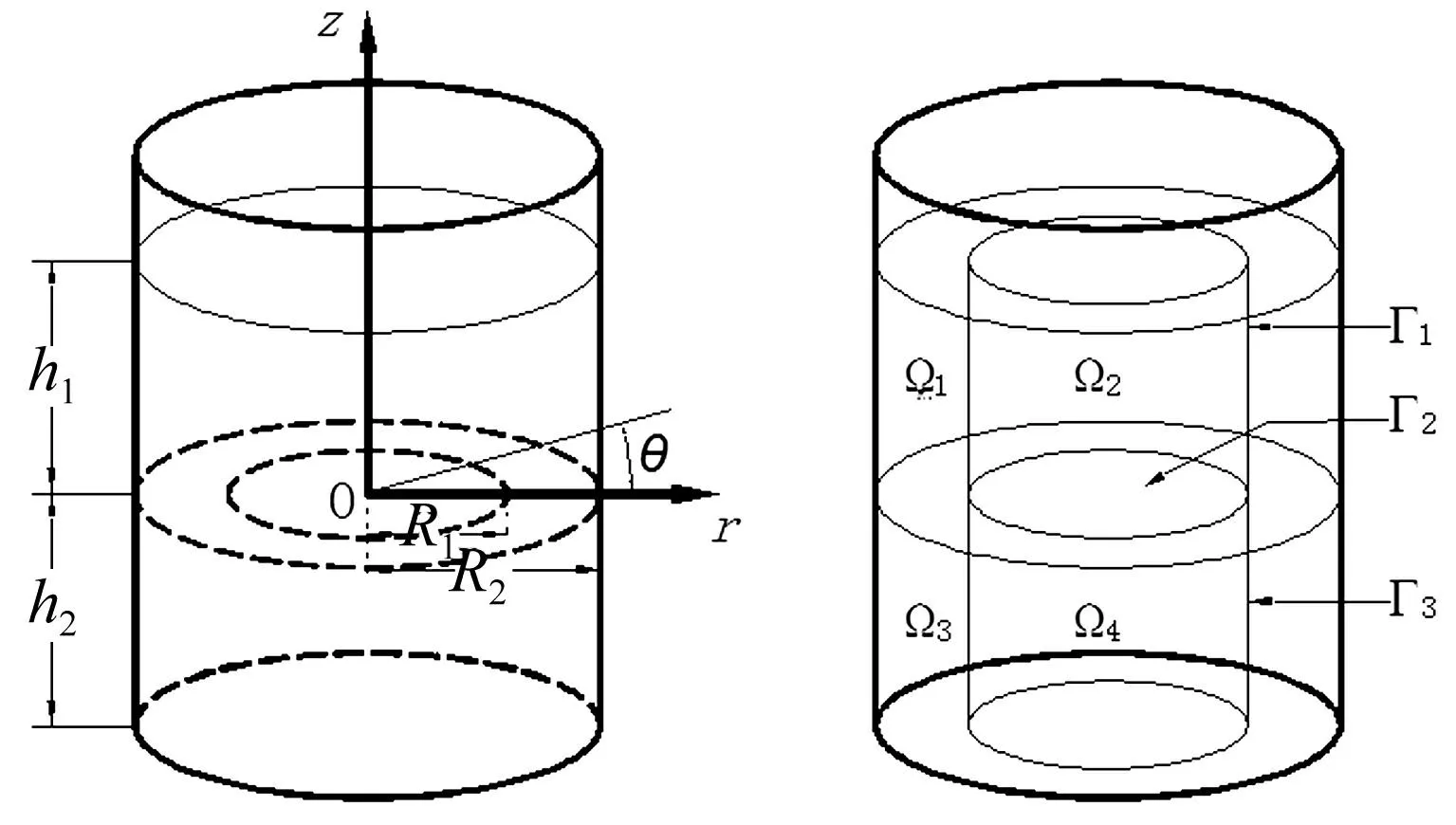
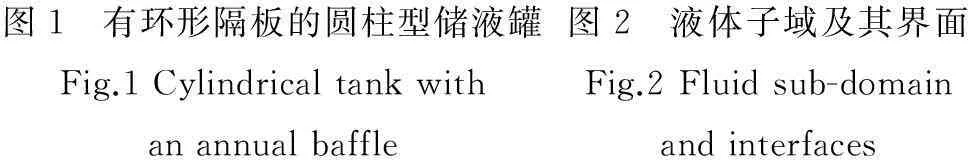
图1 有环形隔板的圆柱型储液罐Fig.1Cylindricaltankwithanannualbaffle图2 液体子域及其界面Fig.2Fluidsub-domainandinterfaces

1.2速度势函数的求解

当液面做自由波动，其液面上任一点的运动可视为简谐振动，其速度势函数也必是时间的简谐函数，可将速度势函数设为：

φi(r,θ,z,t)=jωejωtΦi(r,θ,z)

(7)

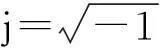
将式(7)代入基本方程及边界条件、速度连续条件可得到振型函数Φi的控制方程。该控制方程为二阶线性偏微分方程，其边界条件也均为线性，则可利用叠加原理来求解Φi。

由图2可知，液体子域可以分为两类：一类为自由表面，另一类为非自由表面。其中非自由表面又可以分为两类：与罐底平行的上下底面以及与管壁平行的圆柱面。将Φi统一写成如下形式：

(8)

式中:Φim为环向波数为m的振型函数

将Φim代入到边界条件式，得到8个含有待定系数的级数方程。对其作Fourier和Bessel展开并将所有的级数均截断至N阶，这样就可以得到关于系数Aim的矩阵方程。要使得该方程组有非零解，则系数矩阵的行列式A=0。这样就得到一个关于频率参数Λ2的非线性方程，求此方程的根就可以得到液体晃动的特征值Λ2。将各Λ2代入矩阵方程，求解方程组得到对应的Aim。

2概率密度演化理论

经典的地震动模型一般都采用功率谱密度函数表达。作为平稳过程的二阶数值特征，功率谱密度函数具有明确的统计背景，在一定程度上反映了地震动的随机特性。但是，功率谱密度函数不能刻画地震动的细部概率结构。因此研究地震动这样具有显著随机性的复杂过程更合理的方法是随机地震反应分析[12]。

一般而言，随机数据的概率密度函数建模常采用假设检验方法，即先假定随机数据服从某一分布类型，然后采用卡方检验法等检验该随机数据总体是否符合给定的分布。显然，这类方法需要对数据的概率模型有个比较准确的预判，否则会导致重复工作，更有甚者，某些数据的概率结构与常用的概率模型有着显著的差异，拟合优度检验根本不可能实现。近年来，李杰和陈建兵从概率守恒原理出发，导出了适用于随机动力系统分析的广义密度演化方程，将其与虚拟随机过程技巧相结合即可用于随机数据的概率结构建模，并在我国大陆地区年最大平均风速的处理方面获得了成功应用[13]。

2.1广义概率密度演化方程

守恒原理是连续系统的普遍规律，如质量守恒原理等。无论是概率论中随机函数的概率密度分析还是FPK方程的导出，皆蕴涵了概率守恒的基本思想。参照物理学中守恒原理的描述，概率守恒原理可以阐述为：在保守的随机系统中，系统的概率守恒。基于此原理，对于随机动力系统[13]：

(9)

可导出如下的广义概率密度演化方程：

(10)

pXΘ(x,θ,t0)=δ(x-x0)pΘ(θ)

(11)

2.2概率密度演化的数值解法

概率密度演化方程应采用数值方法求解，一般采用差分方法来求解。由于不同的差分格式其收敛和稳定性存在较大的差别，故有必要进行对比讨论，以便于不同的问题选用不同的差分格式。

(12)

将式(12)采用Taylor展开的一阶近似可以获得一阶偏微分的近似表达：

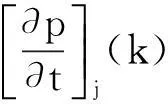
(13)

同理，对空间坐标z方向有：

(14)

将式(13)和式(14)代入式(12)：

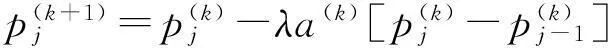
(15)

式(15)即为单边差分格式。篇幅起见，著名的L-W差分格式与TVD差分格式的推导在此不再一一赘述，具体推导过程可在文献[11-13]获得。

2.3概率密度演化的选点方法

离散代表点的选取是概率密度演化理论求解中的重要技术，建立具有理性准则的选点方法是必要的，常用的选点方法有数论选点法与切球选点法，具体方法见文献[11-13]，在此不作详述。

3流体晃动概率密度演化分析的基本步骤

储液罐中流体晃动响应的概率密度演化分析是一个复杂的系统分析过程，它集合了随机变量的选点、人工地震动的生成、储液罐中流体晃动响应的求解与地震响应的概率密度演化方程的有限差分法求解，最终得到的是储液罐中流体响应的时变均值、标准差与概率密度函数。

因此，本节基于概率密度演化理论与储液罐中流体晃动响应的特点，提出了流体晃动响应进行随机地震概率密度演化的基本分析步骤：

(1)选取离散的代表点。考虑地震动的随机性，选用基底谱幅值、场地基本圆频率以及场地等价阻尼比三个参数作为随机变量。假设这三个随机变量均服从对数正态分布。根据选点理论选取一系列离散代表点q= (1,q,2,q, …,s,q)，q=1, 2, …,nsel，nsel)为所选取离散代表点的数目，同时确定各代表点的赋得概率Pq=∫VqpΘ(θ)dθ。

(2)根据上述所选取的离散代表点，结合基于物理的地震动模型与地震动合成技术，合成多条具有概率意义的人工地震动。

(4)求解概率密度演化方程。流体晃动响应的概率密度演化方程可以写为：

q=1,2,3,……，nsel

(16)

(5)累计求和。将上述求得pX(x,θq,t)；q=1, 2, …,nsel累计求和，即得到流体波高的概率密度函数PX(x,t)的数值解。

(17)

4计算实例

采用直径为5 m，高度为5 m的圆柱形罐体进行流体晃动响应的概率密度演化分析研究，罐体中放置隔板，隔板内、外径比值分别选为R1/R2=0.1,0.5,0.9，隔板高度与水深比为h2/H=0.1,0.5,0.9。运用所给出的流体晃动相应进行随机地震概率密度演化分析的基本步骤，对该储液罐中激励方向罐壁处流体的晃动响应进行概率密度演化分析。考虑地震动的随机性，将基底幅值Sg、场地固有频率ω0和场地等价阻尼比ξ作为随机变量，随机变量的均值与变异系数按表1中Ⅱ类场地的信息进行选取。

采用样本选点法选取了202个离散代表点并确定其相应的赋得概率，根据地震动合成技术合成了202条人工地震动。图3-图4给出了人工合成地震动的两条样本。

表1　随机地震动模型参数的均值与变异系数

图3 人工合成地震动的样本W001Fig.3SynthesisofartificialgroundmotionsamplesW001图4 人工合成地震动的样本W118Fig.4SynthesisofartificialgroundmotionsamplesW118图5 W001波高响应时程Fig.5Thewaveheighttime-historyofW001

由图3～图4可知，基于随机傅里叶谱合成的人工地震动，具有显著的强度非平稳性，能很好地模拟真实的地震动记录，用于分析流体晃动随机地震响应是合理的。

基于流体子域法求解202条人工地震动下流体的晃动响应，其中由图1、图2激励所求得的罐中流体的波高响应分别见图3和图4。

采取控制变量法来分别分析不同隔板位置、不同隔板内径对流体晃动的影响。

(1)首先取隔板高度比为h2/H=0.5，隔板内径取R1/R2=0.1,0.5,0.9。分别采用L-W和TVD两种差分格式对概率密度演化方程进行求解，图7～图9分别

给出了罐中流体晃动波高的均值与标准差随时间变化的过程。从图中可知，采用两种差分格式求解的结果基本吻合，且波高的均值与标准差随时间的变化规律基本同步。

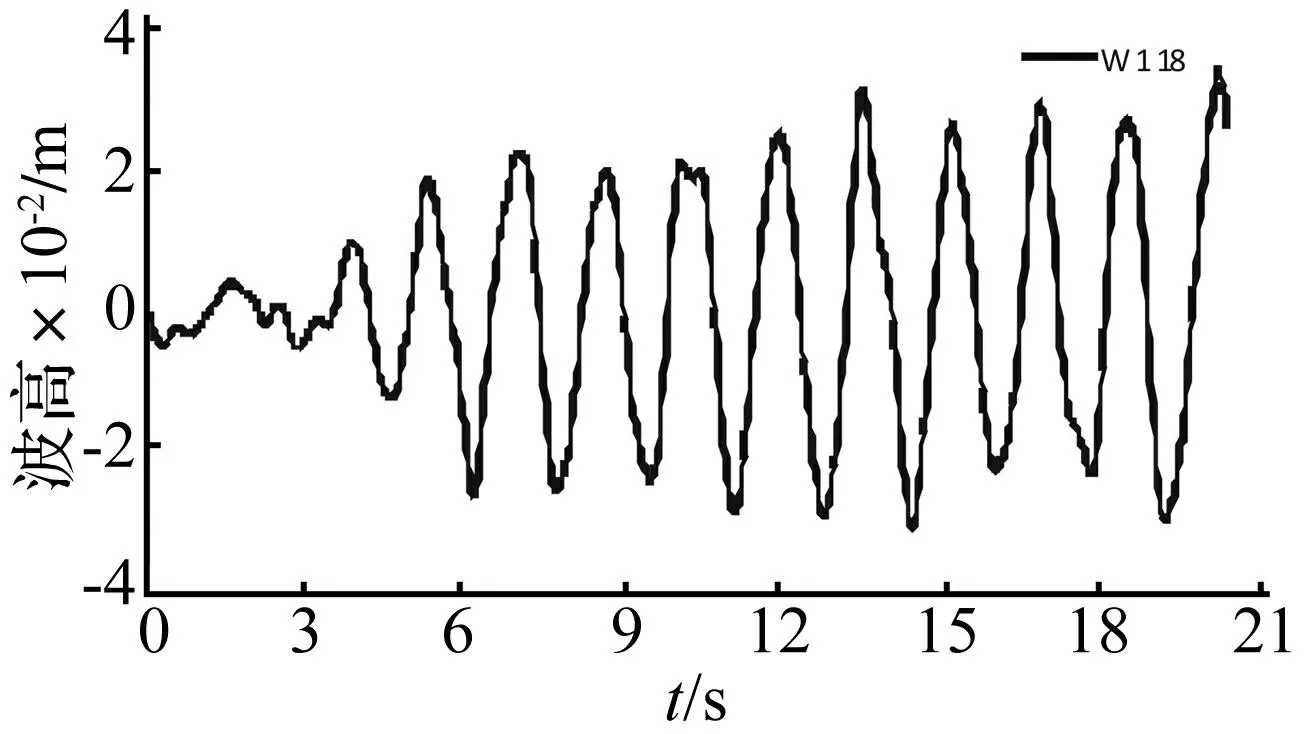
图6　W118波高响应时程Fig.6 The wave height time-history of W118

图7 p/H=0.5,R1/R2=0.9波高响应的均值和标准差Fig.7Themeanandstandarddeviationofthewaveheightp/H=0.5,R1/R2=0.9图8 p/H=0.5,R1/R2=0.5波高响应的均值和标准差Fig.8Themeanandstandarddeviationofthewaveheightp/H=0.5,R1/R2=0.5图9 p/H=0.5,R1/R2=0.1波高响应的均值和标准差Fig.9Themeanandstandarddeviationofthewaveheightp/H=0.5,R1/R2=0.1

图10 p/H=0.5,r/R=0.9波高的概率密度曲面等值线Fig.10Theprobabilitydensityevolutionofthewaveheightp/H=0.5,r/R=0.9图11 p/H=0.5,R1/R2=0.5波高的概率密度曲面等值线Fig.11Theprobabilitydensityevolutionofthewaveheightp/H=0.5,R1/R2=0.5图12 p/H=0.5,R1/R2=0.1波高的概率密度曲面等值线Fig.12Theprobabilitydensityevolutionofthewaveheightp/H=0.5,R1/R2=0.1

图10～图12分别给出了在隔板高度不变即h2/H=0.5，隔板内径与外径之比R1/R2=0.1,0.5,0.9时的波高的概率密度曲面等值线。从图中可知，内外径不同比值时最大波高出现时刻分别为12.8 s，19.8 s， 5.7 s，在各自时刻取得波高的最大值分别为0.22 m，0.19 m，0.14 m。由此可以得出结论，在带有环形隔板的圆柱形罐体中，当隔板位置不变，隔板内外径比值越小对液面波高的抑制效果越好。

(2)取隔板内外径比R1/R2=0.5,隔板高度与水深比h2/H=0.1,0.5,0.9，分别采用L-W和TVD两种差分格式对概率密度演化方程进行求解，图13～图15分别给出了罐中流体晃动波高的均值与标准差随时间变化的过程。从图中可知，采用两种差分格式求解的结果基本吻合，且波高的均值与标准差随时间的变化规律基本同步。

图13 p/H=0.1,R1/R2=0.5波高响应的均值和标准差Fig.13Themeanandstandarddeviationofthewaveheightp/H=0.1,R1/R2=0.5图14 p/H=0.5,R1/R2=0.5波高响应的均值和标准差Fig.14Themeanandstandarddeviationofthewaveheightp/H=0.5,R1/R2=0.5图15 p/H=0.9,R1/R2=0.5波高响应的均值和标准差Fig.15Themeanandstandarddeviationofthewaveheightp/H=0.9,R1/R2=0.5

图16～图18分别给出了在隔板内外径比R1/R2=0.5,隔板高度与水深比h2/H=0.1,0.5,0.9时的波高的概率密度曲面等值线。从图中可知，内外径不同比值时最大波高值出现时刻为19.8 s，6.1 s，2.2 s，在各时刻取得波高的最大值分别为0.2 m，0.15 m，0.08 m。由此我们可以得出结论，在带有环形隔板的圆柱形罐体中，当隔板内外径之比为定值，隔板离液面越近对液面波高的抑制效果越好。

图16 p/H=0.1,R1/R2=0.5波高的概率密度曲面等值线Fig.16Theprobabilitydensityevolutionofthewaveheightp/H=0.1,R1/R2=0.5图17 p/H=0.5,R1/R2=0.5波高的概率密度曲面等值线Fig.17Theprobabilitydensityevolutionofthewaveheightp/H=0.5,R1/R2=0.5图18 p/H=0.9,R1/R2=0.5波高的概率密度曲面等值线Fig.18Theprobabilitydensityevolutionofthewaveheightp/H=0.9,R1/R2=0.5

5结论

本文基于概率密度演化理论研究了环形隔板对圆柱形罐体中液面晃动响应的影响，并给出了罐体中流体波高响应进行概率密度演化分析的一般步骤。通过具体算例可以发现环形隔板对液体的晃动具有较好的抑制作用，并且抑制效果与隔板位置与隔板尺寸相关。算例中运用流体子域法求解出带环形隔板的圆柱形罐体中流体的波高响应，根据概率密度演化分析的一般步骤得到波高响应的均值与方差并求解出不同隔板位置、不同隔板尺寸下最大波高出现的时间以及波高最大值。

参考文献

[1]温德超，郑兆昌，孙焕纯.储液罐抗震研究的发展[J].力学进展，1995(1): 60-76.

WEN Zhao-de, ZHENG Zhao-chang, SUN Huan-chun. Develepment of aseismic research on liquid storage tanks[J].Advances in Mechanics,1995,(1):60-76.

[2]万水，朱德懋.横向环形防晃板对液体晃动特性的影响[J].南京航空航天大学学报，1996,41(4): 470-474.

WAN Shui, ZHU De-mao.Investigation of the effect of the ring baffle on the liquid slosh suppresion[J]. Transactions of Nanjing University of Aeronautics & Astronautics,1996,41(4):470-474.

[3]Helou A H. Dynamics of internal waves in cylindrical tank[J]. Waterway, Port, Coastal and Ocean Engineering, 1985,111(2), 453-457.

[4]欧进萍，王光远.结构随机振动[M]. 北京：高等教育出版社，1998.

[5]Soong T T,Grigoriu M. Random vibration of mechanical and structural systems [M]. New Jersey: Prentice Hall, 1993.

[6]胡聿贤.地震工程学[M]. 2版.北京：地震出版社，2006.

[7]王佳栋，周叮，刘伟庆.带环形隔板圆柱形储液罐中液体晃动的解析研究[J].振动与冲击，2010,29(3):54-59.

WANG Jia-dong,ZHOU Ding,LIU Wei-qing. Analytical solution for liquid sloshing with small amplitude in a cylindrical tank with an annual baffle[J].Jounal of Vibraraion and Shock,2010,29(3):54-59.

[8]王佳栋，周叮，刘伟庆.水平激励下带环形刚性隔板圆柱形储液罐中流体的晃动响应[J].力学季刊，2011,32(2):166-172.

WANG Jia-dong, ZHOU Ding, LIU Wei-qing. Sloshing response of liquid in cylindrical tank with a rigid annual baffle under horizontal loads[J].Chinese Quarterly of Mechanics,2011,32(2):166-172.

[9]Biswal K C, Bhattacharyya S K, Sinha P K. Dynamic response analysis of a liquid-filled cylindrical tank with annular baffle [J]. Journal of Sound and Vibration, 2004, 274(1/2):13-37.

[10]Zhou D, Liu W Q. Hydro-elastic vibrations of flexible rectangular tanks partially filled with liquid [J]. International Journal for Numerical Methods in Engineering, 2007,71: 149-174.

[11]李杰，陈建兵. 随机振动理论与应用新进展[M].上海:同济大学出版社，2009.

[12]李杰，陈建兵，张琳琳,等. 中国大陆地区年最大平均风速的概率密度函数[J]. 自然灾害学报，2006,15(5): 76-82.

LI Jie,CHEN Jian-bing, ZHANG Lin-lin.Probability density function of yearly maximum average wind speed in mainland of chian[J].Jounal of Natural Disasters,2006,15(5):76-82.

[13]李杰，陈建兵. 随机动力系统中的广义密度演化方程[J]. 自然科学进展，2006,16(6): 712-719.

LI Jie,CHEN Jian-bing, Generalized density evolution equation in a random dynamical system[J].Progress in Natrue Science,2006,16(6):712-719.