考虑齿轮-转子系统振动响应的最佳修形曲线研究

马　辉，逄　旭，宋溶泽，闻邦椿

(东北大学机械工程与自动化学院，沈阳　110819)

第一作者马辉男，博士，副教授，1978年生

考虑齿轮-转子系统振动响应的最佳修形曲线研究

马辉，逄旭，宋溶泽，闻邦椿

(东北大学机械工程与自动化学院，沈阳110819)

摘要：轮齿修形可减小齿轮静态传动误差，改善齿轮动态特性。基于现有文献，考虑基圆与齿根圆不重合，在齿廓精确建模的基础上确定齿轮的时变啮合刚度和静态传动误差。针对不同修形曲线在不同修形量下齿轮静态传动误差的变化进行分析，给出了不同修形量范围内的最佳修形曲线，并结合齿轮-转子系统动力学模型，考虑齿廓修形引起的无载荷静态传动误差，分析不同修形曲线下系统的振动特性，进一步确定不同转速下最佳修形曲线。研究结果表明通过评估齿轮-转子系统的振动特性，可更好地确定不同转速下的轮齿的最佳修形曲线。

关键词：齿廓修形；时变啮合刚度；静态传动误差；齿轮-转子系统；振动响应

基金项目：中央高校基本科研业务费专项资金资助(N130403006);教育部新世纪人才支持计划(NCET-11-0078)

收稿日期：2014-01-08修改稿收到日期：2014-05-07

中图分类号:TH113

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.11.004

Abstract:Tooth profile modification can decrease the loaded static transmission error, and improve the dynamic characteristics of gear pairs. Here, based on available theories and literatures, the time-varying mesh stiffness (TVMS) and static transmission error (STE) were determined with a correction method considering misalign effect between the root circle and tooth base circle and an accurate gear profile curve. The optimal profile modification curves with different amounts of profile modification were determined by analyzing the STE changing with different profile modification curves and different amounts of profile modification. Combining a gear-rotor system dynamic model and considering the effect of no-load STE caused by profile modification, the vibration responses of the gear-rotor system with different gear profile modification curves were analyzed to determine the optimal profile modification curves at different rotating speeds. The results showed that the optimal gear profile modification curves at different rotating speeds can be determined by evaluating the vibration responses of the gear-rotor system.

Optimal profile modification curves for spur gears considering vibration responses of a gear-rotor system

MAHui,PANGXu,SONGRong-ze,WENBang-chun(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Key words:profile modification; time-varying mesh stiffness; static transmission error; gear-rotor system; vibration response

受制造、安装误差、齿轮弹性变形及热变形等的影响，齿轮啮合时不可避免地产生冲击、振动和偏载，导致齿轮早期失效的概率增大。生产实践和理论表明，适当的轮齿修形，对改善齿轮运转性能、提高承载能力、延长使用寿命有明显的效果[1]。

许多学者对齿廓修形问题进行了研究，通过建立齿轮三维有限元模型，Ohno等[2]分析了接触压力和斜齿轮修形量的关系，确定了斜齿轮的最佳修形量。基于非线性接触理论，Wagaj等[3]建立二维、三维斜齿轮副接触有限元模型，分析了直线、抛物线齿顶修形以及齿向修形对斜齿轮静态传动误差的影响。Li[4]使用有限元法研究了加工误差、装配误差和齿向修形对直齿轮轮齿表面接触应力、齿根弯曲应力、载荷分布和静态传动误差的影响。通过建立的直齿轮副有限元模型，Tharmakulasingam等[5]研究发现齿廓修形能降低齿顶、齿根应力以及静态传动误差的幅值，并且静态传动误差会随着扭矩增大而增大。Tesfahunegn等[6]采用非线性有限元方法分析齿形修整对传动误差、接触压力以及齿根应力的影响。Tavakoli等[7]对直线修形和曲线修形下的静态传动误差进行了频率分析，表明传动误差变化越平滑，波动幅值越小，齿轮传动越平稳。Ma等[8]通过Ansys软件建立了齿顶修缘的直齿轮啮合有限元模型，主要研究了齿顶渐开线修缘对齿轮-转子系统振动响应的影响。Chen等通过建立解析模型，研究了齿廓修形、扭矩及齿根裂纹对齿轮啮合刚度、负载分配及有载荷静态传动误差的影响。

从现有的文献来看，针对齿廓修形，大多关注于载荷分布，静态传动误差及齿轮副的振动特性，对于最佳修形曲线的确定，也仅限于修形量一定的情况。本文基于Chen等[9]建立的解析模型，获得齿轮时变啮合刚度和静态传动误差，分析了不同修形量范围内的最佳修形曲线，并结合齿轮-转子系统模型，在考虑无载荷静态传动误差的条件下，通过齿轮-转子系统在不同修形曲线下的振动特性来验证最佳修形的有效性，分析流程见图1。

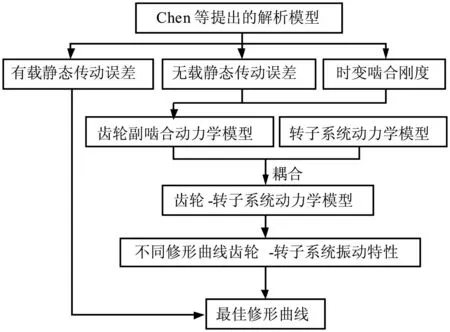
图1　分析流程图Fig.1 Flow chart of analysis

1考虑修形的轮齿啮合刚度及静态传动误差确定

1.1修形方法

齿廓修形有三种方式，齿顶修缘、齿根修缘及全齿廓修缘(齿顶和齿根同时修缘)，齿廓修形的设计包括确定修形长度、修形量和修形曲线。对轮齿进行齿根修缘，可以相当于对与之配对的轮齿进行齿顶修缘，因此齿顶修缘、齿根修缘及全齿廓修缘可达到同样的修形效果，本文采用齿顶修缘(见图2)。修形量用参数Cn表示，Cn=Ca/Ca_max，Ca为齿顶修形量，最大齿顶修形量Ca_max=0.02m，m为齿轮模数，修形长度用ΔLn表示，ΔLn=ΔLa/ΔLa_max,ΔLa为沿啮合线方向的修形长度，ΔLa_max=0.6m。修形曲线方程一般为[10]

(1)

式中:x为以修形起点为坐标原点时啮合线上任一位置的坐标，C为位置x处的修形量。本文选取三种修形曲线：n=1.5，n=2和渐开线，考虑齿顶修形方式，且修形长度ΔLa取各轮齿单双齿啮合区单侧长度进行分析，确定不同修形量范围内的最优修形曲线。

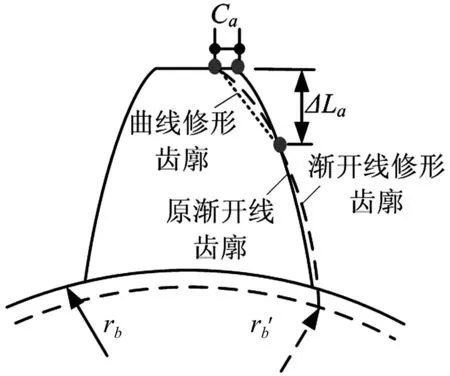
图2　齿廓修形示意图Fig.2 Schematic of gear tooth profile modification

1.2考虑修形的时变啮合刚度和传动误差确定

齿轮参数见表1，假设扭矩T1=150 N·m，主动轮和从动轮的修形长度分别为各轮齿单双齿啮合区单侧长度ΔLa1=1.595 mm，ΔLa2=1.546 mm，即ΔLn1=1.519，ΔLn2=1.472，在Chen等提出的解析模型基础上，考虑基圆与齿根圆不重合[11]及真实过渡曲线[12]，针对表2所示的三种仿真工况，得到的三种工况下的时变啮合刚度、有载荷和无载静态传动误差(见图3)。

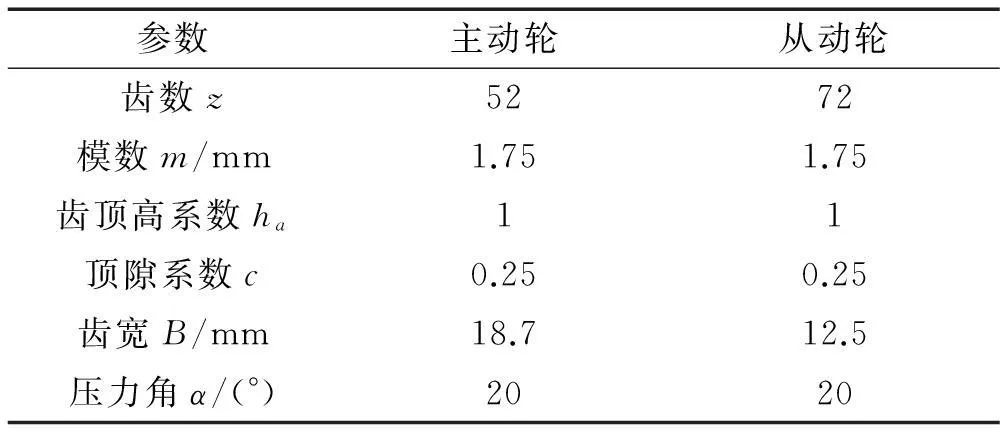
表1　齿轮几何参数

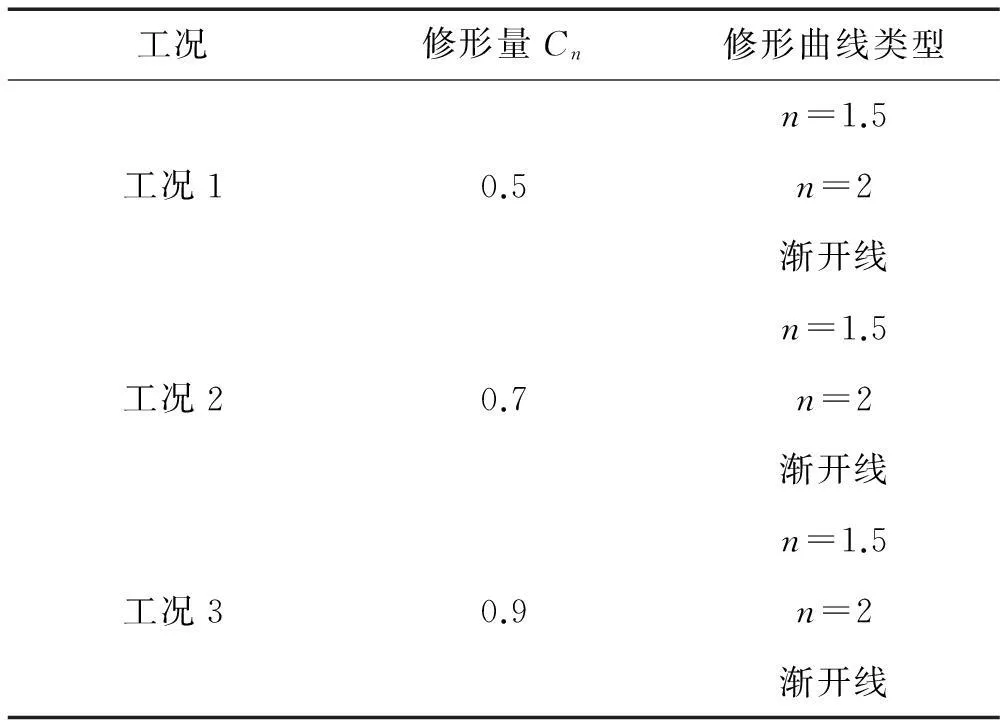
表2　仿真工况

由图3可知，相同修形量的情况下3种修形方法对应的齿轮时变啮合刚度几乎完全相同，但有载荷静态传动误差有所不同；采用同一修形方法不同修形量进行齿顶修形时，齿轮的重合度随着修形量的增大而减小，有载荷静态传动误差也有明显的变化。由此可见，通过适当的修形可以降低有载荷静态传动误差的波动。

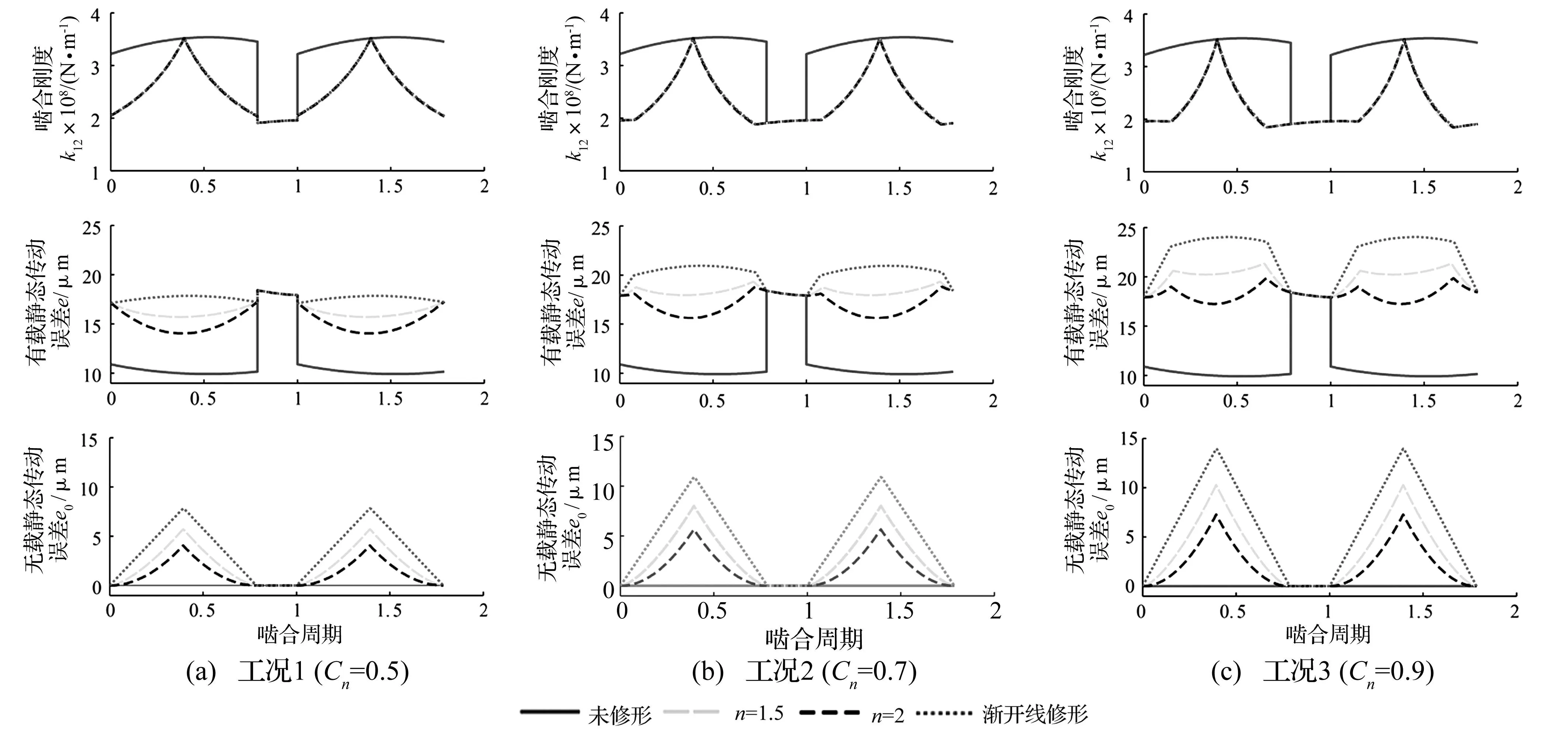
图3　三种工况下的时变啮合刚度和静态传动误差Fig.3 TVMS and STE under three conditions

1.3不同修形方法下的最佳修形确定

静态传动误差变化的相对峰峰值可用r来衡量，其表达式如下：

(2)

式中:pn和pm为未修形和修形情况下的有载荷静态传动误差峰峰值。有载荷静态传动误差变化幅度越小，即相对峰峰值r越小，修形效果越好。三种修形曲线，有载荷静态传动误差相对峰峰值r随修形量Cn的变化情况，见图4，A、B两点将修形量区间分为3部分，在区间[0,0.608]内，相同修形量下，渐开线修形获得的有载荷静态传动误差相对峰峰值r变化最小，修形效果最佳；在区间[0.608,0.837]内，曲线n=1.5的修形效果最佳；当Cn大于0.837时，曲线n=2的修形效果最佳。因此在修形量确定的情况下，可根据该图选择修形曲线，以达到最佳修形效果，但值得注意的是修形量Cn过大，重合度会降低过多，会导致齿轮运转平稳性降低，引起振动和噪声，反而达不到修形的作用。因此应根据实际情况，确定适当的修形量，进而选择最佳修形曲线进行修形。

图4　不同修形量下的有载荷静态传动误差相对峰峰值Fig.4 Relative peak-peak value of loaded STE under different amounts of profile modification

2考虑齿轮-转子系统振动特性的最佳修形

仅利用有载荷静态传动误差相对变化来确定最佳修形曲线，不能反映修形对齿轮动态特性的影响，此外利用齿轮-转子系统的动态响应来反映系统的振动特性更具现实意义，因此本节将采用修形后齿轮-转子系统的振动特性，来验证最佳修形曲线的选取。

2.1齿轮-转子系统模型建立

将齿轮视为通过弹簧和阻尼器连接的刚性圆盘，其啮合动力学模型见图5，O1，O2为齿轮中心，Ω1、Ω2为齿轮转动角速度，取逆时针为正，顺时针为负；rb1、rb2为齿轮基圆半径；齿轮时变啮合刚度和阻尼分别用k12(t)和c12(t)(本文c12(t)=0)表示；定义y轴正向与啮合面的夹角为：

(3)

式中:α为齿轮压力角，α12(0≤α12≤ 2π)为主动轮的x轴逆时针旋转至中心线的夹角。

为了考虑主动轮转动方向的影响，引入σ函数：

(4)

设两齿轮在啮合线方向上的相对位移为p12(t)，则

p12(t)=(-x1sinψ12+x2sinψ12+y1cosψ12-

y2cosψ12+σ×rb1θz1+σ×rb2θz2)-e12(t)

(5)

式中:e12(t)为静态传动误差，本文仅考虑由于修形引起的齿廓误差，即无载荷静态传动误差e0(t)。

图5　齿轮副啮合动力学模型Fig.5 Dynamic model of gear pair

不考虑齿侧间隙、啮合摩擦力等的影响，分别建立齿轮在六个自由度方向的运动方程：

式中:m1、m2为齿轮1、齿轮2的质量，Ix1、Iy1、Iz1、Ix2、Iy2、Iz2分别为齿轮1和齿轮2绕x轴、y轴和z轴的转动惯量，T1为施加在主动轮扭矩，T2为负载扭矩。

将其简化成矩阵形式，得到齿轮副运动耦合方程为：

(7)

式中:X12为齿轮副质心的广义坐标，M12为齿轮副的质量矩阵，K12为啮合刚度矩阵，C12为啮合阻尼矩阵，G12为陀螺矩阵。

将齿轮啮合动力学模型和转子系统模型进行耦合，得到如图6所示的齿轮-转子系统有限元模型。系统的运动方程可表示为：

(8)

式中:M为系统质量矩阵，包含转轴质量、齿轮质量以及集中质量；G为陀螺力矩；C为系统阻尼矩阵，采用粘性阻尼；K为系统刚度矩阵，包括转轴刚度、齿轮啮合刚度以及轴承刚度。u为系统广义坐标，Fu为激振力矢量。

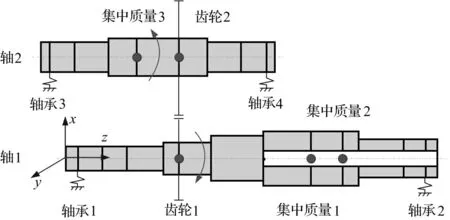
图6　齿轮-转子系统有限元模型Fig.6 Finite element model of a gear-rotor system

2.2考虑不同轮齿修形的系统振动特性分析

本节将分析表2所示的3种工况下齿轮-转子系统的振动响应。工况1 (Cn=0.5)齿轮1处x方向位移和齿轮啮合力均方根随啮合频率的变化曲线见图7，由图7(a)可知，未修形时，当啮合频率ω12分别等于系统的固有频率ω1、ω3、ω7、ω9，ω1/n(n=6,5,4,3,2)和ω7/2时位移响应出现共振峰，修形后ω7/2处的共振峰消失，并且位移响应幅值明显降低。当啮合频率大于150 Hz时，位移响应均方根值由大到小依次为未修形、曲线n=2修形、曲线n=1.5修形和渐开线修形，即渐开线修形效果最佳，与图4中修形量Cn=0.5时静态传动误差相对峰峰值大小顺序所对应修形曲线一致，说明了静态传动误差相对峰峰值越小，修形效果越好；当啮合频率低于150 Hz时，在啮合频率等于ω1/3处，曲线n=2修形对应的幅值最低；在啮合频率等于ω1/4处，曲线n=1.5修形对应的幅值最低。因此，啮合频率较低时，仅根据有载荷静态传动误差选取最佳修形曲线是不够的，需根据齿轮的工作转速，结合齿轮振动特性选取修形曲线。由图7(b)可知，修形后啮合力幅值显著降低，并且渐开线修形对应的啮合力变化最为平缓。

图7　齿轮1处x方向位移和啮合力均方根变化曲线(Cn=0.5)Fig.7 Root-mean-square of displacement in the xdirection of gear 1 and gear mesh force (Cn=0.5)

齿轮1处x方向振动加速度随时间变化曲线见图8，从图中可以看出修形后齿轮的振动加速度幅值显著降低。

当啮合频率高于2 600 Hz时，振动响应的变化十分平缓(图7)，因而对于工况2和工况3只分析转速在0～2 600 Hz范围内的振动特性。图9为工况2 (Cn=0.7)齿轮1处x方向位移均方根值随啮合频率的变化曲线，啮合频率较高时，n=1.5修形曲线修形效果最佳，而渐开线和n=2修形曲线的修形效果几乎相同，规律与图4有载荷静态传动误差相对峰峰值变化规律相同；啮合频率较低时，渐开线修形效果最差。图10为工况3 (Cn=0.9)齿轮1处x方向位移均方根值随啮合频率的变化曲线，啮合频率较高时，n=2修形曲线修形效果最佳，其次是n=1.5修形曲线，渐开线修形效果最差，规律与图4有载荷静态传动误差相对峰峰值变化规律相同；啮合频率较低时，渐开线修形效果仍为最差。

图8 齿轮1处x方向加速度响应曲线(Cn=0.5)Fig.8Accelerationresponsesofgear1inxdirection(Cn=0.5)图9 齿轮1处x方向位移均方根值(Cn=0.7)Fig.9Root-mean-squareofdisplacementinthexdirectionofgear1(Cn=0.7)图10 齿轮1处x方向位移均方根值(Cn=0.9)Fig.10Root-mean-squareofdisplacementinthexdirectionofgear1(Cn=0.9)

3结论

(1)由于齿轮有载荷静态传动误差峰峰值相对变化越小，修形效果越好，本文通过对比三种修形曲线在不同修形量下对应有载荷静态传动误差峰峰值，获得了不同修形量对应的最佳修形曲线。

(2)由于有载荷静态传动误差不能反映齿轮的动态特性，本文通过齿轮-转子系统的动态特性进一步确定最佳修形曲线，发现高频情况下通过齿轮-转子系统动态特性确定的最佳修形曲线与根据有载荷静态传动误差峰峰值确定的最佳修形曲线相同，但在低频情况下，二者有所差别。根据扭矩、修形曲线、修形长度，可获得不同修形量下有载荷静态传动误差峰峰值，高频时可通过比较有载荷静态传动误差峰峰值确定最佳修形曲线，低频时需根据齿轮-转子系统振动特性确定最佳修形曲线。

参考文献

[1]朱孝录．齿轮传动设计手册[M]．北京：化学工业出版社，2005．

[2]Ohno K，Tanaka N．Contact stress analysis for helical gear with 3-dimensional finite element method[J]．Transactions of the Japan Society of Mechanical Engineers．C，1998，64：4821-4826．

[3]Wagaj P，Kahraman A．Impact of tooth profile modification on the transmission error excitation of helical gear pairs[C]．Proceedings of ESDA2002：6th Biennial Conference on Engineering Systems Design and Analysis， Istanbul，Turkey，2002:8-11．

[4]Li S T．Effects of machining errors，assembly errors and tooth modifications on loading capacity, load-sharing ratio and transmission error of a pair of spur gears[J]．Mechanism and Machine Theory，2007，42(6)：698-726．

[5]Tharmakulasingam R，Alfano G， Atherton M．Reduction of gear pair transmission error with tooth profile modification[C]．ISMA 2008, International Conference on Noise and Vibration Engineering，Leuven，Belgium，2008:15-19．

[6]Tesfahunegn Y A，Rosa F，Gorla C．The effects of the shape of tooth profile modification on the transmission error，bending，and contact stress of spur gears[J]．Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2010，224(8)：1749-1758．

[7]Tavakoli M S，Houser D R．Optimum profile modifications for the minimization of static transmission errors of spur gears[J]．ASME Journal of Mechanism, Transmissions and Automation in Design，1986，108(3)： 86-95．

[8]Ma H, Yang J, Song R Z, et al. Effects of tip relief on vibration responses of a geared rotor system, proceedings of the institution of mechanical engineers, part c[J].Journal of Mechanical Engineering Science，2014，228(7)：1132-1154.

[9]Chen Z G，Shao Y M．Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]．Mechanism and Machine Theory，2013，62：63-74．

[10]李润方，王建军．齿轮系统动力学-振动、冲击、噪声[M]．北京：科学出版社，1997．

[11]万志国，訾艳阳，曹宏瑞，等．时变啮合刚度算法修正与齿根裂纹动力学建模[J]．机械工程学报，2013, 49(11)：153-160．

WAN Zhi-guo，ZI Yan-yang，CAO Hong-rui，et al．Time-varying mesh stiffness algorithm correction and tooth crack dynamic modeling[J]．Journal of Mechanical Engineering，2013，49(11)：153-160．

[12]郭忠，张艳冬．基于APDL的渐开线直齿圆柱齿轮参数化精确建模[J]．机械制造与研究，2010，39(3)：33-36．

GUO Zhong，ZHANG Yan-dong．Parameterization precise modeling of involutes spur gear based on APDL [J]．Machinery Manufacturing and Research，2010，39(3)：33-36．