改进型FULMS算法实现压电机敏框架结构振动抑制

黄全振,朱晓锦,高志远,高守玮

(1. 上海大学机电工程与自动化学院,上海　200072; 2. 河南工程学院电气信息工程学院,郑州　451191)

第一作者黄全振男，博士，讲师，1979年生

改进型FULMS算法实现压电机敏框架结构振动抑制

黄全振1,2,朱晓锦1,高志远1,高守玮1

(1. 上海大学机电工程与自动化学院,上海200072; 2. 河南工程学院电气信息工程学院,郑州451191)

摘要：航空航天器结构振动主动控制研究一直非常活跃，其中自适应滤波FULMS算法构成主要控制方法之一，但该算法存在一个如何提取有效参考信号的问题。提出一种改进型FULMS振动控制算法，算法过程是通过从振动结构中直接提取振动响应残差信号，进而基于控制器结构和算法过程数据构造出参考信号，满足于激扰信号的相关性并进入算法控制过程；在此基础上，构建了一种压电机敏框架结构和实验平台进行实验验证，阐述了实验模型结构模态分析、分布式压电传感器和驱动器优化配置，以及实验平台构建和实验过程分析。研究结果表明，改进型FULMS算法较为有效地解决了参考信号实际获取问题，并具有良好的收敛性和结构振动抑制效果，对自适应滤波振动控制算法进一步实用化具有良好意义。

关键词：压电机敏结构；振动主动控制；自适应滤波控制；参考信号；滤波-U算法

基金项目：国家自然科学基金资助项目(90716027；61305106);中国博士后科学基金资助项目(2013M541505)

收稿日期：2014-01-20修改稿收到日期：2014-05-08

通信作者朱晓锦男，博士，教授,博士生导师，1965年生

中图分类号:TB535; TP13; V414

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.11.005

Abstract:Active vibration control of aerospace vehicles is a hot topic. The daptive filtered-U least mean square (FULMS) algorithm is a main control algorithm. But vibration reference signal extraction is always a difficult problem for FULMS algorithm. Here, through picking vibration response residual signals, an improved FULMS algorithm was proposed to construct the reference signal related to external disturbance signal based on the controller structure and the algorithm process data. A test platform was constructed to test a piezoelectric smart aircraft framework structure. Its modal analysis was done, piezoelectric sensors and actuators were ployed optimally. The simulation and test results showed that the proposed algorithm can be used to solve the reference signal extraction problem and it has a good convergent speed and a good vibration suppression performance; it is of significance for adaptive filtering vibration control to be realized.

Vibration suppression of a piezoelectric smart framework structure based on improved FULMS algorithm

HUANGQuan-zhen1,2,ZHUXiao-jin1,GAOZhi-yuan1,GAOShou-wei1(1. School of Mechatronics Engineering and Automation, Shanghai University, Shanghai 200072, China;2. School of Electrical Information Engineering, Henan Institute of Engineering, Zhengzhou 451191, China)

Key words:piezoelectric smart structures; active vibration control; adaptive filtering control; reference signal; filtered-U algorithm

临近空间飞行器具有当今世界作战飞机和地空导弹均无法达到其飞行高度的优势，同时制造和应用成本相比卫星、航天飞机低得多等特点，目前许多航空发达国家正在积极开展其研究工作，但大多数国家基本仍处于概念研究和可行性试验阶段；虽然我国在该领域的研究起步较晚，但它关系到国家安全战略与和平利用空间的重大问题，近年来国家予以高度关注与重视[1-2]，尤其针对相关重要基础科学问题的研究，如结构控制中的振动控制问题[3]。

当前基于压电机敏结构概念实现飞行器结构振动控制是一个重要研究方向，即通过将压电传感器、压电驱动器和控制器有机地与基体结构集成在一起，通过适当的控制方法和控制策略，使得驱动器的控制输出产生准确的动作以改变结构的特性与状态，从而达到自适应实现结构振动控制的目的，其中控制器设计及其自适应控制算法是核心问题之一。Hidebrand等[4-5]已做了大量的研究，并提出了一些有效的控制算法，但很多算法仅获得了初步实现，发展并不成熟。如Huang等[6]分别利用分散化控制和集中控制方法对飞行器柔性附件振动进行了研究；段丽玮等[7]运用H∞鲁棒控制理论的混合灵敏度方法对飞行器尾翼进行振动控制研究；此外，具有控制修正速率高、对非平稳响应适应能力强的自适应滤波控制算法在振动主动控制领域获得广泛关注，其中较为典型的FULMS (Filtered-U Least Mean Square)控制[8]算法研究获得较多关注，如Kin等[9]提出了带超稳定自适应递归滤波器的变步长的MFU-LMS算法，Cheng等[10]提出了基于人工神经网络自适应滤波器的NFURLMS算法，有效提高了FULMS控制算法的控制效果。但该控制算法存在一个明显的缺陷：它需要预知与外激扰信号相关的参考信号，而在真正的航天器在轨运行过程中，一般很难或无法预知参考信号；为了弥补这一不足，相关研究者提出通过安装参考信号传感器于飞行器结构以获得参考信号，然而结构化的传感装置一方面可能难于安装在飞行器实际结构中，另一方面由于实际飞行环境的复杂性和突变性，有可能参考传感器所采集的信号并不准确，这样导致整个控制系统无法实现有效控制。

本文以临近空间飞行器结构振动控制为研究背景，设计了一种模拟飞行器框架结构的压电机敏模型结构，并以压电陶瓷元件作为传感器和驱动器分布式植入结构表面，通过配置相关测控系统构成结构振动主动控制实验平台；在分析FULMS算法结构的基础上，针对参考信号难以事先预知的问题，提出一种新型的FULMS振动控制算法，并基于模型结构和实验平台进行振动抑制验证。具体方法是通过从振动结构中直接提取振动响应残差信号，进而基于控制器结构和算法过程数据构造出参考信号，满足于激扰信号的相关性并进入算法控制过程，并通过仿真分析和实验验证；研究结果表明，本文所提控制算法具有可行性和有效性。

1常规多通道模式FULMS控制算法

FULMS算法是以无限脉冲响应(Infinite Impulse Response, IIR)滤波器结构所构成的滤波U最小均方差算法，IIR滤波器由于其本身自有的零-极点结构，能以较低阶数实现受控系统的控制器建模，因此面对结构振动主动控制器设计，使用基于IIR滤波器结构的自适应振动控制算法能够节省较多计算量。FULMS算法结构见图1。

图1　FULMS算法结构图Fig.1 Structure diagram of FULMS algorithm

(1)

wp(k),d0(k),d1(k),…,dq(k)]T

U(k)=[x(k),…,x(k-p),y(k-1),…,y(k-q)]T

式中:p和q为延迟量。

MIMO控制方式的IIR模式控制器自适应控制过程，实际上就是寻求最优的W*与D*过程，通过M个控制器输出控制信号于M个作动器，最终使受控结构L个测点处的误差响应信号的均方值之和为最小；依据最陡下降法可推导得到基于LMS准则的寻求最佳权值递推公式。适用于结构振动MIMO控制方式的FULMS算法[11]大致归纳为：

(2)

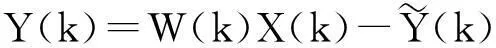
(3)

(4)

(5)

式(4)、式(5)中，μ、α的取值范围分别为0<μ<1/λmax，0<α<1/λmax，其中λmax是参考信号自相关矩阵的最大特征值。μ、α的值是根据输入信号的自相关矩阵的特征值来选取的，要求保证算法收敛并保持较快的收敛速度，因此最优值一般可通过试探方式予以确定。

2改进型FULMS控制算法

B(k)=E(k)+H2(z)Y(k)

(6)

(7)

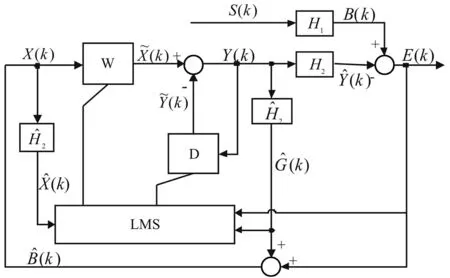
图2　改进型FULMS算法结构图Fig.2 Structure diagram of improved FULMS algorithm

经过类似于文献[11]所述的FULMS算法的推理过程，其控制算法大致可以概括为：

(8)

(9)

(10)

(11)

(12)

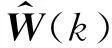
其中，p和q为延迟量。

3压电机敏框架与实验平台构建

3.1框架模型结构模态分析

为了便于验证本文所提控制算法，对模拟临近空间飞行器模型结构尽量简化，最终将其简化为一个铝合金框架结构，并在框架四个边角施加弹簧约束，见图3。

图3　简化后的框架模型结构Fig.3 Simplified model of aircraft framework

框架结构主要有铝合金板材和用于连接的弹簧组成，铝合金板材主要性能参数为弹性模量7×1010Pa，密度2 700 kg/m3，泊松比0.3；弹簧的弹性系数为140 N/m。采用ANSYS有限元仿真软件针对框架结构进行分析，其结构选用一个高阶3维10节点固体结构单元，其中弹簧采用具有轴向或扭转性能的COMBIN14单元。当只有弹簧约束的情况下，对模拟飞行器框架进行模态分析，得到前10阶模态频率和振型，其中前6阶模态振型为刚体位移，第7阶开始为振动模态，其中第7阶、第8阶、第9阶、第10阶模态分别如图4、图5、图6、图7所示，它们对应的频率分别为19.75 Hz, 34.35 Hz, 49.70 Hz, 62.50 Hz。

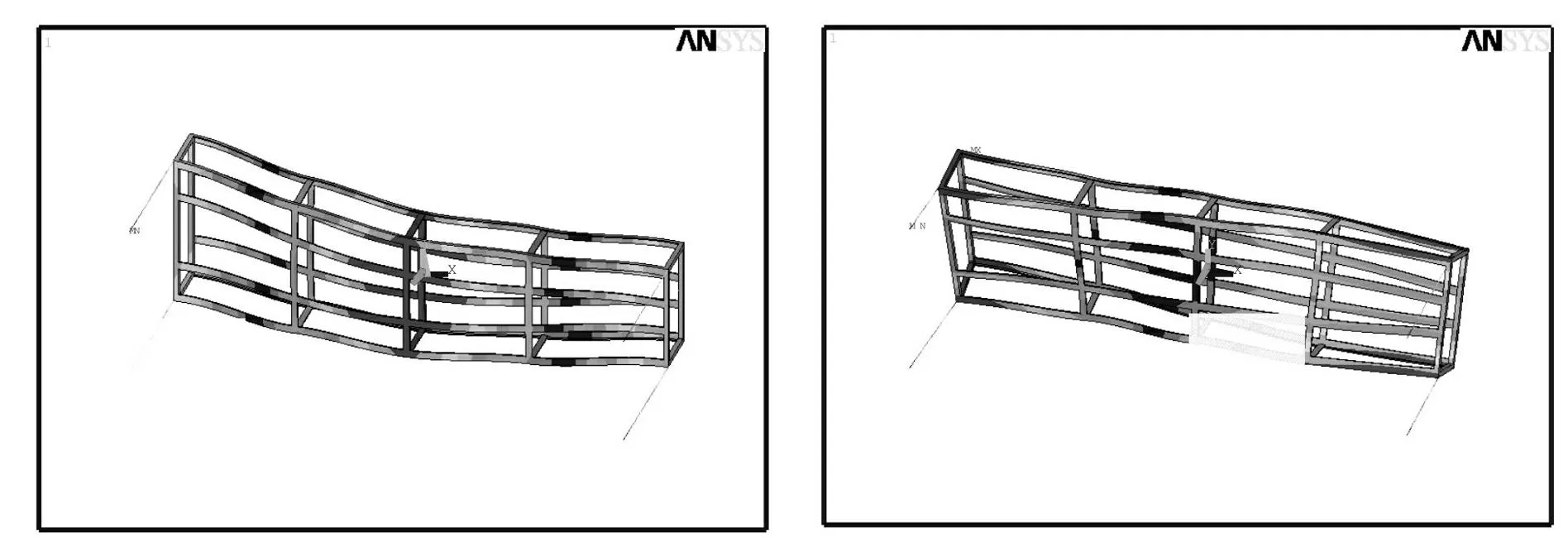
图4 第7阶模态变形图Fig.47-thordermodalstrainplot图5 第8阶模态变形图Fig.58-thordermodalstrainplot

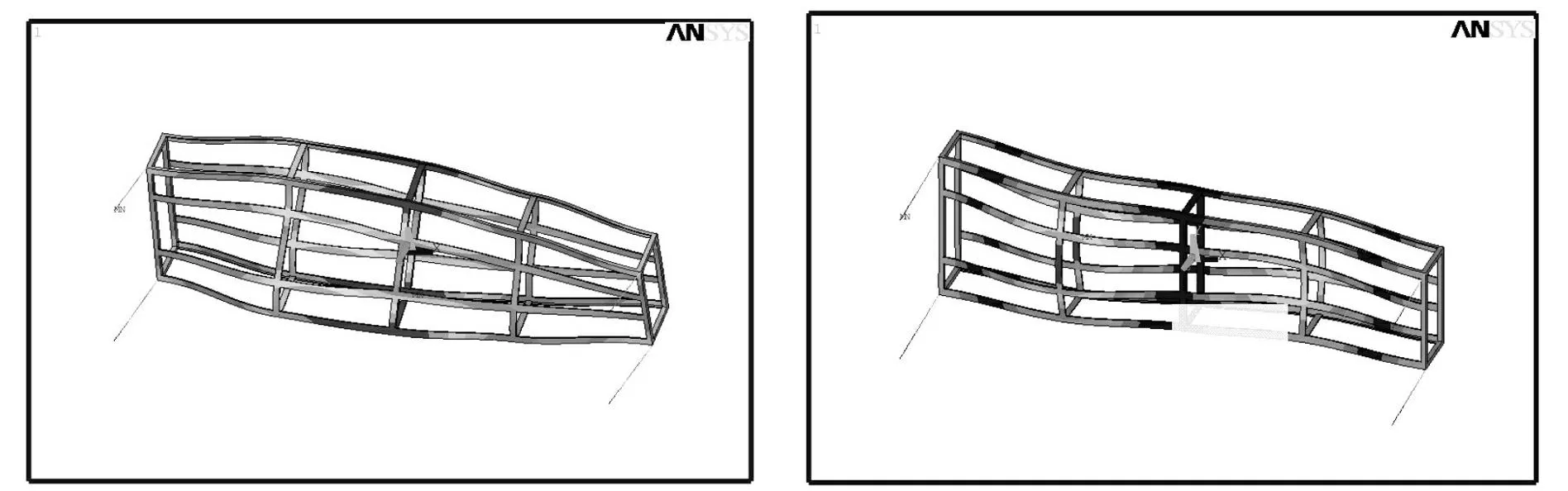
图6 第9阶模态变形图Fig.69-thordermodalstrainplot图7 第10阶模态变形图Fig.710-thordermodalstrainplot

3.2压电传感器和驱动器的优化布置

采用压电陶瓷元件作为传感器和驱动器分布式植入框架模型结构表面，同时在框架结构后端增加两个尾翅，构成模拟飞行器框架结构的压电机敏模型结构，其压电陶瓷元件的主要参数[12]为：密度7 500 kg/m3，泊松比0.32，弹性系数矩阵[D]，压电系数矩阵[e]，介电常数矩阵为对角阵[ζ]。

利用有限元软件ANSYS的参数化设计语言(APDL)，采用SOLID5单元方式建立压电片模型，同时针对压电机敏框架结构进行振动控制仿真实验，具体实验过程如下：首先对机敏框架模型结构中心施加正弦力以激励出弯曲模态振型，在压电片不施加控制时，获取压电片电压作为控制参考依据。此时该电压是变形引起的，理论上只需要施加一个相反的电压即可抵消此变形，考虑到压电片的变形很小，导致控制力较小，因此应将压电片贴在应变较大的地方。

在不断增加压电片的基础上，经过多次对比试验，发现选取应变最大位置附近的点比选取其他点的效果更好。读取n1(-0.376，0.216，0.08)和n2(-0.383，0.216，0.8)两点的Z向位移，相减后乘以放大系数10e10，施加电压到外侧的2对压电片上，对内侧的2对压电片施加相反的电压，时间步长DT=T/8=0.003 71 s，T为第7阶固有周期。循环计算10个周期(大约0.296 8 s)，压电机敏结构逐渐得到了有效的振动控制，其控制效果见图8，在施加控制了5个周期(约0.15 s)的时候，框架模型结构振动幅度明显减小，约为自由振动时最大振幅的1/3。

图8　压电机敏框架结构控制效果图Fig.8 Control performance of thepiezoelectric smart framework

由上述分析可知，结构振动应力大的点比较适合布置传感器，驱动器应该布置在传感器的附近；同时依据各阶振动模态的应力变化，综合考虑在相关位置进行压电传感器/驱动器的配位布置，具体配位布置见图9。图9中布置在骨架上的驱动器每一纵排为一个驱动通道，尾部机翼上的驱动器每一横排为一个通道，传感器各自为各自的通道，一共构成10×10的多通道控制模型，而在实际的实验中，由于外接设备的通道数的限制，一般采用8×8多通道进行控制，根据实际情况舍弃其中2个通道。

图9　压电传感器/驱动器布置图Fig.9 Configuration of PZT sensors and actuators

3.3实验平台构建

实验平台主要由固定支撑铝合金外框架、模拟飞行器框架结构的压电机敏模型结构、信号发生器、功率放大器、电荷放大器、低通滤波器、高速数据AD采集卡与DA输出卡、高性能计算机、示波器以及相关测控单元等组成(见图10)。

图10　实验平台示意图Fig.10 Schematic diagram of the experiment platform

使用橡皮绳将压电机敏框架模型结构吊装在铝合金外框架上，使用可调节夹持装置将激振器固定于铝合金外框架上；任意函数信号发生器(型号：33220A)输出激励信号经过功率放大器(型号: Model 7602)作用到激振器，通过激振器对模拟飞行器结构施加的激励力使之产生相应的振动响应；粘贴的多路压电传感器检测到结构振动信号，经过电荷放大器(型号：YE5852A)的调理，输出到以PCI接口连接到计算机的高速AD采集卡(型号：PCI-1712)，而后依据所开发的软件平台并依照相应的控制策略运算产生期望的多路控制信号，通过DA输出卡(型号：PCI-1721)输出，并经压电功率放大器放大，输出到各组压电作动器，从而对实验模型结构产生控制作用力，实现对其结构振动响应的实时抵消，以达到主动消除或降低模型结构振动响应的目的，计算机程序同时完成对振动数据的处理、分析、存储和显示功能。其实际实验平台(见图11)。

图11　实验平台整体实物图Fig.11 Photo of the experiment platform

4实验分析与验证

4.1FULMS与改进型FULMS算法仿真

针对多通道自适应滤波前馈FULMS控制算法进行了仿真试验，参考信号直接取自于激励源信号(即假定的外扰信号)，并针对实验模型结构通过离线自适应建模方法，获得实测多路控制通道模型辨识向量作为仿真的受控通道模型参数；在其它参数一致的情况下，采用本文所提的改进型控制算法与常规的FULMS控制算法进行对比仿真实验，其仿真对比结果如图12～图15所示。其中，图13和图15中的曲线为滤波器权系数的权值调整过程，从上至下的每条曲线分别表示为W1、W2、W3、…、Wn的变化情况，其中n为滤波器阶数；从图中可以看出，改进算法比常规的FULMS算法收敛速度较慢，但控制效果良好，通过牺牲收敛速度来换取算法的实用性，还是值得的。

图12　常规FULMS的控制效果Fig.12 Control performance of classic FULMS

图13 常规FULMS控制器权系数收敛曲线Fig.13WeightconvergencecurveofclassicFULMScontroller图14 改进型FULMS的控制效果Fig.14ControlperformanceofimprovedFULMS图15 改进型FULMS控制器权系数收敛曲线Fig.15Weightconvergencecurveofimprovedcontroller

4.2改进型FULMS控制算法实验

当压电机敏框架模型结构被激振器持续激励，并处于100 Hz频率以下激振范围内，采用上述改进型FULMS振动控制算法，进行8输入8输出的多通道自适应滤波振动主动控制实验；在8路通道中，第7路和第8路分别为实验模型的左右两个尾翼，其它6路为实验模型的框架结构；在实验过程中，针对第7阶至第10阶弯曲模态进行了实际的控制实验。在实验过程中，当施加控制后，逐渐地抑制了结构的某阶模态响应时，将激振频率突然改变又激起新的某阶模态，则控制算法在重新调整权值后仍可迅速抑制新的结构响应，从而表明这一控制方法不但具有很高的控制修正速率，而且具有较强的适应外界变化的能力。

针对压电机敏框架模型结构的振动主动控制实验过程大致为如下几个步骤：

(1)利用信号发生器输出7～10阶模态频率其中的一个频率的正弦激励信号，驱动激振器对其实验模型结构产生持续振动。

(2)基于所开发的测控程序，首先对控制通道模型辨识的参数进行设置，然后对其进行辨识，直至辨识完成。

(3)然后设置进行控制参数设置，如采样频率、滤波器阶数、步长因子等。

(4)点击控制按钮，对实验模型结构施加振动主动控制算法，控制效果将逐渐获得体现。

(5)控制过程中，实时保存相关数据，为实验分析做准备。

从连续四阶模态频率中任选一个频率作为激振频率，此次实验激振频率为20.65 Hz，控制通道模型选用离线辨识结果，前馈滤波器长度为12，反馈滤波器长度也为12，前馈收敛步长为μ=0.000 2，反馈前馈收敛步长为a=0.000 1，依据控制算法，进行8输入8输出的多通道自适应滤波振动主动控制试验，由于篇幅有限，在8个通道中只取4个通道的控制效果作为代表，其中4个通道分别为第1通道、左右尾翼的两个通道(即第7、第8通道)、第5通道；其控制效果见图16～图20。

图16、图17、图18、图19分别为左右尾翼、通道1和通道6的振动响应时间历程，大约在8s左右的时候，就可有效抑制模型结构振动响应；图20为实验模型结构振动响应总体抑制效果图(即每个传感信号的最小均方误差(MSE)相加之和)，由图20可知，施加控制后模型结构总体响应明显下降，表明结构总体振动获得有效抑制；图21为控制过程中参考信号时间历程，从图21可知，经过控制算法合成的参考信号与激振信号有很强的相关性。

图16 左翼形结构振动响应时间历程Fig.16Responsetimehistoryoftheleftwing图17 右翼形结构振动响应时间历程Fig.17Responsetimehistoryoftherightwing图18 通道1的振动响应时间历程Fig.18Responsetimehistoryofchannel1

图19 通道5的振动响应时间历程Fig.19Responsetimehistoryofchannel5图20 结构振动响应总体抑制效果图Fig.20Overallvibrationcontrolperformance图21 控制过程中参考信号时间历程Fig.21Referencesignaltimehistory

5结论

本文给出了一种直接从振动结构响应中提取参考信号的改进型FULMS控制算法，构建了模拟飞行器框架结构的压电机敏实验模型进行方法验证；经过仿真和实验分析，与常规FULMS算法相比，改进型FULMS控制算法虽然收敛速度较慢，但控制效果良好，尤其是针对线性控制系统有效解决了参考信号实际获取问题，从而提高了FULMS结构振动控制算法的实用性；同时相关技术方法的探索和验证，为进一步深入研究奠定了基础。

参考文献

[1]王艳奎.临近空间飞行器应用前景及发展概况分析[J]. 中国航天, 2009, 10: 39-44.

WANG Yan-kui. Analysis of development status for Near space vehicles [J]. Aerospace China, 2009, 10: 39-44.

[2]陈勇,熊克,王鑫伟,等.飞行器智能结构系统研究进展与关键问题[J]. 航空学报, 2004, 25(1): 21-25.

CHEN Yong, XIONG Ke, WANG Xin-wei, et al. Progress and challenges in aeronautical smart structure systems[J]. Acta Aeronautica Et Astronautica Sinica, 2004, 25(1): 21-25.

[3]袁宏杰,唐环,姜同敏. 飞行器助推段振动环境分析[J]. 北京航空航天大学学报, 2006, 32(7): 760-763.

YUAN Hong-jie, TANG Huan, JIANG Tong-min. Analysis of nonstationary random vibration data during lift-off[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(7):760-763.

[4]Hildebrand R, Keskinen E, Navarrete J A R. Vehicle vibrating on a soft compacting soil half-space: Ground vibrations, terrain damage, and vehicle vibrations[J].Journal of Terramechanics,2008, 45(4): 121-136.

[5]Engel D, Meywerk M. Self-exited drive train vibrations in full-vehicle design space analysis [C]. 14th International Conference and Trade Exhibition on Numerical Analysis and Simulation in Vehicle Engineering, Germany, 2008, 2031: 465-484.

[6]Huang Yon-gan, Deng Zi-chen. Decentralized sliding mode control for a spacecraft flexible appendage based on finite element method[J]. Chinese Journal of Aeronautics, 2005, 18(3): 230-236.

[7]段丽玮,汤忠梁,吴志华.飞行器垂直尾翼H∞鲁棒振动主动控制[J]. 振动、测试与诊断, 2011, 31(1): 119-123.

DUAN Li-wei, TANG Zhong-liang, WU Zhi-hua. Active vibration suppression of vertical tail using H∞robust control theory[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(1): 119-123.

[8]Ozcelik I, Kale I, Baykal B. Recursive lease squares implementation of the quadratically constrained IIR filter[J]. IEEE Signal Processing Letters, 2004, 11(2): 144-147.

[9]Kim H W. Park H S, Lee S K, et al. Modified-filtered-u LMS algorithm for active noise control and its application to a short acoustic duct[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 475-484.

[10]Cheng Yuan-chang, Neural filtered-U algorithm for the application of active noise control system with correction terms momentum[J]. Digital Signal Processing, 2010, 20(4): 1019-1026.

[11]朱晓锦, 黄全振, 高志远,等.多通道FULMS自适应前馈振动控制算法分析与验证[J].振动与冲击, 2011, 30(4):198-204.

ZHU Xiao-jin, HUANG Quan-zhen, GAO Zhi-yuan,et al.Analysis and verification of multi-channel FULMS algorithm for adaptive feedforward active vibration control[J].Journal of Vibration and Shock, 2011, 30(4):198-204.

[12]黄全振. 压电智能结构自适应滤波振动主动控制研究[D]. 上海:上海大学, 2012.