钢管约束混凝土抗侵彻机理的数值模拟

蒋志刚，甄　明,2，刘　飞，谭清华，宋殿义

(1.国防科学技术大学指挥军官基础教育学院交通工程运输系,长沙　410072;2.航天科学与工程学院,长沙　410072)

第一作者蒋志刚男，博士，教授，1961年生

钢管约束混凝土抗侵彻机理的数值模拟

蒋志刚1，甄明1,2，刘飞1，谭清华1，宋殿义1

(1.国防科学技术大学指挥军官基础教育学院交通工程运输系,长沙410072;2.航天科学与工程学院,长沙410072)

摘要：基于侵彻试验，运用LY-DYNA软件，有限元法和光滑粒子法相结合，采用混凝土连续帽盖模型，对12.7 mm穿甲弹侵彻小直径钢管约束混凝土厚靶机理进行了数值模拟研究。研究表明：数值模拟结果与侵彻试验吻合较好，可较好地反映钢管约束混凝土靶核心混凝土侧面环向裂纹；钢管对核心混凝土的约束作用主要发生在弹丸扩孔过程；核心混凝土侧面环向裂纹的形成是入射压缩波与靶体背面反射拉伸波及钢管约束效应共同作用的结果；钢管约束混凝土靶的抗侵彻能力优于无钢管约束混凝土靶。

关键词：防护工程;约束混凝土;侵彻机理;数值模拟

基金项目：国家自然科学基金(51308539);国防科学技术大学创新资助(S130901)

收稿日期：2014-01-27修改稿收到日期：2014-06-24

通信作者甄明男，博士生，1989年生

中图分类号:O383；TB33

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.11.001

Abstract:Based on penetration tests, the penetration mechanism of steel tube confined concrete targets against 12.7 mm armor piercing projectile(APP) was simulated with LY-DYNA software, the finite element-smooth particle hydrodynamics method and the CSCMCONCRETE model. The results showed that the simulation results agree well with the test data, they can better reflect the hoop cracks on side faces of the steel tube confined concrete; the confinement effect of steel tube on the confined concrete inures during the projectile expanding; the formation of the hoop cracks on side faces of the confined concrete is the inter-action results of the incident compression wave, reflected stretching wave from target back face and the confinement of the steel tube; the anti-penetration ability of the steel tube confined concrete target is higher than that of the normal concrete target without steel tube confining.

Simulation of anti-penetration mechanism of steel tube confined concrete

JIANGZhi-gang1,ZHENMing1,2,LIUFei1,TANQing-hua1,SONGDian-yi1(1. College of Basic Education, National Univ. Of Defense Technology, Changsha 410072, China;2. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410072, China)

Key words:protective engineering; confined concrete; penetration mechanism; simulation

钢管混凝土已广泛应用于受压为主的柱、拱等构件[1]。许多学者对钢管混凝土的静力性能[2]、抗冲击性能[3]和抗爆性能[4]进行了研究，但对其抗侵彻性能和机理研究很少。本文进行了12.7 mm穿甲弹侵彻小直径钢管约束混凝土厚靶试验，表明钢管约束混凝土靶的抗侵彻性能优于无钢管约束混凝土靶，且发现在弹丸高速冲击下，钢管约束混凝土靶的核心混凝土侧面形成了现有混凝土靶侵彻试验中没有见到过的环向裂纹区；基于侵彻试验，运用LY-DYNA软件，采用有限元-光滑粒子法[5]和混凝土连续帽盖模型[6-7]，分析了弹丸侵彻钢管约束混凝土的过程和钢管的约束作用，揭示了钢管约束混凝土的抗侵彻机理。

1侵彻试验简介

为了探索约束混凝土的抗侵机理，并为数值模拟提供依据，进行了Q235钢管约束混凝土和PVC管混凝土厚靶侵彻试验，详细情况见文献[8]。试验弹丸为12.7 mm穿甲弹，质量48 g，结构组成见图1[9]，其中卵形头钢芯，直径10.1 mm，长53 mm，质量30 g。钢芯试验后未发生变形，可视为刚体。钢管外径140 mm，壁厚3.5 mm；PVC管外径315 mm，壁厚2 mm；所有靶厚为300 mm。PVC管的强度和变形能力均很低，对混凝土的约束作用很小，因此PVC管混凝土相当于无约束混凝土。混凝土(无粗骨料)密度ρ=2 200 kg/m3，标准立方体的抗压强度和劈裂抗拉强度分别为62.3 MPa和4.52 MPa。

图1　12.7 mm穿甲弹弹丸组成Fig.1 Composition of 12.7mm APP

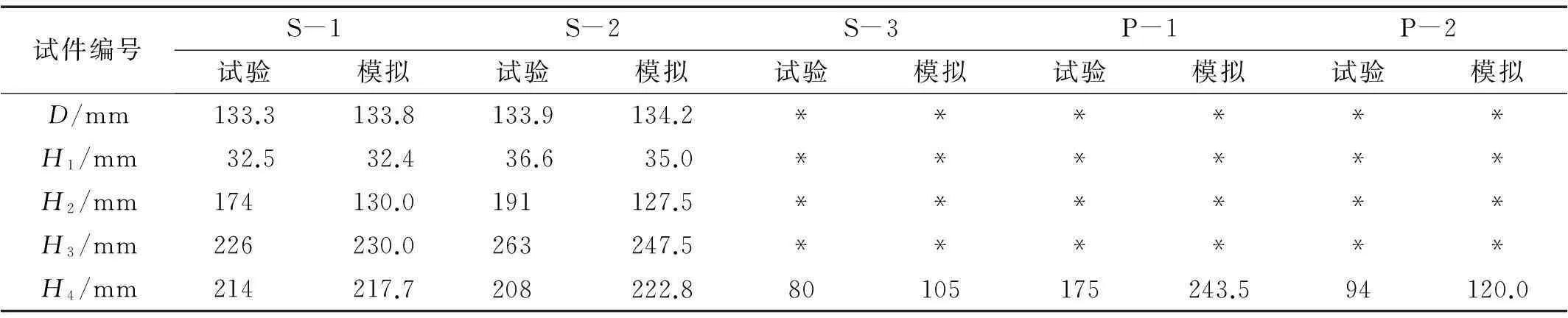
典型试验结果见表1和图2。其中：Δd为弹丸着靶偏心距，v0为着靶速度，D为漏斗坑直径，H1为漏斗坑深度，H2和H3为主裂纹位置到迎弹面的距离，H4为侵彻深度；钢管约束混凝土试件S-1、S-2和S-3分别对应于文献[8]试件4#、1#和18#第一发，PVC管混凝土试件P-1和P-2分别对应于文献[8]试件10#和12#。在PVC管混凝土靶试验中，弹丸未能嵌于混凝土中，而是带着剩余动能飞离了混凝土靶，侵彻深度根据试验后混凝土上的弹痕测得，因此试件P-1和P-2的H4数据可能小于半无限混凝土靶的侵彻深度，且着靶速度越高，差别将越大。从表1和图2可知：v0≈540 m/s时，钢管约束混凝土靶(S-3)的侵彻深度比PVC管混凝土靶(P-2)约小15%；钢管约束混凝土靶侵彻后保持完整，具有抗多发打击能力；钢管约束混凝土靶的破坏模式与半无限混凝土靶的最大差别是：由于钢管的约束作用，核心混凝土侧面出现了环向裂纹。

表1　钢管混凝土靶典型试验结果

注：表中*表示未测量或无需测量的数据。

图2　靶的典型破坏情况Fig.2 Typical failure modes of targets

2侵彻试验的数值模拟

2.1计算模型

通过对表1侵彻试验进行数值模拟，确定计算模型及参数。数值模拟中，假设钢管约束混凝土靶正面(迎弹面)、背面和钢管侧面均为自由边界，并忽略重力的影响；忽略PVC管的作用，假设PVC管混凝土靶外边界为自由边界。为了体现混凝土飞溅现象和避免有限元网格畸变，并考虑计算效率，弹孔附近圆柱形区域内采用光滑粒子模型，其余采用有限元模型。鉴于问题的对称性，建立1/2结构有限元-光滑粒子模型(FEM-SPH)(见图3)。弹丸和钢管均采用SOLID164八节点实体单元，弹丸单元特征尺度小于1 mm，共划分4 658个单元；钢管单元尺寸为5.5 mm×1.75 mm×2.5 mm，共划分7 200个单元。经试算，取光滑粒子区域半径为25 mm(约为弹丸半径的4倍)较为合适，该区域先通过有限元软件形成网格，再由网格形成光滑粒子，粒子间距1.5 mm，共划分36 000个粒子单元；外围混凝土采用SOLID164八节点实体单元，径向渐变网格划分，内侧网格较密(最小单元尺寸2.5 mm×2 mm×2.5 mm)，其他区域网格稀疏(最大单元尺寸7 mm×4 mm×2.5 mm)，共划分54 000个单元。弹丸铅套、铜皮和钢芯的接触面均采用面-面侵蚀接触(CONTACT_ ERODING_ SURFACE_TO_SURFACE)；混凝土光滑粒子区域与弹丸铅套、铜皮和钢芯之间采用点-面侵蚀接触(CONTACT_ERODING_ NODES_TO_ SURFACE)；混凝土光滑粒子区域和有限元网格区域界面采用点-面连接接触(CONTACT_ TIED_ NODES_TO_SURFACE)。混凝土与钢管内壁接触面按固结处理，不考虑滑移。在对称面上定义对称边界条件，对网格节点的自由度进行约束，同时对处于对称边界的光滑粒子使用“虚粒子”，以保证对称边界处粒子不会穿越对称面。

弹丸钢芯采用刚体材料模型(RIGID)，弹丸铅套和钢管采用弹塑性随动硬化材料模型(PLASTIC_KINEMATIC)，铜皮采用JOHNSON_COOK(J-C)模型和GRUNEISEN状态方程。材料模型参数按文献[9-10]确定，见表2和表3。

混凝土采用连续帽盖模型(MAT_CSCM_CONCRETE)[6-7]，该模型简单实用，能较好地体现钢管约束混凝土侵彻试验中发生环向裂纹的新现象。CSCM模型采用损伤变量d体现混凝土材料的破坏，并通过损伤变量d对应力、弹性模量等进行折减，即：

(1)

图3　靶体和弹体计算模型Fig.3 Finite element models of target and projectile

材料密度/(kg·m-3)弹性模量/GPa泊松比屈服强度/MPa切线模量/GPa硬化参数铅套1134018.40.3752001.0钢管78501980.32351.01.0

表3　铜皮J-C模型及GRUNEISEN状态方程主要参数

2.2模拟结果

对表1中侵彻试验进行数值模拟，得到的靶体破坏现象见图4，图4中，右侧为材料损伤标尺，数字越大表示材料损伤越严重。破坏参数模拟结果与试验结果的比较见表4。

比较图2和图4可知，数值模拟破坏现象与试验吻合较好。图4(a)中，S-1正面混凝土漏斗坑和飞溅现象明显，纵剖面弹孔周围混凝土都出现了稀疏的损伤带，夹弹处出现了较密集的严重损伤带，侧面出现了严重的环向损伤带(即环向裂纹区)；图4(b)中，P-1正面径向裂纹明显。须指出，模拟中的接触算法在搜索单元时存在时间差，产生了不对称的侵彻阻力，导致垂直入射的模拟结果中弹丸出现了轻微的偏转。

由表4可得：

(1)钢管约束混凝土靶，高速打击下(S-1、S-2)漏斗坑损伤尺寸的数值模拟与试验结果吻合很好，误差小于5%；侵彻深度H4也吻合很好，最大误差为7.1%；主裂纹位置H3最大误差不超过8%。但是，H2最大误差达到50%，这是因为数值模拟中的材料是理想均匀材料，而试验中的混凝土材料不均匀，裂纹发展具有较大的随机性。低速打击下(S-3)，侵深模拟结果比试验高31.2%，其主要原因是侵彻试验通过减少弹丸装药来实现低速打击，导致弹丸在飞行过程中漂移，弹丸着靶时为斜入射(见图5)，弹丸侵彻能力降低，从而减小了侵彻深度，而数值模拟中的弹丸是垂直入射，因此低速打击下侵深的模拟结果比试验高。

图4　靶的破坏情况，数值模拟Fig.4 Typical failure modes of simulations

试件编号S-1S-2S-3P-1P-2试验模拟试验模拟试验模拟试验模拟试验模拟D/mm133.3133.8133.9134.2******H1/mm32.532.436.635.0******p/mm174130.0191127.5******h1/mm226230.0263247.5******p/mm214217.7208222.880105175243.594120.0

(2)PVC管混凝土靶侵彻深度的模拟结果比试验大很多，且着靶速度越高，差别越大。其主要原因：一是试验中弹丸未能嵌于PVC管混凝土，而是带着剩余动能飞离混凝土，导致表1的H4数据偏小；二是低速打击试验中弹丸着靶姿态为斜入射，侵彻能力降低。

(3)PVC管混凝土靶侵彻深度模拟结果与钢管约束混凝土靶相比，高速侵彻时大9.3%(P-1与S-2相比)，低速侵彻时大14.3%(P-2与S-3相比)。这与试验结果基本一致。因此，钢管约束混凝土的抗侵彻能力优于无钢管约束混凝土。

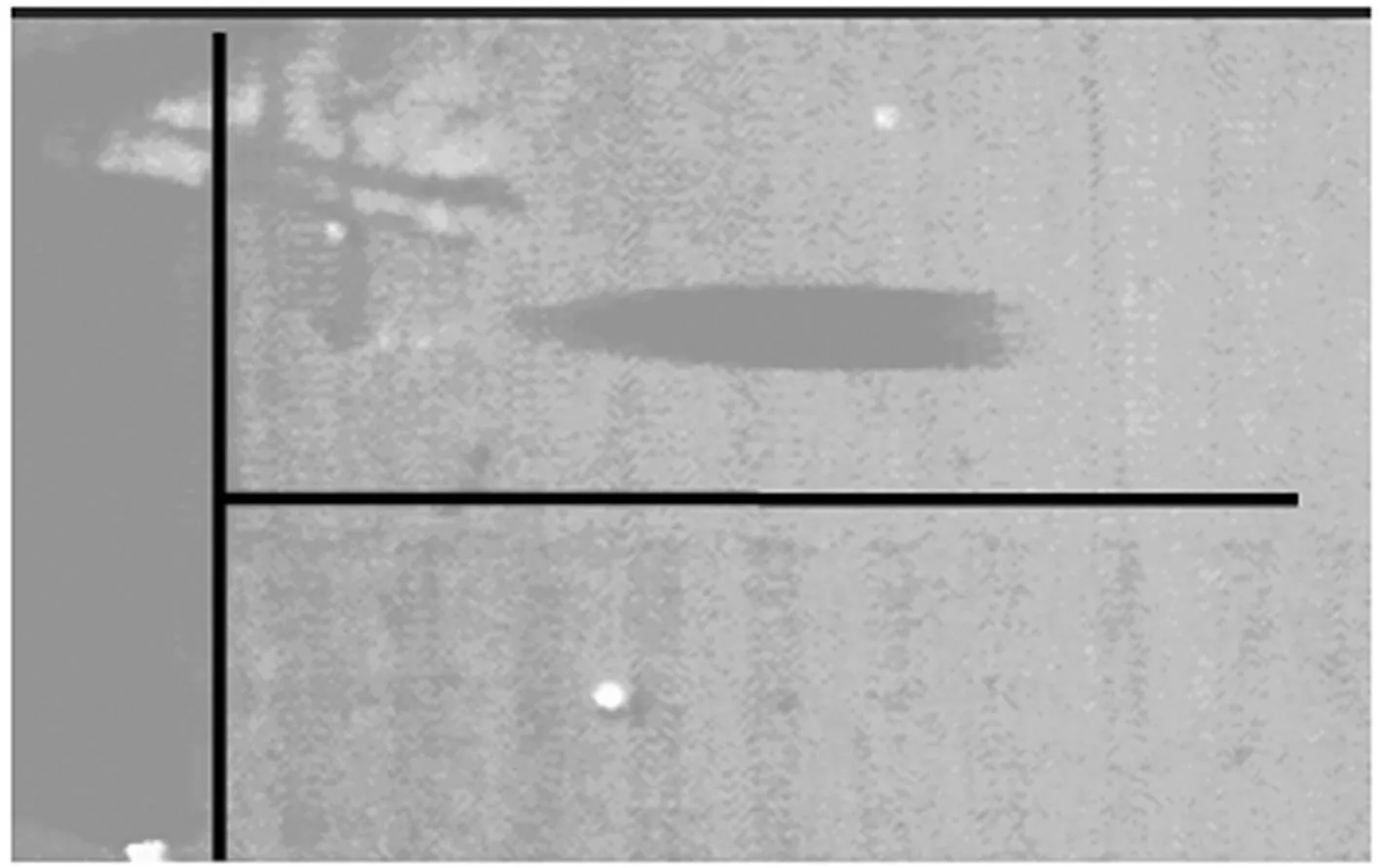
图5　弹丸着靶前姿态图(541.5 m/s，高速摄像)Fig.5 Impact situation of projectile

综上所述，钢管约束混凝土靶侵彻试验数值模拟得到的破坏形式和破坏参数等均与试验结果取得了良好的一致性，表明本文采用的算法、单元类型和材料模型与参数等合理可行。

3机理分析

3.1侵彻过程分析

以S-1(Δd=0 mm，v=833.3 m/s，垂直入射)为例，分析侵彻过程。图6至图8分别给出了钢芯的位移、速度和加速度时程曲线，图9给出了侵彻过程中典型时刻的混凝土损伤云图。图9中，左图为纵剖面，中图为侧面，右图为迎弹面。需指出，为方便建模，数值模拟建模时弹丸与靶体迎弹面留有0.8 mm间隙，此间弹丸飞行时间约1 μs，因此可近似将t=0时刻作为侵彻开始时刻。

综合图6～图9，可得核心混凝土的损伤发展过程：

(1)漏斗坑和环形裂纹形成阶段。当t≤16 μs时，钢芯尚未接触混凝土，仅弹丸头部铜皮和铅套冲击混凝土，钢芯速度基本保持不变；其后，钢芯进入减速阶段，弹丸附近混凝土出现损伤并向四周发展，逐渐形成漏斗形损伤区；当t≈138 μs时，弹尖前约27 mm处混凝土侧面出现了第一道环形损伤区。

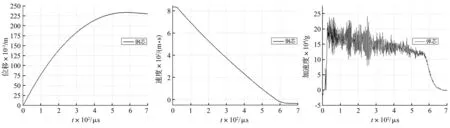
图6 钢芯位移时程曲线Fig.6Displacementtime-historycurveofsteelcore图7 钢芯速度时程曲线Fig.7Velocitytime-historycurveofsteelcore图8 钢芯加速度时程曲线(g=10m/s2)Fig.8Accelerationtime-historycurveofsteelcore

图9　侵彻过程损伤云图Fig.9 Damage of targets during penetration

(2)环形裂纹发展阶段。当t>138 μs时，随着钢芯的继续侵入，侧面第一道环形损伤区继续发展，当t≈306 μs时，弹尖前约38 mm处混凝土侧面形成了第二道环形损伤区；当t=306～566 μs时，第二道环形损伤区继续发展，t≈566 μs时，钢芯在第二道环形损伤区内停止；此后，混凝土损伤停止发展。

3.2钢管约束作用分析

为分析钢管的约束作用，取不同位置的钢管内壁单元，提取径向和环向应力时程曲线(见图10)，图10中压应力为负，拉应力为正。图10结果表明：

(1)各截面钢管内壁单元均产生了径向压力，其中B、C、D位于隧道区，其最大平均径向压力相近(在13～17 MPa之间)；A所受到的挤压作用最大，径向压力也最大(峰值达35.5 MPa)；E、F距离弹尖尚有一定距离，受到的挤压作用较小，径向压力峰值小于8 MPa。

图10　钢管内壁单元提取位置及其应力时程曲线图Fig.10 Position of steel units and stress time-history curve

(2)各点径向应力的波动规律基本一致，径向压力均存在一个上升阶段和一个稳定阶段。其中，以A点为例，当弹性压缩波到达钢管内壁时产生了径向压应力，在t≈26 μs时，出现了一个较小的压力峰值；随后，由于钢管外壁反射拉伸波的作用，产生了很小的拉应力，并在t≈30 μs时出现一个拉力峰值；此后，由于混凝土的挤压作用，径向压力迅速增大，达到峰值后趋于稳定值。

(3)在钢芯穿越某截面过程中，即在该截面附近的扩孔过程中，钢管产生了明显的径向约束作用。如B、C、D的径向压力分别从t≈30 μs、130 μs、185 μs开始迅速增大，从图6可知，此时弹尖尚未到达对应截面；当t≈110 μs、290 μs、500 μs时，B、C、D的径向压力分别达到最大，此时弹尾尚未通过对应截面。因此，钢管约束作用提高了侵彻阻力。

(4)钢管内壁单元环向均产生了拉应力，其规律与径向压力类似，在弹丸穿越某截面的过程中产生最大拉应力，弹丸完全穿过该截面后，拉应力小幅回落并趋于稳定值。

4结论

本文对12.7 mm穿甲弹侵彻钢管约束混凝土典型试验进行了数值模拟分析，结果表明：

(1)数值模拟结果与侵彻试验吻合较好，在破坏形式和破坏参数等方面均较为一致；

(2)钢管约束混凝土靶的抗侵彻性能优于无钢管约束混凝土靶；

(3)核心混凝土侧面产生环向裂纹是入射压缩波、背面反射拉伸波和钢管约束效应共同作用的结果；

(4)钢管对核心混凝土的侧向约束作用主要发生在弹丸的扩孔过程。

参考文献

[1]韩林海. 钢管混凝土结构[M]. 北京：科学出版社，2000.

[2]Sakina K, Nakahara H, Morino S, et al. Behavior of centrally loaded concrete filled steel tubes short columns[J]. Journal of Structural Engineering, 2004, 130(2):180-188.

[3]Shan J H, Chen R, Zhang W X, et al. Behavior of concrete filled tubes and confined concrete filled tubes under high speed impact[J]. Advances in Structural Engineering,2007, 10(2):209-218.

[4]Fujikura S, Bruneau M, Lopez-Garcia D. Experimental investigation of multihazard resistant bridge piers having concrete-filled steel tube under blast loading[J]. Journal of Bridge Engineering, 2008, 13(6):586-594.

[5]Meuric O F J, Sheridan J, O’Caroll C, et al. Numerical prediction of penetration into reinforced concrete using a combined grid based and meshless lagrangian approach[C]. In:10th Int. Symp. Interaction of the Effects of Munitions with Structures, San Diego, 2001.

[6]Murray Y D. Uuers manual for LS_DYNA concrete material model 159[R]. FHWA-HRT-05-062, Washington DC, 2007.

[7]Murray Y D, Abu-Odeh A, Bligh R. Evaluation of LS-DYNA concrete material model 159[R]. FHWA- HRT-05-063,Washington DC, 2007.

[8]甄明. 有限空腔膨胀理论及约束混凝土抗侵彻机理研究[D]. 长沙：国防科学技术大学，2013.

[9]侯二永. 陶瓷间隙靶抗12.7 mm穿甲燃烧弹机理及性能研究[D]. 长沙：国防科学技术大学，2008.

[10]LS-DYNA Keyword user’s manual[M]. Version 971. Livermore software Technology Corporation, 2007.

[11]沈蒲生，梁兴文. 混凝土结构设计原理[M]. 3版.北京：高等教育出版社，2007.

[12]王元丰，梁亚平. 高性能混凝土的弹性模量与泊松比[J]. 北方交通大学学报，2004，28(1)：5-7.

WANG Yuan-feng, LIANG Ya-ping.Study on modulus of elasticity and poisson ratio of high performance concrete[ J]. Journal of Northern Jiao-tong University, 2004, 28(1): 5-7.