饱和土中管桩的扭转振动特性研究

靳建明，张智卿，吴章土，李西斌

(1.浙江树人大学城建学院，杭州　310015; 2. 浙江农林大学土木工程系，杭州　311300)

第一作者靳建明男，博士，副教授，1975年生

饱和土中管桩的扭转振动特性研究

靳建明1，张智卿1，吴章土1，李西斌2

(1.浙江树人大学城建学院，杭州310015; 2. 浙江农林大学土木工程系，杭州311300)

摘要：基于Biot提出的饱和多孔介质的波动方程，研究了均质各向同性饱和土中端承管桩的扭转振动问题。首先对土层动力平衡方程进行求解并得到土体扭转振动位移形式解，然后对管桩的动力平衡方程进行求解，得到了管桩桩顶转角解析解，进一步通过数值算例分析了桩周土与桩芯土的物理力学参数对管桩桩顶复刚度和桩身转角的影响。数值分析结果表明，在动力基础设计所关注的低频段，桩周土与桩芯土的剪切模量比、壁厚以及桩的长径比对管桩的动力响应有较大的影响，而液固耦合系数的影响很小。

关键词：管桩；饱和土；桩土相互作用；扭转振动；转角

基金项目：浙江省自然科学基金资助项目(LY12D02001)；浙江省“十二五”重点学科建设项目([2012]80-291)

收稿日期：2014-03-28修改稿收到日期：2014-05-20

中图分类号:TU47

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.11.010

Abstract:Based on Biot’s dynamic wave equation for porous-saturated soil, torsional vibration of an end-supported pipe pile embedded in homogeneously isotropic saturated soil and subjected to a transient torsional loading was theoretically investigated. Firstly, the torsional vibration displacement form solution of the saturated soil was solved with the dynamic equations of soil layer. Then, by utilizing the continuity and boundary conditions of the pile-soil system and solving the dynamic equation of the pipe pile, the dynamic response of the twist angle of the pipe pile was obtained in a closed form. Finally, the influences of major soil parameters on the complex stiffness of the pile top and the twist angle of the pipe pile were analyzed. It was shown that in the low-frequency range focused by dynamic foundation design, the modulus ratio of soil around pile to inner soil, the thickness and the slenderness of pipe pile have distinct influences on the dynamic response of the pile; but the influence of the liquid-soild coupled coefficient can be neglected.

Torsional vibration of a pipe pile embedded in a porous-saturated soil

JINJian-ming1,ZHANGZhi-qing1,WUZhang-tu1,LIXi-bin2(1. Urban Planning College, Zhejiang Shuren University, Hangzhou 310015, China;2. Civil Engineering Department, Zhejiang Agriculture and Forestry University, Hangzhou 311300, China)

Key words:pipe pile; saturated soil; pile-soil interaction; torsional vibration; twist angle

桩基振动理论方面的研究开展于20世纪70年代。30年来桩基振动理论已经取得了丰硕的成果，尤其在实芯桩的振动理论方面的研究。在桩基的扭转振动理论研究方面，Novak等[1]将平面应变土模型应用于动力扭转荷载作用下埋置刚性基础振动特性的研究之中，给出了土扭转阻抗的解析表达式，并用解析的方法研究了弹性半空间以及下卧层为基岩的弹性土体中埋置刚性基础的扭转振动特性。之后，Rajapakse等[2-6]较细致地研究了扭转荷载作用下弹性介质中埋置弹性圆桩的动力响应问题。

然而以上这些理论均是研究实芯桩的振动特性问题，随着管桩生产、施工等技术的发展，管桩以其施工方便、承载力高、质量可靠、较为经济等优点在各种建筑基础中得到广泛的应用。急需对管桩的振动特性作进一步的分析研究，而现有的文献报道关于这方面的研究较少。基于“径向不变假定”，刘汉龙[7]推导得到了管桩振动响应时域解，但没有考虑物理量沿径向的变化，在理论上不够严格。基于三维波动方程，将桩周土、桩芯土和桩底土对桩的作用简化为文克尔弹簧，丁选明[8]通过理论推导求得了大直径管桩的振动响应时域解析表达式。基于平面应变假定，刘林超[9]在多孔介质理论的基础上研究饱和土中端承管桩的纵向振动问题。郑长杰[10]考虑土体材料的黏性阻尼和桩-土扭转耦合振动，建立了轴对称均匀黏弹性地基中PCC 桩扭转振动的定解问题，并运用Laplace变换的方法求得了频域解析解，但没有考虑土的多孔介质属性。因此，本文基于Biot提出的动力固结理论，研究了谐和激振荷载作用下均质各向同性饱和土中端承管桩的扭转振动特性，这不仅在理论上有较高价值，而且对工程实践也有一定指导作用。

1桩土耦合扭转振动问题的数学模型

1.1桩土系统动力平衡方程

本文研究的是均质各向同性饱和土层中，桩顶受谐和激振扭矩作用时，桩底为刚性支承条件下，管桩与饱和土层的耦合扭转振动问题。计算简图见图1，土层厚度为H，桩长为H，管桩的内外径分别为r2和r1(下文均以下标1表示桩周土的物理力学参数或反应量，以下标2表示桩芯土的物理力学参数或反应量)，桩顶作用有谐和激振扭矩T(t)=T0eiωt。为了便于推导，本文假定下列条件成立：

(1)桩周土与桩芯土均为饱和均质、各向同性线性弹性体，土层底部均为刚性支承边界；

(2)土层上表面为自由边界，无正应力、剪应力；

(3)桩土体系扭转振动时，桩周土及桩芯土均只发生切向位移，而水平径向及纵向位移可忽略；桩土体系振动为小变形谐和振动，桩与周围土体完全连续接触，即桩土接触界面两侧位移、力连续；

(4)桩为弹性、垂直、均匀截面管桩；

(5)桩周土与桩芯土对桩身单位面积的环向切应力分别为f1(z, t)和f2(z, t)。

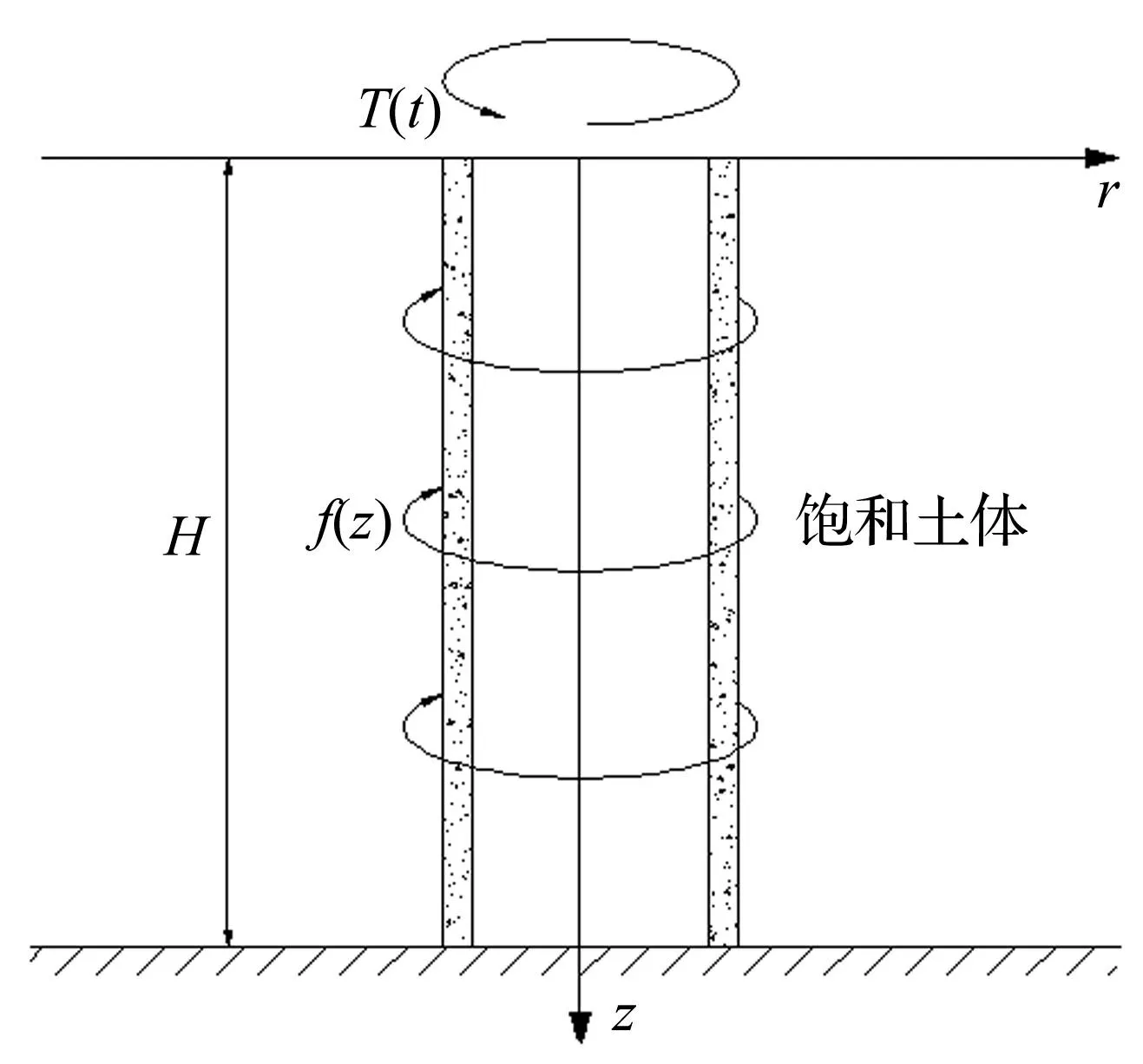
图1　桩土动力相互作用计算模型Fig.1 Computational model of pile-soil dynamic interaction

根据Biot提出的动力固结理论，忽略土颗粒的压缩性，并假设流体粘滞性包含在动力渗透系数中，令土体中任一点扭转振动的固相环向位移为uθ(r,z,t)及液相相对于固相的环向位移为wθ(r,z,t)，土体扭转振动的动力平衡方程可以表示为：

(1)

式中：ρ=(1-n)ρs+nρf为饱和土体的密度，其中ρf为流体密度，n为饱和土体的孔隙率，ρs为土颗粒密度，Gs为土的剪切模量；t为实际时间；r、z分别为径向和深度方向的空间坐标。

对于饱和土而言，流体平衡方程环向为：

(2)

式中：kd为动力渗透系数；g为重力加速度。

由于桩-土系统做发生谐和振动，所有反应量都有f(r,z,t)=f(r,z)eiωt的形式，其中f(r,z)表示振幅，ω表示圆频率。忽略eiωt项后，将式(2)代入式(1)可得：

2uθ(r,z)-

(3)

令φ(z,t)=φ(z)eiωt为桩身质点扭转振动的转角，取桩身微元体作动力平衡分析，可得桩作扭转振动基本方程如下(略去eiωt项)：

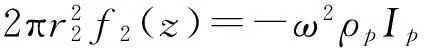
(4)

1.2定解条件

土层的边界条件为：

(5)

τθzi(r,z=0)=0，uθi(r,z=H)=0,(i=1,2)(6)

桩顶及桩底边界条件为：

(7)

桩与土接触面处的衔接条件为：

uθ1(r=r1,z)=φ(z)r1，uθ2(r=r2,z)=φ(z)r2(8)

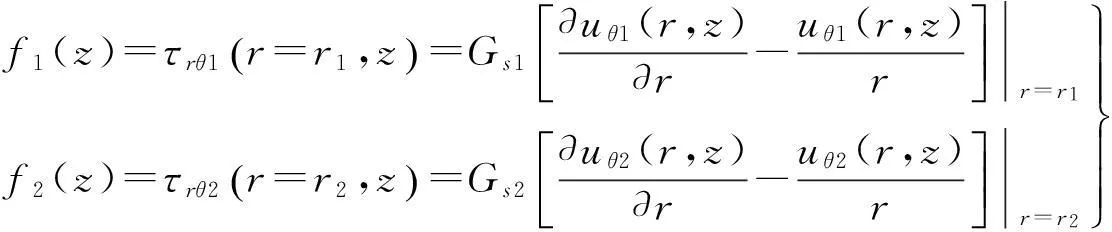
2问题求解

2.1饱和土层扭转振动问题求解

采用分离变量法，令uθ(r,z)=R(r)Z(z)并代入式(3)可得：

(10)

式(10)可以进一步分解为：

(11)

解式(11)可得：

(12)

式中：R=R(r)和Z=Z(z)为求解方程引入的单变量函数；I1(qr)、K1(qr)为一阶第一类、第二类修正的贝塞尔函数；A、B、C、D为由边界条件决定的积分常数。

由此可写出桩周土与桩芯土的位移幅值解分别为：

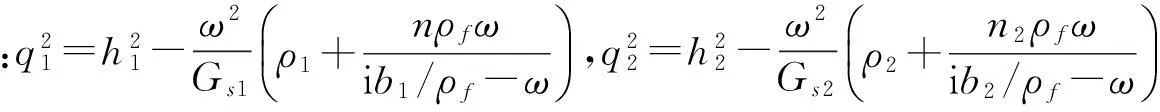
由土层边界条件式(5)可知B1=0，A2=0，由土层边界条件式(6)可得C1=C2=0以及下式：

m=1,2,3…

(14)

那么，桩周土与桩芯土扭转振动位移幅值形式解可以表示为：

(15)

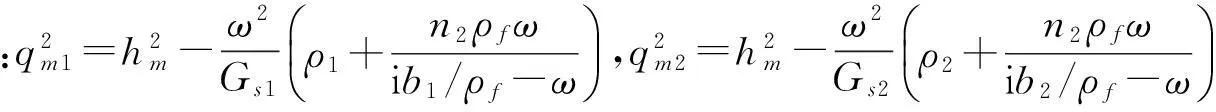
由此，结合修正贝塞尔函数的递推公式，可得桩周土与桩芯土对桩身单位面积的环向剪应力幅值τrθ分别为：

(16)

式中：I2(qm2r)、K2(qm1r)为二阶第一类、第二类修正的贝塞尔函数。

为了数值计算中参数讨论的方便，引入以下无量纲变量：

2.2桩身扭转振动问题求解

将式(9)、式(16)代入式(4)，并作无量纲化处理后，可得：

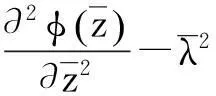
(17)

方程(17)所对应的齐次方程的通解可表示为：

(18)

方程(17)的特解形式可写为：

(19)

将式(19)代入式(17)，可以得到：

(20)

式中：

由桩土接触面的连续条件，利用固有函数cos(hmz)的正交性可得：

(21)

可以得到，管桩扭转振动时，转角响应幅值可以表示为：

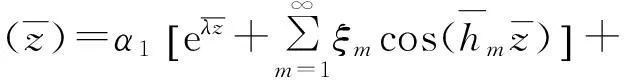
(22)

式中：

式(22)中的待定系数α1、α2可由边界条件式(7)求得：

将待定系数α1、α2代入式(22)，根据复刚度定义，可得桩顶扭转复刚度为：

(23)

3参数分析

3.1桩顶复刚度分析

以桩顶复刚度和桩顶导纳来反映管桩的振动特性。桩顶复刚度的实部代表桩的动刚度(下文用kT1表示)，虚部代表动阻尼(下文用kT2表示)。本文将主要分析桩周土和桩芯土力学行为的差异对管桩扭转振动的影响。各参量的取值为：r1=1.0 m，ρs1=2 650 kg/m3，Gs1=10 MPa，ρf=1 000 kg/m3，n1=0.5，kd1=0.001，g=10 m/s2，Gp=10 GPa。图2～图5为桩芯土与桩周土剪切模量比、液固耦合系数比、管桩内外半径比和桩长径比对桩顶复刚度的影响曲线。

图2　桩芯土与桩周土剪切模量比对桩顶复刚度的影响Fig.2 Influence of modulus ratio of soil around pile and inner soil on the complex stiffness at pile top

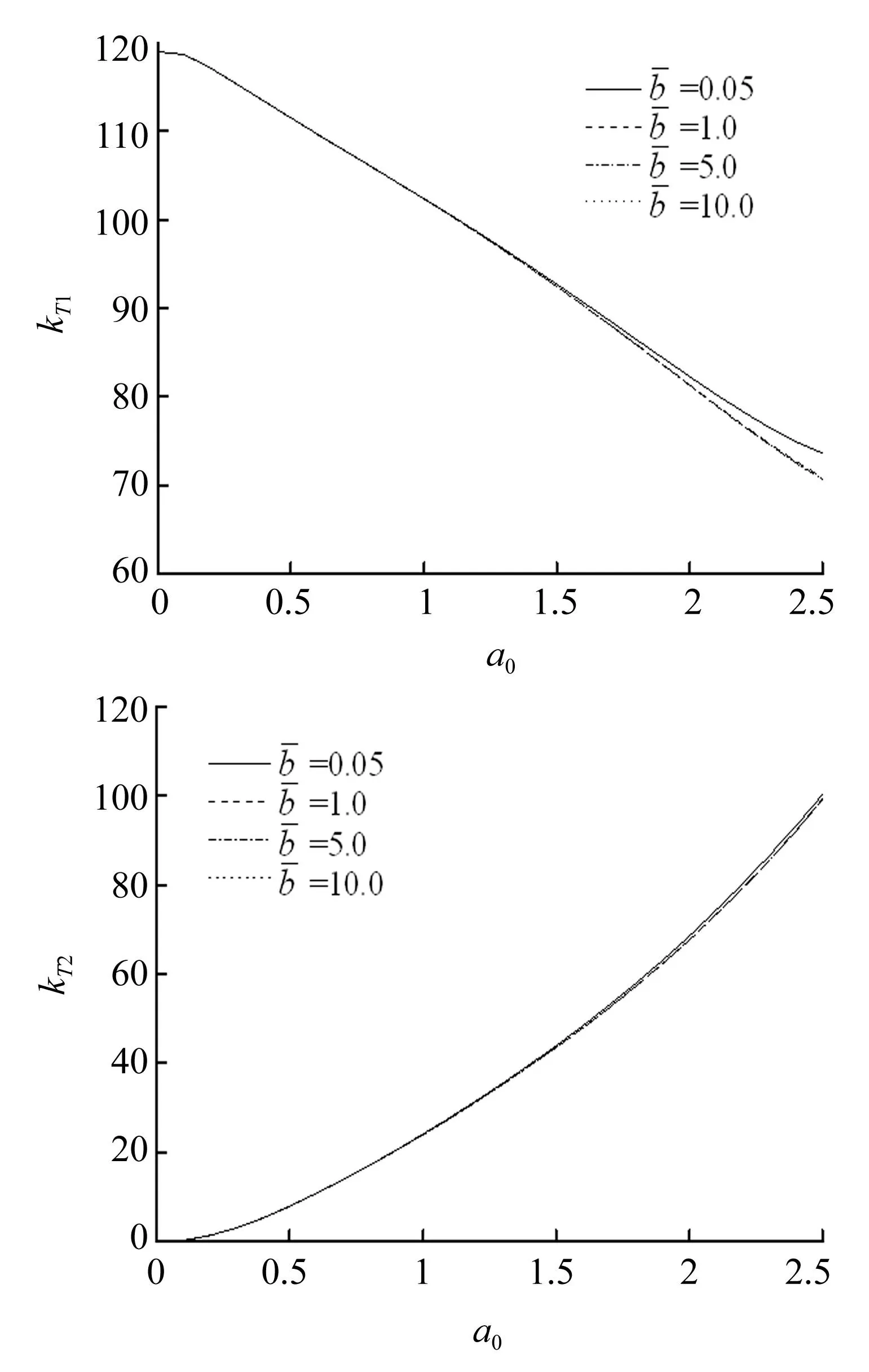
图3　液固耦合系数比对桩顶复刚度的影响Fig.3 Influence of ratio of coupled coefficient of fluid and solid phase on the complex stiffness at pile top

图4反映了管桩壁厚对桩顶复刚度的影响，可以看出，管桩壁厚对桩顶复刚度有明显的影响。桩的内外半径之比越大，复刚度越大，这是由于内外半径比较大，说明内半径相对较大，桩芯土提供的摩擦力较大，而桩周土提供的摩擦力相对较小，而复刚度却越大，可见桩周土较桩芯土对桩的扭转振动影响要大(文献[9]也获得了相同的结论)。

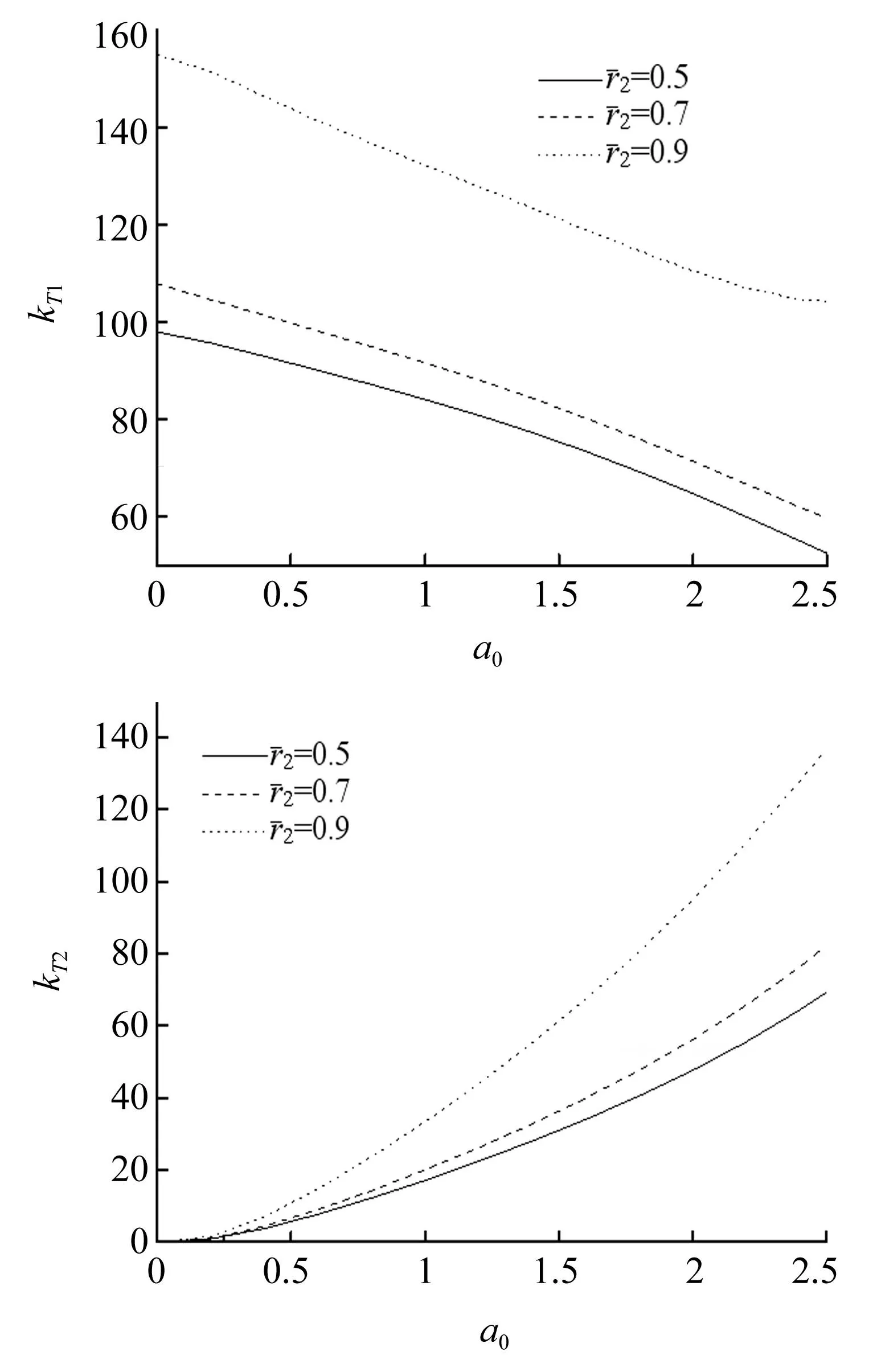
图4　管桩内外半径比对桩顶复刚度的影响Fig.4 Influence of thickness of pipe pile on the complex stiffness at pile top

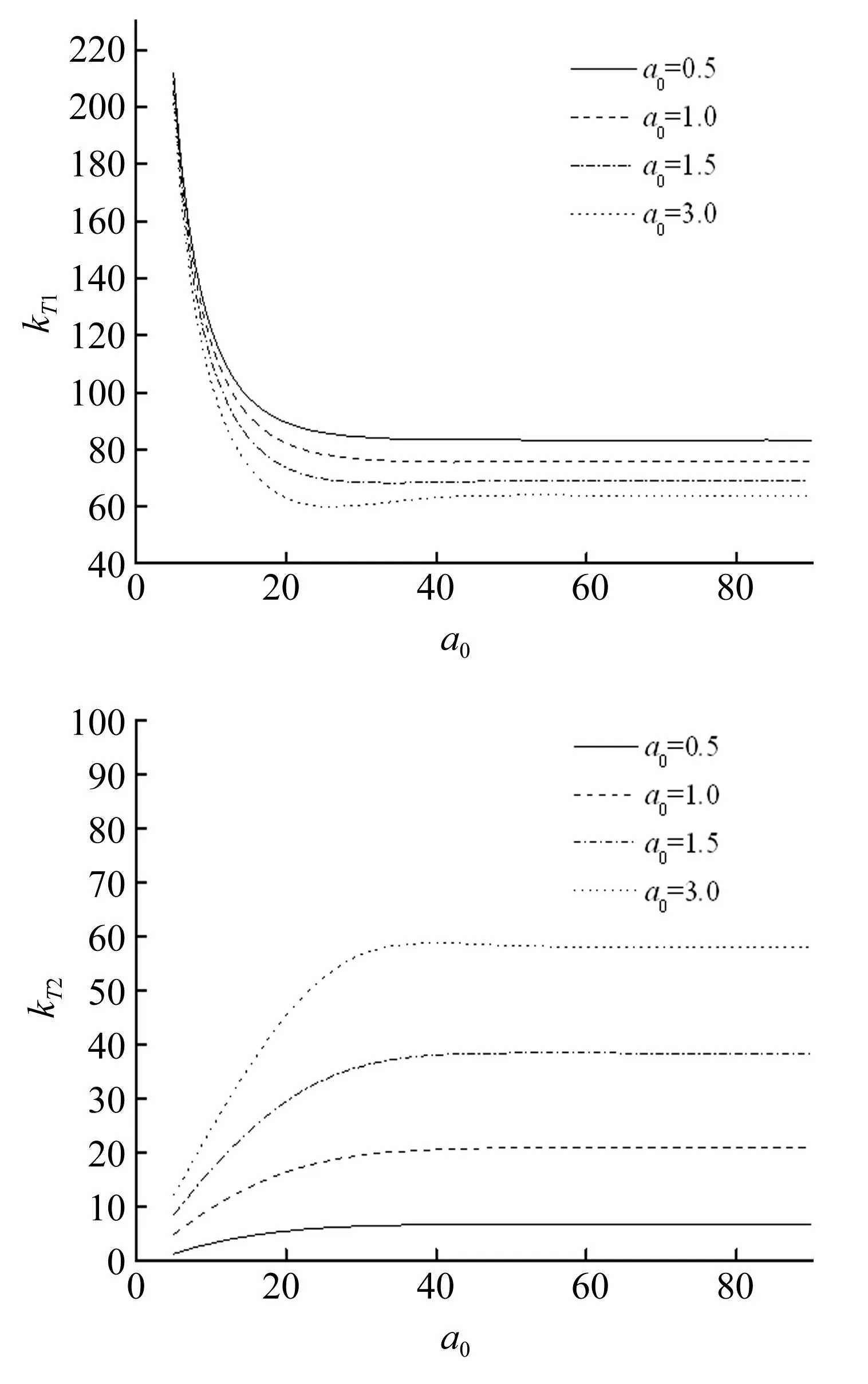
图5　管桩长径比对桩顶复刚度的影响(μ=1 000)Fig.5 Influence of slenderness of pipe pile on the complex stiffness at pile top(μ=1 000)

图5反映了桩长径比(θ)对桩顶复刚度的影响，可以发现，长径比对桩顶复刚度有显著的影响。随着桩长径比的增加，桩顶复刚度的实部和虚部均收敛为一常数。说明在一定的激振频率下，存在一个临界桩长的问题，当长径比大于此临界桩长时，桩顶复刚度就基本不再变化。

3.2桩身转角分析

频率对桩身转角有明显的影响，同时也可以发现频率对桩身转角的实部影响要小于对虚部的影响(见图6)。无量纲频率越大，桩身的位移实部越小，但虚部的绝对值增大。位移虚部沿整个桩身变化不大，而实部的变化显著，且随着激振频率的增大，其变化也越趋于平缓。

图6　不同无量纲频率荷载下桩身转角随深度变化Fig.6 Influence of non-dimensional frequency on the response of twist angle of pile

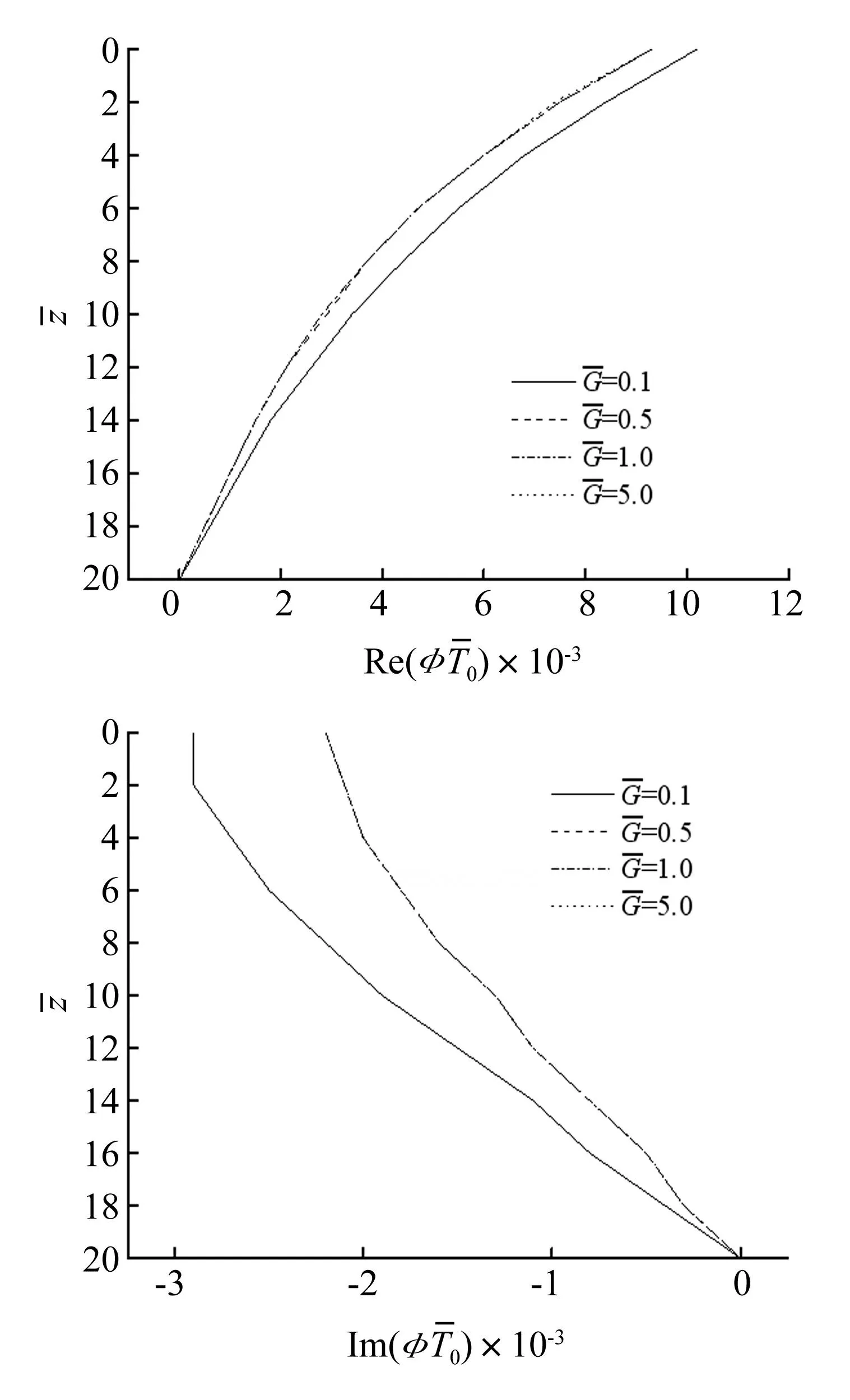
图7　桩芯土与桩周土剪切模量比对桩身转角的影响(a0=1.0)Fig.7 Influence of Gon the response of twist angle of pile (a0=1.0)

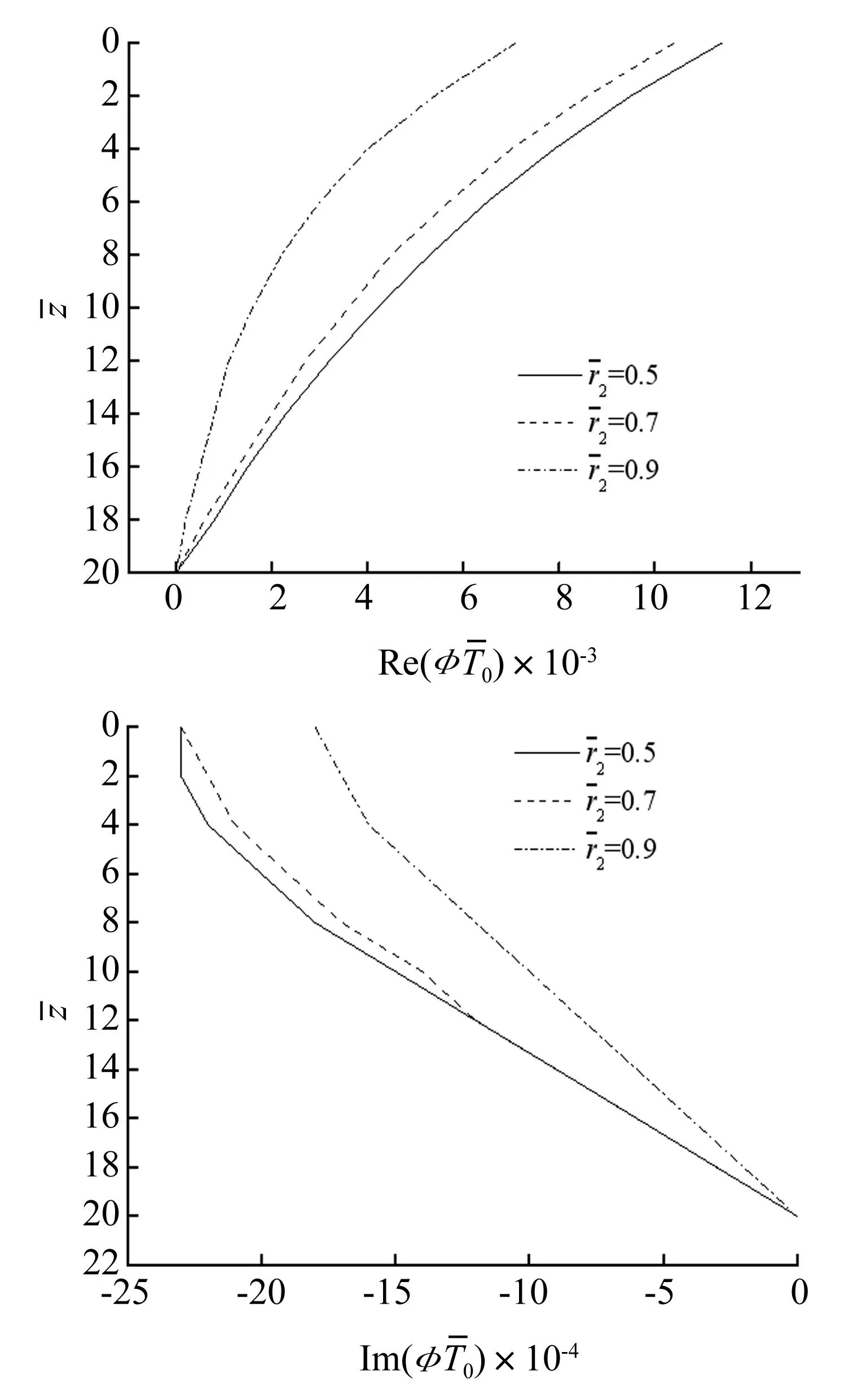
图8　管桩内外半径比对桩身转角的影响(a0=1.0)Fig.8 Influence of thickness of pipe pile on the response of twist angle of pile (a0=1.0)

4结论

基于Biot提出的动力固结理论，在三维轴对称条件下研究了谐和激振荷载作用下均质各向同性饱和土中端承桩的扭转振动特性，获得了管桩在谐和扭转激振作用下桩土耦合振动的解析解。分析了桩周土与桩芯土的物理力学参数的变化对管桩扭转振动特性影响。主要结论有：

(1)桩芯土与桩周土的液固耦合系数比的变化对管桩的扭转特性几乎没有影响。

(2)桩芯土与桩周土的剪切模量比在激振频率较低时，对管桩的振动特性影响不显著，但是随着激振频率的增大，其影响逐渐得以体现。

(3)管桩的壁厚对桩顶复刚度有明显影响，桩顶复刚度随着壁厚的减小而增大，说明了桩周土较桩芯土对桩的扭转振动影响要大。

(4)随着桩长径比的增大，桩顶复刚度逐渐趋于一恒定值，说明在一定的激振频率作用下，管桩也存在一个临界桩长。

参考文献

[1]Novak M, Howell J F. Torsional vibration of pile foundations[J]. Journal of Geotechnical Engineering Division, ASCE, 1977, 103(GT4): 271-285.

[2]Rajapakse R K N D, Shah A H, et al. Torsional vibrations of elastic foundations embedded in an elastic half-space[J]. Journal of Earthquake Engineering and Structural Dynamics, 1987,15: 279-297.

[3]Liu W M, Novak M. Dynamic response of single piles embedded in transversely isotropic layered media[J]. Earthquake Engineering and Structural Dynamics, 1994, 23: 1239-1257.

[4]Cai Y Q, Chen G, Xu C J,et al. Torsional response of pile embedded in a poroelastic medium[J]. Soil Dynamics and Earthquake Engineering, 2006, 26(12):1143-1148.

[5]Wang K H, Zhang Z Q, Leo C J, et al. Dynamic torsional response of an end bearing pile in saturated poroelastic medium[J]. Computers and Geotechnics, 2008, 35(3): 450-458.

[6]Tham L G, Cheung Y K, Lei Z X. Torsional dynamic analysis of single piles by time-domain BEM[J]. Journal of Sound and Vibration, 1994, 174(4): 505-519.

[7]刘汉龙, 丁选明. 现浇薄壁管桩低应变反射波法检测时瞬态波传播特性研究[J]. 岩土工程学报, 2008, 30(3): 414-419.

LIU Han-long, DING Xuan-ming. Propagation characteristics of transient waves in low strain integrity tests on cast-in-situ concrete thin-wall pipe piles[J]. Chinese Journal Geotechnical Engineering, 2008, 30(3): 414-419.

[8]丁选明, 刘汉龙. 大直径管桩在瞬态集中荷载作用下的振动响应时域解析解[J]. 岩土工程学报, 2013, 35(6): 1010-1017.

DING Xuan-ming, LIU Han-long. Time-domain analytical solution of the vibration response of a large-diameter pipe pile subjected to transient concentrated load[J]. Chinese Journal Geotechnical Engineering, 2013, 35(6): 1010-1017.

[9]刘林超, 闫启方. 饱和土中管桩的纵向振动特性[J]. 水利学报, 2011, 42(3): 366-372.

LIU Lin-chao，YAN Qi-fang. Vertical vibration characteristics of pipe pile in saturated soil[J]. Journal of Hydraulic Engineering, 2011, 42(3): 366-372.

[10]郑长杰, 丁选明, 刘汉龙,等. 黏弹性地基中PCC桩扭转振动响应解析方法研究[J]. 岩土力学, 2013, 34(7): 1943-1950.

ZHENG Chang-jie, DING Xuan-ming, LIU Han-long, et al. Analytic method of torsional vibration response of cast-in-place concretelarge-diameter pipe pile in viscoelastic soil[J] Rock and Soil Mechanics, 2013, 34(7): 1943-1950.