密西根大学《抽象代数》课程设置探析

李浏兰++罗李平++陈少林++刘刚

摘要：本文对密西根大学数学系《抽象代数》课程的设置进行了研究，发现其课程设置方案具有模块化、层次性和针对性等优点，为我们进行教学改革提供了参考依据。

关键词：抽象代数；课程设置；数学专业

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2015）06-0056-02

密歇根大学（University of Michigan，简称密大）是美国历史上最悠久的大学之一，在世界范围内享有极高的声誉。密歇根大学自建校以来，在各学科领域中成就卓著并拥有巨大影响，被誉为“公立常春藤”，与加州大学伯克利分校以及威斯康星大学麦迪逊分校素有“公立大学典范”之称，使得很多学生趋之若鹜。鉴于密大在美国以及在全世界教育中的地位，很多人对密大的教育进行了研究，参见[1-3]，但是鲜有人研究密大具体某门课程的设置。《抽象代数》是数学专业的必修课程，与拓扑、泛函并称为数学的新三基。因此，抽象代数是所有高校数学专业的必修课程。作者一直从事抽象代数的教学工作，深知很多学生对该门课程是望而生畏的，因此，非常关注各高校对该门课程的设置与教学情况。由于密大数学系在美国所有的大学中一直名列前茅，作者尤其关注密大数学系对该门课程的设置，总结其优点如下，对数学专业设置《抽象代数》课程提供参考依据。

一、模块化

密大数学系为本科生提供了6种可供选择的修课项目，分别是数学教学（teaching mathematics）、纯粹数学（pure mathematics）、荣誉数学（honors mathematics）、数学科学（mathematical sciences）、金融风险管理（mathematics of finance and risk management）和精算（actuarial mathematics）。作为密大数学专业的本科生，他们必须学习四年，虽然这六种修课项目有不同的要求和前提条件，但是基本的先决条件和所学的基础课程是相同的，所以学生在大一和大二期间必须先学习这些基础课程。在大二的最后阶段，学生根据各自的学习情况和兴趣爱好，通过咨询系里的导师确定修课项目，大三即按照选定的修课方案学习。精算项目旨在帮助学生通过寿险精算协会和精算师协会的考试，而风险管理项目又简称金融数学，旨在提供风险管理和金融的量化方面的教育培训。精算项目和风险管理项目所需要的金融工具主要来自于概率、统计和微分方程等领域，因此，这两个项目不要求学生学习抽象代数课程。

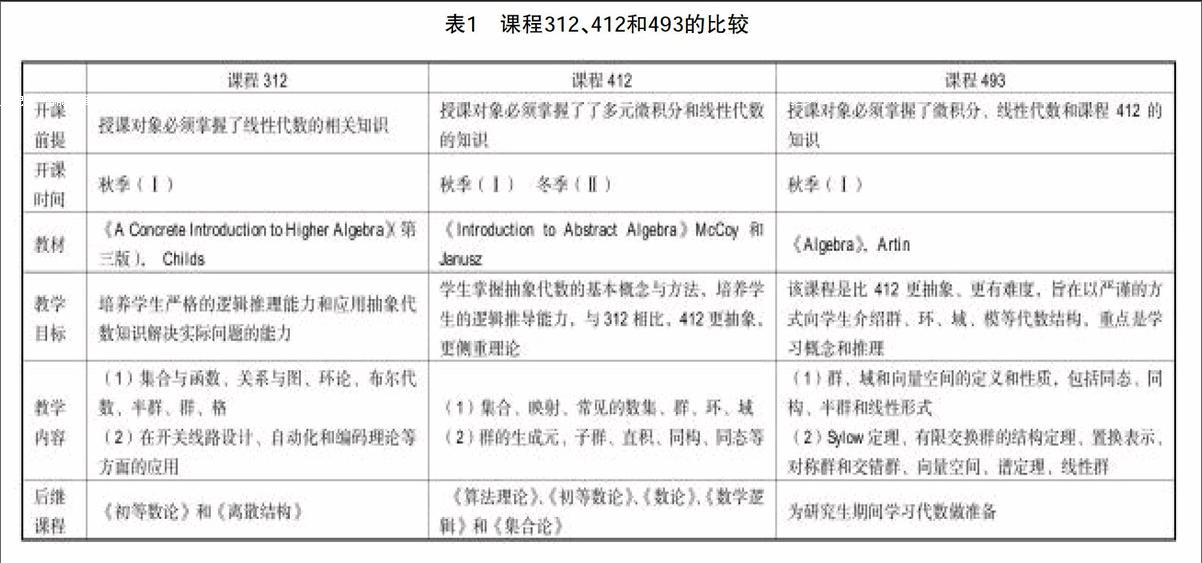
数学教学项目致力于培养中学数学教师，除了必要的高等代数知识外，还要求学生在“数论”和“抽象代数”这两门课程中任选一门作为必修课，如果学生选择学习“抽象代数”，则他们可以选择在课程312、412或493中任选一门修学（课程312、412、493见表1）。数学科学项目强调数学在其他学科中的应用，旨在培养应用数学知识解决某个领域的专业问题的能力，该项目又进一步细分成八个专业方向：控制系统、数学物理、数学生物学、数理经济学、离散和算法的方法、数值与应用分析、运筹与建模、概率方法。虽然这八个方向的具体专业要求不同，但是学生都必须学习代数，必须在“离散数学”和“抽象代数”课程中二选一作为必修课程，如果学生选择学习“抽象代数”，则它们可以在课程312、412或493中任选一门学习。纯粹数学旨在培养学生的严格的逻辑推理能力，并使得学生接触和掌握代数、分析、几何、拓扑等数学分支的精髓。因此，该项目增加了数学的难度，抽象代数是必修课程，学生必须在412和493中任选一门。荣誉数学项目旨在培养学生从事数学科研的能力，为学生今后读数学研究生做好准备。该项目的专业课程由数学系的杰出教师采用小班授课，教学内容涵盖基础数学和应用数学的内容。除了标准课程外，该项目还会讲解算法、密码学、生物数学和金融数学等边缘学科的最新进展。成绩优异的学生可以学习研究生课程。因此，该项目对学生的要求最高，学习的难度最大，抽象代数是必修课程，学生必须学习课程493。

综上所述，密大数学系提供了312、412和493等三个模块的抽象代数课程，学生可根据修课项目的不同选择对应的模块学习。

二、层次性

课程312、412和493都是抽象代数课程，它们有着所有代数类课程的共同目标：让学生接触严谨的代数语言，培养学生严格的逻辑推理能力。但是，由于各自的侧重点不同，所以课程312、412和493所需的基础、开课时间、选取的教材、教学目标、教学内容等都不尽相同。课程312，又名应用近世代数，顾名思义，即侧重培养学生利用抽象代数知识解决实际问题的能力，因此，学生学习的内容有：（1）集合与函数、关系与图、环论、布尔代数、半群、群、格；（2）在开关线路设计、自动化、编码理论等方面的应用。该课程采用的教材是Childs编的《A Concrete Introduction to Higher Algebra》，这本书通过整数和多项式等大家耳熟能详的例子引入环和域等概念，并将一部分环和域的知识通过应用来体现，可读性强，且整本书中有900多个习题。所以，该课程最贴近实际，是这三门课程中难度系数最低的，学生只要学习过线性代数的相关知识就可以学习该课程。课程412与课程312相比，更加重视理论，要求学生掌握抽象代数的基本概念与方法，培养学生较强的逻辑推导能力，学习的内容比课程312更抽象，难度系数更高。课程493是这三门课程中最抽象和最有难度的课程，旨在以严谨的方式向学生介绍群、环、域、模等代数结构，强调概念和证明，讲授的内容几乎是课程412的两倍，讲解的习题非常有挑战性。因此，这三门抽象代数课程在难度上层层递增，有着鲜明的层次性，具体见表1。

三、针对性

在密大数学系，要求学习抽象代数知识的修课项目有数学教学、纯粹数学、荣誉数学（honors mathematics）和数学科学。选择荣誉数学项目的学生基本都会读研究生继续深造，因此需要很强的理论知识，因而他们必须学习难度系数最高的课程493，为他们今后从事科研工作打好坚实的理论基础。纯粹数学项目旨在培养学生严谨的逻辑推理能力和了解数学的各个基本学科，因此必须学习抽象代数课程，但是学生可以根据自己的情况在难度系数有差别的课程412和493中任选一门。数学教学项目要求学生掌握一定的数论知识，因此学生可以根据自己的实际情况选择学习“数论”或“抽象代数”，如果学生选择学习“抽象代数”，则他们可以选择在课程312、412或493中任选一门学习。数学科学项目强调数学的应用性，偏重应用，学生可以选择“离散数学”或“抽象代数”，如果选择了“抽象代数”，他们同样可以在课程312、412或493中任选一门学习。这样的设置方式，充分考虑了学生的学习兴趣和学习能力的差异性，体现了因材施教的教育理念，有着很强的针对性。

区区一门课程却细分成三种选课方案，这些方案在难度上层层递增，兼顾了各个层面的学生，使学生能根据自己的学习能力和学习目的选择合适的方案，充分体现了以学生为本的人文精神，值得我们学习与深思，为我们进行教学改革提供了思路。

参考文献：

[1]乔建永.美国密西根大学教学评估工作的启示[J].中国大学教学，2013，（5）：11-12.

[2]邬大光.世界一流大学解读-以密西根大学为例[J].高等教育研究，2010，（12）：82-93.

[3]吴畏.哲学本科专业的大学定位和人才培养的问题研究——密西根大学安娜堡分校的启示[J].当代教育理论与实践，2013，（5）：57-59.

[4]L.N.Childs.A concrete introduction to higher algebra[M].第三版.Springer，2009.

[5]N.H.McCoy和G.J.Janusz.Introduction to abstract algebra[M].第七版.Trust- worthy Communications， LLC，2009.

[6]Michael Artin.Algebra[M].Pearson Education，2011.endprint