摩擦对水力机组大波动过渡过程影响研究

2016-01-13叶文波王煜于凤荣姜峰余国锋张云

能源研究与信息 2015年2期

叶文波+王煜+于凤荣+姜峰+余国锋+张云龙+蒋百超

摘要：运用MATLAB/Simulink软件对考虑摩擦和不考虑摩擦时一台水力机组在额定工况下甩负荷运行后的大波动过渡过程的仿真结果进行了比较，讨论了摩擦对电站甩负荷后的蜗壳末端水击压力、尾水管末端转速及水轮机真空度等因素的影响，进而为水电站在大波动调保计算时是否考虑摩擦的影响提供一定程度的参考.理论分析表明，摩擦对大波动过渡过程存在一定影响，但是在一定条件下，这种影响可忽略.仿真结果表明，不考虑摩擦时的水击压力和转速都略大于考虑摩擦时的水击压力和转速.对实际工程而言，这种偏大的计算结果是安全的.

关键词：水力机组；摩擦；大波动；仿真；调保计算

中图分类号： TV 136 文献标志码： A

Influence of friction on the large oscillation transient

process of hydraulic unit

YE Wenbo， WANG Yu， YU Fengrong， JIANG Feng， YU Guofeng，

ZHANG Yunlong， JIANG Baichao

（Faculty of Metallurgical and Energy Engineering， Kunming University of

Science and Technology， Kunming 650093， China）

Abstract： Using the MATLAB/Simulink software， the simulation results of large oscillation transient process of one hydraulic unit under the rated condition were compared when the friction was considered or not. The influence of friction on the speed and pressure of hydraulic turbine after load shedding was discussed. The results can provide reference for calculation of regulating guarantee under large oscillation transient process. The theoretical analysis indicates that the friction has some influence on the large oscillation transient process， but this influence can be ignored. The simulation results show that the pressure and speed with no friction are higher than those with the friction， which is safe in terms of projects.

Keywords： hydraulic unit； friction； large oscillation； simulation； calculation of regulating guarantee

水电站过渡过程，尤其是大波动过渡过程，虽然历时短暂，但伴随着工况参数大幅度急剧变化[1].大波动过渡过程的本质是水击波的传播过程[2].在甩负荷时，水轮机流量的急剧变化会引起压力水管末端流量的急剧变化，水管内将出现非恒定流现象，从而使水轮机压力过水系统产生水击，同时由甩负荷引起的转速升高会对机组、厂房的安全造成威胁.调保计算的任务是保证压力和转速的升高不超过允许值.调保计算中所涉及的数学模型、计算过程都会考虑摩擦因素的影响.由摩擦造成的能量消耗使水锤波在管道中的传播不再是一个振幅不变的持续震荡过程，而是一个逐渐衰减趋于消失的过程.由计算水锤的运动方程可知，当水流速度逐渐减小直至趋近于0时，运动方程中的摩擦项对调保计算结果的影响也会越来越小.一般认为在低摩擦阻力的瞬变流中，摩擦阻力对水力瞬变的影响较小，可忽略.[3]压力管道中的摩擦与管径、流体速度以及管道粗糙度等因素密切相关.在流体速度、管道粗糙度相同的情况下，管径越小管道的摩擦系数和水头损失越大，突然停机时水锤波速衰减越快，水锤压力上升幅度越小，摩擦对调保计算的影响也越小[4].另外，在无限长管情况下水击波峰面趋近于原来的水力坡降线，摩擦阻力使管道中的流动最终完全静止，从而水力瞬变亦不再继续.[5]

本文主要研究是否可在特殊工况下不考虑摩擦直接进行调保计算，以简化计算及编程，节省人力、物力.忽略摩擦影响的前提是调保计算结果不会因此产生较大的偏差.本文对考虑摩擦和不考虑摩擦两种情况时水力机组蜗壳末端水击压力、水轮机转速、尾水管末端真空度进行了对比.计算软件为MATLAB/Simulink.

1 计算方法

数学模型可分为四部分：机械旋转运动、有压管道水击、导叶关闭过程和水轮机特性[6].由于在所有的差分方法中特征线法具有可较精确地求解双曲线偏微分方程，并将偏微分方程化为常微分方程等优点，因此比较常用.本文采用特征线法.[7]

式中：S为断面面积，有下标A、B者均为已知量；HA、QA分别为A点的水头和流量；HB、QB分别为B点的水头和流量；HP、QP分别为P点的水头和流量.

求解水力机组过渡过程时，通常从t=0时的定常状态开始.式（5）、（6）中管道的每个计算截面上的HA、QA、HB、QB均已知的，只有两个未知数HP、QP，所以可根据t=0时的压头和流量求出t=Δt时刻的压头和流量，接着计算在t=2Δt时刻的结果，依次类推，一直计算到要求的时间为止[8].

2 理论分析

2.1 隔离体分析

导叶关闭时，取微小的管道为隔离体，由动量定理推导、简化、修正后得

ΔH=-agΔV±Δf

（9）

式中：ΔH为水头变化量；-agΔV为惯性水击压头，ΔV为速度变化量；Δf=FfρSg，Ff为摩擦阻力，Δf前取正负号是因为摩擦力的方向总是和流动方向相反[9].

阀门关闭时，流速由初始时刻的速度V0变为0，ΔV=-V0，压力升高，水流方向和摩擦力方向相反，水击波向上游传播，Δf取负值，此时ΔH=agV0-Δf，摩擦阻力对水击压力的增加起削弱作用.

2.2 具体分析

考虑摩擦时，求解由式（5）、（6）联立的方程组得到P点的水头

HPf=a2gSQA-a2gSQB+12（HB+HA）+

f[QAQP-QBQP]Δx2dSa

（10）

式中：HPf为考虑摩擦时P点的水头.

不考虑摩擦时，有

HP=a2gSQA-a2gSQB+12（HB+HA）

（11）

由式（10）、（11）可得，考虑摩擦和不考虑摩擦的差别为摩擦项F=f[QAQP-QBQP]Δx2dSa.

忽略局部水头损失时，由水力学可知

ΔH=fV2Δx2dg

经假设简化水力半径R=d/4[10]，故f=8gRΔHV2Δx.导叶完全关闭前V=2gH，f=dΔHHΔx；导叶完全关闭后V=2gΔH，f=dΔx

将f代入摩擦项简化得，导叶完全关闭前

F=ξ（QAQP-QBQP）2Sa，ξ=ΔHH

导叶完全关闭后

F=QAQP-QBQP2Sa

过渡过程分析算例中将水轮机作为一个边界条件处理，该边界有上、下游两个节点[11].因为水轮机上游节点的流量QB在导叶关闭过程中大于水轮机下游节点的流量QA，摩擦项是负值，故考虑摩擦时涡壳末端水击压力小于忽略摩擦时涡壳末端水击压力.而在导叶未完全关闭前，随着水锤压力相对值ξ增加，摩擦项对水锤压力的影响会越来越大，这将导致两种情况下的水锤压力差越来越大直至导叶关闭.摩擦项仅由上、下游节点流量差决定，而下游节点流量在导叶关闭后基本不变，上游节点流量也会逐渐趋于稳定，故导叶关闭后考虑摩擦和不考虑摩擦两种情况下的涡壳末端水锤压力差基本稳定在一定值.

3 摩擦对大波动过渡过程的影响3.1 电站概况及调保参数控制要求

本电站为引水式电站，上游设计洪水位为1 237.48 m，下游设计尾水位为1 013.06 m，水库正常蓄水位为1 240 m，运行死水位为1 166 m.水轮机型号为HL153-LJ-660，电站额定水头为221 m，额定流量为348.4 m3，额定出力为714 MW，机组转动惯量为110 000 t·m2.蜗壳末端最大动水压力不超过2.6 MPa（265.8 m水柱）；尾水锥管内的最大真空度不得大于7 m水柱；最高转速上升值不大于额定转速的50%.

3.2 摩擦对大波动过渡过程影响的对比分析

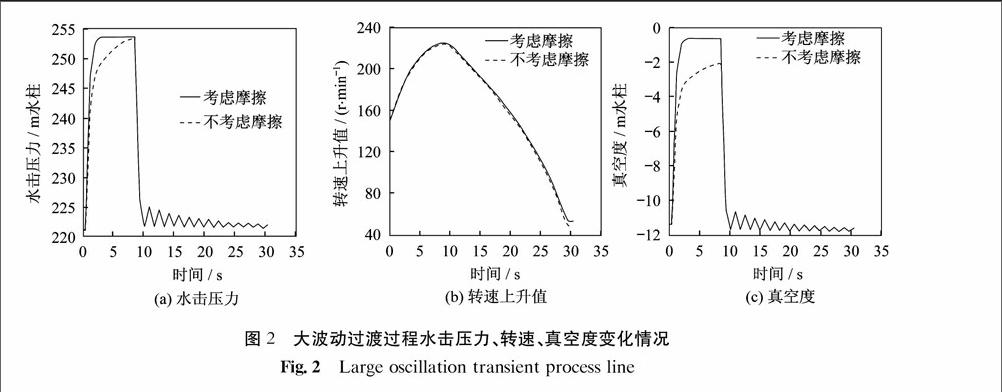
导叶关闭规律采用直线关闭，关闭时间为9 s.当机组在额定转速、额定水头、额定出力运行甩负荷时，大波动过渡过程水击压力、转速、真空度变化情况如图2所示.

由图2分析可知：

（1）考虑摩擦和不考虑摩擦时蜗壳末端最大水击压力分别为253.3、253.4 m水柱，小于允许值265.8 m水柱，发生时间分别为导叶关闭后8.5、3.6 s.8.5 s前不考虑摩擦时的水击压力一直高于考虑摩擦时的水击压力，9 s后两种情况下的压力都开始衰减，不同的是不考虑摩擦时衰减的幅度更大.

图2 大波动过渡过程水击压力、转速、真空度变化情况

Fig.2 Large oscillation transient process line

（2）考虑摩擦比不考虑摩擦时转速上升百分比低0.6%；考虑摩擦和不考虑摩擦时最大转速上升值分别为223.8、225.1 r·min-1，两者均小于最大转速上升允许值，发生时间均为导叶关闭后9.3 s.

（3）考虑摩擦与不考虑摩擦时尾水管进口最大进口真空度相差1.45 m水柱；考虑摩擦和不考虑摩擦时尾水管进口真空度分别为-2.10、-0.65 m水柱，均小于允许值7 m水柱，发生时间分别为导叶关闭后3.6、8.5 s.8.5 s后两条曲线开始衰减并震荡，其规律和完全关闭导叶后蜗壳末端水击压力升高曲线相同.

（4）蜗壳末端水击压力变化曲线和尾水管进口真空度变化曲线变化趋势相近.在导叶完全关闭前，不考虑摩擦时蜗壳末端水击压力和尾水管进口真空度均大于考虑摩擦时的相应值.这是因为摩擦阻力对水击增压过程起抑制作用，并与理论分析相吻合；导叶关闭前，摩擦对流量的影响随着水击压力的增大而增大，所以是否考虑摩擦会影响到蜗壳末端水击压力，进而影响尾水管进口真空度和机组转速上升值.当导叶完全关闭后，摩擦阻力将促进水击压力衰减，故其压力衰减较快.另外，蜗壳和尾水管中的流速只和水头变化量有关而与水头无关，摩擦对蜗壳末端水击压力仍存在影响，且两者的差值基本维持恒定，具体体现为导叶完全关闭后不考虑摩擦时的水击压力仍高于考虑摩擦时的水击压力，且其衰减幅度要高于后者.这一方面是由于摩擦和流量密不可分的关系对导叶关闭后的水击压力产生了影响；另一方面也与摩擦的存在造成了能量的消耗有关.

（5）转速变化曲线与水击压力、真空度两种曲线变化有所不同.考虑摩擦时转速基本上一直低于不考虑摩擦时的转速，其原因是在导叶完全关闭前后，考虑摩擦时的水击压力上升小于不考虑摩擦时的水锤压力上升，进而导致前者压力上升对转速上升的影响小于后者.

4 结语

由计算结果和分析可知，不考虑摩擦时蜗壳末端水击压力与水轮机转速等参数较考虑摩擦时大些.对于实际工程而言，计算结果偏大是安全的，故一般情况下不考虑摩擦可简化计算且满足工程要求.

本文计算适当做了一些近似处理，忽略了引水管道中局部损失系数的影响，而且导叶关闭规律只考虑直线关闭，未对各种水头下的两种情况进行对比分析.这些因素都会导致计算结果和实际电站运行参数有一些出入.但是从运动方程理论分析上考虑，研究结果仍具有一定的通用性和实际指导价值.

参考文献：

[1] 何文学，李荼清.水电站大波动过渡过程研究现状及发展趋势[J].水利水电科技进展，2003，23（14）：58-59.

[2] 沈祖诒.水轮机调节[M].北京：中国水利水电出版社，2008.

[3] 刘刚，蒲家宁.瞬变流摩阻计算及摩阻对水力瞬变的影响[J].力学与实践，2003，25（1）：13-15.

[4] 程鹏.摩阻对长距离输水管道水力过渡过程的影响研究[D].西安：长安大学，2012.

[5] WYLIE E B，STREET V L.Fluid Transients[M].Michigan：Feb Press，1983.

[6] 杨剑锋.水力机械过渡过程计算研究[D].武汉：华中科技大学，2011.

[7] 郑源，张健.水力机组的过渡过程[M].北京：北京大学出版社，2008.