基于冲突概率的无信号控制T形交叉口安全评价

基于冲突概率的无信号控制T形交叉口安全评价*

张小秀1杨晓光1▲赵靖2

(1.同济大学交通运输工程学院上海201804；2.上海理工大学管理学院上海200093)

摘要为了更合理地评价无信号控制T形交叉口的安全水平，研究在交叉口类型划分的基础上，提出1种以交通冲突数的概率分布为评价指标的安全评价方法。其中，交通冲突数的均值和分布分别采用广义线形模型和泊松分布描述，在广义线形模型中，交通冲突数的均值为被解释变量，冲突交通流的交通量为解释变量，根据交通冲突数的均值估算，计算交通冲突数的泊松分布的概率。在利用实测数据对广义线形模型的参数进行标定后，根据主路直行与非直行交通流量之间的差异性，进一步提出了简化模型，将主路直行交通的影响简化为影响系数，并根据流量不同划分为4个等级，通过分析交通冲突数的概率计算值与安全阈值数的概率临界值之间的关系，进行无信号控制T形交叉口的安全评价。最后通过实际案例，对模型的可操作性和准确性进行了检验。研究表明，非直行流向流量较直行交通流量对交叉口安全水平的影响更大，利用文中所提出的简化模型，可重点调查其它流向流量，而主路直行交通流量只需观测其流量大致范围即可，平均工作效率提升25%。

关键词交通安全；安全评价；无信号控制T形交叉口；冲突概率；回归分析

中图分类号：U491.2文献标志码：A

收稿日期：2015-04-28修回日期：2015-07-13

基金项目*国家自然科学基金重点项目(批准号：51238008)、上海理工大学博士启动(批准号：BSQD201504)资助

作者简介：第一张小秀(1973-)，硕士研究生，高级工程师.研究方向：交通安全与系统设计.E-mail：392316175@qq.com

A Safety Evaluation Model for Unsignalized

T-Intersections Based on Conflict Probability

ZHANG Xiaoxiu1YANG Xiaoguang1ZHAO Jing2

(1.SchoolofTransportationEngineering,TongjiUniversity,Shanghai201804 ,China;

2.BusinessSchool,UniversityofShanghaiforScienceandTechnology,Shanghai200093 ,China)

Abstract:In order to evaluating the safety of the unsignalized T-intersections in a more objective way, this paper proposes a safety evaluation method after providing a detailed classification of intersections. The probability of traffic conflicts is used as the evaluation index. In this paper, the average of traffic conflicts and its probability are described using a generalized linear model and Poisson distribution. In the generalized linear model, the average of the traffic conflicts is used as the explained variable while the conflict traffic flow rate as an explanatory variable. The traffic conflict probability of Poisson distribution is estimated based on the estimated average of conflict traffic. A simplified model is developed after the model parameters are calibrated based on the survey data. The effect of the through movements on main-street is simplified by an impact factor, which is divided into 4 levels based on the volumes. By analyzing the relationship between the calculated value of traffic conflict probability and the critical value of safety probability threshold, the safety of the unsignalized T-intersections is evaluated. The feasibility and accuracy of the model is validated through actual cases. The results show that the traffic volumes of the turning movements have a greater effect on the safety than through movements. The study concludes that the volume of turning movements should be more carefully investigated than the volume of the through movements on main-road when using the proposed simplified model. The efficiency can be improved by 25% in average.

Key words:traffic safety；safety evaluation；unsignalized t-intersections；conflict probability；regression analysis

▲通信作者：杨晓光(1959-)，教授、博导.研究方向：复杂交通运输系统分析与优化设计及管理与控制理论和技术.E-mail：yangxg@mail.tongji.edu.cn

0引言

交通安全问题因其负面影响力大，长期以来是交通发展中不可忽视的问题。根据2013年世界卫生组织道路安全全球现状报告，每年约有130万人因道路交通伤害而死亡。若不采取措施，预计2030年，车祸将成为第五大死亡原因[1]。因此，有必要对交通设施进行安全评价。

无信号控制交叉口作为道路的连接点，交通流向众多，运行复杂。虽然从法律意义上有明确的通行权优先级定义，但在我国目前的管理水平下，驾驶人往往会出于减少等待时间的目的，忽略路权的优先次序，导致交通事故频发[2]。本研究针对无信号控制T形交叉口，在将交叉口进行分类的基础上，提出了1种以交通冲突数的概率分布为评价指标的安全评价方法。该方法的交通冲突数的均值和分布分别采用广义线形模型和泊松分布描述，考虑了2股冲突交通流的交通量，同时，进一步考虑到无信号控制T形交叉口直行交通流量与非直行交通流量之间的差异性，将主路直行交通的影响简化为影响系数，并根据其流量不同划分为4个等级，这种简化方法一方面可以避免对主要交流量进行全部调查，增加调查工作，另一方面仅在调查次要交通流量基础上，快速进行安全评价。

1相关研究综述

目前关于交叉口交通安全评价的方法主要包括以下3类。

1)基于交通事故的安全评价方法。主要包括绝对指标、相对指标、综合指标[3]。绝对指标是反映道路交通事故状况的基本指标，通常被称为4大指标的是：事故次数、死亡人数、受伤人数、直接经济损失，绝对指标是其他评价指标的计量基础。相对指标中，人们引入了车辆保有量、交通量、人口或区域面积等因素作为比较的基础，相对指标分为结构相对数、比较相对数、强度相对数、动态相对数，利用这些指标可以深入地认识交通事故的发展变化程度、内部结构、对比情况、事故强度等[4-5]。该评价方法被认为是最直接、最根本的方法，但存在着事故数据样本收集周期过长、不准确、无法揭示交通参与者对交通事故的影响等问题。

2)基于交通冲突的安全评价。以冲突数或冲突率为指标对采集到的冲突数据进行分析处理，进而对考察对象的交通安全状况进行定量描述，主要包括：冲突数、冲突率、综合交通冲突率。以冲突数为指标，通过比较一定观测时段内不同交叉口的绝对冲突数，得出交叉口交通安全状况的优劣顺序；以冲突率为指标，即考虑冲突数的影响，又考虑交通量的因素，通过小时冲突数与小时当量交通量的比值的大小，对交叉口交通安全状况进行评价[6]；综合交通冲突率在冲突率指标的基础上，将不同冲突类型进行加权，得到评价设施安全水平的综合指标。该评价方法有短时间内可获取数据并可进行评价、交通冲突中包含了人的因素等优点[7-8]。

3)基于速度一致性的安全评价。基于速度的安全评价指标多运用于路段的安全评价，通过计算单车在道路各断面的速度差、各断面运行速度差、运行车速与设计速度差值等指标，对速度一致性进行评价[9-10〗。

以上3种方法各有优劣，针对本文所研究的T形交叉口，第1、第2种方法均可使用。考虑到数据采集的可行性及准确性，交通冲突相对于事故数据更普遍且更易获取，有利于增强模型的可移植性，国内研究多基于交通冲突进行安全评价，并对冲突点数[11]和冲突大小指标[12]进行了研究。本研究将在此基础上，进一步对无信号控制T形交叉口安全水平进行建模，并基于实测数据对模型参数进行了标定。

2模型建立

研究将从评价对象分类、评价指标计算和安全水平判别3个部分展开，建立无信号控制T形交叉口安全评价模型。

2.1评价对象分类

道路交通冲突发生数量具有离散、整数的特点，一般情况下，单位时间内交通冲突发生的次数符合泊松分布。但当交通冲突数据过度离散，即样本的均数与方差不相等时，泊松分布可能就不再适用[10, 13]。因此，本文引入交叉口类(或簇)的概念，将交叉口划分为若干具有共同属性与特征的类别，分别进行研究，以控制冲突数据的离散程度，保障回归分析的精度。针对本文所研究的无信号控制T形交叉口，具体分类原则及代号如下。

1)按交叉口所在区域，分为城市(U)和乡村(R)。

2)按交叉口主路车道数，分为主路双向2车道(2)和主路双向4车道(4)。

按照上述分类原则对交叉口的类别进行编号，如：U4，U2，R2分别代表城市主路4车道、城市主路2车道、乡村主路2车道交叉口类，符合这些条件的交叉口类都有共同的属性。后文将以交叉口类为对象确定单位时间内交通冲突发生次数的期望值，交叉口类的每1个交叉口的交通冲突进行安全评价。

2.2评价指标计算

本研究采用交通冲突对无信号控制T形交叉口安全水平进行评价，根据无信号控制T形交叉口各流向的路权等级，将交通冲突界定如下。

1)低等级路权车辆或大于等于2辆车同时减速或排队让行高等级路权车辆，视为1次冲突。

2)低等级路权车辆在减速或停车让过程中，影响其他流向车辆正常通行时，记为1次交通冲突。

3)低等级路权车辆利用高等级路权车辆间隙穿越，引起高等级路权车辆减速或排队，视为1次冲突。

4)车辆让行行人或行人让行车辆均记为1次交通冲突。

就无信号控制T形交叉口而言，交通冲突的严重程度并不意味着绝对交通冲突数就大，且相关冲突交通流之间的交通流量或相差较大，或相当，因此，采用交通冲突发生的概率对交叉口进行安全评价，则比较合理。

建立交通冲突估计模型，计算单位时间内交通冲突发生次数的均值。对于交通冲突模型的基本形式，本研究借鉴交通事故预测模型的研究成果，采用广义线性函数表述[10]。这是由于一方面，已有的交通流量与交通事故预测模型是经典的模型形式，同时该模型形式是传统的线性模型的延伸，以往交通事故预测研究结果表明广义线性函数能够反映传统的线性回归模型难以描述事故发生的随机性、离散性和非负性特性[14-16]。另一方面，Migletz[17]和刘小明[18]的研究均指出交通冲突与交通事故发生规律具有相似性，借鉴交通事故预测模型的基本形式进行交通冲突的计算具有可行性。经过数据的拟合结果证明，交通事故模型形式也适合于交通冲突对交通流量的关系描述。单位时间内交通冲突数均值的广义线形模型为：

(1)

式中：Ci为发生在交叉口类i观测时段内的交通冲突平均次数；V1i为发生交通冲突相关交通流量，veh/h；V2i为发生交通冲突相关交通流量，veh/h；β0，β1，β2为模型参数。

计算每个交叉口在单位时间内观测到发生y次交通冲突的概率P，P(Y=y)值用泊松分布的概率表示

(2)

式中：P为交叉口发生的概率；Ci为发生在交叉口类i观测时段内的交通冲突次数的平均值；y为交叉口交通冲突发生次数。

对每个交叉口而言，根据交叉口类在单位时间内交通冲突发生的平均值，计算交通冲突次数大于或小于交通冲突次数安全阈值的概率，P(Y≤y)和P(Y≥y)值分别为

(3)

(4)

2.3安全水平判别

设定α为交叉口交通冲突概率安全水平值，P(Y≤N)或P(Y≥N)=α，α为交通冲突概率安全水平值，N为交通冲突次数安全阈值。

对于P(Y≤N)情况见图1(a)，交通冲突次数小于N次的概率随着交通冲突发生y次数的减小而逐渐减小。当交叉口类中任一交叉口的交通冲突概率P(Y≤N)<α，也就是意味着，该交叉口交通冲突概率预测值小于交通冲突概率安全水平值时，对应的交通冲突发生的次数小于交通冲突次数安全阈值，则交叉口处于安全水平；

对于P(Y≥N)情况见图1(b)，交通冲突次数大于N次的概率随着交通冲突发生y次数的增加而逐渐减小。当交叉口类中任一交叉口的交通冲突概率P(Y≥N)<α，也就意味着，当该交叉口交通冲突概率预测值小于交通冲突概率安全水平值时，对应的交通冲突发生的次数大于交通冲突次数安全阈值，则交叉口处于不安全水平，同时，P(Y≥N)>α时，对应的交通冲突发生的次数小于交通冲突次数安全阈值，交叉口处于安全水平。

综上所述，笔者采用交通冲突数的概率分布作为评价指标，对无信号控制T形交叉口进行安全评价，具体为

当P(y≤N)<α或P(y≥N)>α,交叉口安全；当P(y≥N)<α，交叉口不安全

(5)

式中：α为设定交通冲突概率安全水平值；N为交通冲突次数安全阈值。

图1　冲突概率与安全分析 Fig.1　Analysis of conflict probability and safety

3参数估计

选取宁波市长春路与马衙街支路、中山西路与天一家园支路、联丰路与联南社区支路、薛家南路与西城支路4个无信号控制T形控制交叉口，进行交通冲突调查见图2，这4个交叉口按类型划分均属于U4类交叉口。采用视频录像的方法对上述4个交叉口进行冲突调查。调查时段为上午07：00～09：00时，下午17：00～18：00时，连续观测5d。

图2　交叉口交通冲突调查 Fig.2　The investigation of traffic conflict at intersections

以15min，1h或1d的交通流量建立的模型无太大的差别[19]，本文以15min为间隔，对交通量和交通冲突数进行统计。运用SAS9.2软件模型进行回归方差分析、模型决定系数与回归系数分析，见表1～表4。在模型参数估计的结果中，直行交通流量和其它流向流量对应变量的统计量p值分别为0.081(>0.05)和<0.0001，运用pearson相关系数进一步，对上述直行交通流量和其他流向流量与冲突数相关性分析，显示两者均与冲突数线性相关。因此，将这2个变量纳入回归模型是合适的，见表1、表2。

表1　交通冲突模型参数

表2　冲突模型变量相关性分析

建立多元回归模型后，检验回归模型整体显著性水平见表3，将观测值计算F统计量的p值与显著水平α比较，结果显示p<0.0001，可认为该模型回归方程是显著的。且模型的决定系数分析也显示模型的回归效果较好见表4。模型残差图见图3，数据点对称地紧密分布在横轴附近，且没有任何确定的趋势。

表3　交通冲突模型回归方差分析

表4　交通冲突模型决定系数和回归系数分析

图3　模型残差图 Fig.3　The residuals of the model

从表1～表4以及模型的残差图可得出，建立的直行与其他流向的冲突模型是合理的，单位时间内交通冲突均值模型为

(6)

对于无信号控制T形交叉口，通常主路直行的交通流量远远大于其他与之相冲突流向的交通流量，且流量相对稳定，进行交叉口交通冲突调查时，主路直行交通量不需专门调查，可根据与该交叉口的相邻信号交叉口获取，仅只需要获取与主路直行冲突的其它流向流量即可，因此，对该类型交叉口交通冲突次数模型进行简化。为方便模型计算与简化，可根据主路直行交通量的划分范围，对模型简化为

(7)

式中：φ为主路直行车辆交通量影响系数，与主路直行交通量的大小有关。当V1=400～500pcu/h，φ取6；当V1=600～900pcu/h，φ取7；当V1=1000～1400pcu/h，φ取8；当V1=1500～2100pcu/h，φ取9。

4实例验证

为了检验上述交通冲突次数简化模型，又对蓝天路与丽园馨都支路、联丰中路与都市港湾支路、联丰路与169弄支路、兴宁路与黄鹂新村支路交叉口进行了调查，调查时长均为2h。调查中主要对与主路直行冲突的其他流向流量和交通冲突次数进行了统计，各交叉口小时冲突数预测值与实际观测值以及相对误差见表5。

总体上，简化模型的平均误差为19.4%，与以往冲突数预测模型平均误差(约15.8%[20])相差不大，但对于无信号控制T形交叉口而言，其直行交通流量占交叉口总的冲突交通流的比例约80%以上，因此，在此条件下，本研究模型可显著减少实际调查工作量，平均工作效率可提升25%，具有较好的应用价值。通过表5可以看出，总的来说，交通冲突均值估算模型预测结果一般情况下会大于实际观测值，这主要是由于不同路权分配等级的交通流，在停让时交通冲突点之间相互作用的影响造成的。在实测检验的4个T形交叉口中，在其中2个T形交叉口预测模型表现较好，但在蓝天路与丽园馨都支路交叉口和兴宁路与黄鹂新村支路交叉口模型表现不十分理想，误差达到了25%左右。进一步分析发现，这2个无信号控制T形交叉口与下游信号控制交叉口间距较短，导致车辆到达受信号灯影响显著，车流到达更为集中。根据本文中冲突观测的界定规则1，低等级路权车辆或大于等于2辆车同时减速或排队让行高等级路权车辆视为1次冲突，同时也受交通冲突点之间的相互作用的影响，因此，观测统计的冲突数明显少于模型预测值。这反映出模型可能不适用于无信号控制T形交叉口距离信号控制交叉口距离较近的情况。

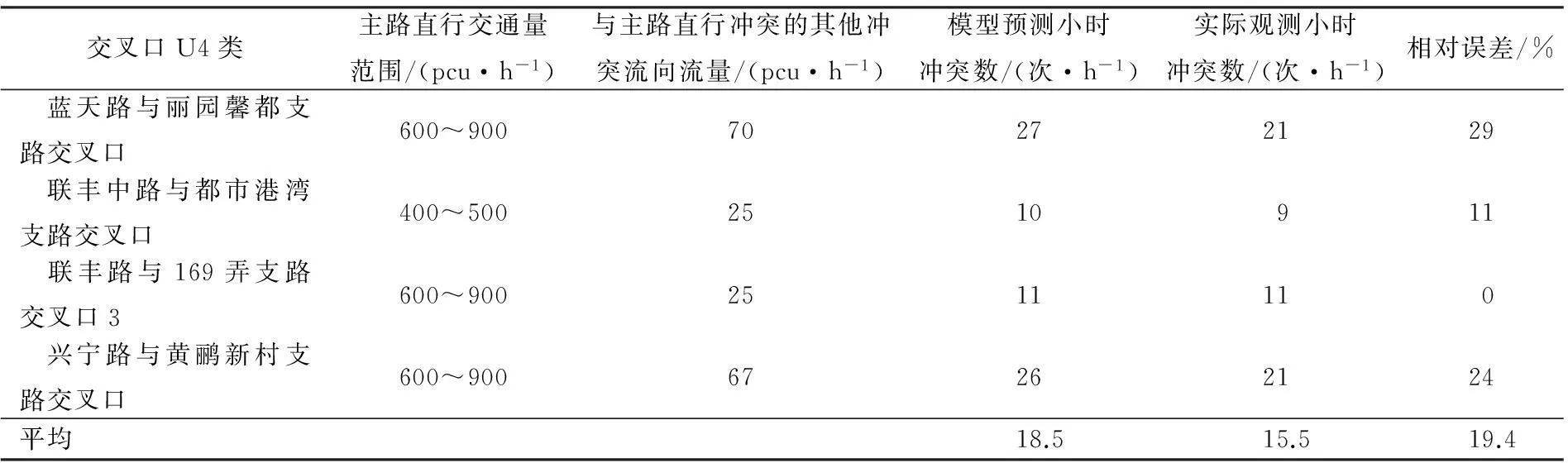
表5　交通冲突模型观测值与预测值及相对误差

进一步计算P(Y≥y)和P(Y≤y)值见表6。设定交叉口类的交通冲突概率安全水平值，α=0.05，对照表6，P(Y≥N)<α=0.05和P(Y≤N)<α=0.05，然后可对这4个交叉口进行了安全评价。

蓝天路与丽园馨都支路交叉口交通冲突的实测值为9次/h，P(y≤9)=0.0089<α，处于安全状态；联丰中路与都市港湾支路交叉口交通冲突的实测值为10次/h，P(y≤10)=0.018<α，处于安全状态；联丰路与169弄支路交叉口交通冲突的实测值为21次/h，P(y≥21)=0.3528，实际交通冲突次数未超过交通冲突>P(Y≥N)<α=0.05，处于安全状态；兴宁路与黄鹂新村支路交叉口交通冲突的实测值为27次/h，P(y≥27)=0.048<α=0.05，交叉口处于不安全状态，需通过设计或管理组织手段等方式减少交通冲突。

表6　交通冲突概率临界值

5结束语

本文针对无信号控制T形交叉口，在提出交叉口类的基础上，分别采用广义线形模型和泊松分布模型确定了交通冲突数的均值和分布。在利用实测数据对广义线形模型的参数进行标定后，进一步提出了简化模型。该简化模型通过影响系数来简化反应主路直行交通量对安全的影响，影响系数则根据流量大小划分为了4个等级，通过分析交通冲突数的概率计算值与安全阈值数的概率临界值之间的关系，进行无信号控制T形交叉口的安全评价。经模型的简化，显著减少了实际应用中的调查工作量，平均工作效率可提升25%。论文最后利用实际案例，对模型的可操作性和准确性进行了检验。研究表明：

1)所建立的安全评价模型与实际观测数据的拟合程度较好，与实测数据相比，简化模型可将误差控制在30%以内。误差主要来源于两个模型检验点距离信号控制交叉口较近，车流到达分布与模型标定时的情况差异较大。

2)对于无信号控制T形交叉口，非主流向(直行)流量较直行交通流量对交叉口安全水平的影响更大。

3)在实际应用中，考虑到主路直行交通流量通常远远大于其他与之相冲突流向的交通流量，且相对稳定，调查中可重点观测其它流向流量，而主路直行交通流量只需观测其流量大致范围即可，由此可大大减少调查工作量。

本研究将无信号控制T形交叉口作为1个独立的对象进行研究，未考虑路网中其它交叉口的影响。因此所建立的模型不适用于无信号控制T形交叉口距离信号控制交叉口距离较近的情况。下一步研究中，一方面应就交叉口所在区域及车道数的不同，分别进行参数标定，以形成1个完整的无信号控制T形交叉口安全评价体系；另一方面，应研究交通流到达分布的影响，以适应其运行受路网中其它交叉口影响的情况。

参考文献

[1] 世界卫生组织．道路安全全球现状报告[R].瑞士，日内瓦：世界卫生组织．2013.

World Health Organization．Global status report on road safety[R].Switzerland,Geneva: World Health Organization．2013.

[2]成卫. 城市交通冲突技术理论与应用[M]. 北京：科学出版社,2006.

CHENG Wei.Theory and Application of Urban Traffic Conflict Technique [M]. Beijing: Science Press, 2006. (in Chinese)

[3]沈斐敏. 道路交通安全[M]. 北京：机械工业出版社，2008.

SHEN Feimin. Road traffic safety[M].Beijing: China Machine Press, 2008.(in Chinese)

[4]曲麟智. 城市信号交叉口安全评价研究[D]. 北京：北京邮电大学，2011.

QU Linzhi. Analysis on safety of urban signalized intersection[D]. Beijing: Beijing University of Posts and Telecommunications, 2011. (in Chinese)

[5]刘耀辉. 基于TCT公路平交口安全评价及改善[D]. 西安：长安大学，2010.

LIU Yaohui. Road intersection safety evaluation and improvement based on traffic technique[D]. Xi′an: Chang′an University, 2010. (in Chinese)

[6]项乔君，陆键，卢川，等. 道路交通冲突分析技术及应用[M]. 北京：科学出版社，2008.

XIANG Qiaojun, LU Jian, LU Chuan, et al. Analysis and application of road traffic conflict technique[M]. Beijing: Science Press, 2008. (in Chinese)

[7]袁黎，袁荷伟，项乔君，等. 基于交通冲突分析的公路信号交叉口安全评价[J]. 交通信息与安全，2010，28(1): 117-120.

YUAN Li, YUAN Hewei, XIANG Qiaojun, et al. Safety evaluation of signalized intersection using traffic conflict technique[J]. Journal of Transport Information and Safety, 2010，28(1): 117-120. (in Chinese)

[8]KIRK, ADAM, STAMATIADIS, et al. Development of intersection safety exposure estimates Through Conflict Models[C]. Transportation Research Board 91st Annual Meeting. Washington, DC: Transportation Research Board, 2012.

[9]郭唐仪，邓卫，LU John. 基于速度一致性的高速公路出口安全评价[J]. 交通运输系统工程与信息，2010，10(6): 76-81.

GUO Tangyi, DENG Wei, LU John. Safety evaluation for freeway exit ram based on speed consistency[J]. Journal of Transportation Systems Engineering and Information Technology, 2010，10(6): 76-81. (in Chinese)

[10] 唐琤琤，张铁军，何勇，等. 道路交通安全评价[M]. 北京：人民交通出版社，2008.

TANG Chengcheng, ZHANG Tiejun, HE Yong, et al. Road traffic safety evaluation[M]. Beijing: China Communication Press, 2008. (in Chinese)

[11]潘福全，张丽霞，陆键，等. 无信号平面交叉口机动车冲突点数计算模型[J]. 上海交通大学学报，2013，47(2): 259-263.

PAN Fuquan, ZHANG Lixia, LU Jian, et al. Calculation models of conflict points for motorized vehcles at unsignalized intersections[J]. Journal of Shanghai Jiaotong University, 2013,47(2): 259-263. (in Chinese)

[12]陈凯. 基于T形道路交通安全冲突评价指标研究[J]. 交通科技，2007(1): 93-95.

CHEN Kai. Establishment of Traffic Conflict Index[J].Transportation Science&Technology, 2007(1): 93-95. (in Chinese)

[13]赵永红，白玉，杨晓光. 基于Poisson过程的交通冲突预测模型研究[J]. 交通信息与安全，2011，29(1): 8-11.

ZHAO Yonghong, BAI Yu, YANG Xiaoguang, Stochastic process-based traffic conflict predicting model[J]. Journal of Transport Information and Safety, 2011，29(1): 8-11. (in Chinese)

[14]黄靖南. 台湾区中同高速公路肇事分析与预测模式之研究[D]. 台湾：国立交通大学，1984.

HUANG Jingnan. Analysis on Zhongtong highway accident of Taiwan region and study on prediction mode [D]. Taiwan: National Chiao Tung University, 1984. (in Chinese)

[15]刘小明，任福田，朱弘戈. 基于数量化理论的高速公路交通事故预测方法[J]. 道路交通与安全，2001(1)：18-24.

LIU Xiaoming, REN Futian,ZHU Hongge. Highway traffic accident forecasting methods based on quantification theory[J]. Road Traffic & Safety, 2001(1):18-24. (in Chinese)

[16]秦利燕，许洪国. 基于量化理论的高速公路交通安全评价模型[J]. 山东交通学院学报，2002，10(4)：33-36.

QIN Liyan, XU Hongguo. Traffic safety evaluation model of super highway based on quantification theory[J]. Journal of Shandong Jiaotong University, 2002, 10(4):33-36. (in Chinese)

[17]MIGLETZ, D.J.,GLAUZ, W.D,BAUER, K.M. Relationships between traffic conflicts and accidents. Report No: FHWA/RD-84/042[R].Washington D.C.:US Department of Transportation, Highway Administration,1985.

[18]刘小明，段海林. 平面交叉口交通冲突概率分布模型及安全评价标准研究[J].交通工程，1997，23(3)：44-50.

LIU Xiaoming，DUAN Hailin.Research on traffic conflict probability distribution model and safety evaluation standard at intersections[J].Traffic Engineering, 1997，23(3)：44-50.(in Chinese)

[19]MIAOU S P, LUM H. Modeling vehicle accidents and highway geometric design relationships[J]. Accident Analysis ﹠ Prevention, 1993,25(6):689-709.

[20]陈曦. 基于交通冲突定量分析的交叉口危险度模型研究[D]. 北京：北京交通大学，2012.

CHEN Xi. Research on the intersection risk degree model based on traffic conflict quantitative analysis [D].Beijing: Beijing Jiaotong University, 2012. (in Chinese)