具有Holing-Ⅱ反应函数的一类捕食系统的动态分析
2016-01-12张翼,赵飞
张 翼, 赵 飞
(1.沈阳工业大学 理学院, 辽宁 沈阳 110870; 2. 南京理工大学 自动化学院, 江苏 南京 210094)
捕食者与食饵的相互作用关系很复杂,这种关系需要经历长期的协同进化逐步形成,而不是一朝一夕得来的.捕食者固然有一整套适应性特征,以便顺利地捕食食饵,但是食饵也会相应地产生一系列适应性的特征,以逃避捕食者的捕食,这些特征是多方面的.总之,食饵种群通过建立庇护所空间以达到躲避被捕食者捕食的目的.
庇护所保护下的食饵-捕食者模型是一个很热门的话题,近年来受到越来越多学者的关注与研究.庇护所保护下的食饵-捕食者模型已经得到了一些经验和理论,如考虑相互干扰与食饵灭绝的性质时得出了:在庇护所保护下的食饵可以达到稳定的效果[1-5].文献[4]提出:食饵庇护所对捕食者和食饵两物种的持续性属性没有影响,但可能对食饵和捕食者两种群密度的影响很大.
Hassell[6]提出食肉动物物种间相互干涉的概念,并介绍了相互干扰常数,这使得相互干扰的食饵-捕食者模型的研究在物种的动力分析等方面成为一个重要的研究课题.在文献[7]中,作者得出了在系数不受任何约束且物种相互干扰作用下,具有Holing-Ⅱ反应函数的Lotka-Volterra模型总有一个正周期解.而对于一般的不受互相干扰影响的食饵-捕食者模型,为了确保正周期解的存在性,须对模型的系数进行约束限制.
庇护所效应对于种群增长的影响由两部分组成.第一部分称之为初始效应,即食饵种群死亡率的下降.食饵为了躲避捕食者的捕食进入庇护空间,使得能够被捕食者捕食的食饵数量减少,从而降低了食饵种群的死亡率.但是,由于捕食者能够捕食导致食饵数量的下降,致使捕食者面临被饿死的风险,这对捕食者来说是极其不利的.由此可见,庇护所效应的初始效应对食饵种群产生了正面效应,而对捕食者产生了负面效应.然而,由于庇护所空间中生存环境相对恶劣,必然导致食饵种群的出生率降低,这就是庇护所效应的第二效应.Taylor将庇护所分为两类:一类是保护一定比例的食饵,如寄生者攻击粉娥毛虫时,只能将产卵管刺入一定深度的粉娥培养基中,因此,那些处于培养基深处的粉娥毛虫将逃过被寄生的可能性,保护了一定比例的粉娥毛虫;另一类是保护固定数量的食饵,如捕食者娥螺大多数都是在较低地区捕食藤壶的幼体,因为较高地区的藤壶幼体都暴露在空气中,使得较高地区的藤壶幼体只能在海水短暂地、高潮位被捕食,这样较高地区的藤壶幼体逃脱了被捕食的可能,则较高地区成为了一个能够保护固定食饵数量的庇护所.T. K. Kar在文献[3]中介绍了如下模型:


(1)

已经有大量学者对具有庇护所保护作用的食饵-捕食者模型进行了研究,讨论了庇护所效应对生物种群的影响并且得出了一些结论.但在实际情况中,庇护所空间相对较小、生存环境相对恶劣、食物资源相对匮乏等,使得被保护起来的食饵具有死亡率.以前的大量论文只考虑了庇护所对种群的影响,却没有考虑到被保护的食饵的死亡率问题.本文考虑了被保护的食饵的死亡率与种内、种间干扰等情况,对具有Holing-Ⅱ功能反应函数的庇护所效应进行了分析论证,使模型更具有实际意义.
1 模型的建立
首先建立下面的食饵-捕食者模型:
(2)

其次将要深入研究下面的食饵-捕食者模型:
(3)
其中xR=qx,并且0 本文给出了模型的解有界的条件;当食饵在庇护所保护下,对种间干扰的影响进行了分析;最后,通过数值模拟说明了所给结论的有效性. 定理1若模型(3)中x(t)、y(t)有正解,则模型的解有界. 证明: 考虑解x(t)、y(t)在Ω0范围内,模型(3)有正解.定义函数w(x,y)=cx+y,对于任何ε>0,x(t)≤k+ε,有: 因为m1,m2,m3>0,且0 -min{γ,α}w+2cα(k+ε) 有界性得证. 这个模型有3个平衡点,由定理1可知: (ii)L1捕食者等斜线 对于所有x>0,y>0,γ>c有: (iii)L3是食饵等斜线 +∞. n(qx*)=0, 图1 模型(3)的平衡点E*(x*,y*) 证明:模型(3)的雅可比行列式为: 且 那么E*(x*,y*)是局部渐近稳定的.反之,平衡点E*(x*,y*)是不稳定的.证毕. 若两种群都受密度制约,并且平衡点E*(x*,y*)是局部渐近稳定,则平衡点E*(x*,y*)是全局稳定[8]. 由文献[3]可知:如果正平衡点存在且不稳定,则至少存在一个极限环.下面主要研究模型只受捕食者对食饵的种间干扰,即在模型(3)中,若m2=m3=1,考虑下列模型: (4) 把模型(4)改写成如下形式的模型: (5) 根据上面模型(5)的变形,证明模型(5)有唯一极限环.因为模型(5)是模型(4)的变形,所以模型(4)也有唯一极限环. 在模型(5)中 0≤x 模型(5)存在一个极限环[9].因为模型(5)是模型(4)的变形,所以模型(4)也有唯一极限环. 证明: 其中, 证毕. m1=logxcm3[1+a(1-q)x]ym3-1, 在经过这一点时,平衡点的稳定性丧失,变成不稳定的,而产生的极限环变成稳定的. 为了保证虾和贝类的可持续生存,我国渔业每年都有捕捞休整期,而捕捞休整期就是人为的为虾和贝类等动物建立的庇护所. 在以上情况下提取数据并进一步结合2011中国渔业统计年鉴[10]的数据,可以得到下面的参数值: m=1.2,α=10,k=100,β=0.6,a=0.02, b=0.01,c=0.02,n=0.01,γ=0.09 根据得到的参数,模型(3)取q=0.5时,对模型进行了数值仿真,结果见图2、图3. 图2 模型(3)的局部稳定性 图3 模型(3)的全局稳定性 图2、图3表明:当模型(3)有正解,且解有界时,若E*(x*,y*)是局部渐近稳定的,且两种群受密度制约,则E*(x*,y*)是全局稳定的. 图2、图3的生物意义是:在庇护所保护下,虾和贝类等种群经过一定的时间后,种群密度将达到一个平衡点,也就是稳定状态.那么在条件不改变的情况下,虾和贝类等种群的密度在整个环境中将一直在这一点保持稳定. 模型(4)所取数值如下: m=1.2,q=0.3,α=10,k=100,β=0.6,a=0.02,b=0.01,c=0.02,n=0.01,γ=0.09. 图4、图5表明:当模型(4)有正解,且解有界时,若模型不稳定,该模型存在一个极限环. 图4、图5的生物意义是:在庇护所保护下,虾和贝类等种群密度在经过使种群保持平衡的点时,平衡点的稳定性丧失.虾和贝类等种群密度的大小趋于有规律的周期性震荡而不再稳定.在休整期时间内,人们不能再对海洋里的虾和贝类等进行捕捞;虾和贝类等物种不断繁衍,使种群数量持续增加.休整期过后,虾和贝类等物种的密度仍然在增加,而人们的捕捞量也随之增加.逐渐地,虾和贝类等物种的密度减少,同时,人们的捕捞量也减少.人们的捕捞量与虾和贝类等物种的密度同时上升或下降,周而复始而产生的极限环使虾和贝类等物种的种群生态稳定、长期共存,从而使虾和贝类等物种的种群与人们的捕捞量协同进化. 图4 模型(4)的不稳定性 图5 模型(4)的极限环 研究食饵在庇护所保护下,对具有种间、种内干扰的和Holing-Ⅱ型功能反应函数影响的食饵-捕食者模型.并且考虑了食饵在庇护所保护下的死亡率,运用了雅克比行列式等方法,不断对食饵-捕食者模型Holing-Ⅱ功能反应函数及庇护所的效应进行修正.合理地使动力系统的方法与微分方程相结合,对食饵在庇护所保护下受 Holing-Ⅱ功能反应函数影响的食饵-捕食者模型的动力行为进行了分析,得到平衡点有000正解且一致有界,还得到了能够判断模型全局稳定和不稳定的条件.此外,当模型不稳定时,得到了模型存在极限环. 在未来的工作中,对食饵在庇护所保护下受Holing-Ⅱ功能反应函数影响的食饵-捕食者模型,应考虑环境污染、时滞现象等对其动力行为的影响,使模型与实际更紧密联系,可行性更强. [1] 王克.随机生物数学模型[M].北京:科学出版社,2010:124-130. [2] 陈江彬.具避难所的捕食者-食饵系统的定性研究[J].福州大学学报(自然科学版),2014,42(6):812-818. [3] KAR T K.Stability Analysis of a Prey-predator Model Incorporating a Prey Refuge[J].Communications in Nonlinear Science and Numerical Simulation,2005,10(6):681-691. [4] CHEN F D,CHEN L J,XIE X D.On a Leslie-gower Prsedator-prey Model Incorporating a Prey Refuge[J].Nonlinear Asnalysis:Real World Applications,2009,10(5):2905-2908. [5] 张子振,汪凯.食饵具有庇护的时滞捕食系统稳定性和Hopf分支[J].浙江大学学报(理学版),2014,41(6):642-649. [6] HASSELL M P.Mutual Interference between Searching Insect Parasites[J].The Journal of Animal Ecology,1971,40(2):473-486. [7] LV Y S,DU Z J.Existence and Global Attractivity of a Positive Periodic Solution to a Lotka-volterra Model with Mutual Interference and Holling III Type Functional Response[J].Nonlinear Analysis:Real World Applications,2011,12(6):3654-3664. [8] 王顺庆,王万雄,徐海根.数学生态学稳定性理论与方法[M].北京:科学出版社,2004:115-126. [9] CHEN L J,CHEN F D.Global Analysis of a Harvested Predator-prey Model Incorporating a Constant Prey Refuge[J].International Journal of Biomathematics,2010,3(2):205-223. [10] 农业部渔业局.2011中国渔业统计年鉴[M].北京:中国农业出版社,2011:61-73.2 基本结果

2.1 系统的稳定性







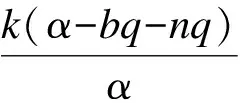
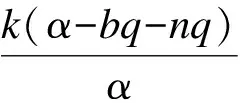
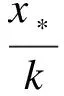

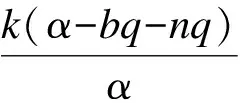










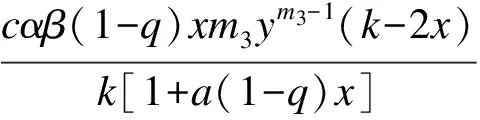
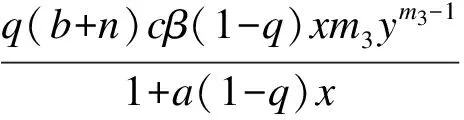
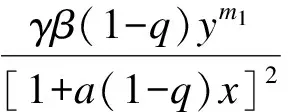




2.2 极限环的存在性


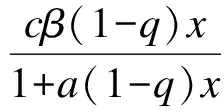








3 应用实例与数值模拟




4 结 论
