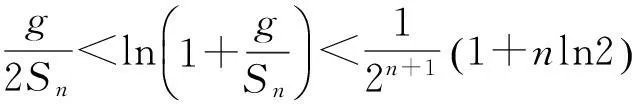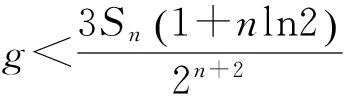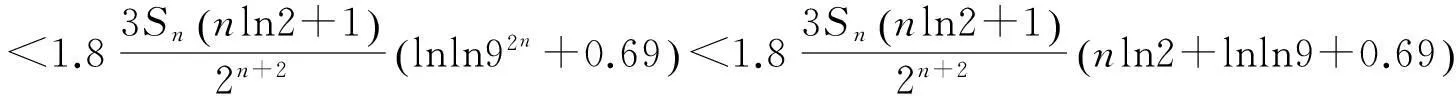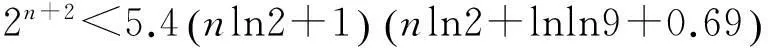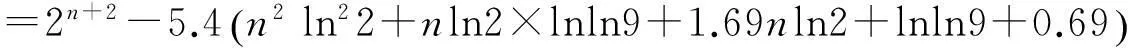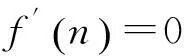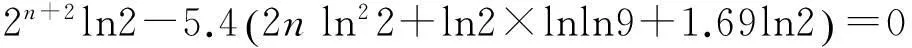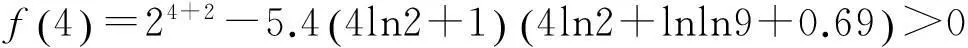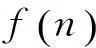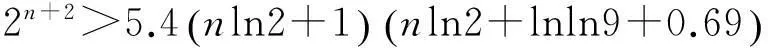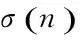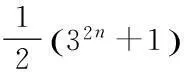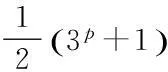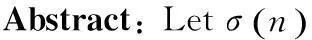一类正整数是否为孤立数研究

孙树东

(新疆警察学院信息安全工程系， 乌鲁木齐830011)

摘要：设是正整数n的所有正约数之和。如果正整数n，m满足=m+n，则(m,n)被称为一对相亲数。相反地，对于给定的正整数n，若不存在任何正整数m满足=m+n，则称n为一个孤立数。讨论了正整数是否为孤立数的问题，证明了其是孤立数的结论，其中n是任意的正整数。

关键词：相亲数；完全数；孤立数

收稿日期:2015-01-24

作者简介:孙树东(1958-)男,辽宁彰武人,讲师,主要从事高等数学理论应用与教学研究。

中图分类号：O156文献标志码：A

0引言

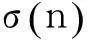
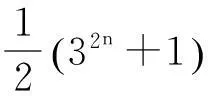
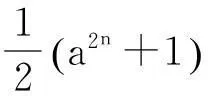
1引理

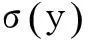
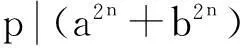
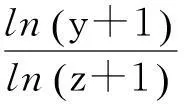
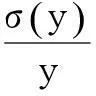
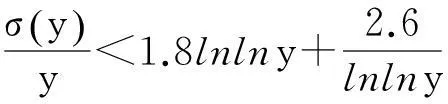
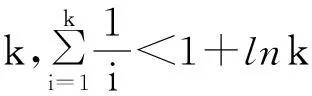
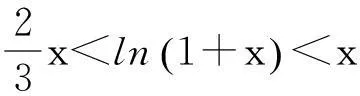
2定理及其证明

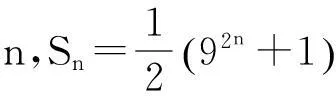
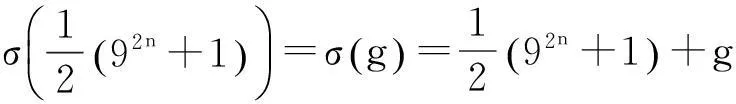
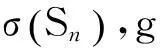
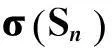
表1　S n的标准分解式、对应的 、g和 的值

由表1可知，n=1，2，3时，Sn都是孤立数。因此，只考虑n≥4的情况。由引理1，可得

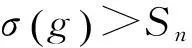
即g>224。

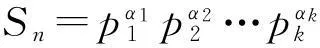
故有

pi-1≥2n+1i，i=1,2,…,k。

(1)

于是，由(1)式可得，

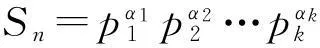
(2)

又因为n≥4，则由(2)式及引理3，有

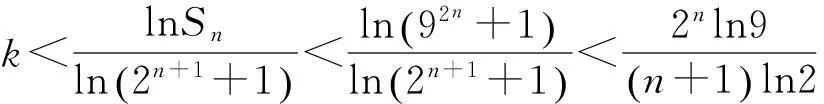
(3)

由引理4有

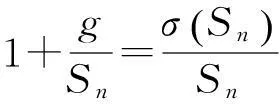
(4)

于是由(4)式和引理7，(1)式及引理6两边取对数可得，

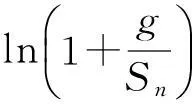
(5)

由(3)式和(5)式可得，

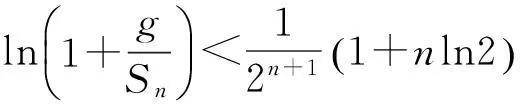
(6)

假设g≥Sn，则由(6)式有，

ln2，

即

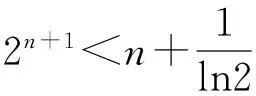
(7)

由于n≥4可知，则(2-7)式不可能成立。于是，g

则有

(8)

因为g>224，所以lnlng>2.8。于是，由(2-3)、(2-8)式和引理5可得，

即

(9)

设

(10)

由(10)式可得，

则

则

故当n≥4时，(9)式是不可能成立的。因此，当n≥4时，Sn都是孤立数，于是定理得证。

参考文献:

[1]GuyRK.Unsolvedproblemsinnumbertheory[M].NewYork:SpringVerlag, 1981.

[2]YanSY. 2500yearsinthesearchforamicablenumbers[J]. 数学进展，2004,33(4):385-400.

[3]乐茂华. 2的方幂是孤立数[J]. 四川理工学院学报，2005，18(3)：1-4.

[4]乐茂华. 奇素数的平方都是孤立数[J]. 周口师范学院学报，2006，23(5)：4.

[5]乐茂华. 形如p2r的孤立数[J]. 商丘师范学院学报，2006，22(5)：25-26.

[6]LucaF.Theanti-socialFermatnumbers[J].AmerMathMonthly, 2000, 107:171-173.

[10]沈忠华. 关于亲和数和完全数的一个注记[J]. 黑龙江大学学报，2006，23(2)：250-251.

[12]AlbertHBeiler.Recreationsinthetheoryofnumbers(Chineseedition)[M].Shanghai:ShanghaiEducationalPublishingHouse(SEPH),1998, 211.

[13]ROSSERJB,SCHOENFELDL.Approximateformulasforsomefunctionsofprimenumber[J].IllinoisofMath, 1962, (6):64-96.

[14]李伟勋．Mersenne数Mp都是孤立数[J]．数学研究与评论，2007，27(4))：693-696．

责任编辑：程艳艳

Study on Whether a Class of Positive Integers are Anti-sociable Numbers

SUN Shudong

(Department of Information Security Engineering， Xinjiang Police Academy, Urumqi 830011, China)

Keywords：amicable numbers; perfect number; anti-sociable number