齿轮参数激光周扫系统检测精度分析

齿轮参数激光周扫系统检测精度分析

孙峰1,2，苏成志1

(1.长春理工大学机电工程学院，长春130022；2.长春汽车工业高等专科学校，长春130013)

摘要：针对齿轮参数激光周扫检测系统精度分析问题，应用拓扑分析方法与多体运动学理论建立了齿轮测量数学模型，把误差分析问题转化为坐标系变换问题，解决了通过传统的误差传递方法难以探究高复杂度系统检测精度的难题；通过数值仿真分别分析了12个单项误差源对该系统检测精度的影响，综合误差计算表明：基于目前的转台制造精度和激光检测水平，该系统检测精度可达0.003mm。

关键词：激光周扫；检测精度；多体拓扑；误差转换

收稿日期:2014-05-28

基金项目:国家自然基金(50775014);吉林省科技支撑计划项目(20110313)。

作者简介:孙峰(1982-)，男，朝鲜族，黑龙江佳木斯人,硕士研究生，主要从事在线检测理论与技术方面的研究；苏成志(1977-)，男，副教授，博士，主要从事机电系统、光电检测方面的研究。

中图分类号：TN249文献标志码：A

0前言

目前的齿轮测量方法[1-2]基本上可以分为四种方法：机械几何解析测量法、齿轮啮合滚动式综合测量法、CNC坐标测量法和非接触式齿轮测量法。上述方法从测量原理上来讲属于相对测量，易于实现齿形、齿向和周节等齿轮误差的测量，但对端跳、齿根圆圆度、齿根圆圆柱度和全齿高等齿轮参数的测量却是技术难题。这些参数的测量是齿轮工艺参数改进与优化的依据，是目前齿轮测量中亟需解决的问题。本文提出了齿轮参数激光周扫方法。由于齿轮参数激光周扫检测系统的复杂性，难以通过传统的误差传递方法探究该系统的检测精度。为此，应用拓扑分析方法与多体运动学理论[3-4]建立其数学模型[5]，把误差分析问题转化为坐标系变换问题，并结合数值计算进行精度仿真分析，为该系统的研制奠定了考量基础。

1齿轮参数激光周扫检测原理

如图1所示，齿轮参数激光周扫检测系统由大理石基座、气浮旋转台、激光位移传感器、升降丝杠、升降丝杠电机、滑台、支撑立柱七部分组成。测量步骤为，被测件8放于大理石基座1上静止不动, 由升降丝杠4及驱动电机5完成测头Z轴方向的升降，实现不同截面扫描；气浮旋转台6完成同一截面的周扫运动；滑台3完成同一截面内测量半径的变化；在滑台3位置确定的前提下，由激光位移传感器2对被测件进行测量；支撑立柱7用于支撑测量结构的整体重量。扫描齿轮结束后，利用扫描的数据重构齿轮，并与数字齿轮比较获得齿轮误差[6]。

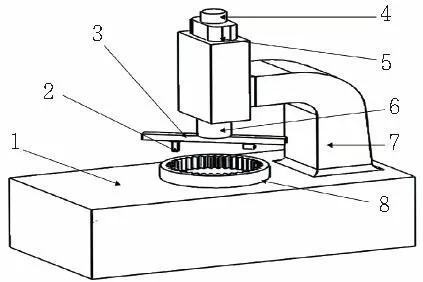
图1　齿轮参数激光周扫检测系统 1.大理石基座　2.激光位移传感器　3.滑台　4.升降丝杠　5.升降丝杠电机　6.气浮旋转台　7.支撑立柱　8.被测件

2建立数学模型模

2.1　齿轮参数激光扫描检测系统结构拓扑

应用多体拓扑学中的连续映射分析法[7]，对图1所示的模型建立齿轮参数激光扫描检测系统的进行结构拓扑[8]，如图2所示，B, G, T1,T2,T依次为低序到高序体，本拓扑结构具有两个分支。

2.1.1　激光位移传感器和基座分支

设大理石基座为第1体B，O1为该体参考点；支撑立柱为第2体T1，O2为该体参考点；气浮旋转台为第3体T2，O3为该体参考点；激光位移传感器为第4体T，O4为该体参考点。

2.1.2　齿轮和基座分支

设大理石基座为第1体B，O1为该体参考点；被测件为第2体G,O5为该体参考点。

矢量q1代表体T1参考点O2相对于体B参考点O1的位置矢量；矢量q1e代表体T1参考点O2相对于体B参考点O1的位置误差矢量；矢量S1代表体T1参考点O2相对于体B参考点O1的位移矢量；矢量S1e代表体T1参考点O2相对于体B参考点O1的位移误差矢量。

矢量q2代表体T2参考点O3相对于体T1参考点O2的位置矢量；矢量q2e代表体T2参考点O3相对于体T1参考点O2的位置误差矢量；矢量S2代表体T2参考点O3相对于体T1参考点O2的位移矢量；矢量S1e代表体T2参考点O3相对于体T1参考点O2的位移误差矢量。

矢量rw，rg分别为测量点相对于体T坐标系参考点O4和体G坐标系参考点O5的位置矢量。

2.2　几何运动数学模型

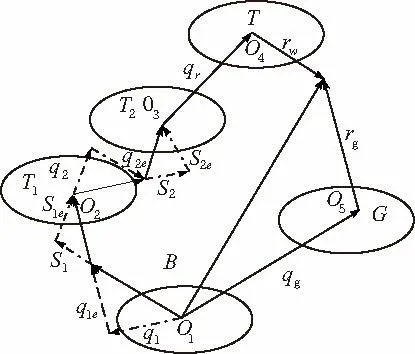
图2　拓扑结构图

由图2建立各体的坐标系[9-10]。以第1体B的参考点O1为原点，建立坐标系{A}，以此类推，以各体的参考点为坐标原点建立坐标系{B}、{C}、{D＇}和{D}。

根据多体系统运动学理论，建立的几何运动数学模型[11]如下：

(1)

(2)

(3)

因为矢量rw，rg分别为测量点相对于坐标系{D＇}原点和坐标系{D}原点的位置矢量，故设

(4)

(5)

将式(4)、 (5)代入式(3)，整理得到齿轮参数激光周扫检测的测量方程如下：

至此，实现了把误差分析问题转化为了坐标系变换问题。

(6)

式中：

s表示sin，c表示cos，本文将一律采用此约定；

z为测头所在截面高度坐标；δ为被测件半径方向向量与Y轴逆时的针夹角；L1是气浮旋转台旋转中心到其在测量平台投影中心的距离，即理想旋转轴高度； θ1=θ2=θ3=arcsin(v/L1),x轴相对转角为θ1，y轴相对转角为θ2，z轴相对转角为θ3,旋转轴v为不垂直度引起水平位移，即旋转轴机械加工径向跳动；θ4=θ5=θ6=arctan(L轴/R1), x轴相对转角为θ4，y轴相对转角为θ5，z轴相对转角为θ6,设气浮旋转台轴向跳动为L轴,选用气浮旋转台的半径为R1; L径(Lx、Ly、Lz)为气浮旋转台径向跳动； Ljx、Ljy、Ljz为由激光测长误差分解为出的x、y、z轴上的分量误差；式(6)为齿轮参数激光周扫检测系统的几何运动数学模型。在不考虑本系统变形及间隙问题时，可知本系统包括12项运动参数,如表1所示。

表1　12项运动参数表

3误差分析

为了分析本系统精度情况，下面通过测量模型(6)，并结合数值计算进行精度仿真，图3为齿轮测量仿真齿形模拟图。

1)设被测量齿轮直径范围为50mm~300mm，高度为100mm，被测件给定齿轮齿数为88，被测件给定齿轮模数为3.4，如图3(a)为仿真给定的标准数字齿轮。

2)设齿轮参数激光周扫检测系统结构尺寸如下：气浮旋转台旋转中心到其在测量平台投影中心的距离L1=110mm，气浮旋转台旋转半径R1=200mm。

3)设齿轮参数激光周扫检测系统数据采样率为：12600000点/周。

4)设齿轮测量的初始位置:测件给定齿轮形心x坐标x0=0mm;测件给定齿轮形心y坐标y0=0mm，测件给定齿轮形心z坐标z0=0mm。

图3(b)为齿轮参数激光周扫系统检测系统的气浮旋转台旋转轴线相对于大理石基座不垂直时，齿形仿真结果图；图3(c)为气浮旋转台晃动测量时，齿形仿真结果图；图3(d)为激光位移传感器有测量误差时，齿形仿真结果图；图3(e)为气浮旋转台旋转角度有误差时，齿形仿真结果图。

3.1　单项误差分析

由表1可知，12项运动参数可分为4项误差源，下面对4项误差源分别进行分析：

3.1．1　不垂直度误差与测量半径误差关系

由齿形仿真图3(b)可知，由于齿轮参数激光周扫系统检测系统的气浮旋转台旋转轴线相对于大理石基座不垂直，造成齿形测量截面整体呈椭圆形。

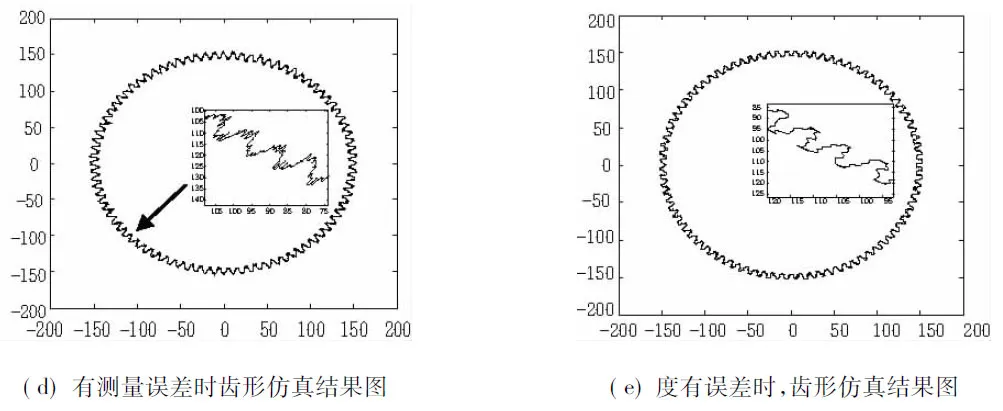
图3　齿轮测量仿真齿形模拟图

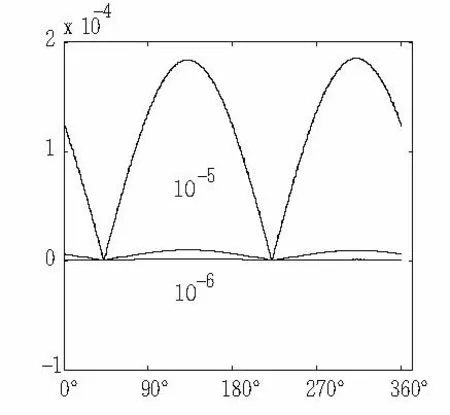
图4　不垂直度与测量半径误差关系曲线图

设被测件测量起始位置方向向量与Y轴成逆时针45°夹角，测量系统的不垂直度V分别为0.01mm、0.1mm、1mm，代入式(6)，不计其它误差，周扫(360°)后的齿轮半径仿真误差如图4。

由图4可知，齿轮参数激光周扫系统检测系统的气浮旋转台旋转轴线相对于大理石基座不垂直度误差对测量半径误差影响很小,当旋转轴系不垂直度水平位移(径向跳动)为10mm时，测量半径误差最大为0.00018mm数量级。机械加工旋转轴系只要保证不垂直度V≤0.01mm即可，此时测量半径误差为10-6mm数量级。

3.1.2　气浮旋转台晃动误差与测量半径误差关系

由齿形仿真图3(c)可知，气浮旋转台晃动对齿形径向和轴向测量精度均产生影响。

1)设气浮旋转台径向晃动与轴向晃动为L径=L轴≤0.00001mm(正态随机分布随机数模拟气浮旋转台晃动量，幅值最大值为0.00001mm)，代入式(6)，不计其它误差，测量一周(360°)仿真结果如图5；

2)设气浮旋转台径向晃动与轴向晃动为L径=L轴≤0.0001mm(正态随机分布随机数模拟气浮旋转台晃动量，幅值最大值为0.0001mm)，代入式(6)，不计其它误差，测量一周(360°)仿真结果如图6；

由图5与图6对比可知，气浮旋转台晃动误差即径向跳动与轴向跳动是由所选购气浮转台自身决定的，若高精度的气浮旋转台径向跳动与轴向跳动基本为≤0.0001mm，由仿真结果得，引起测量半径最大误差为0.00042mm，平均误差影响为0.00015mm;若高精度的气浮转台径向跳动与轴向跳动均为≤0.00001mm，引起测量半径最大误差为0.000034mm，平均误差影响为0.000016mm；气浮旋转台径向跳动与轴向跳动精度的提高对半径测量误差影响不大，仅提高一个数量级，但制造成本增加很大。所以气浮旋转台径向跳动与轴向跳动均为≤0.0001mm时，引起测量半径最大误差为0.00042mm，平均误差影响为0.00015mm，可以满足半径测量误差0.003mm要求。

图5　转台晃动误差与测量半径误差关系曲线图

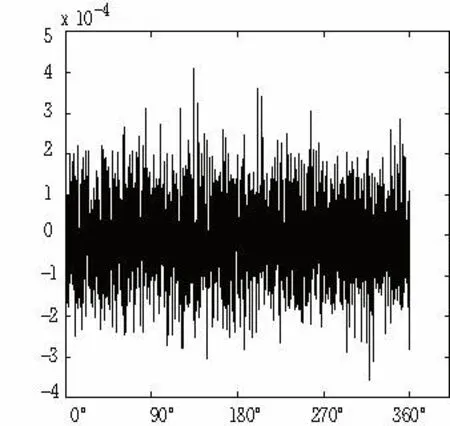
图6　转台晃动误差与测量半径误差关系曲线图

3.1.3　激光位移传感器测量与测量半径误差关系

由齿形仿真图3(d)可知，激光位移传感器测量误差对齿形径向测量精度产生影响。

1)设激光位移传感器测量位移误差为Lj(Ljx、Ljy、Ljz)≤0.0001mm(正态随机分布随机数模拟激光位移传感器测量位移误差量，幅值最大值为0.0001mm)，代入式(6)，不计其它误差，测量一周(360°)仿真结果如图7；

2)设激光位移传感器测量位移误差为Lj(Ljx、Ljy、Ljz)≤0.0001mm(正态随机分布随机数模拟激光位移传感器测量位移误差量，幅值最大值为0.001mm)，代入式(6)，不计其它误差，测量一周(360°)仿真结果如图8。

由图7与图8对比可知，激光器位移传感器位移测量误差是由激光器位移传感器精度自身决定的，当激光位移传感器测量位移误差精度为≤0.0001mm时，引起测量半径最大误差为0.00031mm，平均误差影响为0.000015mm; 当激光位移传感器测量位移误差精度为≤0.001mm时，引起测量半径最大误差为0.0039mm，平均误差影响为0.0015mm。

因此，测量位移误差精度为≤0.0001mm的激光位移传感器，既可以满足测量要求0.003mm。

图7　激光器位移测量误差与测量半径误差关系图

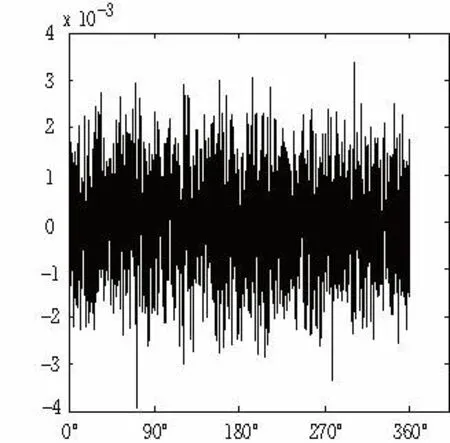
图8　激光器位移测量误差与测量半径误差关系图

3.2　综合误差分析

以上分析了各单项误差对齿轮测量精度的影响，下面分析旋转轴线不垂直度V，气浮转台晃动L径=L轴，激光位移传感器测量位移误差量，气浮旋转台旋转角度误差对齿轮测量精度的综合影响。1)设齿轮参数激光周扫检测系统不垂直度V为0.01mm，气浮转台轴向晃动与径向晃动为L径=L轴≤0.0001mm，激光位移传感器测量位移误差为Lj(Ljx、Ljy、Ljz)≤0.0001mm，代入式(6)，不计其它误差，测量一周(360°)仿真结果如图9所示。2)设齿轮参数激光周扫检测系统不垂直度V为0.01mm，气浮转台轴向晃动与径向晃动为L径=L轴≤0.001mm，激光位移传感器测量位移误差为Lj(Ljx、Ljy、Ljz)≤0.001mm，代入式(6)，不计其它误差，测量一周(360°)仿真结果如图10所示。

对比图9与图10可知：保证齿轮参数激光周扫检测系统的旋转轴系不垂直度V≤0.01mm，气浮旋转台的径向跳动与轴向跳动均为≤0.0001mm，激光位移传感器测量位移误差量为≤0.0001mm的前提下，综合误差引起的测量半径最大误差为0.00042mm，平均误差影响为0.00015mm。

目前机械设计制造方法可以达到并保证齿轮参数激光周扫检测系统的旋转轴系不垂直度V≤0.01mm，气浮旋转台的径向跳动与轴向跳动均为≤0.0001mm，激光位移传感器测量位移误差量为≤0.0001mm，且综合仿真测量结果为0.00015mm，故本系统设计的测量精度为0.001mm。

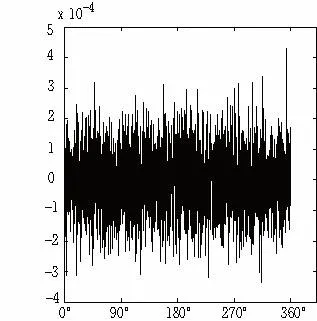
图9　综合误差与测量半径误差关系图

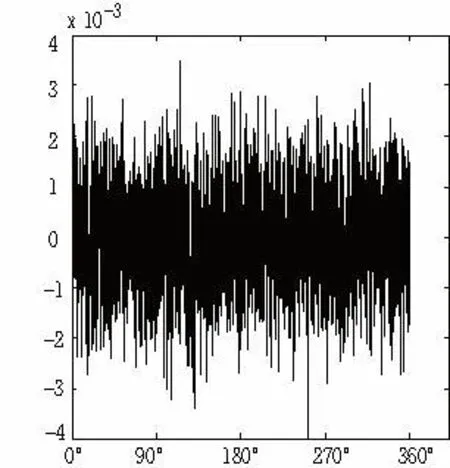
图10　综合误差与测量半径误差关系图

4 结语

应用拓扑分析方法与多体运动学理论建立了齿轮测量数学模型，通过数值仿真分别分析了12个单项误差源对该系统检测精度的影响，仿真结果表明：

1)建立了几何运动数学模型，把误差分析问题转化为坐标系变换问题，解决了通过传统的误差传递方法难以探究高复杂齿轮参数激光周扫检测系统的精度分析问题；

2)根据当前的气浮旋转台制造精度和激光位移检测水平，齿轮参数激光周扫检测系统的精度可达到0.003mm。

参考文献:

[1]石照耀. 齿轮测量技术100年—回顾与发展[J].中国工程科学， 2003,5(9):17-18.

[2]魏华亮.我国CNC齿轮测量中心的发展现状[J]．计量技术.2004，l(9):24-28．

[3]R.L休斯顿，刘又午.多体系统动力学(上、下册)[M].天津：天津大学出版社，1987.

[4]FANJW,GUANJL,WANGWC,etal.AuniversalmodelingmethodforenhancementthevolumentricaccuracyforCNCmachinetools[J].JournalofMaterialsProcessingTechnology,2002，129(6):624-629.

[5]陈凯云，叶佩青，俞学云，等.BLM001型叶片测量仪准刚体数学建模研究[J].航空精密制造技术，2004,5(6):23-26.

[6]刘晶.重构模型精度的评价和产品改进[J].机床与液压，2010，38(21):5-6.

[7]李艳颖.拓扑空间及其连续映射的概念[J].教育教学研究，2010(2)：117-119.

[8]范晋伟，刘宏旭，胡勇，等.3920型齿轮测量中心几何结构建模分析[J].中国工程机械学报. 2006,4(2):36-39.

[9]江兵，倪刚，吴迪.基于坐标系统拓展的改进定位算法[J].计算机工程，2008，34(20)：7-8.

[10]范晋伟，刘宏旭，胡勇，等.基于多体运动学理论的齿轮测量中心几何结构建模分析[J].制造技术与机床，2007，3(2)：80-82.

[11]蔡自兴.机器人学[M].北京：清华大学出版社,2009.

责任编辑：吴旭云

Analysis of Detection Precision of Gear Parameter Laser Circling Scan System

SUN Feng1，2，SU Chengzhi1

(1. School of Mechatronical Engineering, Changchun University of Science and Technology, Changchun 130013, China; 2.Changchun Automobile Industry Institute, Changchun 130013, China)

Abstract：In view of the detection precision of gear parameter laser circling scan system, a mathematical model of the gear measurement is constructed by using topology analysis method and multi-body kinetics theory. Then the error analysis problem is transformed into the problem of coordinate system transformation, and the problem of the system detection accuracy with high complexity is solved, which is difficult to be explored by the traditional error transfer methods. In addition, the effect of 12 single error sources on the detection precision of the system is analyzed through numerical simulation. The calculation result of comprehensive error shows that the detection accuracy of the system can reach 0.003mm based on the current turntable manufacturing precision and laser detection level.

Keywords：laser circling scan; detection accuracy; multi-body topology; error conversion