H-矩阵预条件Gauss-Seidel迭代法及其收敛性

H-矩阵预条件Gauss-Seidel迭代法及其收敛性

薛炜

(甘肃建筑职业技术学院基础部,兰州730050)

摘要：提出了预条件矩阵I+Cα, 并利用此矩阵讨论了H-矩阵方程组的预条件Gauss-Seidel迭代法的收敛性. 一些谱半径的比较结果也被给出。

关键词：H-阵; Gauss-Seidel迭代法; 预条件; 收敛性

收稿日期:2015-03-05

基金项目:甘肃省建筑科技教育规划项目(20153675)

作者简介:薛炜，(1981-)，男，甘肃静宁人，讲师，硕士，主要从事数学教育，应用数学方面研究。

中图分类号：O241.6文献标志码：A

0引言

考虑线性方程组

Ax=b,

(1)

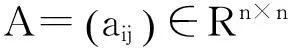
对于A的任意分裂A=M-N，其中M是非奇异矩阵，用迭代法求解(1)的基本迭代格式是

(2)

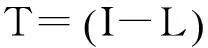
为了更好地解线性方程组(1), 引入非奇异预条件矩阵MP, 即考虑解方程组

PAx=Pb,

(3)

或者解方程组

(4)

与

P-1x=y，

在一般情况下选取的预条件矩阵P都是易于求逆的, 故只解(3)与(4)。

令PA=MP-NP, MP是非奇异矩阵, 则解(3)的Gauss-Seidel迭代法的迭代格式是

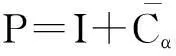
本文利用文献[2]的方法, 给出了线性方程组改进的Gauss-Seidel迭代法对于H-矩阵的收敛性定理。

在本文中, 我们用右乘预条件矩阵的方法，讨论了预条件迭代法的收敛性。我们取预条件矩阵为：

记

则

显然

I-L+Cα-LCα

与

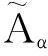
2预备知识

定义称为Z-矩阵, 若aij0, i≠j,i,j=1,2,…,n。

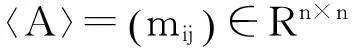
i≠j,i,j=1,2,…,n。

定义4 [3]矩阵分裂A=M-N称为

(1)M-分裂, 如果M是M-矩阵, 且N≥0;

(2) 弱正则分裂, 如果M-1存在且M-1≥0, M-1N≥0;

(3) 正则分裂, 如果M-1存在且M-1≥0, N≥0。

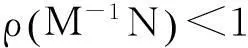
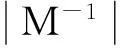
引理3 [4]若A≥0且为不可约n×n矩阵, 则有

引理4 [3]设A≥0, 则

引理5 [5]A是H-矩阵的充分必要条件是存在向量x>0, 使得x〈A〉>0。

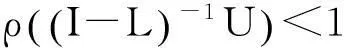
引理7 [6]如果A是H-矩阵, 且ai1≠0(i=2,3,…n), 若设

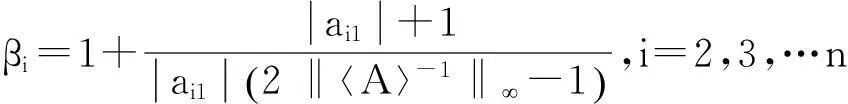
则βi>1。

引理8 [7]设A是Z-矩阵, 则下列条件等价：

(1)A是非奇异M-矩阵;

(2)A的所有主子矩阵是非奇异M-矩阵;

(3) 所有的主子式是正的。

3主要结论

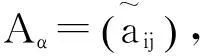
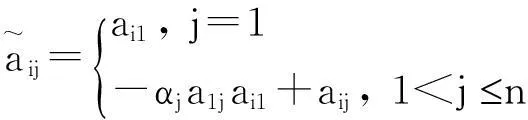
令x=e〈A〉-1, 因为A是H-矩阵, 所以〈A〉是M-矩阵. 从而〈A〉-1≥0, 故x≥0。

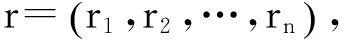
即有

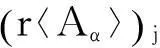
(5)

当j=1时,

(6)

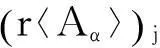
(2) 如果αj>1, 那么由(5)式知, 对任意的2jn, 有

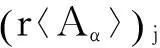
从定理的证明过程可知, 如果不满足条件a1j≠0, (j=2,3,…,n)时, 则对任意的

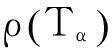
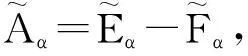
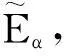
当i=1时, e11=1. 因为〈A〉是非奇异M-阵,根据引理8, 有

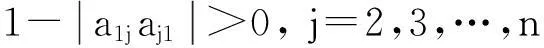
又αj∈[0,1], 则

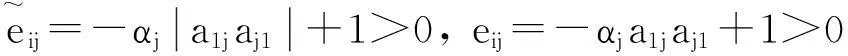
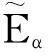
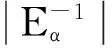
当i>j≥2时,

当i>j=1时,

则

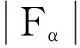
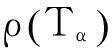
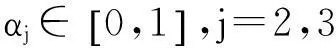
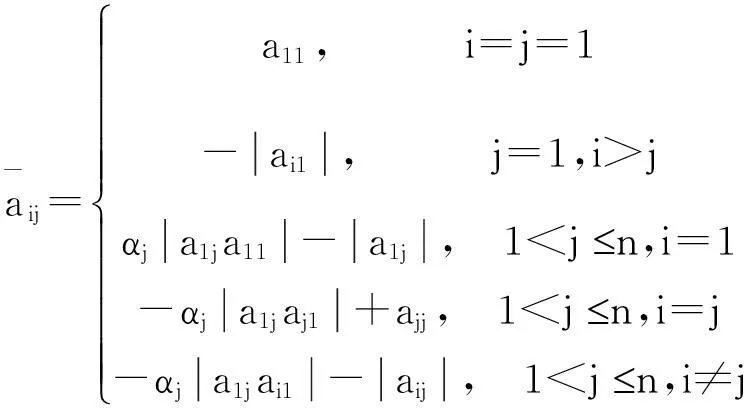
而

又

记

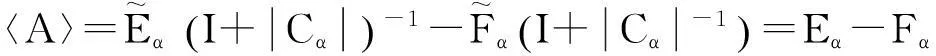
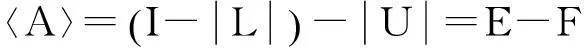
由

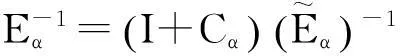
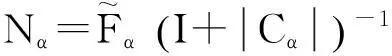
则

〈A〉=Eα-Fα

是〈A〉的弱正则分裂, 又M-阵的Gauss-Seidel分裂是弱正则分裂且收敛, 所以

〈A〉=E-F

也是〈A〉的弱正则分裂。这样

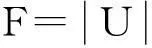
由引理2, 有

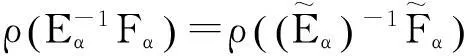
参考文献:

[1]程光辉，等. 解线性方程组的预条件Gauss-Seidel型迭代法[J]. 应用数学与力学, 2006(09)：1117-1121.

[2]孙丽英. IMGS方法对于H-矩阵的若干令人满意的改进[J]. 数学物理学报, 2006, 26A(4)：591-594.

[3]宋永忠. 线性方程组的迭代解法(讲义)[M]. 南京: 南京师范大学出版社, 1992.

[4]张保祥.H-矩阵的预条件AOR迭代法及其收敛性[J]. 齐齐哈尔大学学报, 2008(06):69-71.

[5]胡家赣. 线性方程组的迭代解法[M]. 北京: 科学出版社, 1999.

[6]柳卫东, 畅大为.H-矩阵的预条件Gauss-Seidel迭代法[J]. 西南民族大学学报, 2007(05):1009-1012.

责任编辑：程艳艳

Preconditioned Gauss-Seidel Iterative Method for H-matrix and the Convergence

XUE Wei

(Department of Basic Courses, Gansu Construction Vocational Technical College, Lanzhou 730050, China)

Abstract：This paper presents a preconditioned matrix I+Cα, discusses the convergence of the preconditioned Gauss-Seidel iterative method for H-matrix equations and gives some comparative results of spectral radius.

Keywords：H-matrix; Gauss-Seidel iterative method; precondition; convergence