一种查表与插值法在微控制器中的实现

史永胜， 胡　双， 许梦芸， 王喜锋

(陕西科技大学 电气与信息工程学院， 陕西 西安　710021)



一种查表与插值法在微控制器中的实现

史永胜， 胡双， 许梦芸， 王喜锋

(陕西科技大学 电气与信息工程学院， 陕西 西安710021)

摘要：在微控制器中断程序中，大量的长时间计算是不可取的.为了提高计算效率，提出了一种在软件上将调用编译器中函数库求解复杂函数的方法，改为查表与插值的方法.这种查表插值方法的引入，在理论上能提高编译器在该段程序的编译效率和程序在微控制器中的执行速度，具有高效性.本文以STM32F407VGT6微控制器为硬件平台，设计了控制变量法的对比实验.结果表明，该方法能有效减少程序运行时间，适用于大多复杂函数，并且适用于不同主频的微控制器，从而验证了该方法的通用性与高效性.

关键词：查表； 插值; 微控制器； 计算速度； 计算精度

0引言

在微处理器程序运行的过程中，特殊情况下需要计算复杂函数在某一点的值[1]，如开方运算、三角函数与反三角函数运算、指数与对数运算等.如果在中断服务程序中执行类似操作，会导致运算时间太长.这是因为完成这些工作的计算一般都是通过调用编译器的math.h文件中的函数库来完成的，而这种方法编译效率偏低[2].math.h头文件是针对所有处理器的，其运算函数都是基于定点CPU和标准算法(IEEE-754)[3]，并没有预见使用FPU(浮点运算单元)的情况，因而需要很多指令和复杂的过程才能完成运算，这就增加了运算时间，这是开发者和用户所不希望看到的.

在这种情况下，抛弃编译器的函数库，转向通用的查表与插值[4]方法就应运而生.查表与插值的方法在插入的节点足够多的情况下，只要求硬件内存足够大，通过软件的方式[5]计算即可.其可行性高，若微控制器一旦使用了这种方法，定时精度将有效提高，故在测频、信号的采样与恢复、逆变器、电机控制和无线充电技术等方面的应用将更加高效.其高效性是调用math.h的方式所无法企及的.

本文采用控制变量法，以微控制器STM32F407VGT6[6]为硬件平台，通过设计实验比较了两种方式下程序的运行时间,得出了将查表与插值算法引入微控制器中，可带来立竿见影的提升效果的结论.

1查表与插值在微控制器中的实现

1.1查表与插值法介绍

查表是通过调用位于内存中的二维或多维数组中的值来实现的方法，具有计算量小的特点.插值法是函数逼近的一种重要方法，是数值计算的基本课题.对于具有唯一插值函数的多项式插值和分段多项式插值，对其中的多项式插值主要讨论n次多项式插值的方法，即给定n+1各点处的函数值后，怎样构造一个n次插值多项式的方法.现已成熟的插值法包括lagrange插值、newton插值、hermite插值、分段多项式插值及样条插值[7]等方法.

本文所使用的插值法方法类似于三次样条插值，采用查表与插值结合的方式.在工程上使用三次插值函数一般能满足足够的计算精度.该方法可应用于实现一些数字量到模拟量的输出.输出数字量频率越高，经过采样还原后输出的模拟量的谐波含量越低.如在进行逆变器SPWM输出时，需要在微控制器中提高开关频率，即提高定时器的定时频率，但中断服务函数内进行正弦计算时占用CPU时间较长.这里采用三次插值后，能有效减少计算所用时间，提高定时频率.在节点足够多的情况下，最终模拟量输出精度不仅不会降低，反而会提高.

1.2查询表的生成

对于函数f(x),依据精度将该函数的定义域在特定区间内等分为N份，即构成N+1个节点，用Matlab、VisualC++或其它工具求出每个节点的函数值，输出数据表，并将数据表以浮点型常量形式放入到微控制器内存中.

在该方法中，求任何点的函数值都需要四个节点，因此需在函数表内需要给出至少N+3个点的值，故要加入定义域外的一些节点，如节点N-1、N+1、N+2，加上定义域内的N个节点，共N+3个节点，这样才能覆盖整个定义域内的所有值.

此方法需要较大的内存空间，对微控制器有一定要求.针对特殊应用可以实现若干个函数，不需要囊括所有函数.比如，在逆变器、变频器等应用编程中，只需用此方法求出正弦函数的值；对于可穿戴设备中的加速度传感器(角度传感器)的倾角求值，亦可以用此方法求出反正弦或反正切的值[8].

1.3插值求解的流程

在系统初始化后，先生成出需要调用的函数的N+3个节点的表格；函数原型中，将输入参数的值映射到[0，1]内; 根据输入参数和表格长度，找出自变量的大致位置，取整为index，通过查表找出距离index最近的四个节点，分别为index-1、index、index+1和index+2，它们对应的函数值分别为：

a=Table[index-1]

b=Table[index+0]

c=Table[index+1]

d=Table[index+2]

再通过作差，求实际输入自变量的小数部分fract，根据如下所述式(1)、(2)、(3)、(4)计算三次插值的系数wa,wb,wc,wd;最后根据以上各式和式(1～5)，输出返回函数值a*wa+b*wb+c*wc+d*wd.

(1)

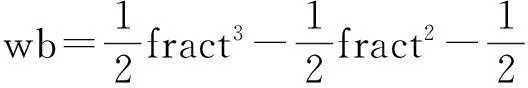
(2)

(3)

(4)

value=a*wa+b*wb+c*wc+d*wd

(5)

软件的具体流程如图1所示.

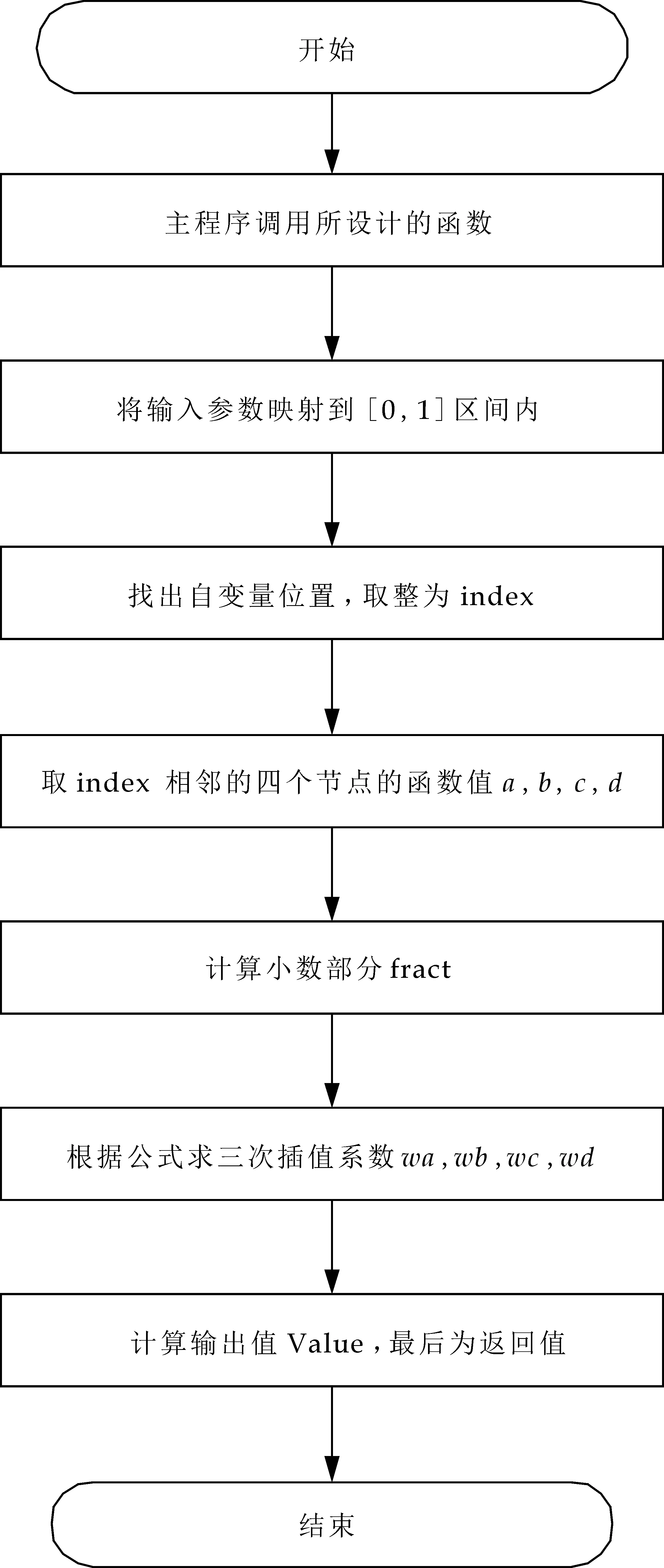
图1　系统软件流程图

程序如下：

float arm_sin_f32(float x)

{

float fract, in;

unsigned int index, tableSize;

float wa, wb, wc, wd;

float a, b, c, d;

int n;

tableSize=(unsigned int)TABLE_SIZE;

in=x*0.159154943;

n=(int)in;

in=in-(float) n;

index=(unsigned int)(tableSize*in);

fract=((float) tableSize*in)-(float)index;

a=sinTable[index-1];

b=sinTable[index];

c=sinTable[index+1];

d=sinTable[index+2];

wa=-0.166666667*fract*fract*fract-

0.333333333* fract+0.5*fract*fract;wb= 0.5*fract*fract*fract-

fract*fract+0.5* fract+1.0;

wc=-0.5*fract*fract*fract+

0.5*fract*fract+fract;

wd=0.166666667*fract*fract*fract-

0.166666667*fract;

return (a*wa+b*wb+c*wc+d*wd);

}

2应用实例

2.1验证平台选择

在逆变器或变频器中产生SPWM所采用的自然采样法，通常是使用正弦波调制三角波的形式，需要实时计算正弦值，这时采用查表与插值的方法就能大大减少程序运行时间.CPU能在很短的周期内处理大量的数据采集、信号分析与输出控制任务，这不仅给软件调试带来了方便，而且还能大大提升定时精度、提高载波的频率，根据SPWM的原理，其输出的SPWM的效果也更接近标准正弦波[9].

ST(意法半导体)推出了以基于ARM®CortexTM-M4为内核的STM32F4系列高性能微控制器，其采用90纳米的NVM 工艺和ART(自适应实时存储器加速器，Adaptive Real-Time MemoryAcceleratorTM).

ART技术使得程序零等待执行，提升了程序执行的效率，从而将Cortext-M4的性能发挥到了极致，使得STM32F4系列可达到168 MHz.自适应实时加速器能够完全释放Cortex-M4内核的性能[10]；当CPU 工作于所有允许的频率(≤168 MHz)时，在闪存中运行的程序，可以达到相当于零等待周期的性能.

STM32F4系列微控制器集成了单周期DSP指令和FPU(Floating Point Unit，浮点单元)，提升了计算能力，可以进行一些复杂的计算和控制.要说明该方法的可行性和通用性，需要主频较高、内存较大的微控制器，而STM32F4能满足这两个条件.同时，作为嵌入式技术的一大进步，STM系列微控制器结合了低成本、低功耗和更多性能等特点[11].

现以ST公司的32位微控制器STM32F407VGT6为平台，以MDK4.72a和IAR Embedded Workbench 两种不同编译器的软件为开发环境，进行了对比实验[12].

2.2验证流程

2.2.1查表数组的生成

在本实例中，采用在Visual C++下输出正弦函数在一个周期内256个节点的值，将区间[0,2pi]进行255份等分，即N=255，共N+1=256个节点.根据章节1.2中描述与分析，需要N+3个节点的值，所以主程序的循环中应从-1开始，止于257，共258个点的值：

for(n = -1; n < (tableSize + 1); n++)

{

sinTable[n+1]=sin(2*pi*n/tableSize);

}

并将sinTable[]数组定义为32位浮点型常量来提高计算精度.

2.2.2在MDK环境下实验

按照上述流程在MDK4.72a下编写程序.

第一，先将STM32F407VGT6的主频设定到最高值168 MHz，经过实验比较直接调用编译器函数库与查表和插值的方法，采用控制其它条件不变的方式，连续求500 000次1.5 rad对应的正弦值，其实验结果如图2与图3所示.对应的调用函数库所用时间为0.354 s,查表与插值法用时0.327 s.

第二，主频在8 MHz时得到的结果如图4与图5所示.对应的调用函数库所用时间为7.443 s,查表与插值法用时6.88 s.

第三，将主频设定到24 MHz、48 MHz、72 MHz、96 MHz、120 MHz、144 MHz等,将所得到的结果汇总如表1和表2所示.

图2　最高主频168 MHz调用函数库所用时间

图3　最高主频168 MHz下插值所用时间

图4　主频8 MHz下调用函数库所用时间

图5　主频8 MHz下插值所用时间

2.2.3在IAR环境下验证

IAR Embedded Workbench 中包含一个全软件的模拟程序 (Simulator).用户不需要任何硬件支持就可以模拟各种ARM 内核、外部设备甚至中断的软件运行环境.从中可以了解和评估IAR的功能和使用方法.

现在将程序移植到具有更高编译效率的IAR Embedded Workbench中，其结果如图6与图7所示.调用函数库所用时间为0.339 s,查表与插值法用时0.321 s,也能得到明显的运算效率提升的结果，而且效果更佳.

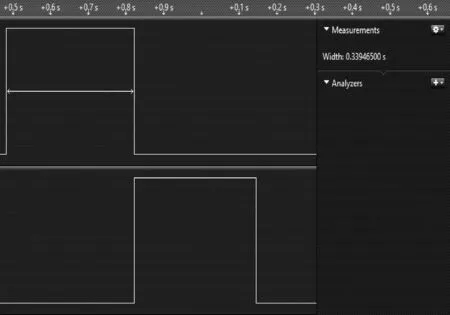
图6　IAR下主频168 MHz时调用函数库所用时间

图7　IAR下主频168 MHz时插值所用时间

使用逻辑分析仪捕捉上述情况微控制器输出的电平，高电平的宽度表示该方法计算500 000次正弦值所用的时间，图2、图4、图6等为调用库函数的方式在LED3管脚输出的波形，而图3、图5、图7等为使用查表和插值的方法在LED4管脚输出的波形.比较图2与图3，图4与图5，图6与图7的高电平时间，可知，无论高频低频或者不同的编译器，插值法较调用编译器函数库更高效[13].

记录各个主频下的效率提升，如表1和表2所示.从8 MHz到168 MHz的不同主频等级，效率提升在7.5%到7.6%之间，由此可知，此方法在不同主频的处理器上也会有有效的效率提升[14].因此,将该方法移植到其它微控制器中，亦具有同样的效果，故具有通用性.

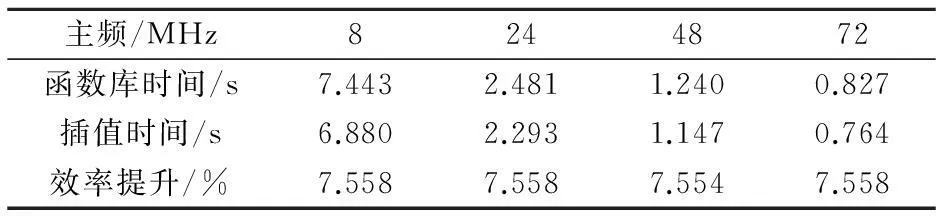
表1　不同主频下效率的提升(1)

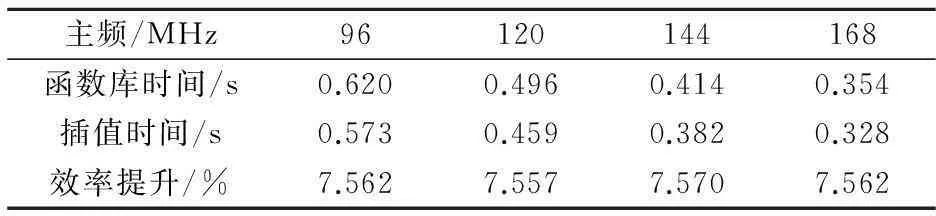
表2　不同主频下效率的提升(2)

根据C代码编译后的汇编语句，也可比较两者的效率，如图8所示，math.h中sinf函数编译后生成7条汇编指令，而arm_sin_f32函数编译后只有5条指令，说明在编译器的优化下，插值法编写的函数比函数库经过编译后会更精简、高效.

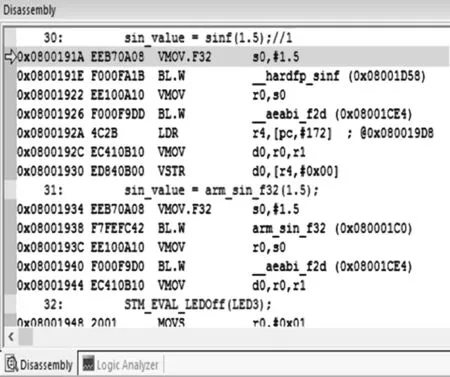
图8　两种方法下编译效率对比

其程序如下：

int main(void)

{

unsigned int Num=0;

SystemInit();//系统初始化

SystemCoreClockUpdate();//时钟

STM_EVAL_LEDOff(LED3);//输出低

STM_EVAL_LEDInit();

delay_ms(500);

STM_EVAL_LEDOn(LED3);

for(CirNum=0;Num<500000;Num++){

sin_value = sinf(1.5);

}

STM_EVAL_LEDOff(LED3);

STM_EVAL_LEDOn(LED4);

for(Num=0;Num<500000;Num++){

sin_value = arm_sin_f32(1.5);

}

STM_EVAL_LEDOff(LED4);

}

其中，STM_EVAL_LEDOn(LED3)为在LED3管脚输出高电平，采用库函数sinf计算500 000次后，执行STM_EVAL_LEDOff(LED3)后在LED3管脚输出低电平；STM_EVAL_LEDOn(LED4)为在LED4管脚输出高电平，采用库函数arm_sin_f32计算500 000次后，执行STM_EVAL_LEDOff(LED4)后在LED4管脚输出低电平.

3结论

通过上述大量实验可得出这样的结论：使用微控制器求解复杂函数值时，查表与插值法在处理器任何主频下、在不同编译效率的编译器下，均较直接调用编译器函数库的方式能更有效地提升处理器运算效率，经计算效率提升7.5%.处理器运算效率的提升具有现实意义.

同时，验证了该方法的可行性、通用性与高效性.虽然对微控制器的内存大小有一定要求，这是因为需要提前生成查询表，但是在测频、信号的采样与恢复、逆变器、电机控制和无线充电技术等领域内，所使用的微控制器大多数能达到这一要求，充分说明此方法具备可行性，后期可以通过适量的算法，在不影响功能的情况下减少内存使用，从而使内存使用、效率提升等更加均衡.

参考文献

[1] 刘小明,洪一.基于查找表和Taylor展开的正余弦函数的实现[J].现代电子技术,2009(13):165-170.

[2] 李善锋,刘敬猛,陈柏成,等.一种嵌入式NC代码编译器的设计[J].组合机床与自动化加工技术,2012(2)：45-48,53.

[3] 窦伟，黄念恙.单片机控制的正弦波逆变电源[J].电力电子技术,2004,38(6):94-96．

[4] 许玲，程小琰.C8051 F020单片机的特点及其在通信系统中的应用[J].河南机电高等专科学校学报,2006，14(6):15-16.

[5] 徐伟.一种在FPGA上实现32位浮点正弦函数的运算[J].山东理工大学学报(自然科学版),2008，22(3):93-96.

[6] 张月.插值算法在嵌入式系统中的应用[J].南京广播电视大学学报,2010(4):101-103.

[7] 刘云，应康，辛焕海,等.基于二次插值法的光伏发电系统控制策略[J].电力系统自动化,2012,36(21):29-35.

[8] 任红萍，程玉民，张武.改进的移动最小二乘插值法研究[J].工程数学学报,2010,27(6):1 021-1 029.

[9] 陈浩，华灯鑫，张毅坤，等.米散射激光雷达剖面数据三次样条垂直水平插值法[J].物理学报,2014,63(15):167-174.

[10] 陈东，张军明，钱照明.一种具有频率变化适应性的并网逆变器改进型重复控制方法[J].电工技术学报,2014,29(6):64-70.

[11] Smeti A.,Charga W.Implementation of a predictive controller on the STM32 board.control[J].Decision and Information Technologies,2013,21:250-253.

[12] 张雷，张国，邱亚琴.Lagrange 插值的改进算法研究及误差分析[J].电力系统保护与控制,2014,42(16):66-70.

[13] 郭乐，潘济猛，卢家力，等.插值算法在智能变电站中的应用[J].电力自动化设备,2010,30(10):103-109.

[14] 史文娇，岳天祥，石晓丽,等.土壤连续属性空间插值方法及其精度的研究进展[J].自然资源学报,2012,27(1):163-175.

Implementation of a look-up table and

interpolation in micro controller

SHI Yong-sheng， HU Shuang， XU Meng-yun， WANG Xi-feng

(College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China)

Abstract:A huge amount of computations with a long time are not desirable in micro controller interrupt program.In order to improve the computational efficiency,a method is proposed that calling the compiler function library for the complex function is changed into a look-up table and interpolation in the software.The introduction of the look-up table and interpolation method can improve the efficiency of the compiler in the program and the program′s execution speed in the micro controller,it has a high efficiency.In this paper, the micro controller STM32F407VGT6 is treated as the hardware platform,and it designs variable method of the contrast experiment.The results show that the method can effectively reduce the running time of the program, and it is suitable for most complex functions and micro controllers with different frequency,it verifies the method′s universality and high efficiency.

Key words:look-up table； interpolation； micro controller； caculating speed； caculating accuracy

中图分类号：TP311; TP332

文献标志码：A

文章编号：1000-5811(2015)02-0148-06

作者简介:史永胜(1964-)，男，陕西西安人，教授，博士，研究方向:开关电源与驱动技术、LED显示技术及新材料开发

基金项目：陕西省教育厅专项科研计划项目(12JK0494)； 陕西科技大学博士科研启动基金项目( BJ08-07)

收稿日期:*2014-11-29