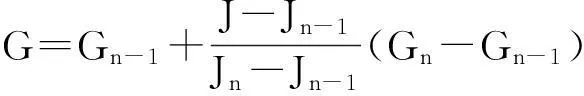考虑渗透率变化的低渗透油藏非达西渗流模型

李卫东, 吴亚芳, 马　哲, 苏玉亮

(1.延长油田股份有限公司 定边采油厂， 陕西 定边　718600； 2.中国石油大学(华东) 石油工程学院， 山东 青岛　266580)



考虑渗透率变化的低渗透油藏非达西渗流模型

李卫东1, 吴亚芳1, 马哲1, 苏玉亮2

(1.延长油田股份有限公司 定边采油厂， 陕西 定边718600； 2.中国石油大学(华东) 石油工程学院， 山东 青岛266580)

摘要：低渗透油藏流体的渗流为非达西渗流，常采用启动压力梯度来进行描述，但是实际渗流曲线却为非直线段.本文考虑了变化的渗透率和启动压力梯度，建立了低渗透油藏非达西渗流模型，保留二次项，并使用Newton-Raphson方法进行求解.计算结果表明：压力和压力导数曲线后半段出现上移，并且渗透率变化持续的时间越短，其所对应的启动压力梯度越大，则压力和压力导数曲线变化幅度越大；在圆形定压边界和封闭边界中，只有当外边界半径较大时，由渗透率变化引起的曲线上翘才更明显；相对于只考虑启动压力梯度的模型，本文模型曲线上翘幅度更小.

关键词：低渗透油藏； 渗透率变化； 非达西渗流； 启动压力梯度

0引言

大量实验证明,低渗透油藏中流体的渗流为非达西渗流，其渗流曲线为非直线段.目前,常用启动压力梯度来进行近似描述，如果要对地层渗流进行真实地反映，就必须使用曲线渗流规律[1-6].

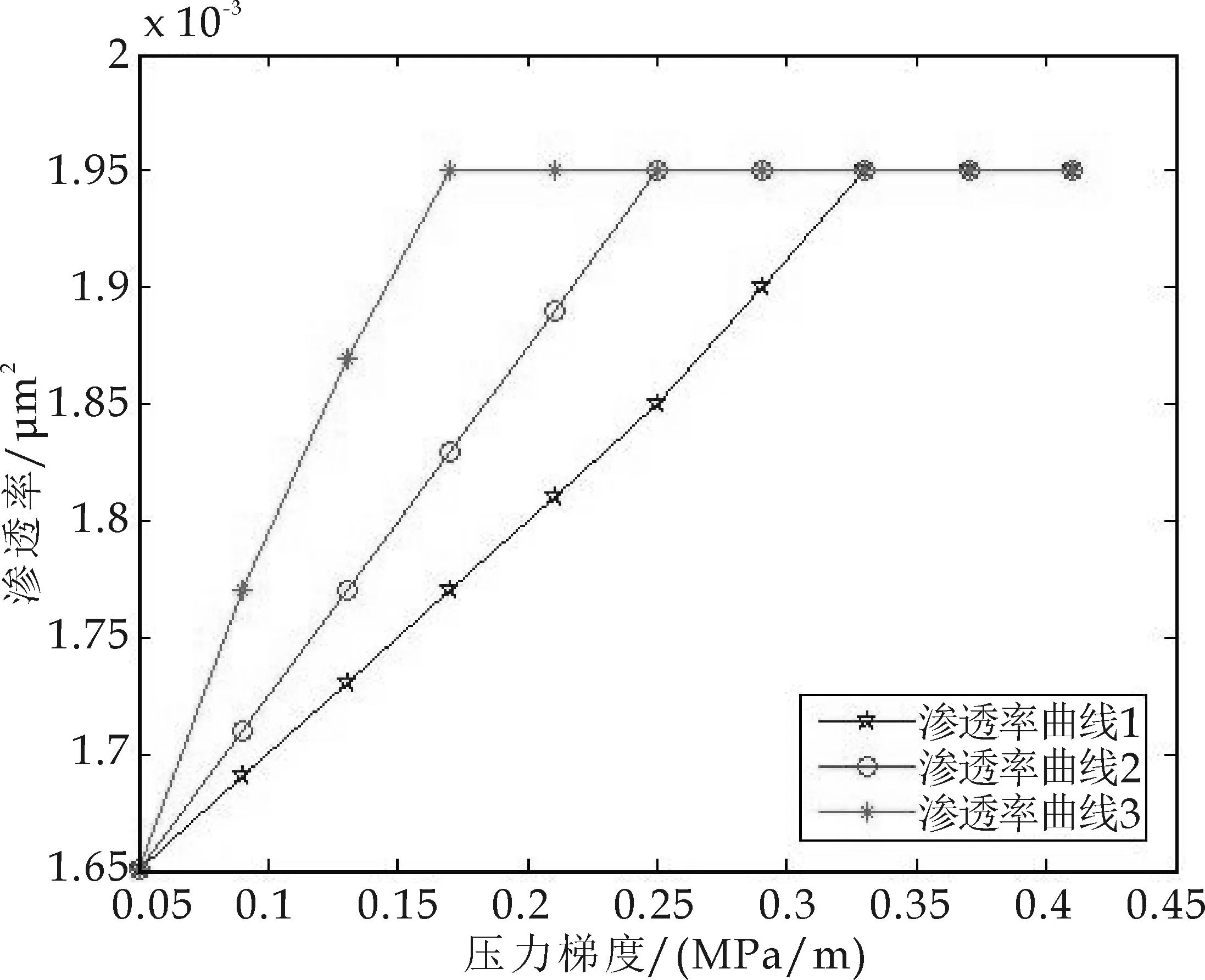
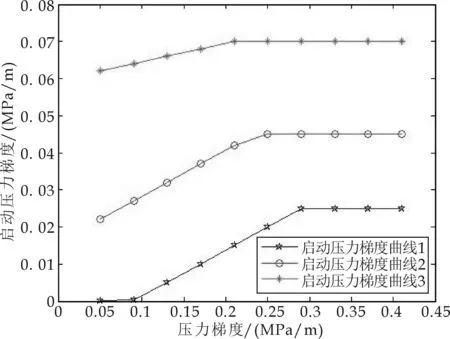
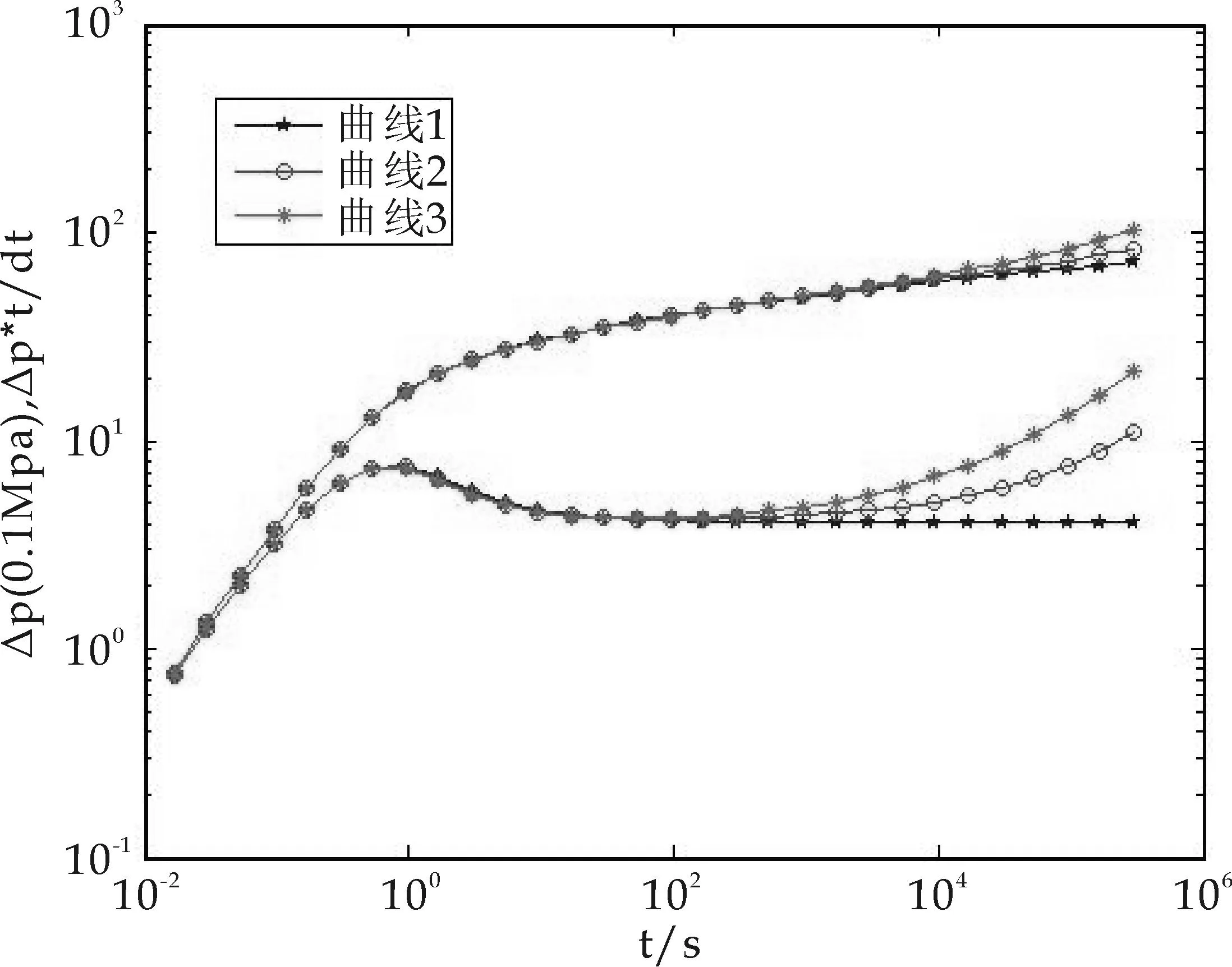
如图1所示，渗透率为渗流曲线上的点的斜率，启动压力梯度为其切线与压力梯度数据轴的交点.随着压力梯度的增加，斜率越来越大直至某一定值时就不再发生变化.这一现象称为渗透率的变化效应.

基于上述特征，本文建立了考虑井筒储存和表皮系数的低渗透油藏非达西渗流模型[7-14]，并运用Newton-Raphson方法进行了求解[15]，绘制了压力和压力导数曲线，并与常规模型进行了比较.

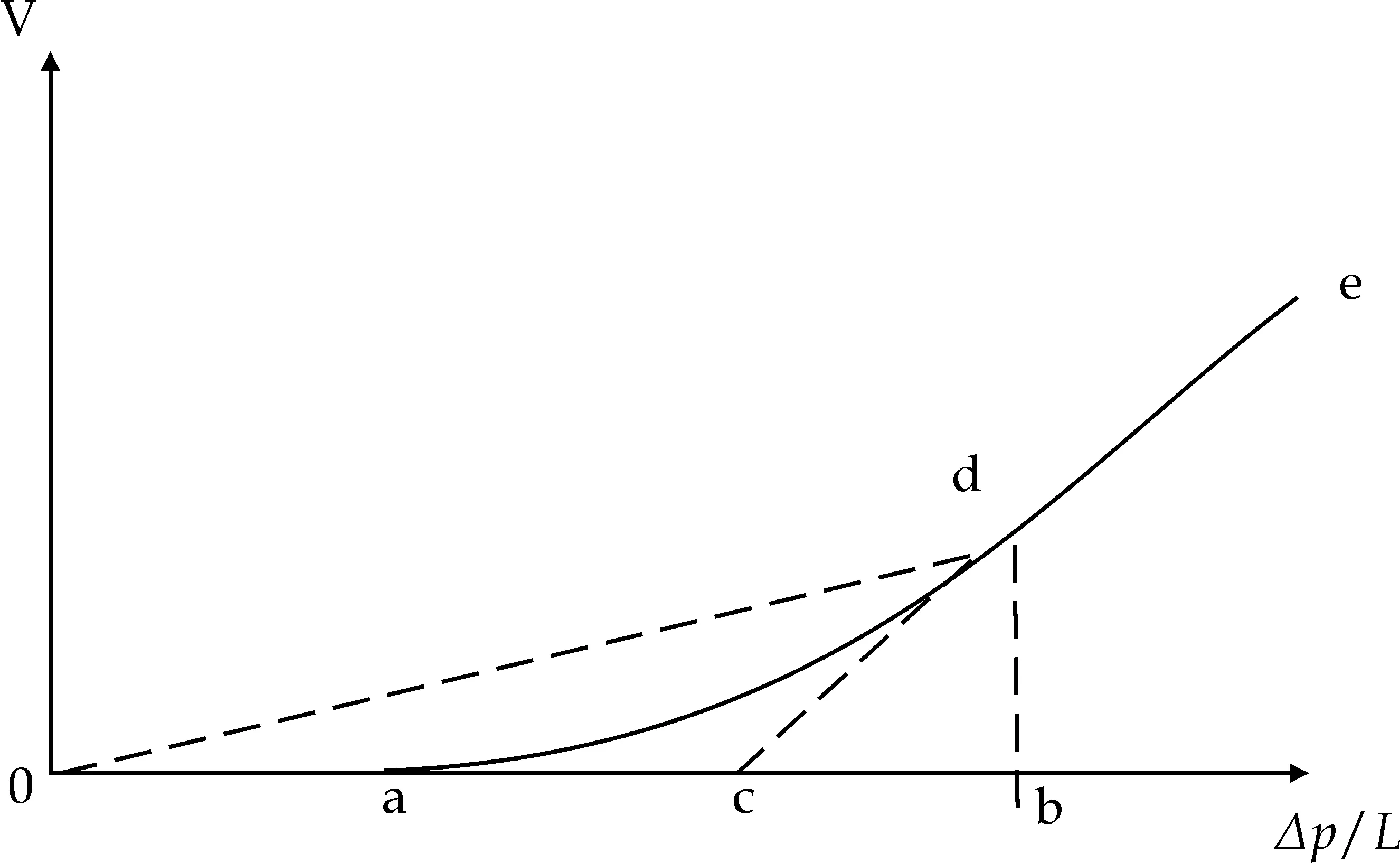
图1　原油非达西渗流示意图

1低渗透非达西模型的建立

1.1物理模型

对低渗油藏进行假设：(1)无限大地层中一口井以定产量进行生产；(2)储层等厚，各向同性，初始条件下压力分布均匀；(3)流体在地层中的流动不满足达西定律，并且流体微可压缩；(4)考虑表皮系数和井筒储存效应，并忽略重力和毛管力的影响.

1.2数学模型

(1)运动方程

考虑K和G随压力梯度的增加而增大，当压力梯度增大到某一临界值后，K和G将保持恒定.故运动方程如下：

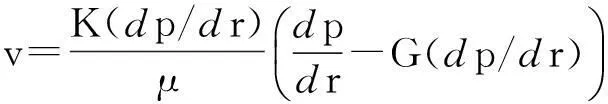
(1)

其中，v为渗流速度，K为渗透率，G是当渗透率为K时的启动压力梯度.

(2)状态方程

①岩石的状态方程

φ=φieCp(p-pi)

(2)

②液体的状态方程

ρ=ρieCl(p-pi)

(3)

(3)连续性方程

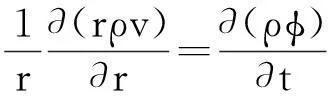
(4)

将式(1)～(3)代入式(4)中可得：

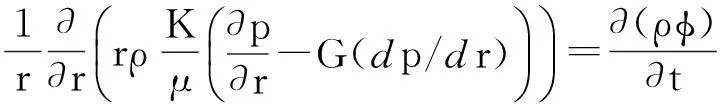
(5)

将式(5)展开并合并同类项，可得低渗透油藏非达西渗流模型为：

外边界条件：

上式中，p(r,t)为地层压力，MPa；pi为原始地层压力，MPa；pw为井底压力，MPa；K为地层渗透率，μm2；G为启动压力梯度，MPa/m；r为地层半径，m；Cl为流体压缩系数，MPa-1；Ct为综合压缩系数，MPa-1；μ为流体粘度，mPa·s；φ为孔隙度；rwe为有效半径,m;B为体积系数，m3/m3；q为日产油，m3/d；C为井筒储存系数，m3/MPa.

2低渗透非达西模型的求解

2.1模型的离散

本文采用无条件稳定的隐式差分方法对方程进行离散.在空间方向上采用向前差分，在时间方向上采用向后差分，二阶偏导数采用二阶中线差商.

首先,对近井地带网格进行加密，令：

x=ln(r/rwe)⟹r=rweex

(6)

将式(6)代入模型中进行转化，然后对渗流方程进行离散可得：

m=2,…,M-1,n=2,…,N.其中，M为空间方向上的节点数，N为时间方向上的节点数.

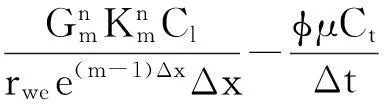
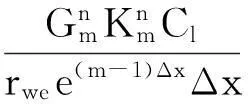
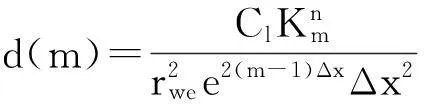
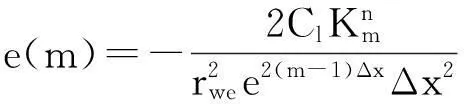
对内边界条件进行离散，得：

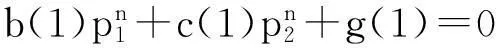
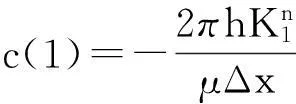
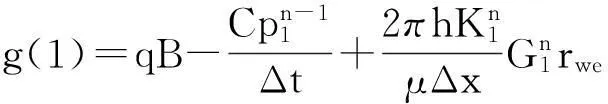
对外边界条件进行离散：

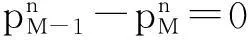
对初始条件进行离散可得：

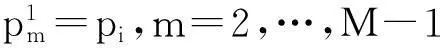
2.2模型的求解

(1)渗透率和启动压力梯度的计算

对K和G采用显式处理，根据上一时间步所计算的压力来计算下一时间步的K和G.

压力梯度的计算如下式表示：

如果，J所对应的K和G位于两个离散的K和G之间，即Jn-1

如果J≤Jmin，那么,K=Kmin,G=Gmin,

如果J≥Jmax，那么,K=Kmax,G=Gmax.

其中，Kmin和Kmax为渗透率的最小和最大值，Gmin和Gmax为与之对应的启动压力梯度值.

(2)方程组的解法

本文所得差分方程组具有强非线性特征，所以采用Newton-Raphson方法进行编程求解.在时间循环内，首先使用初始压力计算渗透率和启动压力梯度，然后代入差分方程组求解地层压力，再使用求得的地层压力计算渗透率和启动压力梯度，最后进入下一时间段的计算.

为了精确反映井筒储存阶段的压力变化，采用指数时间步长：

tn=0.01×100.025(n-1)

3参数敏感性分析

3.1渗透率和启动压力梯度的影响

由渗流曲线可得到渗透率随压力梯度变化的曲线,如图2所示；启动压力梯度随压力梯度变化的曲线如图3所示.

图2　渗透率随压力梯度变化曲线图

图3　启动压力梯度随压力梯度变化曲线图

由图4(S=3，C=0.1 m3/MPa)可以看出，压力和压力导数曲线在早期重合为斜率为1的直线;在中后期，压力和压力导数曲线均会出现上翘，其中渗透率变化持续的时间越短，对应启动压力梯度值越大，压力和压力导数曲线上翘时间越早，上翘幅度越大.

图4　压力和压力导数的双对数典型曲线图

3.2井筒储存系数的影响

从图5(曲线3，S=3)可以看出，压力和压力导数曲线随着C的增大平行右移，并且C越大，井筒储存阶段持续的时间变长.在井筒储存后期，压力导数曲线的“驼峰”随着C的增大而变高;在晚期，压力和压力导数曲线出现上翘，并且曲线相互重合，井底压力下降的速度和幅度相同.

图5　C影响的压力和压力导数双对数图

3.3表皮系数的影响

从图6(曲线3，C=0.1 m3/MPa)可以看出，压力导数曲线上的“驼峰”会随着表皮系数的增大而变高.其峰值越高，表示井筒周围受污染越严重.在晚期，压力和压力导数曲线出现上翘，并且压力下降的速度相同.

图6　表皮系数影响的压力和压力导数双对数图

3.4 封闭外边界的影响

从图7(曲线3，S=3,C=0.1 m3/MPa)可以看出，压力和压力导数曲线在早中期分别重合在一起，后期拟稳态流动阶段，压力和压力导数曲线上翘重合为斜率为1的直线，并且直线段随着边界距离的增大而平行右移.封闭油藏外边界半径越小，压力特征曲线上翘越早.

图7　封闭边界影响的压力和压力导数双对数图

3.5定压外边界的影响

从图8(曲线3，S=3,C=0.1 m3/MPa)可以看出，后期拟稳态流动阶段，各压力曲线变为水平的直线段，达到定压边界；由于压力逐步趋于稳定，所以压力导数会出现“下掉”.边界距离越大，水平直线段出现得越晚，即压降漏斗传到边界需要的时间越长.同时，边界距离越大，压力导数曲线的“下掉”出现得也越晚.

图8　定压边界影响的压力和压力导数双对数图

3.6不同方法的对比

对油藏采用三种方法计算其压力响应.这三种方法分别为：

(1)不考虑启动压力梯度的方法.此时认为K=4.3×10-3μm2，G=0 MPa/m.

(2)只考虑启动压力梯度方法.此时认为K=4.3×10-3μm2，G=0.044 MPa/m.

(3)考虑渗透率变化的方法.此时认为K=(0～4.3)×10-3μm，G=(0～0.044) MPa/m.计算的结果如图9和图10所示(S=3，C=0.1 m3/MPa).

从图9可以看出，对于无限大油藏，考虑渗透率变化的模型，其压力及压力导数曲线上翘的幅度比带启动压力梯度模型上翘的幅度小且平缓，符合实际情况.

图9　无限大油藏下压力和压力导数双对数图

从图10可以看出，对于封闭外边界油藏，考虑渗透率变化使得压力导数曲线上翘的幅度比封闭边界效应引起的上翘幅度要小且出现时间早，两者有着明显的区别.

4结论

(1)在低渗透油藏中，考虑渗透率的变化，建立了低渗透油藏非达西渗流模型.对于模型的非线性特征，使用Newton-Raphson方法进行了求解.

(2)本文模型压力和压力导数曲线后期出现上移，渗透率变化持续的时间越短，启动压力梯度越大，则曲线上移就越明显.

(3)考虑渗透率变化的模型，压力和压力导数曲线的上翘幅度比只考虑启动压力梯度的模型要小而且平缓，并且与封闭边界所引起的曲线上移有明显区别.

(4)封闭边界和定压边界的外边界半径越大，则由渗透率变化引起的导数曲线上移越明显.

参考文献

[1] 郑春峰，程时清,李冬瑶.低渗透油藏通用非达西渗流模型及压力曲线特征[J].大庆石油地质与开发，2009，28(4)：61-63.

[2] 曹维政，肖鲁川，曹维福,等.特低渗透储层油水两相非达西渗流特征[J].大庆石油地质与开发，2007,26(5)：61-63.

[3] 李中锋，何顺利.低渗透储层非达西渗流机理探讨[J].特种油气藏，2005,12(2)：35-38.

[4] 成绥民，甘庆明，成珍,等.低渗油藏非线性渗流压力分析[J].油气井测试，2005，14(3)：1-4.

[5] 姚约东，葛家理.低渗透油藏不稳定渗流规律的研究[J].石油大学学报(自然科学版)，2003,27(2):55-58,62.

[6] 同登科，张海英.变形双重介质分形油藏渗流流动分析[J].石油大学学报(自然科学版)，2003，27(4)：76-79.

[7] 赵冬梅，姚军,王子胜.压敏三重介质油藏压力响应特征[J].计算物理，2005，22(5)：444-448.

[8] 杨蕾，林红.应力敏感低渗复合油藏试井模型[J].西部探矿工程，2006(2)：73-74.

[9] 马骁丹，同登科,马华伟.变形双重介质分形油藏非达西流动分析[J].计算物理，2007，24(2)：197-202.

[10] 张允，王子胜,姚军,等.带启动压力梯度的双孔压敏介质压力动态及其应用研究[J].水动力学研究与进展A辑，2007，22(3)：332-337.

[11] 王喜红.低渗透油藏试井分析方法研究[D].青岛：中国石油大学(华东),2010.

[12] 李淑霞，谷建伟.油藏数值模拟基础[M].青岛：中国石油大学出版社，2008.

[13] 郭永存，卢德唐，马凌霄.低渗透油藏渗流的差分法数值模拟[J].水动力学研究与进展A辑，2004,19(3):288-293.

[14] 张艳玉，姚军.现代试井解释原理与方法[M].东营：中国石油大学出版社，2006.

[15] 戴嘉尊，邱建贤.微分方程数值解法[M].南京：东南大学出版社，2002.

Non-darcy flow model of low-permeability reservoirs

considering permeability changes

LI Wei-dong1， WU Ya-fang1， MA Zhe1， SU Yu-liang2

(1.Dingbian oil production plant of Yanchang Oil Field Corporation Limited, Dingbian 718600, China; 2.School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China)

Abstract:The flow of low-permeability fluid is non-darcy flow,often be described by start-up pressure gradient,but the actual percolation curve is not straight line.This paper considering changed permeability and start-up pressure gradient,the non-darcy flow model was established,retain the two items,solve the model by Newton-Raphson method.The result is that the log-log pressure and derivative curves will upward in the later period,the lasting time of changing permeability was shorter and start-up pressure gradient was larger,the log-log pressure and derivative curves were more upward;In the closed boundary and constant pressure boundary，when outer boundary radius was bigger,the log-log curves were more upward;the upward of this model′s curves is smaller than others.

Key words:low-permeability reservoirs； permeability changes； non-darcy flow; start-up pressure gradient

中图分类号：TE348

文献标志码：A

文章编号：1000-5811(2015)02-0111-05

作者简介:李卫东(1987-)，男，陕西咸阳人，助理工程师，硕士，研究方向：油气渗流理论及应用

基金项目：国家科技部重点基础研究发展规划“973”计划项目(2006CB705804)

收稿日期:*2015-01-13