基于响应面法的印制电路板组件有限元模型修正

2016-01-11王开山,李传日,庞月婵等

振动与冲击 2015年22期

王开山，李传日，庞月婵，郭恒晖

(北京航空航天大学可靠性与系统工程学院，北京100191)

摘要：在将印制电路板及元器件材料视为正交各向异性前提下，提出基于响应面法的印制电路板组件(Printed Circuit Board Assembly，PCBA)有限元模型修正法。利用相关性分析筛选出对PCBA模态频率影响较大参数作为修正参数；据修正参数数目选择合适的试验设计获取样本点，构造多项式响应面模型；通过最小二乘法确定多项式系数并检验响应面拟合精度；用响应面计算结果与模态试验结果误差绝对值构造目标函数；通过多目标遗传算法(MOGA)迭代计算获得优化修正参数并代入有限元模型获得修正模型。以某航空电子产品某PCBA为案例，对比修正前后各阶模态频率与试验值误差。结果表明，修正后模型各阶模态频率与试验值相对误差均明显减小，验证该方法对PCBA模型修正的有效性。

关键词：各向异性；印制电路板组件；模型修正；相关性分析；响应面法；优化求解

中图分类号:V414；TB330.1；TH113文献标志码：A

基金项目：国家自然科学基金资助项目(51175086)；福建省自然科学

收稿日期：2014-08-19修改稿收到日期：2014-10-23

Finite element model updating of printed circuit board assembly based on response surface methodology

WANGKai-shan,LIChuan-ri,PANGYue-chan,GUOHeng-hui(Beijing University of Aeronautics and Astronautics, School of Reliability and Systems Engineering，Beijing 100191, China)

Abstract:On the premise of taking the materials of the printed circuit board and its components as orthotropic, a method based on response surface was proposed to update the finite element model(FEM) of printed circuit board assembly(PCBA). The parameters which have great influence on the modal frequencies of PCBA were screened out and taken as the updating parameters by correlation analysis. The sample points were acquired by using an appropriate experimental design according to the number of the updating parameters to construct a polynomial response surface model. The least squares method was used to determine the polynomial coefficients and then to test the fitting accuracy of response surface. The absolute value of error between the result of the calculated response surface and that of an actual test was taken as an objective function. The optimized parameters were obtained taking advantage of the iterative calculation of the multiple objectives genetic algorithm (MOGA). The updated model was then obtained by substituting the optimized parameters into the non-updated FEM. Taking the PCBA of an aircraft electronic product as an example, the comparison between the modal frequencies of non-updated and updated FEM shows that the relative error of modal frequencies of the updated FEM to the actual test is obviously reduced and thus verifies the effectiveness of the model updating methodology suggested.

Key words:orthotropic; printed circuit board assembly(PCBA); model updating; correlation analysis; response surface methodology; optimization

振动会造成电子产品发生故障，尤其对机载电子产品，在寿命周期内需经受严酷的动力学环境，致故障更严重。为提高电子产品可靠性，须增强其抗振能力。有限元仿真因周期短、成本低等优势已成为产品动力学分析的重要方法。对产品进行有限元仿真前需进行实物模态试验作为仿真结果检验及模型修正标准。模态试验时通常无法将PCB与元器件分开，只能对装配体即PCBA进行整体试验，使对应的PCBA有限元模型精度非常重要。

工程实践中通常按各向同性给出PCB及元器件材料参数的经验值[1-2]，但其仿真结果往往与模态试验结果相差较多。因不同PCB板铺层、工艺不同材料参数有差异；元器件材料参数因器件种类、封装不同存在较大不同。即使同一块PCB板也会因不同位置电路、通孔分布表现出材料参数的各向异性。为提高仿真精度，需将PCB及元器件材料视为各向异性对PCBA模型进行修正。

响应面法因具有易于迭代、优化特点广泛用于结构优化设计。因此利用该方法进行动力学模型修正的研究成为热点。鲍诺等[3]利用响应面法对欧洲航空科技组织的基准GARTEUR飞机模型进行修正。费庆国等[4]在响应面方法基础上结合软件MATLAB与ANSYS的集成实现钢架结构模型修正。常涛等[5]利用响应面法对PCB裸板进行模型修正。而对工程遇到最多的PCBA模型修正研究尚处空白。本文在响应面方法基础上，结合相关性分析及优化算法给出PCBA模型修正的一般流程及方法原理，并以某航空电子产品某PCBA为算例，验证该方法的合理性及有效性。

1PCBA模型修正流程

PCBA有限元模型修正的一般流程见图1。包括参数筛选、响应面模型构建及优化求解三大模块。所涉关键技术方法有相关性分析、试验设计、响应面拟合、拟合优度检验及遗传算法等。

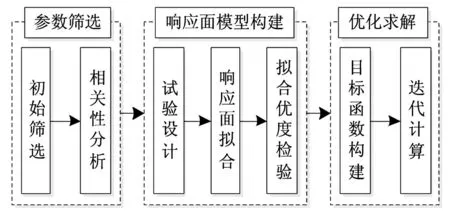
图1　PCBA模型修正流程 Fig.1 The model updatingprocess of the PCBA

2修正参数筛选

2.1参数初始筛选

对输出响应量，因模态频率易测量、精度高，故本文选前三阶模态频率作为响应特征量。影响PCBA模态频率因素有模型的几何尺寸参数、密度及材料参数[6]。几何参数、密度易控制及测量，波动性不大；材料参数由铺层、工艺、电路分布、通孔分布等不同导致的不确定性较大为造成PCBA动力学仿真结果不准确的主要因素[7-8]。据此将PCB及元器件材料参数作为初始筛选参数，包括PCB、元器件各自三个轴向弹性模量、平面泊松比及平面剪切模量计18个参数。并将其视为正交各向异性；对元器件，封装种类不同其材料参数亦不同。本文为简化仅考虑器件均塑料封装情况，将所有元器件视为同种材料进行处理。

2.2相关性分析

初始筛选的18个参数均波动性较大，但并非所有参数均对输出参数(前三阶模态频率)产生较大影响，需定量相关性分析,筛选对模态频率影响大的参数。Speraman等级相关系数可从全局角度考量输入对输出的相关性，计算式为

(1)

式中：R(xi)为将不确定参数抽样值(x1,x2,…,xn)按升序或降序排列时xi的排序号；R(yi)为将响应计算值(y1,y2,…,yn)按升序或降序排列时yi的排序号；n为抽样次数。

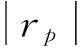
3响应面模型构建

多项式响应面为用统计学回归分析进行函数拟合的近似方法，通过确定性试验设计拟合出响应面函数近似模拟真实输入、输出间隐式关系，使系统分析可建立在响应面函数上。与一次、高次(三次及以上)响应面相比，二次响应面能较权衡近似精度与计算量间的矛盾，故工程中应用较广[11-13]。

3.1试验设计

基于多元线性回归的多项式响应面需数据样本，构造的样本试验点在修正参数区间内分布对响应面近似精度影响较大。全因子设计将每个因素的不同水平组合均进行一次试验，因该方法为因子与水平的完全组合，结果真实可靠；但计算量过大只适合因素较少情况[14]。因素较多时常采用中心点复合设计、Box-Behnken Design及D-最优设计等，均能用最少试验样本点获得理想的响应面模型[15]。

3.2响应面拟合

PCBA前n阶仿真模态频率y为因变量，xi(i=1,2,…,k，k)为修正参数个数。多项式响应面函数表示为

(2)

式中：xi∈[xil,xiu]，xil,xiu分别为修正参数xi取值上下限；β0,βi,βij,βii为待定系数[16-17]。

可将试验样本点代入函数方程用最小二乘法估计多项式系数β0,βi,βij,βii。

3.3拟合优度检验

利用相对均方根误差RMSF及R2判断系数法可定量检验响应面精度，计算式为

(3)

4优化求解

模型修正问题转化为多目标优化问题，即

(4)

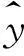
采用多目标遗传算法(MOGA)对构建的目标函数进行迭代计算获得修正后参数，代入有限元模型计算可得修正后模型。

5案例分析

所选案例为某航空电子产品中某PCBA，实物见图2(a)。在不影响产品动力学特性前提下，在CAD软件中按原则对该PCBA的数字样机进行必要简化，见图2(b)。遵循原则为，①去掉尺寸较小的孔；②去掉尺寸较小的凸台；③去掉尺寸较小的圆角；④去掉不必要的倒角；⑤适当省略对整体PCBA模态特性影响较小的小体积及小质量器件。

图2　PCBA实物及有限元模型 Fig.2 The physical model and finite element modelof the PCBA

5.1模态试验及初始仿真

对PCBA进行自由状态模态试验，提取前三阶频率；在ANSYS中按各向同性给出PCB及元器件材料参数的经验值，边界条件设为自由状态，选择合适的网格划分形式划分网格后进行初始仿真，初始材料参数见表1。初始仿真与模态试验结果对比见表2。由表2看出，初始仿真与试验结果误差较大，需进一步修正。

表1　初始材料参数

表2　初始仿真与试验结果对比

5.2参数筛选

将PCB与元器件材料视为正交各向异性，计算前三阶模态频率与18个参数的Speraman等级相关系数，结果见图3。由图3看出，前三阶模态频率与印制电路板Y向弹性模量P-Ey、印制电路板XY平面的剪切模量P-σxy及元器件XY平面剪切模量C-σxy的相关性超过0.3，因此将其确定为修正参数。

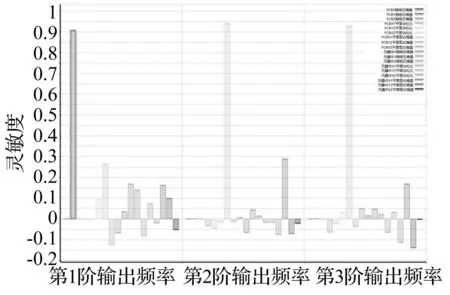
图3　相关性分析结果 Fig.3 The results of correlation analysis

5.3响应面模型构建

修正参数仅3个，用全因子方法进行试验设计。每个因素取3个水平，所选水平值需能覆盖其整个区间，3个因素所选3个水平为：P-Ey为6.5E+9、8.75E+9、1.1E+10；P-σxy为1E+9、2.648E+9、4.297E+9；C-σxy为3E+8、2.45E+9、4.6E+9；共进行27次有限元仿真试验，每组试验只改变修正参数值，控制边界条件及网格划分等设置条件与初始仿真一致，即边界条件均为自由状态，网格数均为8 244；将试验所得样本点归一化后代入响应面方程，用最小二乘法估计出多项式系数。构建的前三阶响应面方程为

(5)

取13个样本点进行拟合优度检验，计算R2判断系数及相对均方RMSE，结果见表3。R2趋近1表明响应面与真值之间差异程度小；RMSE趋近0表明响应面精度高。

表3　R 2及RMSE检验

5.4优化求解

用前三阶模态频率与试验值的误差绝对值构造三个目标函数，采用MOGA遗传算法迭代计算获得优化修正后参数，并与初始参数对比见表4。将修正后参数代入有限元模型计算获得修正后模型，仿真与试验值对比见表5。

表4　模型修正前后参数对比

表5　模型修正后仿真与试验结果对比

模型修正前后模态频率相对误差对比见表6，MAC值对比见表7。由表6知，修正后各阶仿真模态频率与模态试验各阶结果相对误差均明显减小。由表7知，修正后各阶MAC值均较修正更接近1，从而验证基于响应面法对PCBA模型修正的合理性及有效性。

表6　模型修正前后相对误差对比

表7　模型修正前后MAC值对比

6结论

(1)基于相关性分析、响应面拟合及优化求解相结合方法可准确对PCBA模型进行修正，有效提高模型精度；用响应面替代真实模型进行动力学模型修正可避免多次调用有限元程序，提高分析效率。

(2)本文将所有元器件按同一种材料处理，但实际上不同种类元器件材料参数差异较大，可对不同种类元器件分别定义为不同变量进行分析修正效果可能更好。

参考文献

[1]王红芳，赵玫．基于动态特性的印制板结构改进[J]．振动与冲击,2000,19(1):49-51.

WANG Hong-fang, ZHAO Mei. The structure improvements based on the dynamic characteristics of the printed circuit board[J]. Journal of Vibration and Shock, 2000, 19(1): 49-51.

[2]杨宇军,叶松林,游少雄,等．插板式PCB的内置式减振设计方法及其PSD动力学仿真[J]．振动与冲击，2007，26(2)：39-42.

YANG Yu-jun, YE Song-lin, YOU Shao-xiong, et al. The vibration damping design method of PCB and its PSD dynamics simulation[J]. Journal of Vibration and Shock, 2007, 26(2): 39-42.

[3]鲍诺,王春洁,赵军鹏,等．基于响应面法的结构动力学模型修正[J]．振动与冲击,2013,32(16):30-34.

BAO Nuo,WANG Chun-jie,ZHAO Jun-peng,et al.The structural dynamics model updating based on response surface methodology[J].Journal of Vibration and Shock,2013,32(16):30-34.

[4]费庆国,韩晓林,苏鹤玲．响应面有限元模型修正的实现与应用[J]．振动、测试与诊断,2010,30(2):132-134.

FEI Qing-guo, HAN Xiao-lin，SU He-ling. The implementation and application of finite element model updating based on response surface[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(2): 132-134.

[5]常涛,郭勤涛,张保强．应用模型修正方法的印制电路板参数识别[J]．振动、测试与诊断，2013，33(3)：111-116.

CHANG Tao, GUO Qin-tao, ZHANG Bao-qiang. Parameter identification of printed circuit board using model correction method[J]. Journal of Vibration，Measurement & Diagnosis, 2013,33(3):111-116．

[6]Heinonen O, Pajunen S. Optimal design of stiffened plate using metamodeling techniques[J]. Journal of Structural Mechanics, 2011, 44(3): 218-230.

[7]Friswell M I, Mottershead J E, Ahmadian H. Combining subset selection and parameter constrants in model updating[J]. Journal of Vibration and Acoustics, 1998, 120(4): 854-859.

[8]Friswell M I, Garvey S D, Penny J E T. The convergence of the iterated IRS method[J]. Journal of Sound and Vibration, 1998, 211(1): 123-132.

[9]庄楚强．应用数理统计基础(4版)[M]．广州:华南理工大学出版社,1992.

[10]Dougles C. Montgomery design and analysis of experiments [M]. John Wiley & Sons, Tnc, 2008.

[11]郭勤涛,张令弥,费庆国．用于确定性计算仿真的响应面法及其试验设计研究[J]．航空学报,2006,27(1): 55-61.

GUO Qin-tao, ZHANG Ling-mi, FEI Qing-guo. Response surface method and its experimental design for deterministic computer simulation[J]. Journal of Aeronautics,2006,27(1):55-61.

[12]宗周红,高铭霖,夏樟华．基于健康监测的连续刚构桥有限元模型确认(I)-基于响应面法的有限元模型修正[J]．土木工程学报,2011,44(2)：90-98.

ZONG Zhou-hong, GAO Ming-lin, XIA Zhang-hua. The finite element model validation of continuous rigid frame bridge based on health monitoring(I)-the finite element model updating based on response surface[J]. China Civil Engineering Journal, 2011, 44(2): 90-98.

[13]Kwon J H, Hwang S M, Lee C M, et al. Application of response surface methodology in microspeaker design used in mobile phones[J]. Institute of Electrical and Electronics Engineers Transactions on Magnetics, 2009, 45(10): 4550-4553.

[14]Montgomery D C. Design and analysis of experiments [M]. John Wiley & Sons, Tnc, 2008.

[15]Montgomery D C．试验设计与分析[M]．北京：中国统计出版社,1998:563-575.

[16]费庆国,张令弥,李爱群,等．基于统计分析技术的有限元模型修正研究[J]．振动与冲击,2005,24(3):23-26.

FEI Qing-guo, ZHANG Ling-mi, LI Ai-qun, et al. The finite element model updating based on statistical analysis techniques[J]. Journal of Vibration and Shock,2005,24(3): 23-26.

[17]费庆国，韩晓林，苏鹤玲．响应面有限元模型修正的实现与应用[J]．振动、测试与诊断,2010,30(2)：132-134.

FEI Qing-guo, HAN Xiao-lin, SU He-ling. The implementation and application of finite element model updating based on response surface[J]. Journal of Vibration, Measurement & Diagnosis,2010,30(2):132-134.