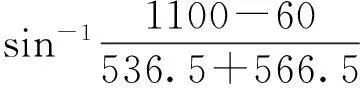滚筒式切头飞剪机剪切工艺过程分析
2016-01-09柳冉,高玉田,潘纪根等
滚筒式切头飞剪机剪切工艺过程分析
柳冉1,高玉田2,潘纪根2,付江2
(1.中国重型机械研究院股份公司,陕西 西安 710032;2.上海宝山钢铁集团公司,上海 201900)
摘要:分析了滚筒式热板坯切头飞剪机的“自然位移”参数(Δz、hj);确定出不定积分常数Cj,平移自然位移剪刃侧间隙曲线族,得出了剪切工艺过程剪刃侧间隙恒定的结论。进而阐明了上下剪刃位移间隙的连续可调性,可调双向性。并确定了热板坯的断裂“区”、“点”及其有关问题等。
关键词:切头飞剪;自然位移;剪切工艺;侧间隙
中图分类号:TG333文献标识码:A
收稿日期:2015-02-16;修订日期:2015-03-24
作者简介:柳冉(1937-),男,“外耦滚筒机构协衡飞剪机”科研项目总设计师,该项目获“世界知识产权组织中国发明专利金奖、国家香港《刘永龄科技奖》、 1999 年度国家机械工业局科技进步特等奖, 1999 年度上海市优秀发明一等奖, 2000 年度国家科技进步二等奖”等九项大奖。枊冉在《钢铁》、《机械工程学报》、《重型机械》等杂志发表论文十几篇。
Cutting process analysis of rotary
LIU Ran1, GAO Yu-tian2, PAN Ji-gen2, FU Jiang2
(1.China National Heavy Machinery Research Institute Co., Ltd., Xi’an 710032,China;
2.Baosteel Co., Ltd.,Shanghai 201900,China)
Abstract:This paper analyzed the natural displacement parameter Δz、hj, determined indefinite integral constant cj and curves of panning natural displacement gap part, and obtained a conclusion that natural displacement gap constant invariableness. Additionally, displacement gap could continuous adjusted and a two-way adjustment is feasible. While crack area and point and other relative issue were determined.
Keywords:

0前言
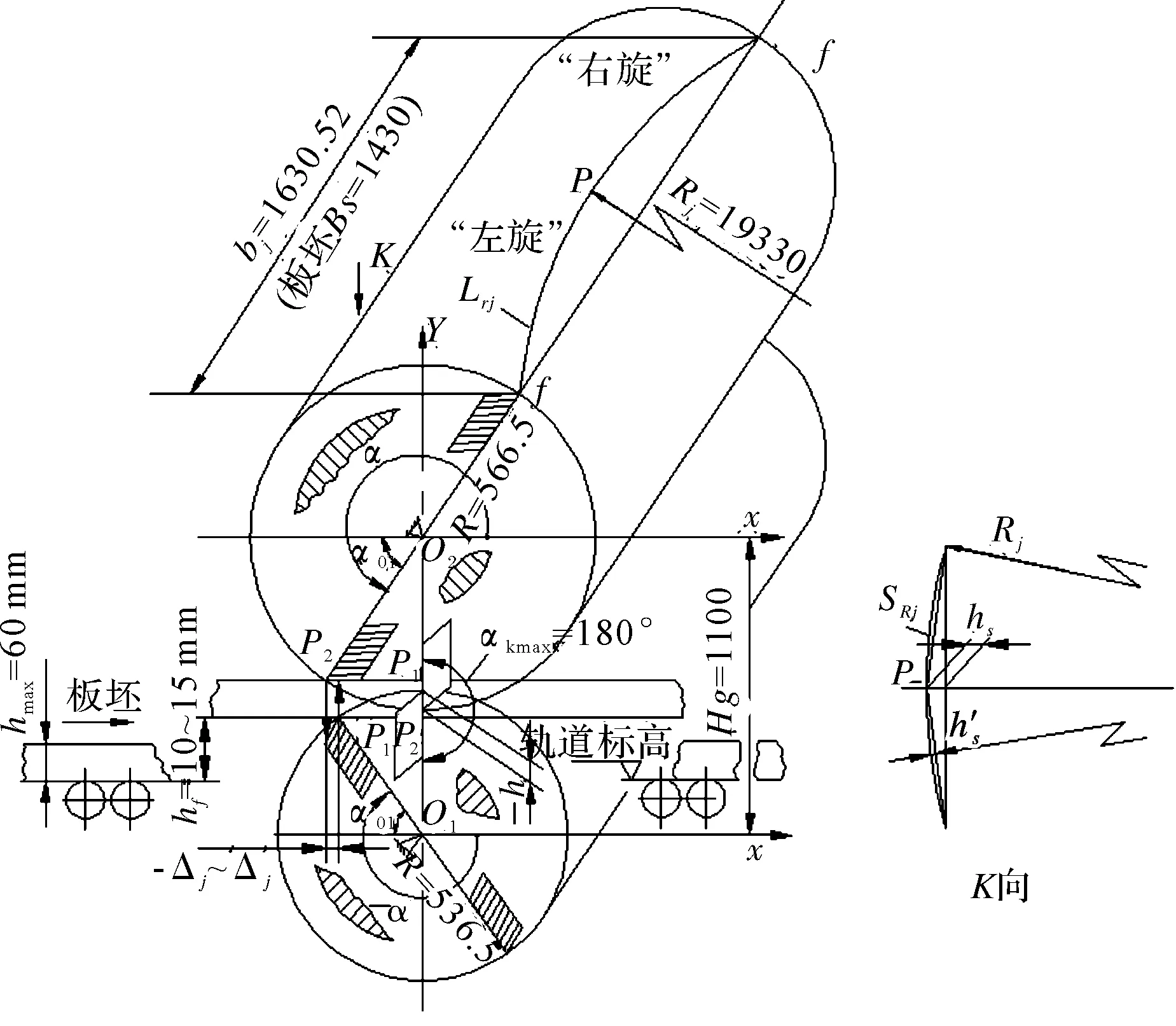
热板坯平面圆弧头曲线SRj与滚筒体剪刃空间类螺旋线LRj的加工关系在原理上是复杂的。切头飞剪是粗糙的中间工艺设备,须采取简化技术方为可行设计。其简化点之一是取LRj的曲率半径Rj=19 330 mm。这样LRj在板坯平面上的展开曲线SRj从其中央1点P等分为左、右两半时,等分后的弧长与弦长的绝对差值很小,其相对差趋于零(图1K向)。例如宝钢滚筒切头飞剪的绝对差为0.06 mm,相对差为0.074‰⟹0。以弦代替弧进行分析,不会失去计算精度。
事实上切头飞剪机示意图1的上下剪刃任意对应1点的位移原理,与老式滚筒飞剪的上、下平行直线剪刃,O1、O2共y轴线,原始刀面扩展角αk max=180°等确定机构参数的特征条件相同。因此在给定转角α区间内,公式(7)剪刃侧间隙位移固有余弦函数曲线Δz(α)在数理上满足平移条件。切头飞剪的创新点,在于沿y轴平移了两次Δz(α)曲线,是必须的和充分的。但是在已有文献中未见提出这个问题。
若以下剪刃半径R1为主导。切头飞剪分为R1
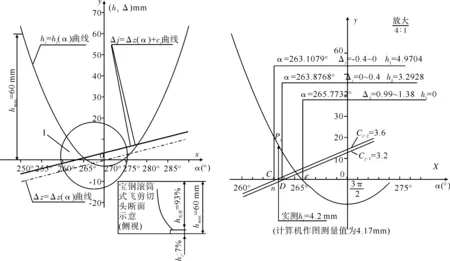
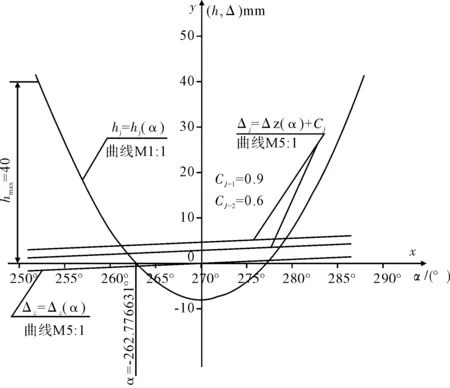
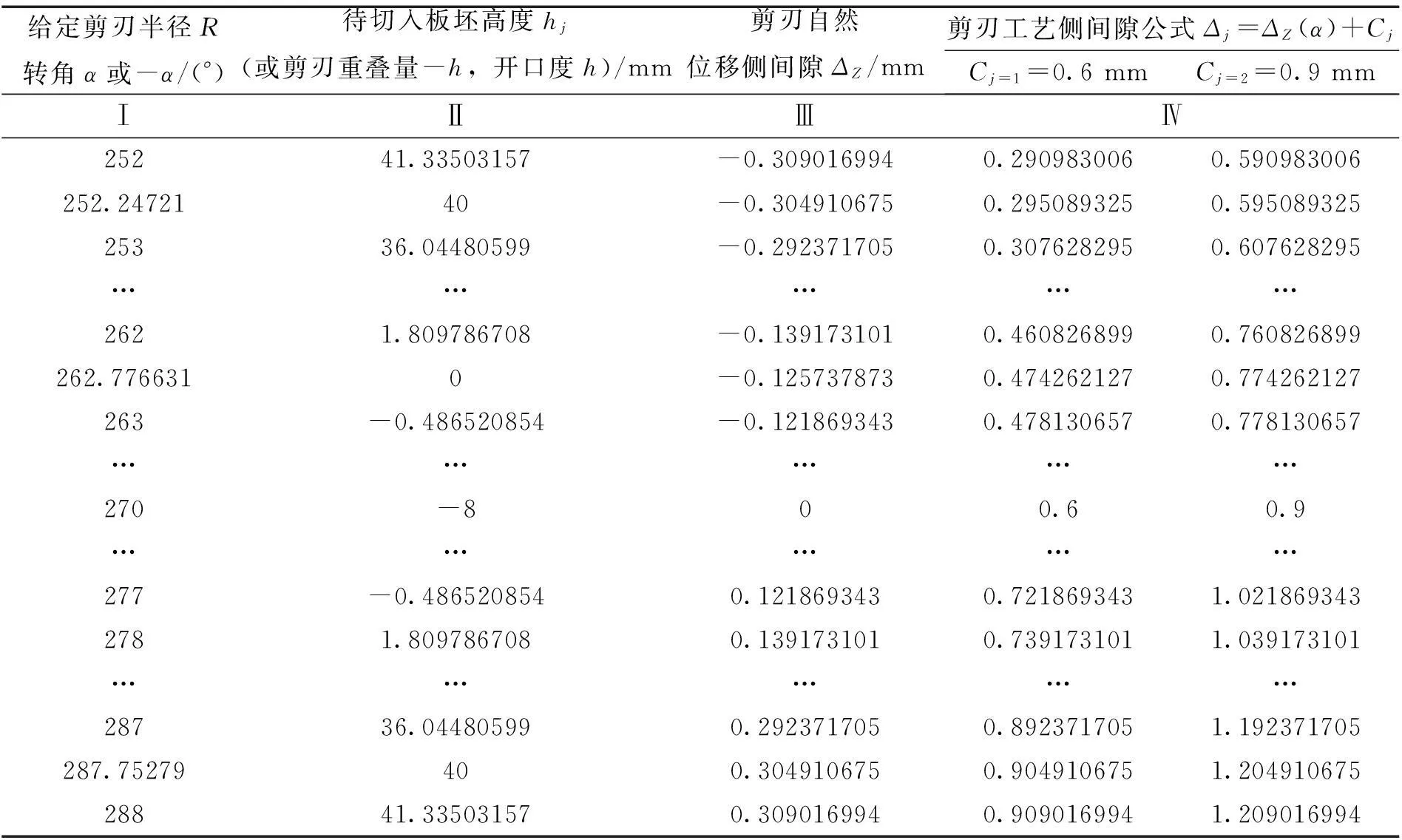
1宝钢滚筒式切头飞剪机R1 切头飞剪上下滚筒体都由速比i=1的齿轮进行了刚性联锁,那么R1≠R2的上下剪刃如何同时接触板坯最大厚度hmax须进行计算确定。令图1(图中数据为宝钢切头飞剪值,摘自文献[6])中,α01为同时接触角,则: 图1 宝钢切头飞剪机机构参数 Fig.1 Cutting head shear mechanism parameter of Baosteel (1) 由α01决定位移区间的起点。将α01+180°=±α为以X轴的计数角。±号如图1所示。在板坯温度870 ℃ hj=Hg-(R1+R2)×sin±α (2) Δz=(R2-R1)×cos±α (3) 计算结果列在表1中,据此作出图2的hj(α)和Δz(α)两条曲线。由表1和图2看出,剪切段限定区间250°≤α′≤265.77°。其下限仅差0.23°的α=266°时,hj=-0.31 mm,Δz=-2.09 mm,就是上下剪刃的严重刚性碰撞和干涉。自然位移过程不能用于生产。 公式(2),(3)的hj(α)和Δz(α)都是原函数。根据不定积分定义,沿图2 Y轴正方向平移Δz(α)曲线(hj(α)是不可平移性曲线)。即令剪切工艺侧间隙平移公式为 表1 宝钢切头飞剪机 R 1< R 2位移参数计算表 Δj=Δz(α)+Cj (4) 式中,Δz(α)由公式(3)求得,C下标j为自然数,根据不定积分定理,常数Cj取不同值时,Δz(α)+Cj都是不同的原函数(原函数族)。只要两个原函数导数之差 [Δz(α)+Cj=2]′-[Δz(α)+Cj=1]′= Δz′(α)-Δz′(α)=0 根据微分应用《定理》,在给定α角区间内,二原函数之差 [Δz(α)+Cj=2|-|Δz(α)+Cj=1]=常量 (5) 图2 宝钢滚筒式切头飞剪机R 1 公式(7)是可以平移的余弦曲线,但它的固有斜率太小,在限定α区间内,与x轴形不成交点。但交点是数理解析问题的关键。宝钢飞剪取R2-R1=30 mm,把固有斜率线性地放大了30倍,使其成为“陡峭”的近似直线。促使在α区间内,与x轴形成了须用的交点。该交点相关值的确定可令公式(4):(R2-R1)×cosα+Cj=0,并以x轴记数时,则有: (6) 宝钢飞剪取Δj(Δz)=0.4 mm,符合剪刃侧间隙的经验取值范围。那么Cj=2=3.6 mm代入公式(6)计算,则α=263.1079°(即图2Cj=2的Δz(α)曲线与X轴的交点C)。相关各值见表1。栏Ⅳ第2行Cj=2=3.6 mm的Δj=0是从基准D点起,连续调节工艺侧间隙大小的终点C。则该二零(交)点的侧间隙值C:[-0.4~ 0];D:[0~0.4]。定义[C,D]为板坯断裂闭区间。在该区间内,任意1点的侧间隙值中恒有与X轴相交1点的Δj=0。 无论C点或D点,在给定α全区内,表1栏Ⅳ两行任意一点的差,代入公式(5)计算 [Δz(α)+cj=2]-[Δz(α)+cj=1]≡0.4 mm 满足了理论和实践的要求。其几何意义如图2所示,取值范围在上下剪刃位移对应点的“距离”恒定的两条余弦曲线。剪刃侧间隙调整范围,cj=3.2~3.6 mm的连续表达形式,符合数学定理。 1.1[C,D]区间断裂点“考证”与分析 1.2剪切工艺侧间隙Δj的调节 工艺规程确定后,一台切头飞剪的剪刃工艺侧间隙Δj一般不再变动。上述取常数Cj=1=3.2 mm,实际是LRj中央1点p为下剪刃Rj的定位点。它只能轴(R1)向移动。Cj=2=3.6 mm实际是LRj中央1点p上剪刃Rj的位置。它可以定轴(R2)横向摆动,也可以轴向移动。Cj=3.2~3.6 mm连续调动的目的,主要是在装配、安装、更换刀片时实现Cj=1,Cj=2的准确位置,以保证二余弦函数曲线对应点剪切工艺侧间隙Δj≡0.4 mm。所以精度要求是双重的,除Δj大小外,还有对应点的位置精度。不过该位置精度与上下剪刃Rj的中心线重合精度要求是一致的。只要后者精度达到了,Δj也就满足了。 1.3滚筒式飞剪机能耗 现场看到的图2a切头断面畸形是R2≫R1所致,剪切厚度突破hmax=40 mm的历史记录,滚筒飞剪机剪切板坯厚度hmax≥60 mm时出现的。因为剪刃线速度差太大,造成剪切板坯断面连续“滑移”,剪刃一直处在侧间隙为-Δz的压入板坯过程中。直到逼近试验值时,设计者使用数学、力学方法进行平移侧间隙曲线,造成复杂应力,迫使板坯在预定位置断裂。结果还是压入滑移段占了全过程的93﹪以上,断裂段不足7﹪.(连杆式切头飞剪分别约为60﹪和40﹪。且无因线速度差造成的断面滑移。)做功能耗过大。尤其在剪切的初级阶段,剪刃压入板坯的面积由小增大,压强减小,阻力矩急剧增大,作用力的方向连续变化等整个过程处在动态中,能量损失严重。此外图2a板坯宽度为Bs的畸形断面“嘴”是否有造成二次低温硬带头的可能,应与连杆式切头飞剪进行相应的测定比较。 图2所示的间隙曲线等,没有考虑LRj左、右旋问题。图1所示的α01角是飞剪区段传动辊道标高下降量的基准。 2鞍钢滚筒式切头飞剪机R1=R2型剪切工艺过程分析 这种型式飞剪是由国内设计,与国外合作制造成功的。剪切工艺示意图与图1基本相同。不过一个滚筒上两把剪刀[5]的相位差为90°,与图1所示的不同。文献[6]称[文献5]滚筒式切头飞剪为“同周速飞剪”,R1=R2=504 mm。其余参数[5]Hg=1 000 mm,剪刃最大重合度为8 mm,热板坯hmax×Bs=40 mm×1 550 mm,板坯圆弧头半径Rj=19 330 mm,剪刃平移侧间隙调节范围Cj=0.6~0.9 mm,起动工作制。 由于R1=R2,公式(3)不能直接用于该飞剪的计算。在给定α区间内,按滚筒飞剪机固有余弦函数曲线斜率进行计算。令A=1(mm),则 Δz=A·cosα (7) 将该型飞剪的相关数值代入公式(1)、(2)、(7)、(4)、(5)进行计算,结果列见表2,据此做出图3。分别将平移值Cj=1=0.6 mm和Cj=2=0.9 mm代入(4)式计算,将两次的结果按公式(5)求差值,任意对应一点的Δj≡0.3 mm(见表2第Ⅳ栏)。 该型飞剪确定定位点的自由度大,可以选定下剪刃或上剪刃只做轴向移动,另一剪刃做双向调动。这种型飞剪国内多处使用。 图3 鞍钢滚筒式切头飞剪机R 1=R 2 Fig.3 Rotary cutting head flying shear of Ansteel 给定剪刃半径R转角α或-α/(°)待切入板坯高度hj(或剪刃重叠量-h,开口度h)/mm剪刃自然位移侧间隙ΔZ/mm剪刃工艺侧间隙公式Δj=ΔZ(α)+CjCj=1=0.6mmCj=2=0.9mmⅠⅡⅢⅣ25241.33503157-0.3090169940.2909830060.590983006252.2472140-0.3049106750.2950893250.59508932525336.04480599-0.2923717050.3076282950.607628295……………2621.809786708-0.1391731010.4608268990.760826899262.7766310-0.1257378730.4742621270.774262127263-0.486520854-0.1218693430.4781306570.778130657……………270-800.60.9……………277-0.4865208540.1218693430.7218693431.0218693432781.8097867080.1391731010.7391731011.039173101……………28736.044805990.2923717050.8923717051.192371705287.75279400.3049106750.9049106751.20491067528841.335031570.3090169940.9090169941.209016994 武钢热连扎厂切头飞剪机也是从日本引进,属于R1=R2型。但曾按R1>R2型做了分析,得出了可行结论。 3结论 (1)分析了引进的滚筒式热板坯切头飞剪机设计理论,对上下剪刃任意点的剪切板坯高度hj=hj(α)和自然位移剪刃侧间隙Δz=Δz(α)进行了计算; (2)得出了剪切工艺过程剪刃侧间隙恒定的结论; (3)上下剪刃位移间隙是连续可调的。 参考文献: [1]冶金工业部武汉钢铁设计研究院.板带车间机械设备设计(下册)[M].北京:中国冶金工业出版社, 1984: 210-219. [2]В.С.Терентбев,М.Б.Чалюк.常森等译。薄板车间精整设备[M].北京:中国工业出版社, 1964: 196-207. [3]А.И.целиков,В.Всмирнов.哈尔滨工业大学工艺教研室译轧钢设备[M].北京:中国工业出版社, 1962: 245-251. [4]邹家祥,施东成. 轧钢机械理论与结构设计(下册)[M].北京:冶金工业出版社, 1993: 150-155. [5]赵华国. 滚筒式切头飞剪结构介绍[J].一重技术 2003(1). [6]汪建春. 刘旺异周速双滚筒切头飞剪结构特点及分析[J].重型机械 2007(4): 35-37. [7]柳冉,蒋继中,赵建刚,等.滚筒机构螺旋剪刃飞剪机静态剪切力计算公式探讨[J].重型机械,2001(3).