基于子带分解的MSR雾天图像增强算法
2016-01-08舒婷,刘耀峰,邓波等
基于子带分解的MSR雾天图像增强算法*

舒婷,刘耀峰,邓波,谭亚鹏,陈炳权
(吉首大学物理与机电工程学院,湖南 吉首 416000)
摘要:提出了一种基于子带分解的MSR的图像增强算法(Subband-Decomposed Multiscale Retinex,简称SDMSR).先利用改进后的MSR算法对雾天图像进行处理,之后由子带分解的方法对雾天图像的不同子带分解输出进行增益,最后采用图像融合技术得到清晰的增强图像.并借助均值、标准差、熵、均方误差(MSE)和峰值信噪比(PSNR)对文中算法的仿真结果进行了定量评价,仿真与评价结果表明,该算法能够提高雾天图像的对比度,保留了原图像中有用的信息,图像的失真程度小,图像的清晰度也得到了提高.
关键词:子带分解;Retinex理论;SDMSR算法;均值;标准差;MSE;PSNR
文章编号:1007-2985(2015)01-0040-06
中图分类号:TP391.411文献标志码:A
DOI:10.3969/j.issn.1007-2985.2015.01.010
收稿日期:*2014-06-16
基金项目:湖南省教育厅科学研究资助项目(14C0920)
作者简介:舒婷(1989—),女,湖南娄底人,吉首大学物理与机电工程学院无线电物理硕士研究生,主要从事信号处理与模式识别研究.
通信作者:陈炳权(1972-),男,湖南桃源人,吉首大学物理与机电工程学院副教授,工学博士,硕导,主要从事信号处理与智能控制研究.

近年来,世界各地遭受到不同程度的雾霾天气影响,雾霾天气不仅对人体健康危害大,而且对户外视频监控系统的图像采集带来了挑战.研究雾天环境下的图像增强算法具有一定的现实意义.在雾霾环境下采集的视频图像存在能见度和对比度低以及颜色失真等问题.许多学者为解决该问题提出了一系列雾天图像增强算法.20世纪60年代,Land首次提出了Retinex理论,该理论将图像分解为反射图像和亮度图像,去除光照的影响,从而得到最终的反射图像.在该理论的基础上,Jobson、Rahman和Woodell等[2-6]提出了一系列算法,对经典Retinex算法的卷积函数进行一系列地改进,得到单尺度Retinex(Single-Scale Retinex,SSR)算法,利用不同尺度下的SSR算法进行加权平均得到多尺度Retinex(Multi-Scale Retinex,MSR)算法,在MSR算法中引入颜色恢复功能得到带色彩恢复因子的多尺度Retinex(Multi-Scale Retinex with Color Restoration,MSRCR)算法.该3种算法的共性:反射图像代表图像的细节部分,也就是图像的本质特性;尺度的大小可以调节,其图像分辨率会因尺度的变化而变化,尺度越大图像轮廓越清晰,尺度越小图像细节越清晰.然而,上述算法只考虑图像阴暗处的增强,而没有对图像明亮处进行增强,明亮部分处常常出现光晕现象,文献[8-10]对图像阴暗和明亮部分同时进行增强,提出了由混合灰度转换函数取代Retinex算法中的灰度转换函数,并引入子带分解策略,保持了各子带间的独立性.
鉴于上述分析,笔者提出了一种基于子带分解的多尺度Retinex算法(SDMSR算法).在MSR算法基础上,利用混合灰度转换函数取代原有Retinex算法中的灰度转换函数,并利用子带分解的特征来保持各个频带之间的独立性.文中给出了该算法的流程图,并运用均值、标准差、熵、均方误差(MSE)和峰值信噪比(PSNR)[11]等5项评价指标对仿真结果进行了定量分析,研究结果表明了本文算法对雾天图像增强的正确性和有效性.
1Retinex理论
Retinex理论解释了视觉系统是如何对视觉信息进行处理并保持视觉颜色恒常,阐述了同一个物体在不同的环境下颜色是恒定的.其基本原理就是将原图像分为反射和亮度图像,并降低亮度图像对反射图像的影响而实现图像增强,其数学模型为
S(x,y)=R(x,y)×I(x,y),
(1)
其中:S(x,y)表示原待增强图像;R(x,y)表示反射图像;I(x,y)表示亮度图像.
对(1)式两边同时取对数可得到
logS(x,y)=logR(x,y)+logI(x,y),
变形之后,则

(2)
在Retinex理论和单尺度Retinex(SSR)算法的基础上,多尺度Retinex算法表示为

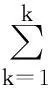

其中:高斯函数的标准差σk即为第k个尺度参数;K为一个常数;Fk(x,y)满足∬F(x,y)dxdy=1.
2基于子带分解的MSR算法
在MSR算法中引入混合灰度转换函数,在不同的尺度参数条件下,充分利用子带分解特性,分别对雾天图像的3个颜色通道进行处理,由此得到不同的输出结果,最后利用文献[12]的图像像素灰度值加权融合算法得到高质量的清晰图像.文中提出的SDMSR算法的数学模型为
Rk(x,y)=h_log(S(x,y))-h_log(Fk(x,y)*S(x,y)).
(3)
其中:Rk(x,y)表示对应不同尺度下的Retinex输出图像;h_log(S(x,y))表示混合灰度转换函数,且
h_log(S(x,y))=ω·S+(x,y)+(1-ω)·S-(x,y),
S+(x,y)=log(S(x,y)+1),
S-(x,y)=logD-log(D-S(x,y)).
其中D表示图像动态范围,8位图像的动态范围为0~256.

(4)

(5)
其中:

(6)
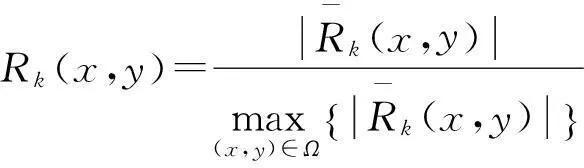
(7)
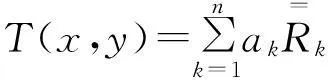
(8)
其中:T(x,y)为最终输出图像;ak为加权函数.

3本文算法流程
本文算法流程如下:
(1)输入雾天图像S(x,y),并将其分解为RGB这3幅灰度图像,即Sr(x,y)、Sb(x,y)和Sg(x,y),并将对应图像中像素点灰度值数据类型转为双精度double型;
(2)对雾天图像S(x,y)进行对数域处理,并引入混合灰度转换函数代替原有的灰度变换函数,得到不同尺度下对应的Retinex输出图像Rk(x,y);

(5)利用图像像素灰度值加权融合算法(即(8)式)进一步处理,得到高质量的最终清晰图像T(x,y).
4仿真结果及分析
4.1 仿真结果
本文仿真实验在Windows7系统操作下(2.10GHzIntel(R)Core(TM)i3-2310MCPU),运用Matlab2010a完成.实验选取2组大小为375×264的图像,雾天图像为实际场景拍摄,第1组为薄雾图像,第2组为浓雾图像.对2组雾天图像分别使用多尺度Retinex算法、SDMSR算法进行增强,第1,2组实验结果及其对应的直方图如图1至4所示.

图1 薄雾图像采用3种不同算法的效果
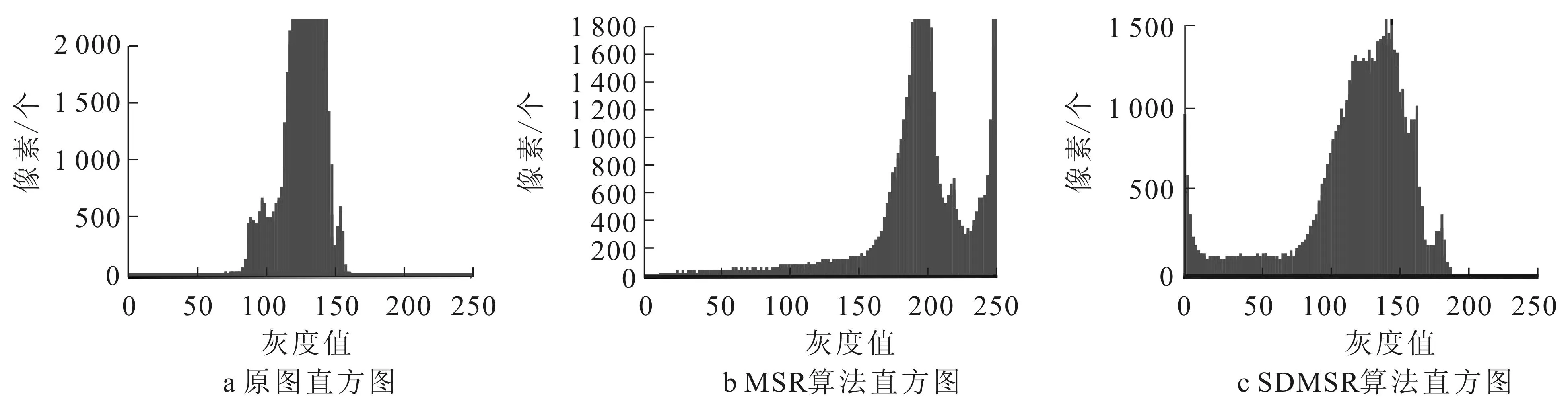
图2 图1图像所对应的直方图

图3 浓雾图像采用不同增强算法的效果

图4 浓雾图像增强后所对应的直方图
第1组薄雾图像仿真结果表明,经MSR算法处理后的图像亮度提升比较明显,但图像下半部分的建筑物存在一定程度的过度增强,导致图像失真,而经SDMSR算法处理后的图像亮度适中,颜色恢复较好,建筑物清晰,且有层次感,整体视觉效果也得到了改善,且提升了图像的亮度动态范围.第2组浓雾图像仿真结果表明,经过MSR算法处理后的图像对比度得到较大幅度提升,但亮度也得到提升,而经过SDMSR算法处理后的图像对比度得到较大幅度提升,但亮度反而降低,且图像存在失真现象.
4.2 仿真结果分析
文中采用均值(表示图像的均衡亮度值,图像均值越大,图像的均衡亮度越高)、标准差(表示图像的对比度,图像标准差越大,图像的对比度就越大)、熵(表示图像的信息量大小,熵越大,图像所含的信息量就越多)、均方误差MSE(表示图像失真的程度,MSE值越小表示图像失真程度越小)和峰值信噪比PSNR[11](表示最大信号量与噪声强度的比值,PSNR值越大表示图像越清晰)等5个参数,作为雾天图像处理效果评价指标.对于大小为M×N的图像,均值μ、标准差σ、熵H(p)、均方误差MSE和峰值信噪比PSNR的定义分别如下:

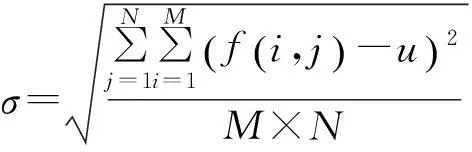


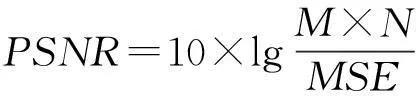
其中:f(i,j)代表坐标为(i,j)的像素值;f′(i,j)代表降质图像相应坐标点的像素值;L表示图像的灰度级数,其默认值为256;p(m)表示图像中像素点灰度值为m的概率分布.文中的2组图像增强的客观数据分别如表1所示.
从表1可以看出:第1组薄雾图像经SDMSR算法处理后,且熵比原图像高出了1.065 3,比经MSR算法处理后图像的熵高出0.368 6;经SDMSR算法处理后图像比经MSR算法处理后图像的均方误差降低了5464;经SDMSR算法处理后的图像比经MSR算法处理后图像的峰值信噪比高了18.915 4.第2组经SDMSR算法处理后图像的熵比原图像高出了0.137 9,比经MSR算法处理后图像的熵高出了0.880 5;经SDMSR算法处理后图像比经MSR算法处理后图像的均方误差高出了166.4;经SDMSR算法处理后图像比经MSR算法处理后图像的峰值信噪比降低了0.686 3.仿真实验表明:经SDMSR算法处理后的图像信息量更多,图像细节更明显,视觉效果更好,较原雾天图像,其对比度得到了较大提高.
5结语
在Retinex理论的基础上,提出了基于子带分解的MSR雾天图像增强算法,利用该算法处理后的雾天图像信息量PSNR较MSR得到了较大提升,图像细节明显,视觉效果更好,对比度得到提高,但还存在一些工作有待完善.在图像融合过程中,能否自适应地选择加权参数从而得到最佳输出图像,将有待进一步研究.
参考文献:
[1]LANDE.TheRetinex.AmSci,1964,52(2):247-264.
[2]RAHMANZ,JOBSONDJ,WOODELLGA.Multi-ScaleRetinexforColorImageEnhancement//ImageProcessing,1996.Proceedings.,InternationalConferenceon.IEEE,1996,3:1 003-1 006.
[3]JOBSONDJ,RAHMANZ,WOODELLGA.PropertiesandPerformanceofaCenter/surroundRetinex.ImageProcessing,IEEETransactionson,1997,6(3):451-462.
[4]MOOREA,ALLMANJ,GOODMANRM.AReal-TimeNeuralSystemforColorConstancy.NeuralNetworks,IEEETransactionson,1991,2(2):237-247.
[5]JOBSONDJ,RAHMANZ,WOODELLGA.AMulti-ScaleRetinexforBridgingtheBetweenColorImagesandtheHumanObservationofScenes.IeeeTransactionsonImageProcessingforAutomaticImageEnhancement.JournalofElectronicImaging,2004,13(1):100-110.
[6]RAHMANZ.InvestigatingtheRelationshipBetweenImageEnhancementandImageCompressionintheContextOfTheMulti-ScaleRetinex.JournalofVisualCommunicationandImageRepresentation,2011,22(3):237-250.
[7]方志军,等.基于子带加权融合的多尺度Retinex图像增强算法.山东大学学报:理学版,2013(48).
[8]JANGJH,CHOIB,KIMSD,etal.Sub-BandDecomposedMultiscaleRetinexwithSpaceVaryingGain//ImageProcessing,2008.ICIP2008.15thIEEEInternationalConferenceon.IEEE,2008:3 168-3 171.
[9]JANGJH,KIMSD,RAJB.EnhancementofOpticalRemoteSensingImagesbySubband-DecomposedMultiscaleRetinexwithHybridIntensityTransferFunction.GeoscienceandRemoteSensingLetters,IEEE,2011,8(5):983-987.
[10]JANGJH,BAEY,RAJB.Contrast-EnhancedFusionofMultisensoryImagesUsingSubband-DecomposedMultiscaleRetinex.ImageProcessing,IEEETransactionson,2012,21(8):3479-3490.
[11]BJONTEGAARDG.documentVCEG-M33:CalculationofAveragePSNRDifferencesBetweenRD-Curves//ITU-TVCEGMeeting,Austin,Texas,USA,Tech.Rep.2001.
[12] 赵小川.现代数字图像处理技术提高及应用案例的详解(MATLAB版).北京:北京航空航天大学出版社,2011:112-132.
Multi-Scale Retinex Algorithm for the Foggy Image Enhancement
Based on Sub-Band Decomposition
SHU Ting,LIU yaofeng,DENG Bo,TAN Yapeng,CHEN Bingquan
(College of Physics and Mechanical & Electrical Engineering,Jishou University,Jishou 416000,Hunan China)
Abstract:A kind of Multi-Scale Retinex (MSR) algorithm based on sub-band decomposition for image enhancement was proposed.First,the improved MSR algorithm was used to deal with the foggy image.Then,the gain of the different foggy image was obtained by the sub-band decomposition method.After that,the clear and enhanced image was obtained by the image fusion technology.At the same time,the simulation results of the algorithm was analyzed by using the mean value,standard deviation,entropy and mean square error (MSE) and peak signal-to-noise ratio (PSNR).The simulation and evaluation results show that the contrast of image is increased,the useful information of the original image is retained,the degree of distortion is small,and the clarity of the image can be improved.
Key words:sub-band decomposition;Retinex algorithm;sub-band decomposition multi-scale retinex (SDMSR);mean value;standard deviation;mean squared error(MSE);peak signal-to-noise ratio(PSNR)

