关于正整数的四次方部分数列的和
2016-01-08高丽,赵喜燕
关于正整数的四次方部分数列的和*

高丽,赵喜燕
(延安大学数学与计算机科学学院,陕西延安 716000)
摘要:利用初等和解析的方法研究了Smarandache提出的数列的求和问题,即研究正整数的四次方部分数列的和,得出2个有趣的求和公式.
关键词:Smarandache问题;四次方部分数列;求和公式
文章编号:1007-2985(2015)01-0005-02
中图分类号:O156.4文献标志码:A
DOI:10.3969/j.issn.1007-2985.2015.01.002
收稿日期:*2014-06-20
基金项目:国家自然科学基金资助项目(11471007);陕西省科学技术研究发展计划项目(2013JQ1019);延安大学高水平大学建设项目(2012SXTS07);延安大学2014年科研计划项目
作者简介:高丽(1966—),女,陕西绥德人,延安大学数学与计算机科学学院教授,硕士生导师,主要从事数论研究.

Smarandache问题的提出受到了许多数学爱好者的关注,许多专家和学者对Smarandache问题进行了深入研究,并得到了很多重大成果[4-7].
文献中的第41个问题,是有关数列a(n)和b(n)的性质.张少杰研究了a(n)和b(n)的渐近性质.郭金保等研究了正整数的立方数列求和,得出如下结论:
若a(n)表示不超过n的最大立方数,则对任意正整数n,有


若b(n)表示不小于n的最小立方数,则对任意正整数n,有
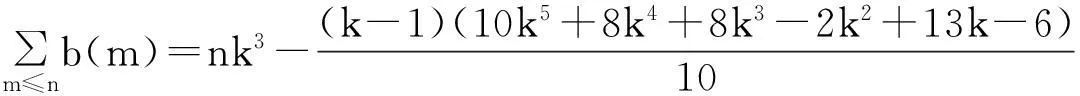

国债又被称作国家公债,即为国家中央政府以自身信用为基础,按照一般债券的发行原则,面向社会筹集资本而形成一种债券债务关系。国债是政府债券的一种,以政府税收作为到期偿还持有者本息的保证,也是拥有最高信用度、最具公信力、最安全的投资工具。
笔者将利用初等和解析的方法讨论正整数的四次方数列的求和问题.
对任意的正整数n,设a(n)表示不超过n的最大四次方部分,b(n)表示不小于n的最小四次方部分,例如:
a(1)=1,a(2)=1,a(3)=1,a(4)=1,…,a(16)=16,…;
b(1)=1,b(2)=16,b(3)=16,b(4)=16,…,b(16)=16,b(17)=81,….
那么,有如下结论成立:
定理1对任意的正整数n,设k是一固定的正整数,且满足k4≤n<(k+1)4,则a(n)=k4,

证明对任意的正整数n,设k是一固定的正整数,且满足k4≤n<(k+1)4,由a(n)的定义可知a(n)=k4(k4≤n<(k+1)4),则有
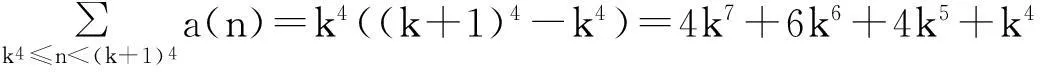
(1)
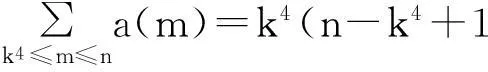
(2)
由(1),(2)式可知
4(1+27+…+(k-1)7)+6(1+26+…+(k-1)6)+
4(1+25+…+(k-1)5)+(1+24+…+(k-1)4)+
k4(n-k4+1).
(3)
由文献可得:
5(k-1)3-5(k-1)2-2k+4],
(4)
6(k-1)3-6(k-1)2-k+2],
(5)

(6)

(7)
所以由(3)—(7)式得

证毕.
定理2对任意的正整数n,设k是一固定的正整数,且满足(k-1)4 证明对任意的正整数n,设k是一固定的正整数,且满足(k-1)4 (8) (9) 由(8),(9)式可知 4(1+27+…+(k-1)7)-6(1+26+…+(k-1)6)+ 4(1+25+…+(k-1)5)- (1+24+…+ (k-1)4)+k4(n-(k-1)4). (10) 所以由(10),(4)—(7)式得 证毕. 参考文献: [1]APOSTOL T M.Introduction to Analytic Number Theory.New York:Springer-Verlag,1976. [2]SMARANDACHE F.Sequences of Number Involving in Unsolved Problem.USA:High American Press,2006. [3]SMARANDACHE F.Only Problems,Not Solutions .Chicago:Xiquan Publishing House,1993. [4]ZHANG Wenpeng.Research on Smarandache Problems in Number Theory(Collected Papers).USA:High American Press,2004. [5]ZHANG Wenpeng.Research on Smarandache Problems in Number Theory(Vol.Ⅱ).USA:High American Press,2005. [6]YI Yuan,KANG Xiaoyu.Research on Smarandache Problems.USA:High American Press,2006. [7]LIU Huaning,GAO Jing.Research on Smarandache Problems.USA:High American Press,2011. [8]张少杰.关于正整数的四次方部分数列.价值工程,2011,29:221-222. [9]郭金宝,郭永平.正整数的立方数数列的求和.延安大学学报:自然科学版,2005,24(4):3-4. Part Summation of 4th Sequences of Positive Integer GAO Li,ZHAO Xiyan (School of Mathematics and Computer Science,Yan’an University,Yan’an 716000,Shaanxi China) Abstract:We use the elementary methods and analytic methods to study the part summation of 4th sequences of positive integer,and give two interesting summation formula. Key words:Smarandache problem;4thsequences;summation formula (责任编辑向阳洁)





