基于Copula函数的航班延误相关性分析*
2016-01-08邱树萍吴薇薇侯美丽
邱树萍 吴薇薇 侯美丽
(南京航空航天大学民航学院 南京 210016)
基于Copula函数的航班延误相关性分析*
邱树萍吴薇薇侯美丽
(南京航空航天大学民航学院南京210016)
摘要:不同因素引起的航班延误产生的波及影响是不同的.运用Copula理论研究了由空中管制原因导致的初始延误引发的连续航班延误之间的相关性,并进一步分析了初始延误对次航班的波及效应.研究发现两航班延误时间都较长的组合数对出现的频率较高;初始延误对次航班的波及影响跟初始延误时间长短有关.随着初始延误时间的增长,对次航班波及影响表现为吸收的可能性增加,延误传递和增强的可能性下降.
关键词:航空运输;相关性;Copula理论;航班延误;波及效应;尾部相关
邱树萍(1989- ):女,硕士生,主要研究领域为交通运输系统优化
0引言
由于航班之间存在飞行器、机组及服务人员等资源共享,同时航空公司在安排运行计划时,考虑到运行成本最小化和资源利用最大化目标,一旦某个航班遭受延误很大程度上会影响后续航班的正常运行,即形成延误波及效应.国内外一些学者运用多种不同的方法进行了研究.如文献[1]通过构造贝叶斯网络模型探讨了国内某枢纽机场进港航班延误和航班取消对离港航班延误的影响.文献[2]提出了用构造航班延误波及树的方法,清晰的展现了根节点延误通过机组和飞机资源在网络中传播的过程.文献[3]提出了延误加法器的概念用于评估延误的累计,引入了延误累积(delay multiplier,DM)指标评估初始延误造成的总延误影响.这些文献针对航班延误对后续航班的波及影响运用了不同的方法,主要是从飞行资源、进离港延误角度进行研究,但都未涉及对初始延误引发的连续航班延误之间的相关性进行分析.文献[4]研究了边缘分布均为非正态分布的轮挡延误和登机门到达延误之间的相关性,采用了在金融风险建模、经济学、计量经济学中常用的一种方法——Copula函数.Copula函数是一种灵活稳健的相关性分析工具,尤其体现在研究随机变量间的相关关系上.如文献[5]引入Copula函数来代替传统方法估计VaR使得度量的相关性不再局限于线性相关性.文献[6]运用混合Copula函数对上海、深圳股票市场进行了相关分析研究,其结果体现了混合Copula函数的灵活性.
本文利用Copula函数建立2连续航班延误的联合分布,借助建立的联合分布函数计算2连续航班延误分别落在不同区间的条件概率,由此进一步分析由空中管制原因导致的初始延误对后续航班的波及影响——吸收、传递或增强.
1研究方法
1.1Copula理论
Copula的研究最早源于Sklar,Copula一词原意是交换、连接的意思.Nelse对Copula函数做了严格的定义,Copula函数是把随机变量ξ1,ξ2,…,ξn的联合分布函数F(x1,x2,…,xn)与各自的边缘分布函数Fξ1(x1),Fξ2(x2),…,Fξn(xn)相连接的连接函数,即函数C(u1,u2,…,un),使
(1)
与传统的线性相关系数相比,Copula模型不限制边缘分布的选择,且当对变量作单调增变换时,由Copula函数导出的一致性和相关测度的值不会改变,因此使用Copula函数进行建模将变得更加灵活.常用的Copula函数有二元正态Copula函数、二元t-Copula函数、Gumbel Copula函数、Clayton Copula函数、Frank Copula函数.它们的密度函数都有各自的分布特征能刻画不同的随机变量之间的相关关系.
1.2Kendall秩相关系数τ
在统计学中,Kendall相关系数是一个基于非参数检验方法得到的相关性统计量.设(x1,y1),(x2,y2)为独立同分布的向量,则Kendall相关系数为
(2)
式中:P[(x1-x2)(y1-y2)>0]为x与y的变化一致的概率,因此τ反映了x与y变化一致与否的程度.本文主要应用Kendall的τ与Copula函数关系进行相关参数计算,Kendall的τ与Copula函数之间的关系为[7]
(3)
2实例分析
2.1确定边缘分布函数
本文采用的研究数据来源于国内某航空公司提供的若干个月的航班延误数据,包含了736对基于航班串的由空中管制原因导致的初始延误引发的连续航班.航班延误数据均来自到达延误,如图1所示航班A和航班B由同架飞机执行,航班A到达机场b时延误(延误由空中管制原因导致),航班B受航班A波及影响到达机场c时延误,需要说明的是航班A不一定是飞机执行的第一个航班,而是航班串中首个遭受延误的航班.将2航班延误作为随机变量,采用正态分布、对数正态分布、威布尔分布、伽马分布这4种连续变量概率分布函数对2个随机变量的服从的边缘分布函数进行分析.运用极大似然估计对连续概率分布函数进行参数估计,并通过Cramer-von Mises检验方法对2连续航班延误随机变量进行拟合优度检验,以确定最优概率分布函数.根据拟合优度检验结果选择样本A和样本B最优边缘分布均为对数正态分布,相应参数和检验统计量见表1.

图1 航班执行示意图
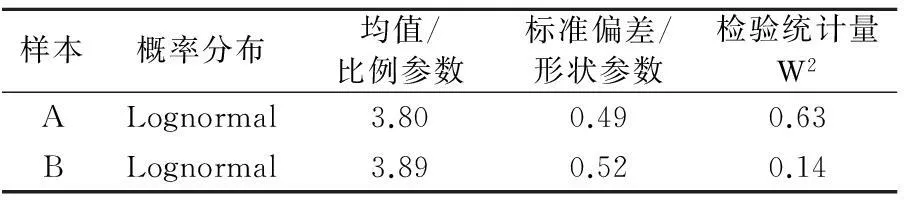
样本概率分布均值/比例参数标准偏差/形状参数检验统计量W2ALognormal3.800.490.63BLognormal3.890.520.14
2.2Copula函数的参数估计及拟合优度评价
利用SAS软件计算两个变量的秩相关系数τ=0.252 9.通过秩相关系数τ与Copula函数的关系式计算出各Copula函数的参数θ,然后计算五种Copula函数与经验Copula函数的平方欧式距离d2作为检验其拟合优度的标准,结果见表2.根据拟合优度评价指标,选择d2值最小的为最优拟合Copula函数.结果显示Gumbel Copula函数为最优拟合Copula函数.

表2 5种Copula函数的参数及拟合评价指标
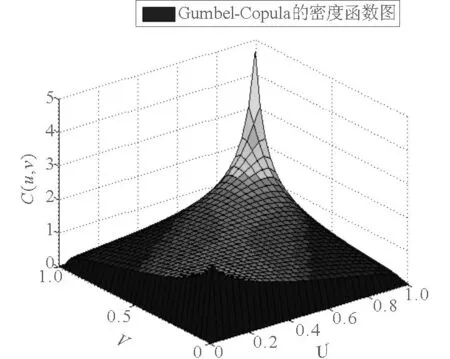
图2 Gumbel Copula密度函数图
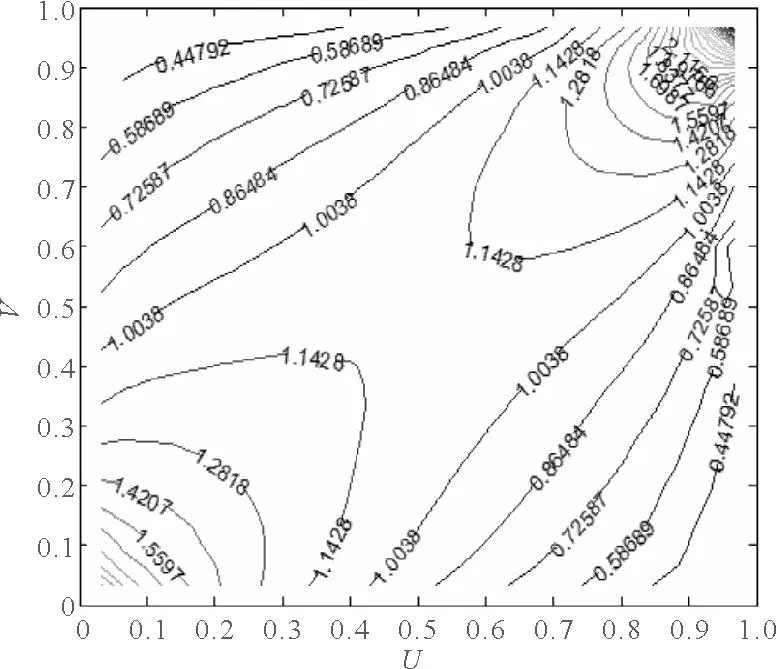
图3 Gumbel Copula等高线图
图2和图3分别为为Gumbel Copula密度函数图和等高线图,二元Gumbel Copula的密度函数具有不对称的尾部,对变量在分布的上尾的变化较敏感,能很好的捕捉到上尾相关的变化.从图2和图3中可以看出,2连续航班延误之间存在上尾部相关性,即2航班延误时间都较长的组合数对出现的频率较高.通过尾部相关系数可以分析极值事件发生的频率.尾部相关性是一种极值相关性的度量,即当一个观测变量的出现值为极值时,另一个也出现极值的概率.Gumbel Copula函数上尾部相关系数与参数θ的关系为λup=2-21/θ,由θ=1.321 7得上尾相关系数λup=0.31,下尾部相关系数为0说明分布在尾部变量间是渐近独立的.
2.3条件概率分布
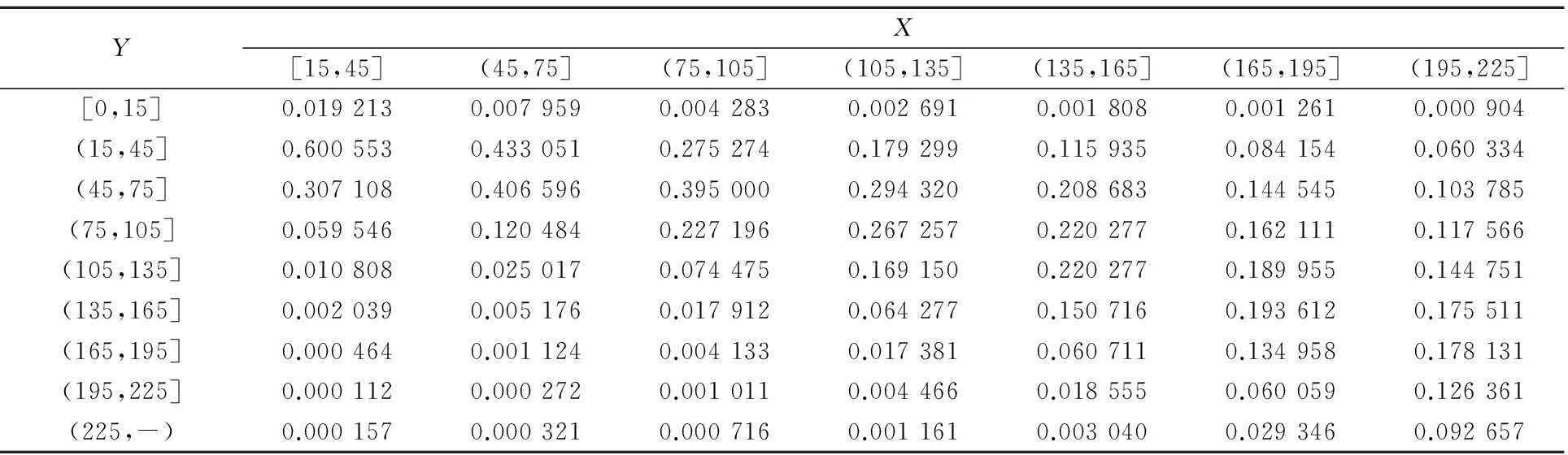
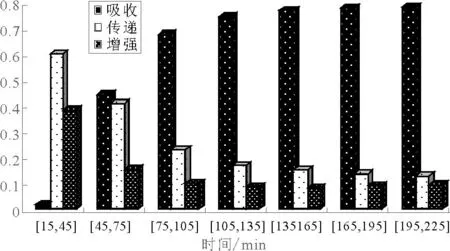
计算条件概率P(y1 从表3中纵向比较来看,当A航班延误落在某个区间时,B航班延误落在比A航班延误小的区间的概率要大于落在比A航班延误大的区间的概率.由此说明由空中管制原因导致的初始延误对次航班延误的波及影响表现为吸收的可能性要大.从横向与纵向的对称位置上进行比较,如P(45 表3 A航班延误与B航班延误条件概率 图4 为初始延误对次航班波及影响表现为吸收、传递或增强所占比例的柱状图分析.由图4可见,初始延误对次航班波及影响表现为吸收的可能性成增长趋势,初始延误时间大于105 min时这种增长趋于平稳;对次航班波及影响表现为传递和增强的可能性均成下降趋势,这种下降趋势最终也趋于平稳.当初始延误时间大于75 min时对次航班的波及影响主要表现为吸收,所占比例在70%左右;初始延误时间在15 min和45 min之间时延误60%的可能性传递,接近40%的可能性增强. 图4 初始延误对次航班波及影响 通过以上分析发现由空中管制原因导致的初始延误引发的连续航班延误之间的相依关系表现为上尾高下尾低,上尾相关系数为0.31;由空中管制原因导致的初始延误对次航班波及影响跟初始延误时间的长短有关.初始延误时间长短不同次航班表现为吸收、传递或增强的可能性不同;随着初始延误时间的增长,对次航班波及影响表现为吸收的可能性增加,延误传递和增强的可能性下降. 3结束语 航班计划执行过程中随时都有可能遭受到随机因素的扰动影响,航班计划安排的越紧凑延误在航线网络中造成的波及影响范围越大.本文利用Copula函数构建了由空中管制造成的初始延误和受此航班延误波及的次航班延误之间的联合分布,分析了两连续航班延误之间的相依关系和延误时间分别落在不同区间上的条件概率.结果表明航班延误沿飞机路线向下游航班传播的概率大小跟初始延误的时间长短有很大关系. Copula函数是研究随机变量间的相关性分析工具,对小样本数据的拟合效果比较好.本文基于Copula函数对由空中管制原因导致的初始延误及受波及的次航班延误影响的非线性相关关系充分揭示出来,并充分利用Gumbel Copula分布函数特征分析了因空中管制原因导致的初始延误时间的不同而对次航班带来不同的航班延误波及影响.研究存在的不足之处在于只考虑了空中管制对后续航班的影响,没有考虑其它延误因素的影响作用,今后研究重点将放在多因素对航班延误波及的影响. 参 考 文 献 [1]刘玉洁,何丕廉,刘春波,等.基于贝叶斯网络的航班延误及研究[J].计算机工程与应用,2008,44(17):242-245. [2]AHMADBEYGI S,COHN A,GUAN Y,et al.Analysis of the potential for delay propagation in passenger airline networks [J]. Journal of Air Transport Management,2008,14(5): 221-236. [3]BEATTY R, HSU R, BERRY L,et al. Preliminary evaluation of flight delay propagation through an airline schedule[J].Air Traffic Quarterly,1999(7):259-270. [4]DIANA T.Improving schedule reliability based on copulas:an application to five of the most congested US airports[J].Journal of Air Transport Management, 2011(17):284-287. [5]朱世武.基于Copula的VsR度量与事后检验[J].数理统计与管理,2007,26(6):984-991. [6]李秀敏,史道济.沪深股市相关结构分析研究[J].数理统计与管理,2006,25(6): 729-736. [7]HUARD D,EVIN G,FAVRE A C.Bayesian copula selection[J].Journal of Computational Statistics & Data Analysis,2006,51:809-822. 中图法分类号:[U8] doi:10.3963/j.issn.2095-3844.2015.01.027 收稿日期:2014-11-10 Correlation Analysis of Flight Delay Based on Copula Function QIU ShupingWU WeiweiHOU Meili (SchoolofCivilAviation,NanjingUniversityof AeronauticsandAstronautics,Nanjing210016,China) Abstract:Different flight delays caused by different factors will produce different results and propagations. Copula theory is introduced to study correlation between the sequence flight delays which caused by the initial delay for air traffic control and further analysis of propagation effects on following flight caused by initial delay flight is presented. It is found that the appearance frequency of assorted pairs is higher, and the assorted pairs belong to two flights delay with longer time; The initial delay propagation effects on the following flight is related to the time of initial delay. Results demonstrate that with the increase of initial delay time, the possibility of absorption of following flight in propagation effects is increased and the possibility of propagation and enhancement of delay is reduced. Key words:air transportation;correlation;Copula theory;flight delays;propagation effects;tail dependence *国家自然科学基金项目(批准号:71201081;71171111)、中央高校基本科研业务费专项科研项目(批准号:NO.NC2012005)资助