基于Mixed-Logit的半补偿型方式划分模型研究*

肖　林　卫　翀　陈小鸿　单肖年

(同济大学交通运输工程学院1)　上海　201804)　(同济大学道路与交通工程教育部重点实验室2)　上海　201804)

(北京交通大学交通运输学院3)　北京　100044)　(首都世界城市顺畅交通协同创新中心4)　北京　100124)

基于Mixed-Logit的半补偿型方式划分模型研究*

肖林1，2)卫翀3,4)陈小鸿1，2)单肖年1，2)

(同济大学交通运输工程学院1)上海201804)(同济大学道路与交通工程教育部重点实验室2)上海201804)

(北京交通大学交通运输学院3)北京100044)(首都世界城市顺畅交通协同创新中心4)北京100124)

摘要：引入阈值的概念，建立基于Mixed-Logit模型的半补偿型方式划分模型，将选择过程划分为2个阶段，并在第二阶段采用Mixed-Logit模型，克服IIA特性和喜好随机性限制两大缺陷，最终达到更好地描述出行方式选择行为的目的.基于SP调查获取的样本数据，采用马尔科夫链蒙特卡洛算法结合数据扩张技术的方法对模型参数进行标定，利用命中率法对模型预测结果进行检验，并与MNL模型进行对比，验证了该模型应用于交通方式划分的可行性及优越性.

关键词：方式划分；Mixed-Logit模型；半补偿型模型；阈值；SP调查

肖林(1991- )：男，硕士生，主要研究领域为交通运输规划与管理

0引言

目前，非集计模型已成为分析研究出行者方式选择行为的主要研究手段，并得到了广泛研究与应用.但以Logit为代表的非集计模型同样存在一定缺陷.受到IIA特性(independenceofirrelevantalternatives)，和喜好随机性限制(limitationofrandomtastevariation)，对模型预测精度影响较大[1].

Swait，Bhat，V.Cantillo等[2-4]研究表明，出行者在进行选择时对交通方式重要的属性值存在阈值要求，如当某公交车的出行时间超过一定时间后，则不再考虑乘坐公交车，此时公交车被选择的概率存在一个“突变”.基于补偿型效用函数的Logit模型以及NL模型显然无法很好地描述这种现象.因此，对非集计模型进行改进，减少甚至避免以上缺陷对预测结果的影响，更为科学合理地描述出行者的出行方式选择行为是本文的研究重点.

1模型建立与推导

1.1随机效用理论

随机效用理论(randomutilitytheory)将消费者行为理论中的最大效用假设与概率论相结合，用以解决多方案选择问题[5].基于随机效用理论并假设其随机效用项服从Gumbul分布进而推导出Logit模型的选择概率公式如下.

(1)

式中：Uni，Vni,εni分别为出行者n对选择肢i的效用、固定效用和随机效用；Pni为出行者n选择i的概率.

2.2出行方式选择决策流程——2阶段选择

前文已提到，当选择肢某属性值达到阈值时，出行者的选择行为规律将发生“突变”.Manski提出引入阈值的概念，将每个人的出行方式选择行为分为2个阶段，分别为出行者选择肢集合的生成阶段(choicesetformulation)和补偿性选择过程(compensatorychoiceprocess)[6].如此便可很好地解决因阈值存在导致选择概率发生突变的问题，以更好地描述和理解出行者的选择行为过程，提高预测精度，决策流程图见图1.

图1　出行方式选择决策流程

1.3模型假设与基础

根据模型理论与建立思路，进行相应的假设与变量、参数等的设定如下.

假设模型中供出行者选择的所有选择肢的集合为M;Pnj为选择肢j被出行者n选择的概率；向量Xnj=(Xnj1,Xnj2,…,Xnjk)为选择肢j的属性变量；向量Tnj=(Tnj1,Tnj2,…,Tnjk)为选择肢j属性变量相应的阈值；向量β=(β1,β2,…,βk)属性变量参数；An为出行者n对每个选择肢j进行筛选后得到的选择肢集合，当选择肢属性变量均满足相应阈值要求时则该选择肢进入选择肢集合.

由此，所有选择肢可组成多种选择肢集合，每种集合以一定的概率出现，将所有可能出现的集合作为一个元素构成一个集合.同时不会出现出行者没有任何选择即G为空集的情况.所以不难分析出，若集合M有m个元素，则集合G的元素个数为2m-1.如M={A1,A2}，则：G={(A1),(A2),(A1,A2)}..

1.4选择第一阶段：选择肢集合生成

由于研究者并不能确定阈值的具体数值，且出行者社会经济特征的不同或者选择环境的影响，阈值存在差异性，故在本文所建立的模型中假设阈值是一个随机变量.同时需要考虑到的特征变量如费用、时间等变量具有非负性，假设阈值服从对数正态分布Tnjk～1 g-N(μnjk,σnjk2)，阈值之间相互独立，协方差为0.

假设选择集合为M,出行者n需基于阈值对这m个选择肢进行筛选，超过阈值限制的选择肢将被排除.假设选择肢j(j∈M)共有k个特征变量，基于合取规则，需要将这k个特征变量与相应阈值进行比较，只有满足以下条件[7].

(2)

(3)

选择肢j才能被接受进入选择肢集合An.

阈值服从对数正态分布Tnk～1 g-N(μnk,σnk2)，由此选择肢j能够被出行者n接受，成为选择肢集合An中的元素的概率为

(4)

式中：Xnj,Tn分别为选择肢j的特征变量向量及阈值向量；Pnj1为k个特征变量中第l个特征变量值Xnj1小于阈值Tni的概率.

出现出行者n的选择肢集合An=Ø的情况的概率为

(5)

选择肢集合为空集应在模型的第一阶段将该情况排除.

集合G为所有选择肢集合的可能组合中选择肢集合An的概率计算公式如下.

(6)

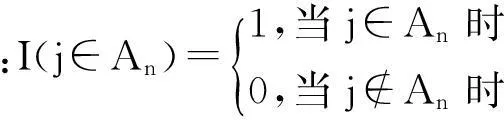
1.5第二阶段：补偿型选择过程

在Logit模型中，固定效用项Vni是特征变量Xni的函数.通常假设二者呈线性关系，即

(7)

在Logit或者NL等模型中，均假设未知参数为固定常数，每个人的特征向量参数都相同.Mixed-Logit模型假设特征变量的参数向量β为随机向量，服从某种分布，假设概率密度函数为f(β).结合MNL模型的概率公式可以得到Mixed-Logit模型的选择概率计算公式如下.

(8)

式中：Lni(β)为Logit模型对出行者n选择选择肢i的概率

(9)

结合以上3式，最终Mixed-Logit模型的选择概率可写为以下形式.

(10)

式中：Xnj=[Xni1,Xni2,…,Xnik,…,Xniκ]为选择肢i对于出行者n的特征变量；β=[β1,β2,…,βk]'为各个特征变量所对应的未知参数向量；f(β)为联合分布密度函数.

假设特征变量参数服从正态分布：

(11)

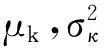
由此可得在Mixed-Logit模型中，出行者n在选择肢集合中选择选择肢i的概率选择公式，为了与最终出行者n选择选择肢i的表达式区分开，本文将Mixed-Logit模型的选择概率表达如下.

(12)

式中：PMLni为在Mixed-Logit模型出行者选择某选择肢的概率;f(β)为随机参数的概率密度函数.

根据文中模型可知，若选择肢i在出行者n的选择肢集合An中，则利用第二阶段的选择概率计算，否则其选择概率为零.出行者n对选择肢i的选择概率即为所有可能的集合中的选择肢i被出行者n选择的概率之和.

(13)

式中：Pni(i/An)为在给定选择肢集合An时出行者n选择选择肢i的概率

(14)

1.6半补偿型方式划分模型选择概率公式

综合以上的计算公式，可以得到最终基于Mixed-Logit的半补偿型方式划分模型中出行者n对选择肢i的选择概率计算公式如下.

(15)

式中：

2模型应用实例

2.1选择肢及特征变量的确定

2013年4月在北京部分公司针对上班族在基于商务活动的目的时的方式选择行为进行了SP调查.选择肢分别为城市轨道交通(SUBWAY)、公交车(BUS)、出租车(TAXI)以及私家车(CAR).在选择肢属性变量选择上，由于出行者的方式选择行为往往会受到众多因素的影响 .本文模型获取数据来源是基于对北京市上班族的问卷调查，根据《北京市居民出行调查报告》对影响出行选择行为的影响因素进行分析[8]，以此为依据确定本文模型的属性变量.

2.2出行方式选择行为调查

通过参考国内外相关文献中对样本量的需求和调查方法[9]，并结合本文模型设定的属性变量个数以及参数个数，本文采用SP调查方法获取标定参数的数据，调查对象为北京市上班族，调查一共发放272份问卷，其中回收有效问卷150份问卷，共计900组有效数据.以下为本次SP调查问卷的设计过程.

SP调查目的是得到被调查者对选择肢属性在不同水平下的偏好程度，首先需要根据模型的变量设置来确定出行方式的属性及相应的水平值，然后进行情境设计，得到SP调查问卷.

1)选择肢属性的确定根据模型属性变量的设定和SP调查属性个数3～4个为宜，本文在调查时将出行时间分为接近时间与在车时间(接近时间=步行至站点时间+等候时间).最终本次SP调查4种交通方式的属性设置见表1.

表1　SP调查属性

2)水平值的确定本次SP调查假设出行者的出行目的及出行距离均一致，根据北京居民平均出行距离以及机动化交通方式的竞争范围，将出行距离上设置在8km，根据模型的目的以及实际情况(调查地点为北京)，各方式出行费用范围依据出行距离(8km)得到，其中地铁票价进行调整以体现费用对轨道交通选择的影响，私家车出行费用范围主要通过油耗费用及现行停车费率得到，最终本次SP调查设置的各属性变化范围见表2.

表2　属性变化范围表

注：时间单位为min;费用单位为元.

在确定属性及水平值后，本次SP调查根据《均匀设计与均匀设计表》得到相应的情景组合[10].并从各种交通方式的不同情景进行随机组合，随机组合出大量的情景.再结合需要采集的个人信息，即可设计出大量不同的调查问卷.

2.3模型参数估计

本文采用马尔科夫链蒙特卡罗算法进行参数估计，并通过Matlab平台来实现该算法.为避免Mixed-Logit模型中的积分，简化运算，VanDyk和Meng在《TheArtofDataAugmentation》中提出将数据扩张技术(dataaugmentation)与马尔科夫链蒙特卡罗算法相结合来避免积分计算.

具体做法是在每次随机产生参数矩阵，同样产生随机参数β，并且求得随机参数β'在其分布参数μ',σ'下取值β下的条件概率密度：

(16)

计算似然算子时，将Mixed-Logit的概率计算转换为Logit模型的概率计算，避免积分，最后通过乘上条件概率密度Pdfκ即可得到最终的似然算子[11].

基于该方法，本文模型参数最终的估计过程如下.

假设需要估计的参数为θ=(μk,σk,β,μβ,σβ)，其中(μk,σk)为阈值的分布参数，β特征变量参数(包括时间、费用、拥挤度参数)，(μβ,σβ)为随机特征变量参数的分布参数.

步骤1随机产生参数θK.初始化K=1，θ1=0,K>1时,通过θκ～N(θκ-1,σ)(其中σ根据参数范围设定为常数)得到随机参数组θK.

步骤2根据半补偿型方式划分模型的计算公式将参数θK代入首先得到不同选择肢集合的概率，即P(An(G)，然后进入选择第二阶段基于参数求得β,求得Logit选择概率PLni,然后将两阶结合得到Pni.并求得β中在θk中其分布参数下取随机参数βk的概率密度Pdfκ.

步骤3记样本容量为N，选择肢数目为m，定义辅助变量为yni，且有

(17)

则似然函数为

(18)

对上式取对数并与Pdfk相结合得到最终似然算子如下

ln(PdfK)

(19)

步骤4令

(20)

进行如下判断：当τ≥0时,θ'K=θK；当τ<0时，产生服从U(0,1)的随机数t，当τ≥ln(t)，θ'K=θK,否则θ'K=θ'K-1,LL(θK)K=LL(θK-1)K-1.

步骤5重复上述过程R次后，求其平均值即为最终参数估计值，即有下式

(21)

本文利用Matlab平台实现上述算法并结合SP调查得到的数据，最终得到参数估计结果见表3，表4.

从参数标定结果来看，大部分参数估计值在置信水平为95%的区间内变化范围较小，在可接受范围内，由此可说明参数估计值可靠性较高.

从参数估计值的结果来看， SUBCONST的值相对其他的哑元变量更大，说明在各种交通方式均可到达目的地时，出行者更加倾向于选择城市轨道交通；公交的哑元变量为负值，根据分析可能是由于公交的服务质量相对较低.其次，性别的参数估计结果体现了男女对于舒适度，时间敏感性以及费用等的重视程度均不相同.

时间与费用随机分布的参数中均值为负数，说明时间与费用的增长会带来负效用，与实际情况相符，同时可以看出时间与费用对出行选择的影响程度是最大的.

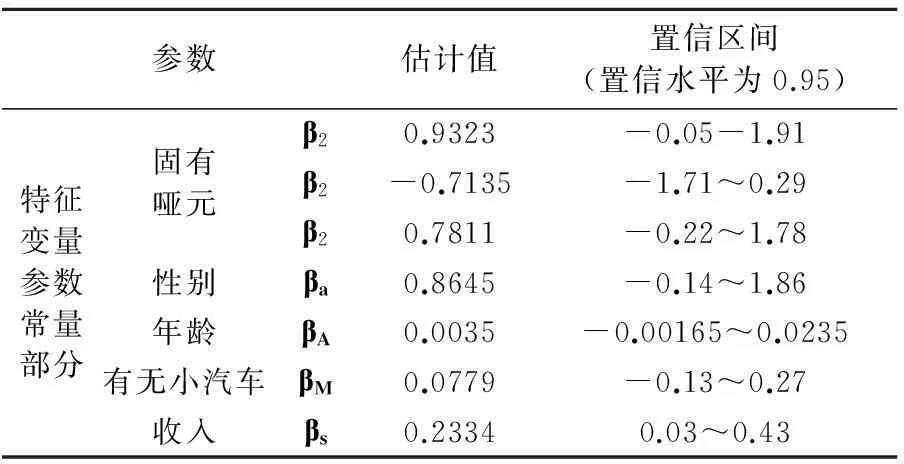
表3　模型参数估计结果表1

表4　模型参数估计结果表2

阈值方面，求得时间、费用、拥挤程度的阈值的期望值分别为77.5min,31.31元，3.97，虽然在进行特征变量取值时将拥挤程度为离散值，但是其结果可以解释为人们对拥挤程度的忍受程度在“无座”与“拥挤，感觉不适”之间，在拥挤无座状态下时一些人可能可以忍受，但当拥挤程度濒于较拥挤且会感觉不适时人们可能就拒绝该交通方式.从时间、费用的分布参数同样可以发现出行者对时间、费用、拥挤程度均存在绝对要求，这也证实了在出行方式选择过程中会受到来自阈值的影响，并不完全遵守补偿性原则，存在非补偿性原则的特点，以往的方式划分模型的假设往往会存在人为误差，而本文所建立的模型很好地解决了这一问题.

2.4模型预测结果对比

本次模型的验证主要采用命中率法.该方法的原理就是将模型推算得到的结果与实际的出行方式选择结果进行对比，求得其吻合程度(即命中率).

为将本文模型与Logit模型对比，根据样本数据求得MNL模型参数的标定结果见表5.

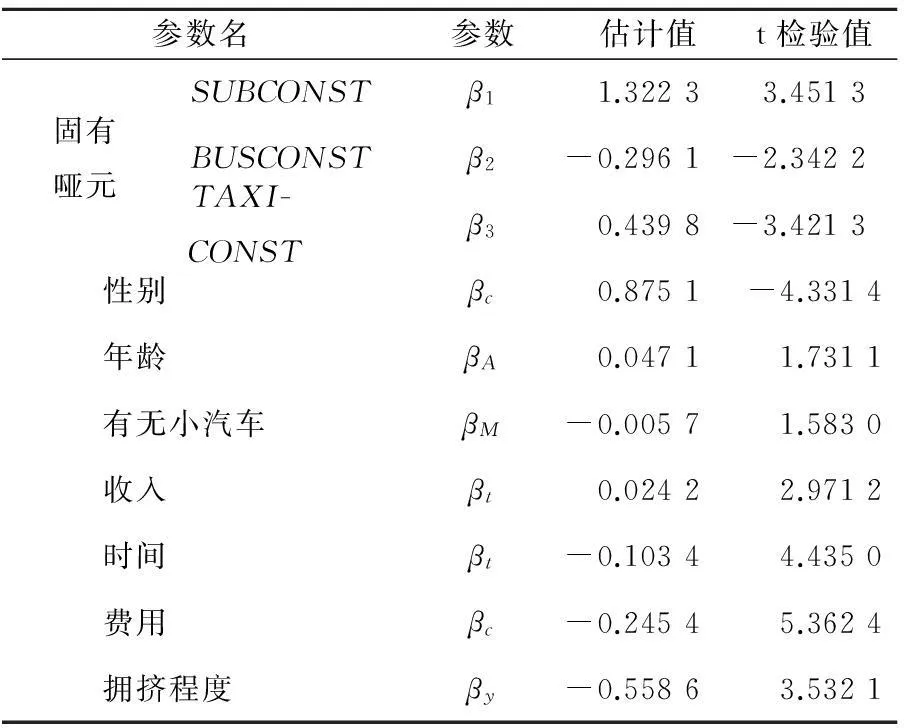
表5　MNL模型参数估计结果

在得到标定参数后，采取部分样本数据对两个模型的命中率进行对比，最终得到的结果见表6.

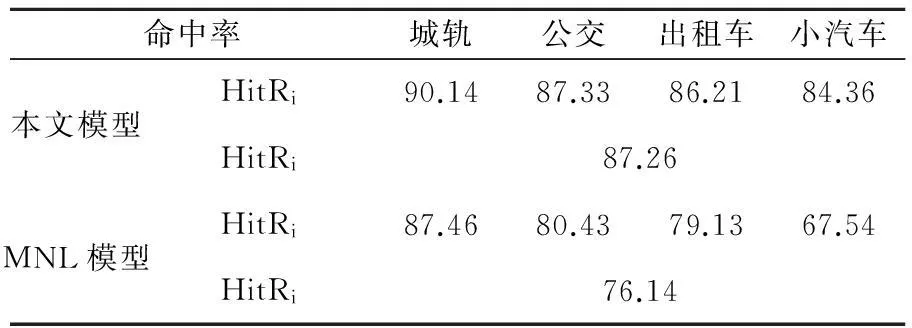
表6　模型预测结果对比　%

由表6可知，本文中的模型预测结果的总体命中率达到了87.26%，高于80%，其预测精度在可接受范围内.相比较于MNL模型的76.14%可以看出，本文所建立的方式划分模型具有明显的优势.

3结束语

通过对离散选择模型与交通方式选择过程进行分析，引入阈值概念建立了基于Mixed-Logit的半补偿型方式划分模型，并采用SP调查获取数据，对建立的模型进行了标定并与MNL进行对比，结果显示模型具有较高精度，能够很好地描述交通方式选择行为，反映时间、费用等阈值的影响，在很大程度上克服了IIA特性、喜好随机性限制以及补偿假设等重大缺陷，更好地描述人们的方式选择行为，提高了模型的预测精度.

参 考 文 献

[1]TRAIN K E.Discrete choice methods with simulation [M].London:Cambridge University Press,2003.

[2]SWAIT J.A non-compensatory model incorporating attribute cutoffs[J].Transportation Research Part B:Methodological,2001,35(10):903-928.

[3]BASAR G,BHAT C.A parameterized consideration set model for airport choice: an application to the San Francisco Bay Area [J]. Transportation Research Part B, 2004, 38:889-904.

[4]CANTILLO V,JUAN de D. A semi-compensatory discrete choice model with explicit attribute thresholds of perception [J]. Transportation Research Part B: Methodological, 2005, 39(7):641-657.

[5]姚丽亚, 孙立山, 关宏志. 基于分层Logit模型的交通方式选择行为研究[J].武汉理工大学学报,2010,31(4):738-741.

[6]MANSKI C,LERMAN S.The estimation of choice probabilities from choice based samples [J].Econometrica, 1977, 45:1977-1988.

[7]关宏志. 非集计模型-交通行为分析的工具[M].北京：人民交通出版社，2004.

[8]北京交通发展研究中心.北京市2012年交通运行报告[R].北京：北京交通发展研究中心，2013.

[9]王树盛,黄卫,陆振波.Mixed Logit模型及其在交通方式分担中的应用研究[J].公路交通科技,2006,23(5):88-91.

[10]方开泰.均匀设计与均匀设计表[M].北京：科学出版社，1994.

[11]DAVID A,DYK V,MENG Xiaoli.The art of data augmentation [J].Journal of Computational and Graphical Statistics, 2001, 10(1): 1-50.

Research on Semi-compensatory Modal-split

Model Based on Mixed-Logit Model

XIAO Lin1，2)WEI Chong3,4)CHEN Xiaohong1，2)SHAN Xiaonian1,2)

中图法分类号：U491

doi:10.3963/j.issn.2095-3844.2015.01.024

收稿日期：2014-10-20

(SchoolofTransportationEngineering,TongjiUniversity,Shanghai201804,China)1)
(TheKeyLaboratoryofRoadandTrafficEngineering,
MinistryofEducation,Shanghai201804,China)2)

(SchoolofTrafficandTransportation,BeijingJiaotongUniversity,Beijing100044,China)3))

(CenterofCooperativeInnovationfor

BeijingMetropolitanTransportation,Beijing100124,China)4)

Abstract：Most of modal spit models were formulated based on the random utility theory that assumes that choice behavior of individuals completely follow compensatory rule; however some previous studies pointed that this assumption is strong, because individuals usually make decision dependent on some psychical thresholds. This paper proposes a semi-compensatory modal-split model based on mixed-logit model combined with psychical thresholds. The proposed model has two stages, and the model generates the choice set using psychical thresholds and then calculates the choice probability by a Mixed-Logit model in order to overcome IIA property and limitation of taste variation. Based on the sample data obtained by SP survey, we estimated the proposed model using a Markov chain Monte Carlo algorithm combined with data augmentation technique. We tested this model using Hit-Ratio method and compared with MNL model. Results show that the performance of the proposed model is better than that of the MNL model.

Key words：modal split; Mixed-Logit model; semi-compensatory model; threshold; SP survey

*中央高校基本科研业务费资助(批准号：2014JBM056)