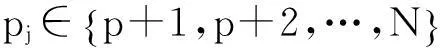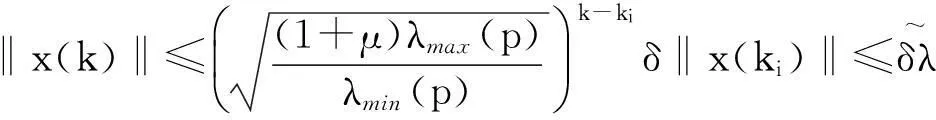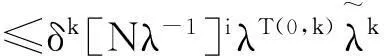一类复杂切换系统的可镇定性

一类复杂切换系统的可镇定性

白鹏

(兰州交通大学 数理学院, 甘肃 兰州 730070)

摘要：针对一类带有非线性脉冲及扰动的离散切换系统，给出了系统可控时的状态转移矩阵估计.通过状态转移矩阵估计和在给定切换频率下任意切换信号，得到了带有脉冲作用的平面离散切换系统的可镇定性.同时，当系统至少含有一个不可控子系统时，通过满足一定的切换频率，整个切换系统仍然是可镇定的.

关键词：切换系统; 可镇定性;脉冲作用及扰动

中图分类号：O322; O324 文献标志码：A

收稿日期：2014-11-08

作者简介：李强，男，liqiangxin@163.com

文章编号：1672-6197(2015)05-0061-03

Aclassofcomplexswitchingsystemstostabilization

BAIPeng

(SchoolofMathematicsandPhysics,LanzhouJiaotongUniversity,Lanzhou730070,China)

Abstract:We provided the state transition matrix estimation for a class of discrete switched systems with nonlinear pulse and disturbance. Through the state transition matrix estimation and under arbitrary switching signal of a given switching frequency, we got the stability of planar discrete switched systems with pulse function. At the same time when the system contained at least one uncontrolled subsystem, the whole switching system was still stabilizable by satisfying certain switching frequency.

Keywords:switchingsystem;stabilization;impulseeffectsanddisturbance

切换系统[1]是由若干个相互作用相互影响的连续系统和离散系统组成，是混杂系统[2]中应用最广泛的一类系统.稳定性可以说是系统中的最基本的性质，在切换系统的研究中，切换系统的稳定性[3]也是研究最为集中的问题，而且取得了一大批研究成果.1999年，DanielLiberzon和A.StephenMorse在同年10月的控制系统杂志上发表了第一篇有关切换系统的稳定性及其设计的综述文章，比较全面地阐述了切换系统稳定性研究的基本问题.

本文根据非线性脉冲及扰动作用的平面离散时间线性切换系统[3-7]，对所有子系统均可控情况，确定了给定切换频率及有界脉冲条件下系统的可镇定性；当系统至少含有一个不可控子系统时，通过满足一定的切换频率，系统仍然是可镇定的.

1系统描述

考虑如下离散时间切换系统：

(1)

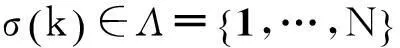
若存在反馈增益K使得u(k)=Kσ(k)x(k),则系统(1)可表示为下面的闭环系统：

x(k+1)=(Gσ(k)+Hσ(k)Kσ(k))x(k),k≠kj

其中(Gσ(k)+Hσ(k)Kσ(k))表示状态转移矩阵.

当系统(1)可控时，首先对状态转移矩阵(G+HK)进行估计.

引理1[8]对于系统(1)若存在G∈R2×2和H∈R2×m常数矩阵，使得(G,H)是可控的，则存在K∈Rm×2，对任意0<λ<1，有下面的结论成立:

‖(G+HK)k‖≤Nλk-1,k≥0

其中N>0是常数，与λ值无关，并且可以通过G,H和n估计出.

引理2[8]对于系统(1)，如果(G,H)是不可控的，并且闭环系统是成立的，那么对于任意给定的反馈增益K, 都存在常数μ>0使得下式成立：

‖x(t)‖≤c‖x(0)‖，c>0，∀t>0

则称切换系统是渐近稳定的.

2切换系统的镇定性

在线性反馈律u(k)=Kσ(k)x(k)(k≠kj,j=1,2,…)下，系统(1)形如如下的闭环系统：

(2)

定义切换频率为

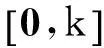
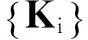
(3)

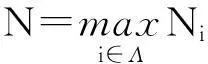
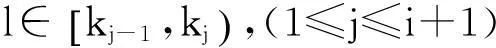
(4)

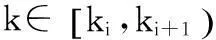
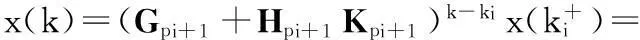
(Gpi+1+Hpi+1Kpi+1)k-kiF(pi,pi+1)(Gpi+1+Hpi+1Kpi+1)ki-ki-1F(pi-1,pi)(Gpi-1+

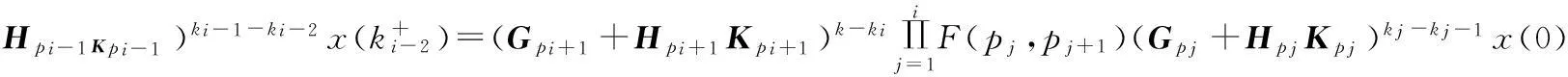
由假设1，我们得

‖F(pj,pj+1)‖·‖x(0)‖≤δiNi+1λk-i-1‖x(0)‖≤(λc)βk‖x(0)‖

由λc<1，β=1-α>0，对任意的f<1的切换信号，系统(1)是渐近稳定的.定理1证明完成.

下面考虑系统(1)存在可控子系统，也存在不可控子系统的情况.

假设2(G1,H1),(G2,H2),…,(Gp,Hp)是不可控子系统,

(Gp+1,Hp+1),(Gp+2,Hp+2),…,(GN,HN)是可控子系统，其中1≤p

T(0,k)≥γk，k≥0

(5)

考虑系统不可控的情况，对任意给定的反馈增益Ki(1≤i≤p)，总存在正定对称矩阵Pi和正常数μi使得下式成立:

(Gi+HiKi)TPi(Gi+HiKi)-Pi<μiPi，1≤i≤p

(6)

设

(7)

‖x(k)‖≤‖(Gpi+1+Hpi+1Kpi+1)k-ki‖‖F(pi,pi+1)‖‖x(ki)‖≤δNλk-ki-1 ‖x(ki)‖

(8)

(9)

由式(8)，(9)可得

3数值计算

考虑切换系统(1)，其中σ(k)=1,2,3,并且

可以看出，对于i=1,2,(Gi,Hi)是可控的, (G3,H3)是不可控的.

4结束语

本文主要研究了一类带有非线性脉冲及扰动的切换系统可镇定性问题，给出了系统全部可控时的状态转移矩阵估计，通过状态转移矩阵估计得到了在给定切换频率的任意切换信号下，得到带有脉冲作用的平面离散切换系统的可镇定性.同时给出了系统部分可控时系统的镇定性.

参考文献:

[1]YangH,JiangB.Onstabilityofnon-linearandswitchedparabolicsystems[J].IETControlTheoryAppl.，2014,7(5):749-758.

[2]GuoP,WangY.Stabilityanalysisforaclassofswitchedlinearsystems[J].Asian.Control， 2013,14(3):817-831.

[3]郑刚,谭民,宋永华.混杂系统的研究进展[J].控制与决策,2008,15(1):7-16.

[4]杨磊,李俊民.一类线性切换系统的能控性和能观测性的充要条件[J].系统工程与电子技术,2012,25(5):588-616.

[5]NarendraKS,BalakrishnanJ.AcommonLyapunovfunctionforstableLTIsystemswithcommutingA-matrices[J].IEEETransactiononAutomaticControl,2012,39(12):2469-2471.

[6]ZhuXL,YangGH.Jensenintegralinequalityapproachtostabilityanalysisofcontinuous-timesystemswithtimevaryingdelay[J].IETControlTheoryApplication, 2008,2(6):524-534.

[7]ZhaoS，SunJ.Controllabilityandobservabilityfortime-varyingswitchedimpulsivecontrolledsystems[J].Internationaljournalofrobustandnonlinearcontrol.，2010,20(12):1313-1325.

[8]SeatzuC,CoronaD,GiuaA,et al.Optimalcontrolofcontinuous-timeswitchedaffinesystems[J].IEEEtransactionsonautomaticcontrol,2012,51(5):726-756.

(编辑：姚佳良)