近景摄影测量中基于本质矩阵分解的相对定向算法

近景摄影测量中基于本质矩阵分解的相对定向算法

李云雷1，蒋灵搏2

(1.山东理工大学 机械工程学院，山东 淄博 255049；

2.山东工业职业学院 机电工程系，山东 淄博 256414)

摘要：针对近景摄影测量中多基线、大倾角交向摄影相对定向困难的情况,提出了基于本质矩阵分解的相对定向算法.首先,从共面条件方程出发,推导出本质矩阵与相对定向参数的内在联系,然后给出由基础矩阵计算本质矩阵的方法;再利用本质矩阵的奇异值分解计算出表征相对定向关系的旋转矩阵和平移矢量.箱体表面三维重建的近景摄影测量实验表明,提出的相对定向算法在实践中是稳定可靠的.

关键词：近景摄影测量; 相对定向; 本质矩阵; 基础矩阵

中图分类号：P234.1 文献标志码：A

收稿日期：2014-10-11

作者简介：白鹏，男，1632301432@qq.com

文章编号：1672-6197(2015)05-0057-04

Relativeorientationalgorithmbasedonessentialmatrix

decompositioninclose-rangephotogrammetry

LIYun-lei1,JIANGLing-bo2

(1.SchoolofMechanicalEngineering,ShandongUniversityofTechnology,Zibo255049,China;

2.DepartmentofElectricalandMechanicalEngineering,ShandongVocationalCollegeofIndustry,Zibo256414,China)

Abstract:Relative orientation becomes a difficulty in multi-baseline convergent photography with big rotation angles. Therefore, an algorithm is presented, in which the orientation parameters come from the decomposition of the essential matrix. First, the relationship between the essential matrix and the orientation parameters is derived by the coplanarity condition, and then the calculation from the fundamental matrix to the essential matrix is introduced. Next, the rotation and translation between two images are calculated by singular value decomposition(SVD) of the essential matrix. At last, the algorithm is used in the 3D reconstruction of the box surface, and the result shows that it is stable and reliable.

Keywords:close-rangephotogrammetry；relativeorientation；essentialmatrix；fundamentalmatrix

相对定向是数字近景摄影测量中的关键技术之一,目的是在立体像对所在的局部坐标系中,确定一张像片相对于另一张像片的旋转矩阵和平移矢量[1].传统的近景摄影测量要求摄影时,像片对的主光轴要位于或近似位于一个平面内[2-3],且两个主光轴近似平行或是呈较小的倾角.在以上情况下，连续像对的相对定向算法一般是将代表旋转矩阵的3个旋转角初值设定为零，平移矢量中的首个分量作归一化处理，后两个分量用小角度表达，且初值也设定为零，然后通过方程迭代最终可收敛于正确解.然而随着高性能数码相机在近景摄影测量中的广泛应用,利用“手持”相机的多基线交向摄影越来越普遍,而且近景影像的倾角比较大,此时摄影的基线、相对方位就难以符合传统近景摄影测量的要求[4].

数字近景摄影测量除了用于测绘工程领域外,在汽车、造船、航空工业以及建筑、文物保护和医学等领域也有广泛的应用前景.因此,其拍摄对象的形状会千变万化,摄站的布置随之变得十分复杂,立体像对中两张像片之间的关系大多是任意角度的旋转,这就使得相对定向比较困难,甚至无法实现[4].本文提出一种基于本质矩阵分解的相对定向算法,可以获得比较稳定的相对定向参数.

1本质矩阵的推导

这里从摄影测量学中的共面条件出发,推导本质矩阵与相对定向参数的关系.

图1　相对定向模型

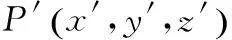
(1)

(2)

(3)

2本质矩阵的求解

(4)

结合式(3)和式(4)可得

(5)

基础矩阵的求解主要分为线性算法、非线性算法和鲁棒估计法.线性算法有7点法、归一化8点法、线性最小二乘法;非线性算法有极线距离迭代法、梯度迭代法及非线性参数空间优化法等;鲁棒估计法常用的有M-Estimators,最小平方中值(Least Median Squared，LMedS)和RANSAC(RANdom Sample Comsensus)等[5-7].线性和非线性算法要求两张像片的同名像点之间严格匹配,否则会产生较大误差,而鲁棒估计法能够容纳部分误匹配点对,具有很强的稳定性.

近景工业摄影测量中,一般先选取部分已知的正确匹配的同名点对实现相对定向，然后再对其他像点匹配,最后进行整体光束平差.故根据同名像点个数n的多少(要求n≥8),本文选用归一化8点法并结合线性最小二乘法计算基础矩阵.有关算法的内容可参考文献[5-7].

3本质矩阵分解计算旋转矩阵和平移矢量

确定了本质矩阵E之后,再对其进行奇异值(SVD)分解

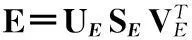
(6)

则旋转矩阵R和平移矢量t的值为

R=UEWVTE或R=UEWTVTE

(7)

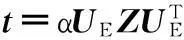
(8)

其中,α为不等于零的任意常数.W和Z分别为

(9)

4箱体的近景摄影测量实验

4.1　实验方法

实验的目的是利用相对定向算法重建箱体表面的三维结构.相机型号为尼康D3200,等效焦距27mm,摄影距离约6m.图2是从3个不同角度获得的像片,在箱体表面及周围空间布置了人工回光反射标志.利用图像处理的相关算法,提取了所有圆形标志点中心的像素坐标.将标志点分为两组,箱体表面3排共计15个标志点用于表面的三维重建,其余标志点用来实现相对定向.

(a)像片1

(b)像片2

(c)像片3 图2　箱体表面的近景摄影测量实验

4.2　实验结果

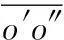
采用两种定向算法进行对比分析，算法1是传统近景摄影测量中的连续像对相对定向，5个参数的初值设定为零，迭代求解；算法2是本文的基于本质矩阵分解的相对定向算法.

结果显示，像片1和2与像片3和2这两组，因交向倾角较小，所以两种算法的解是接近的；像片3和1这一组，因交向倾角过大，算法1的迭代解严重偏离实际情况，而算法2的解经过三维重建检验是正确的.

依据像片中15个标志点的像素坐标和相对定向参数,进行空间前方交汇解算标志点的三维模型,但还需加入一个比例因子.实验前已测得左上角和右下角标志点中心之间的实际距离,与模型中的两点距离对比,即可得到比例因子,进而求得所有标志点的真实三维坐标.

依据表1中算法2的3组相对定向参数,依次重建出箱体表面在像片1、2、3的相机坐标系中的三维形貌,并对标志点作了平面拟合处理,如图3所示.梯度变化反映了标志点沿相机z轴的坐标大小.与图2中的3幅像片对照可知,拟合平面直观反映了箱体表面的形貌.这说明本文提出的相对定向算法是稳定可靠的,特别是像片3和1这一组的交向角已接近60°,却依然能获得正确解.

表1　三组立体像对的相对定向参数

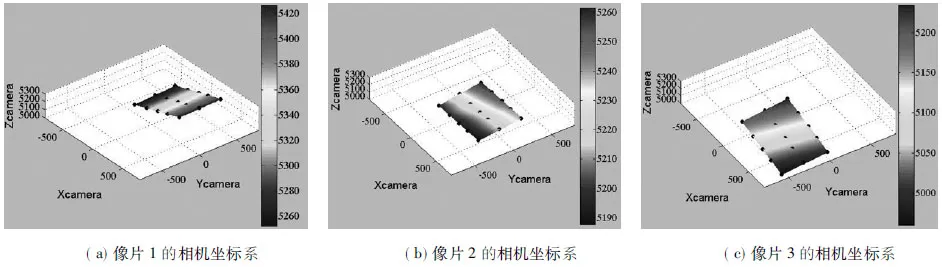
图3 　箱体表面在三个相机坐标系下的三维形貌(单位： mm)

5结束语

本文提出的基于本质矩阵分解的相对定向算法,较好地解决了数字近景摄影测量中多基线、大倾角交向摄影难于定向的问题.箱体表面近景摄影测量实验的结果表明该算法在实践中是切实可行的,获得的相对定向参数结果稳定可靠.同时，在近景摄影测量的全过程中,稳定的相对定向算法有助于增加后续匹配环节的成功率，并为光束法平差提供可靠的初值.

参考文献：

[1]LuhmannT,RobsonS,KyleS, et al.Closerangephotogrammetry:principles,techniquesandapplications[M].Dunbeath:WhittlesPublishing, 2006.

[2]陆珏, 陈义, 郑波. 多基线近景摄影测量连续像对相对定向[J]. 同济大学学报：自然科学版, 2010, 38(3)：442-447.

[3]冯文灏.近景摄影测量物体外形与运动状态的摄影法测定[M].武汉:武汉大学出版社,2002.

[4]张祖勋,杨生春,张剑清，等.多基线数字近景摄影测量[J].地理空间信息,2007,5(1):1-4.

[5]HartleyR,ZissermanA.Multipleviewgeometryincomputervision[M]. 2nded.Cambridge:CambridgeUniversityPress,2003.

[6]HartleyRI.InDefenseofthe8-pointalgorithm[C]//Proceedingsofthe5thProc.InternationalConferenceonComputerVision.Boston:IEEEComputerSocietyPress,1995:1 064-1 070.

[7]蔡涛,段善旭,李德华.视觉基础矩阵估计方法的性能比较与分析[J].计算机科学, 2009,36(12),243-247.

(编辑：郝秀清)