一种基于改进粒子群算法的K-means算法

一种基于改进粒子群算法的K-means算法

林晓雪, 赵茂先

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

摘要：针对K-means算法对初始聚类中心敏感、算法容易收敛于局部解等问题，运用了增加飞行时间因子的粒子群算法，提高粒子群算法性能.利用改进的粒子群算法与K-means算法相结合，提高了基于粒子群算法的K-means算法性能．数值试验验证了提出算法的收敛性，且最优解的精度优于K-means算法、PSO算法和PSO-K算法．

关键词：K-means算法；粒子群算法；飞行时间因子； PSO-K算法

中图分类号：TP301.6 文献标志码：A

A K-means algorithm based on the improved

particle swarm optimization algorithm

LIN Xiao-xue, ZHAO Mao-xian

(College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, China)

Abstract：Considering K-means algorithm was sensitive to the initial cluster centers and easy to converge to local solution and other issues, we increased flight time factor to improve particle swarm algorithm performance. The improved particle swarm algorithm and K-means algorithm were combined to improve the performance of K-means algorithm based on particle swarm optimization. Numerical experiments verified the proposed convergence of the algorithm, and the optimal solution accuracy was better than K-means algorithm, PSO algorithm and PSO-K algorithm.

Key words： K-means algorithm；PSO algorithm；flight time factor；PSO-K algorithm

K-means算法[1]是基于划分的经典聚类算法，具有容易理解、实现简单、收敛速度快等优点，但由于局部极值点的存在以及启发算法的贪心性，使得传统K-means算法有对初始聚类中心敏感、极易收敛于局部极值的缺点．目前，针对初始聚类中心的选取，许多研究者提出了不同改进算法．Jim等[2]提出了一种快速找到聚类中心的算法，该算法使用聚类中心的位移拒绝不可能的候选点，算法缩短了计算时间．Aliasa等[3]提出了修改后的移动K均值算法用来解决分割问题，修改后的算法是找到最近的中心为每个像素的更好聚类中心．Merwe等[4]率先提出用粒子群(Particle Swarm Optimization，PSO)算法解决聚类问题，文章介绍了粒子群算法是如何连接各个聚类中心，如何更好的实现K-means算法．Chen等[5]通过粒子群算法寻找聚类中心，根据聚类中心对粒子进行位置编码．Niknam等[6]提出了基于粒子群算法、蚁群算法和K均值聚类分析的高效混合的方法．

在分析上述研究成果和K-means算法存在缺陷的基础上，本文提出一种基于自适应飞行时间因子PSO算法的K-means算法．通过采用自适应飞行时间因子的PSO算法，动态调整粒子的飞行时间，避免了PSO算法中粒子出现早熟收敛的现象，消除K-means算法对初始聚类中心选取的依赖性，得到全局最优的N个聚类中心，然后以此为初始聚类中心执行改进的算法获得理想的聚类划分．

1基本算法简介

1.1　K-means算法

K-means算法的基本原理是基于划分的聚类算法，给定一组数据集X，数据总数n，首先随机地选取k个初始聚类中心(聚点)，把每个对象分配给离它最近的聚点，从而得到一组聚类．然后，计算每个聚类的均值作为新的聚点，并把每个数据重新分配到最近的聚点，循环执行这一过程，直到满足终止条件结束算法．

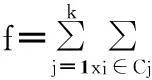
1.2　PSO算法

粒子群优化算法是一种基于群体智能方法的进化计算技术，最早由Kennedy和Eberhart[7]于1995年提出．粒子群算法就是粒子在d维空间搜索一个目标函数的最优解，在该空间中有N个粒子，粒子具有位置Zr和速度Vr，每个粒子的位置Zr代表了一个潜在解．将Zr代入目标函数就可以算出其适应度，根据适应度的大小来衡量解的优劣．第r个粒子目前自身搜索到的最好位置(pbest)为Pr，所有粒子目前搜索到的最优位置(gbest)记为Pg．最早期的PSO算法通过下面的公式来更新自己的速度和位置：

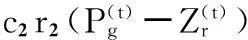
(1)

(2)

其中t是迭代次数；r1和r2为[0,1]之间均匀分布的随机数，以增加搜索随机性和种群的多样性；c1和c2是学习因子，也称加速因子，代表将每个粒子推向pbest和gbest位置的统计加速项权值．

为了提高基本PSO算法的性能，Shi等[8]提出了带有惯性权重因子w的粒子群算法，后来称这个改进的算法为标准粒子群算法(Stand Particle Swarm Optimization，SPSO)．SPSO算法将基本PSO算法中的速度更新公式改为下式：

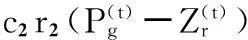
(3)

位置更新公式与基本PSO算法相同．上式中w称为惯性权重因子，是一个非负数，用来控制粒子的全局搜索能力与局部搜索能力之间的平衡．w较大时，粒子搜索全局空间的趋势较大，有能力探索新的区域，使算法全局搜索能力加强；反之w较小时，粒子局部搜索能力较强．w适中时PSO算法找到全局最优解的机会较大，鉴于以上分析，Shi等让w随迭代次数而线性递减：

(4)

其中wmax为惯性权重初始值；wmin为惯性权重终值；tmax为最大迭代次数；t为当前迭代次数．实验表明，这种改进明显改善了算法的性能，因此后来的改进都在SPSO的基础上进行的改进．

2PSO-K算法

由于K-means算法容易受初始聚类中心选取的影响，算法易收敛于局部极值．针对K-means算法的缺陷，不少学者提出了将优化算法与K-means算法相结合的算法，基于粒子群算法的k-means算法(PSO-K算法)是一种用粒子群算法的思想来解决聚类问题的优化算法，算法在一定程度上克服了K-means算法的缺陷．

2.1　PSO-K算法原理

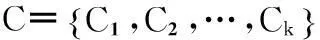
对于每个聚类中心的计算公式和样本集总的类间离散度和公式如下：

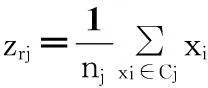
(5)

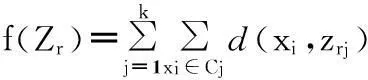
(6)

粒子的适应度按照公式(6)计算．其中Zr为第r个粒子(1≤r≤N)，N为粒子个数，zrj为第r个粒子的第j个类的聚类中心位置，d(xi,zij)为第i个样本数据到对应聚类中心的距离．聚类准则函数f(Zr)为各类样本到对应聚类中心的距离总和，也就是粒子的适应度函数．这里d(xi,zrj)为欧式空间距离．距离公式、粒子的速度和位置更新公式如下：

d(xi,zrj)=‖xi-zrj‖

(7)

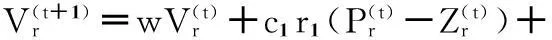
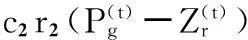
(8)

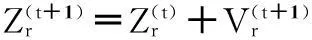
(9)

当聚类中心确定时，聚类的划分由最邻近法则确定，即每个数据优先划分到离它最近的聚类．

2.2　PSO-K算法步骤

(1)种群初始化．给定样本总数n，维数d，聚类个数k，先将每个样本随机指派为一类，作为最初的聚类划分，根据公式(5)计算各类的聚类中心，作为粒子的初始位置编码，初始化粒子速度，计算粒子的适应度．反复进行N次，共生成N个初始粒子；

(2)根据公式(6)、(7)计算每个粒子的适应度值；

(3)对每个粒子的适应度值和它所经历的最好位置Pr的适应度值比较，如果更好，更新Pr；

(4)对每个粒子的适应度值和群体所经历的最好位置Pg的适应度值比较，如果更好，更新Pg；

(5)根据公式(4)、(8)和(9)更新粒子的速度和位置；

(6)根据K-means算法中的最邻近法则，将每个样本重新归类，得到新的聚类划分；

(7)判断是否满足终止条件，如果满足输出最优解；否则返回(2)．

终止条件为粒子群的最好适应度值在给定的迭代数内几乎不改变或达到给定最大迭代次数．

3改进的PSO-K算法

3.1　自适应飞行时间因子的PSO算法

最基本的PSO算法中粒子的位置更新公式为(2)，现在增加飞行时间因子T，T表示第r个粒子的飞行时间，在基本PSO算法中T=1，因此PSO算法中的位置更新公式变为以下公式：

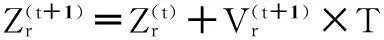
(10)

本文采用如下改进的飞行时间因子的计算方法：

T=F(αt,βt)=T0+αtTα-βtTβ

(11)

其中αt,βt分别表示种群多样性和种群进化度；T0为T的初始值，一般取0.8~1.0；Tα,Tβ用来调节αt,βt对飞行时间因子的影响程度．αt用来表示粒子的聚集程度，粒子越聚集，种群的多样性就越差；粒子越分散，种群多样性越好，算法就越不容易陷入局部最优解．αt的公式表示如下：

(12)

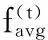
种群进化度指标βt．βt用来表示种群的进化程度，βt的公式表示如下：

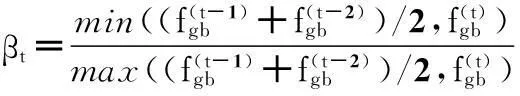
(13)

由公式(13)可知βt的取值范围，βt∈(0,1]．当βt=1时，表明算法没有进化，如果在给定的次数下算法都没有进化，可以认为算法找到了全局最优解或陷入了局部最优；当βt越小表示种群进化速度越快．

在进化初期βt值较小，此时粒子的飞行时间应该长点，即飞行时间因子T应较大．随着进化程度的减慢，βt值逐渐增大，粒子的飞行时间应该逐渐减小．若较为分散，粒子群的多样性就好，粒子群就不容易陷入局部最优．因此T的大小应该随着粒子群的聚集程度增大而增大，随着种群进化程度的降低而减小．即T随着αt的增大而增大，随着βt的增大而减小，从而可以将T表示为αt和βt的函数，即公式(11)所示．由于0<αt≤1,0<βt≤1，所以T0-Tβ

基于上述分析，基本的PSO算法就改为一种自适应改变飞行时间因子的PSO算法，相当于提高了PSO算法性能，增强了算法的收敛度．

3.2　改进的PSO-K算法步骤

本文提出的改进PSO-K算法是采用增加飞行时间因子的PSO算法，与K-means算法相结合从而提高PSO-K算法的收敛性．

改进的PSO-K算法具体步骤如下：

Step1 对粒子群进行初始化操作．给定固定参数w，c1，c2，vmin，vmax，T0，Tα，Tβ．从数据集X中随机选择k个中心点，将其作为粒子位置Zr的初值．同时初始化粒子的速度Vr、个体最优位置Pr和群体最优位置Pg．这一过程循环N次，可生成N个初始化粒子．

Step2 根据公式(6)、(7)，计算粒子的适应度值．

Step3 比较每个粒子的适应度值和它所经历的最好位置Pr的适应度值，如果更好，更新Pr．

Step4 比较每个粒子的适应度值和群体所经历的最好位置Pg的适应度值，如果更好，更新Pg．

Step5 根据速度公式(4)、(8)式和位置公式(10)-(13)分别更新粒子的速度和位置．

Step6 根据K-means算法中的最邻近法则，将每个样本重新归类，得到新的聚类划分．

Step7 判断是否满足终止条件，如果满足输出最优解；否则返回(2)．

终止条件为粒子群的最好适应度值在给定的迭代数内几乎不改变或达到给定最大迭代次数．

4实验结果及分析

本实验为了验证文中改进的PSO-K算法的有效性，采用的数据集为UCI数据集中经常用来测试聚类效果的数据集Iris数据集、wine数据集以及Breast Cancer数据集．

表1　测试数据集表

本文实验参数设置如下：粒子群的种群规模N=20，加速因子c1=c2=2，粒子群的最大迭代次数tmax=100，threp=4，threg=5，粒子群的适应度方差阈值threσ=0.1．文中增加飞行时间因子的PSO算法中，在经过多次试验之后，发现T0为0.8~1.0时算法效果较好，所以本文中T0=0.9．Tα和Tβ可以动态调整，一般较大的Tα会使算法容易跳过最优解陷入振荡状态，较大的Tβ会使算法容易陷入局部最优．经过多次实验，发现Tα在0.05~0.1之间取值，Tβ在0.4~0.6之间取值时算法性能较好，本次试验Tα和Tβ分别取值0.08和0.45．实验中将K-means算法、PSO-K算法与文中算法进行比较，每种算法分别执行20次，测试结果取其平均值．算法的聚类准确率以及适应度值的比较分别见表2、表3．

由表2可知，无论是对低维Iris数据集，还是高维wine数据集和Breast Cancer数据集， K-means算法的聚类准确率最低，PSO-K算法比K-means算

表2　K-means、PSO-K算法与文中算法聚类准确率比较

表3　K-means、PSO-K算法与文中算法适应度值比较

法聚类效果好一些，相比之下文中算法聚类效果最好．由表3可知，无论是对低维Iris数据集，还是高维wine数据集和Breast Cancer数据集， K-means算法的适应度值最大，PSO-K算法比K-means算法的适应度值小一些，相比之下文中算法的适应度值最小．适应度值越小则表明聚类划分得到的类内数据对象之间紧密程度越好，由此可知文中改进算法的聚类效果最好．

为了验证算法的收敛性能，对Iris数据集进行测试得到三种算法的收敛曲线图(图1)．

图1　三种算法的收敛曲线图

从图1中可以看出 K-means算法前期收敛速度最快，但算法容易收敛于局部解，PSO-K算法由于粒子群早熟收敛问题，收敛速度没有K-means算法收敛速度快．文中改进算法由于增加了自适应飞行时间因子，提高了PSO算法性能，同时又对早熟收敛的粒子执行变异操作，这样就增加了算法的收敛速度．所以文中算法的收敛性较理想．

5结束语

本文研究的基于粒子群算法的K-means算法是聚类分析研究的新的主流方向，通过采用自适应飞行时间因子的PSO算法与K-means算法相结合，提出了的改进的PSO-K算法．通过数值实验，文中算法比K-means算法、PSO-K算法具有更优的全局收敛性，进而验证了本文算法的可行性和有效性．然而与传统K-means算法相比，文中算法的运算时间有所增加，如何提高K-means算法精确度并同时保持较快的计算速度，是进一步需要研究的课题．

参考文献：

[1] Hartigan J A. Clustering Algorithms[M]. New York: John Wiley & Sons Inc, 1975.

[2] Jim Z C, Huang T J, Liaw Y C. A fast k-means clustering algorithm using cluster center displacement[J]. Pattern Recognition, 2009(42):2551-2556.

[3] Aliasa M F, Isa A M, Suaiman S A,etal. Modified moving k-means clustering algorithm[J]. International Journal of Knowledge-based and Intelligent Engineering Systems, 2012(16): 79-86.

[4] Merwe D W, Engelbrecht A P. Data Clustering using Particle Swarm Optimization[C]// Evolutionary Computation, 2003: 215-220.

[5] Chen C Y, Fun Y. Particle Swarm Optimization Algorithm and Its Application to Clustering Analysis[J].International Conference on Networks, 2004, 3(21): 789-794.

[6] Niknam T, Amiri B. An efficient hybrid approach based on PSO, ACO and k-means for cluster analysis[J]. Applied Soft Computing, 2010(10): 183-197.

[7] Kennedy J, Eberhart R. Particle Swarm Optimization[J]. International conference on neural network, 1995, 4(2): 1942-1948.

[8] Shi Y, Eberhart R. A Modified Particle Swarm Optimizer[C]// International conference on Evolutionary Computation Anchorage, 1998: 69-73.

(编辑：姚佳良)