Hilbert空间上的g-框架及单位分解

Hilbert空间上的g-框架及单位分解

赵云，陶常利

(山东科技大学 数学与系统科学学院,山东 青岛 266590)

摘要：g-框架是对框架理论进一步的补充和丰富，在实际应用上更具有灵活性.利用算子理论和泛函分析的知识完善g-框架的一些结果并讨论了g-框架的判定和求g-框架下界的方法.其次,给出了单位分解的几个性质,并进一步研究了它与g-框架的关系.

关键词：g-框架；单位分解；下界

中图分类号：O177.1 文献标志码：A

收稿日期：2014-12-09

作者简介：姜雨萌， 女，594245238@qq.com

文章编号：1672-6197(2015)05-0033-04

G-frame and resolution of the identity in Hibbert space

ZHAO Yun, TAO Chang-li

(College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, China)

Abstract:g-frame is the supplement and complement of the abstract frame theory,and have more flexibility in practical application. We improved some results of g-frame and discussed the judge of g-frames to provide a method for getting its lower bound.Secondly,some properties of resolution of the identity were given,and the relationship between g-frame and the resolution of the identity was further studied.

Key words:g-frame; resolution of the identity;lower bound

框架具有很多比较好的性质,使得它在函数空间、信号处理等领域都有重要的应用.框架的一个主要优点是给出一个框架,我们可以仅从它的一列复的框架系数就可以得到函数的特性并且对其进行重建.文献[1-4]对框架的理论和应用进行了详细的介绍.由于框架应用的广泛性,人们越来越热衷于对框架的研究,从而衍生出许多新的概念和应用.其中,南开大学的孙文昌教授通过对有界准投射算子族[5]、子空间框架[6-7]、伪逆框架[8]、斜框架[9-10]、外框架[11]等多种框架类型的研究,归纳它们的共同性质,从中提炼出了g-框架的概念[12-13].g-框架是抽象框架的推广,使得在用框架展开系数来表征函数空间方面更具有灵活性.单位分解是一个重要的研究方向,利用单位分解和g-框架的性质,可以得到一些有意义的结果.

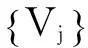
1关于g-框架的一些结果

首先,我们给出Hilbert空间中有关g-框架的几个概念[12].

∀f∈U

(1)

定义2若式(1)只考虑右端不等式,即

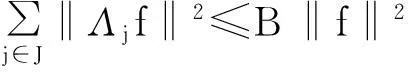
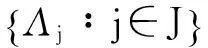
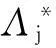
由文献[12]我们知道,S是U上的正定可逆的算子,满足AId≤S≤BId,且还满足重构公式

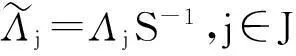
下面我们讨论g-框架的简单性质.

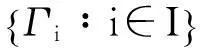
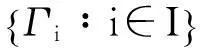
B1‖Λjf‖2

则

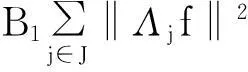
因此,

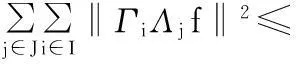
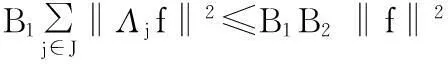
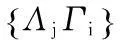
前面已经提到,g-框架是由多种类型的框架提炼而出的一种框架,因此,在实际应用方面,g-框架具有更多的选择和灵活性.我们根据文献[7]中有关子空间框架的研究,给出一种求g-框架下界的方法.

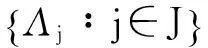
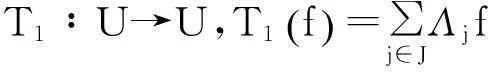
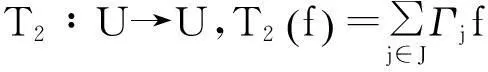
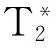
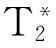
因此,

即

g-框架作为抽象框架的一种推广,无论是在理论研究方面,还是在实际应用中,都起到了不可替代的作用.那么,g-框架的判定就显得尤为重要.

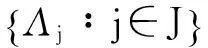
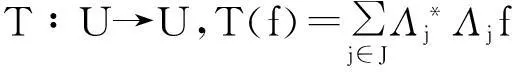
证明∀g∈U,有

因此,T是自伴算子.于是有

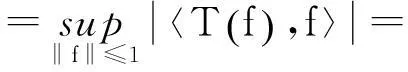
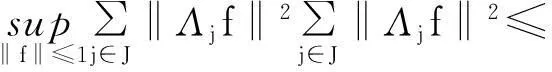
‖T‖‖f‖2,∀f∈U

(2)

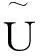
即对一切j∈J,有Λjf=0.因此,f=0.进一步,T在U上有闭值域,从而在闭子空间上的限制算子也有闭值域.于是我们有

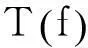
‖T‖‖f‖

再由Cauchy-Schwartz不等式和式(2)得

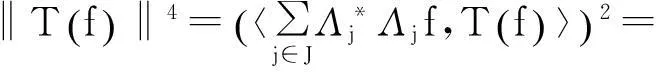
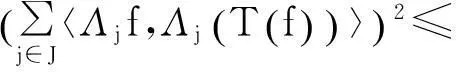
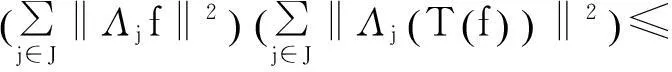
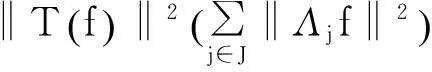
所以,

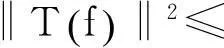
于是,

‖T‖-1‖T-1‖-2‖f‖2

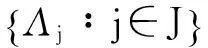
2单位分解与g-框架

本节我们主要讨论单位分解的一些简单性质及与g-框架的关系.

2.1　单位分解的概念和简单性质

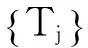
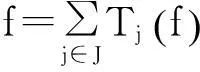
且序列无条件收敛.

我们知道,对于g-框架有重构公式

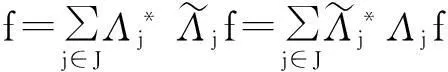
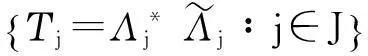
接下来我们介绍单位分解的一些性质.

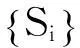
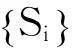
因此,

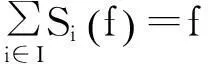
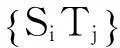
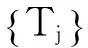
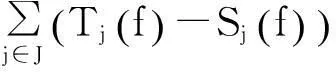
∀f∈U

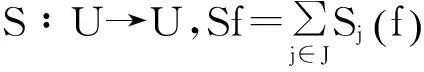
则

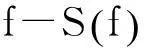
λ‖f‖

因此,‖Id-S‖≤λ<1,所以S可逆,且对∀f∈U,有

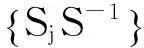
2.2　单位分解和g-框架

利用单位分解,我们又可以得到一种求g-框架下界的方法.

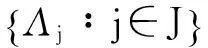
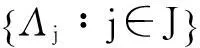
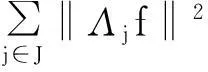
参考文献:

[1] Christensen O.An Introduction to Frames and Riesz Bases[M].Boston:Birkhauser，2003.

[2] Grochenig K.Foundations of Time-Frequency Analysis[M].Boston， Birkhauser，2001.

[3] Han D G, Larson D R.Larson,Frames,bases and group representations[J].Mem Amer Math Soc,2000,147(697)：1-94.

[4] 李登峰,薛明志.Banach空间上的基和框架[M].北京:科学出版社,2007.

[5] Fornasier M.Quasi-orthogonal decompositions of structured frames[J].J Math Anal Appl,2004,289(1):180-199.

[6] Casazza P G,Kutyniok G.Frames of subspaces[M]// Wavelets,Frames and Operator Theory. Contemporary Mathematics, 2004:87-113.

[7] Asgari M S,Khosravi A.Frames and bases of subspaces in Hilbert spaces[J].J Math Anal Appl,2005,308(2):541-553.

[8] Li S D,Ogawa H.Pseudoframes for subspaces with applications[J].J Fourier Anal Appl,2004,10(4):409-431.

[9] Christensen O.Eldar Y C.Oblique dual frames and shift-invariant spaces[J].Appl Comput Harmon Anal,2004,17(1):48-68.

[10] Eldar Y C.Sampling with arbitrary sampling and reconstruction spaces and oblique dual frame vectors[J].J Fourier Anal Appl,2003,9(1):77-96.

[12] Sun W C.G-frames and g-Riesz bases[J].J Math Anal Appl,2006,322(1):437-452.

[13] Sun W C.Stability of g-frames[J].J Math Anal Appl,2007,326(2):858-868.

(编辑：姚佳良)