旋转矢量法在振动与波中的应用

旋转矢量法在振动与波中的应用

柯 尧*

(江西省九江第一中学江西 九江332000)

摘 要：旋转矢量法是求解振动与波动问题的一种重要而又有效的方法，本文通过3个高考题介绍了旋转矢量法的应用，从而拓展了解决振动与波相关问题的解题思路.

关键词：旋转矢量法振动波动

收稿日期：(2014-10-24)

作者简介：*柯尧(1983-)，男，中教一级，主要从事高中物理教学及研究.一直担任物理竞赛教学、物理竞赛特级教练，曾辅导多名学生进入国家冬令营.

1何谓旋转矢量法

如图1，A为一长度保持不变的矢量，A的始点在x坐标轴原点处，计时起点t=0时，矢量与坐标轴夹角为α，矢量A以角速度ω0逆时针匀速转动，因此，矢量A在任一瞬间与x轴夹角为ω0t+α，用x表示矢量A在坐标轴上的投影，有x=Acos(ω0t+α).可见，匀速旋转矢量在坐标轴上的投影可表示一特定的简谐振动.不难发现旋转矢量的长度等于振幅；矢量A旋转的角速度等于简谐振动的角频率；矢量A与x轴正方向的夹角等于简谐振动的相位.通常将此方法称为旋转矢量法，又称为简谐振动的几何表示法[1].

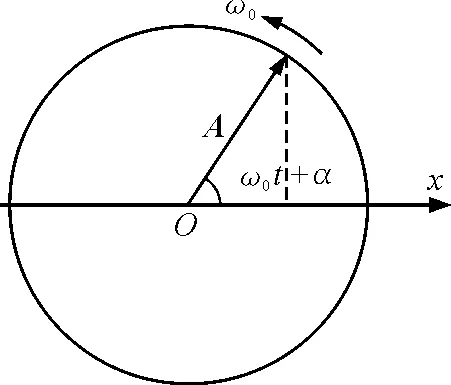
图1　旋转矢量法示意图

旋转矢量法将数学表达式转化成了动态的图形，相当于数学中的数形结合.美国数学家斯蒂恩曾说,“如果一个特定的问题可以转化为一个图形，那么思想就整体地把握了问题，并且能创造性地思索问题的解法”.本文通过举例说明旋转矢量法在解高考题中的应用.

2旋转矢量法在简谐振动中的应用

振动是自然界中一种非常常见的运动形式，几乎所有的微振动都可视为简谐振动.旋转矢量法可以十分直观地描述振动物体的位移、速度、加速度、相位等物理量的变化.特别是在处理同频率振动的合振动上更是体现其简便易行.

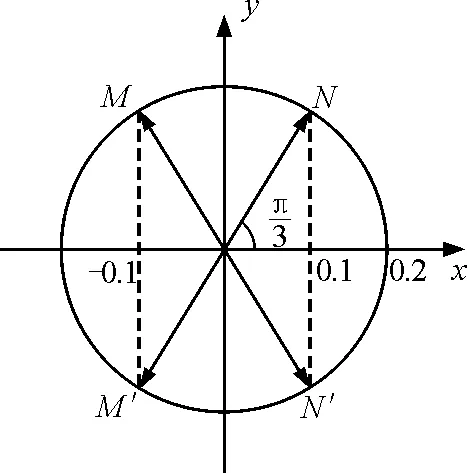
图2

或

或

即

或

或

其中k=0,1,2,…

或

或

即

或

或

其中k=0,1,2,…

3旋转矢量法在波动中的应用

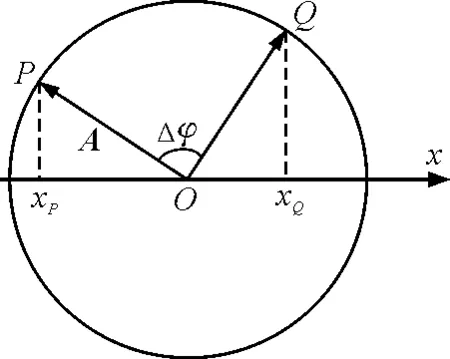
图3　 Q落后 P的相位

分析：解决波动的题常规方法是利用质点的振动情况画出波形图，再根据波形图判断质点的运动情况，但是本题质点所处的位置既不是最大位移也不是最小位移，通过画波形求出答案难度较大.不妨尝试通过旋转矢量法来分析.

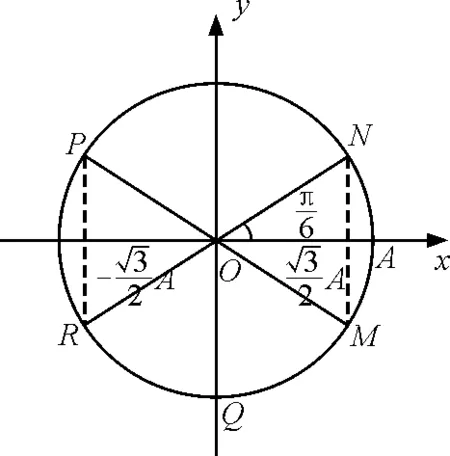
图4

A．上方且向上运动

B．上方且向下运动

C．下方且向上运动

D．下方且向下运动

图5

通过上述3例不难发现，旋转矢量法在解决振动或波动问题时，的确有独到之处.在高中阶段，振动一般不要求作复杂的定量计算.但在物理竞赛和自主招生试题中可能就会出现复杂的计算，这时旋转矢量法更是能体现其简便.旋转矢量法的应用远不止这些，其实凡是按正余弦变化的量都可以进行矢量化，都可以让问题在直观的图形中解决.

参 考 文 献

1漆安慎，杜婵英．力学．北京：高等教育出版社，1997.265