基础提离对核电站结构地震响应的影响分析

第一作者王国波男，博士，副研究员，硕士生导师，1979年生

基础提离对核电站结构地震响应的影响分析

王国波1，王亚西1,于艳丽2，何卫2

(1. 武汉理工大学道路桥梁与结构工程湖北省重点实验室,武汉430070；2. 武汉理工大学土木工程与建筑学院,武汉430070)

摘要：当地震足够大时结构基础将会与下卧地基土发生分离，即所谓的基础提离现象。但该现象在常规的土-结构相互用(SSI)的地震响应分析中常常被忽视。核电站结构(NPP)由于特殊性，其设计地震强度一般较大，因而有可能发生基础提离现象。基于某简化核电站结构，利用大型通用软件ANSYS的接触面功能和弹簧单元，分别进行了四种工况的计算：①基础固定；②考虑基础提离，不考虑土-结构动力相互作用效应；③不考虑基础提离，但考虑土-结构动力相互作用效应；④同时考虑基础分离和土-结构动力相互作用效应。通过对比分析，确定合适的土-结构动力相互作用计算方法以及基础提离对核电站结构地震响应的影响。计算分析表明：①土-结构相互作用对核电站结构地震响应的影响不容忽视；②基础提离主要影响核电站结构竖向地震响应，而对结构水平向地震响应的影响较小。本文研究成果可为核电站结构的抗震分析提供参考。

关键词：基础提离；土-结构相互作用；地震响应；接触面；核电站

基金项目：国家自然科学基金青年基金项目(51208406);教育部留学回国人员科研启动基金；中央高校基本科研业务费专项资金项目(2014-Ⅳ-088)

收稿日期：2013-11-01修改稿收到日期：2013-12-19

中图分类号:TU.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.036

Abstract:The structure foundation may be separated from the supporting soil if the earthquake is strong enough, which is the so called phenomenon of foundation uplift. This phenomenon, unfortunately, is always neglected in seismic response analysis of soil-structure interaction (SSI) system. The designed seismic level for nuclear power plant (NPP) is usually very high because of its specificity, therefore, the foundation of nuclear power plant will probably be separated from the supporting soil. Based on a simplified NPP calculation model and by employing the contact function and spring element in the software ANSYS, four cases were considered: ① foundation is fixed; ② foundation uplift is considered and SSI effect is not considered; ③ SSI effect is considered and foundation uplift is not considered; ④ both foundation uplift and SSI effect are considered. The influences of SSI and foundation uplift on structural seismic response were analyzed by comparing the computation results. It is shown from the computation results that the influence of SSI on structural seismic response can not be neglected; foundation uplift influences structural vertical response mainly, and has a very little influence on structural horizontal response. The results provide some references to seismic design of NPP.

Analysis on the influence of foundation uplift on structure seismic response

WANGGuo-bo1,WANGYa-xi1,YUYan-li2，HEWei2(1. Hubei Key Laboratory of Roadway Bridge & Structure Engineer; Wuhan University of Technology; Wuhan 430070, China；2. School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, China)

Key words:foundation uplift; soil-structure interaction; seismic response; contact interface; nuclear power plant

早期对于结构地震响应分析一般基于两方面的假设，一是将结构基础下的土体简化为理想的刚性体，即不考虑土-结构的动力相互作用效应(SSI)；二是认为结构基础与地基土是“绑定”在一起的，即不考虑结构基础提离的影响。对于前者，土-结构相互作用问题的重要性早已得到了人们的普遍认可和重视。但是大量的考虑SSI的研究工作仍基于第二个假设[1]，即没有考虑基础提离的影响。

结构基础与地基的部分分离现象，即基础提离现象在多次地震中均有观测，如在1952年美国加利福尼亚地震中，大量石油裂化塔发生了强烈的摇晃，并将其基础下的锚杆拉出；在1964年阿拉斯加地震中，在一些油库的基础下面发现有冰，从而间接证明了在地震时油库基础发生了提离现象[2]。如果基础提离量较大的话，结构就有可能发生倾覆，如在一些地震中观察到一些倾覆的纪念碑和墓碑，这也是结构基础与地基发生提离现象的有力证据。然而或许是在震后调查中难以发现小量的基础提离，目前针对建筑物基础提离的观测还不够丰富，但这并不意味着建筑物在地震中不会发生这种现象[2]。

由于上述一些间接证据的存在，20世纪70~80年代间大量学者对基础提离现象进行了理论分析，其中Housner[3]的研究工作被公认为是第一个明确地将基础提离与结构地震响应联系起来的学者。随后的研究中有代表性的分析模型主要有两种：一是Winkler地基模型，即将地基土模拟为连续分布的弹簧单元[4]；二是简化的两弹簧地基模型，即将地基土简化为置于基础两端的弹簧单元[5-6]。

俞载道等[7]进行该方面研究，详细探讨了土-单自由度结构相互作用体系的基础提离、滑移等现象对其地震响应的影响。到目前为止，国内在该领域的研究大多集中在油库、桥墩等结构基础提离的分析上，针对一般建筑物与核电站结构的研究还较少。

本文针对某简化核电站模型，对其进行三维的计算分析，确定基础提离对结构地震响应的影响，同时也分析土-结构动力相互作用对核电站结构地震响应的影响。

1简化核电站模型

该简化的核电站结构模型为对称结构(图1)，内部为五层结构(图2)，结构基础如图3所示，基础总面积为6 599.2 m2，底板厚3m，水平向宽100 m，每层层高10 m。在计算土体阻抗时，将该基础等效为圆形基础，平动和转动等效基础半径分别为45.8 m和46.3 m。整个核电站结构总重量为2.3×108kg。该模型共包括8 230个节点，其中结构基础含有949个节点，9 224个单元。其中结构全采用SHELL181单元模拟。

地基土参数为：剪切波速1 100 m/s，质量密度2 350 kg/m3，泊松比0.4。结构采用理想弹塑性模型，其计算参数为：弹性模量为36 GPa，密度2 500 kg/m3，泊松比0.2。

为尽可能考虑足够高频率的影响，本文计算的时步取为0.001 s。

对于阻尼的考虑，考虑两部分：一是土体的阻尼，通过土阻抗函数考虑(即在弹簧单元中输入实常数，具体见下节)；二是结构的阻尼，采用常用的瑞利阻尼模型，其中阻尼比取常用的经验值(0.05)。

图1 整体计算模型Fig.1Globalcomputationmodel图2 结构内部示意图Fig.2Structuredinternalschematicdiagram图3 结构基础Fig.3Structurefoundation

2计算工况及其实现方法

为充分说明土-结构动力相互作用及基础提离对核电站结构地震响应的影响，本文考虑四种工况：

(1)不考虑土-结构相互作用和基础提离。实现方法：完全固定结构的基础。

(2)考虑基础提离的影响，但不考虑土-结构相互作用。实现方法：由于不考虑土-结构的相互作用，因此，土体采用一刚性面代替，然后在这层刚性面与结构基础之间设置接触面单元。对于接触面单元，详细信息可参见ANSYS帮助文件，这里仅交代比较重要的两点：①接触算法选用罚函数法，该方法采用接触弹簧建立目标面和接触面之间的关系，默认的弹簧刚度值(接触刚度)由系统根据单元尺寸及刚度等因素确定，也可人为指定；②接触面模型选用粗糙型(rough)：为降低过多因素的影响，本文仅考虑基础提离的影响，而暂时忽略基础滑移的影响，因而选用粗糙接触面模型，该模型假定结构基础与土体之间的摩擦力无穷大。

(3)不考虑基础提离，但考虑土-结构动力相互作用。实现方法：将地基土简化为分布于结构基础底面的弹簧-阻尼器单元，利用ANSYS中的COMBIN14单元模拟。该弹簧单元既可模拟压缩，也可模拟拉伸，因此，采用该单元时，基础提离现象不会发生。弹簧常数(刚度和阻尼)则利用经典的阻抗函数经典公式确定，具体计算细节见下节。

(4)同时考虑基础提离和土-结构相互作用。实现方法：将地基土简化为分布于结构基础底面的弹簧-阻尼器单元，利用ANSYS中的COMBIN14和COMBIN39单元模拟。由于不考虑结构基础与土体之间的滑移，因此水平向弹簧仍采用COMBIN14单元，而竖向和转动方向则采用COMBIN39单元，参照文献[8]，通过设置COMBIN39单元的F-D曲线，使其只能提供压力，而不能提供拉力，以模拟在结构基础的提离现象，也即当弹簧单元出现拉力时，就表明此时基础与地基土发生了分离现象。典型的F-D曲线如图4所示，其中曲线的斜率即为阻抗函数计算的刚度值。其中第三象限的曲线模拟弹簧的压缩，第一象限的曲线模拟弹簧的受拉。理论而言，曲线在第一象限应为0，即不提供拉力。但本文中在第一象限提供了少量的拉力是出于两方面的原因：①是软件计算的需要，该单元要求第一象限内所定义的F-D曲线在原点处的斜率为正(大于零)；②实际工程结构的土-结构接触面处由于摩擦等作用，多少存在一定的附着力(attaching force)，因此，这里定义一个很小的位移值(detZ=4×10-7)，使在该处拉力最大，然后很快衰减为零。

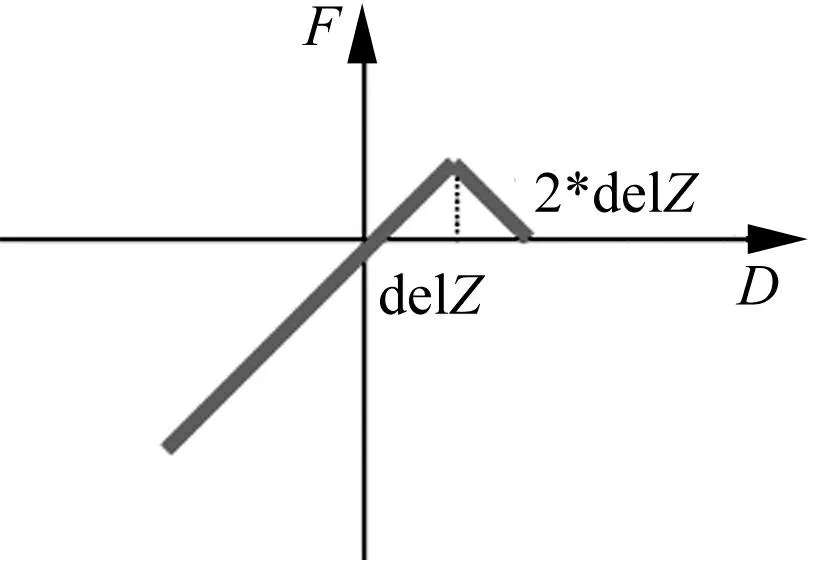
图4　COMBIN39单元的F-D曲线 Fig.4 F-D curve for COMBIN39 element

3阻抗函数的计算

目前已有大量成熟的经验公式计算地基土的阻抗函数，比较著名的有Richart公式[9]、Veletsos公式[10]以及Gazetas[11-12]总结适用于任意形状基础的公式等。本文采用美国核电站抗震规范推荐的经验公式[13](作者已经做过比较分析，不同经验公式得到的结果十分接近)，具体公式见表1所示。其中v、G、ρ分别为地基土的泊松比、剪切模量和质量密度，R为基础特征尺寸(如圆形基础的半径)，Ir和It分别为结构绕坐标轴的质量惯性矩和极转动惯量。表1中的数值为计算值，该计算值是作用于结构基础底面的总刚度值和阻尼值，在具体计算时，由于基础底板有949个节点，即有949个弹簧单元，上述总刚度值和阻尼值需根据每个节点所代表的面积与基础总面积的比值分配到各个弹簧单元。

表1　土体阻抗函数计算公式

需补充说明的是，上述公式均是假设基础为明置基础，既没有考虑基础的埋深。本文也按明置基础考虑，主要是基于如下两方面的原因：一是结构基础的埋深显然是有利于结构抗震；二是结构基础尺寸一般较大，埋置深度不大。因此，从有利于结构抗震以及简化分析的角度考虑，本文也按明置基础考虑。

4输入地震波

本文采用著名的El-Centro波作为输入地震波，加速度时程曲线如图5所示。

已有研究表明，在考虑基础提离现象时，在考虑水平向地震动输入的同时必须考虑竖向地震动的影响，因此，本文考虑水平横向(X向)和竖向(Z向)同时输入El波。

为使基础发生提离现象，所需地震需足够大，同时为放大基础提离的影响，本文考虑在水平向和竖向同输入地震波，水平向地震动幅值取3倍的El波(峰值为10.251 m/s2，1.05 g)，竖向地震动峰值则取水平向的2/3，即6.834 m/s2(0.7 g)。为节约时间，仅取前6.5 s进行计算。

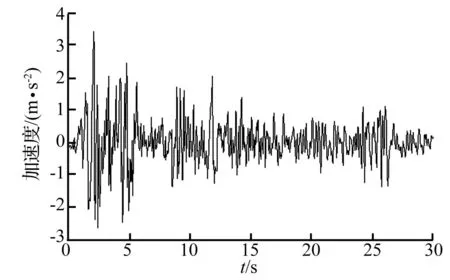
图5　输入地震波 (El波) Fig.5 Input seismic wave (El wave)

5计算结果及分析

为简化叙述，采用FIX代表工况1，Contact代表工况2，COM14代表工况3，COM39代表工况4。限于篇幅，本文仅给出结构基础节点4 636的竖向位移、结构顶层楼板正中间节点625的加速度和位移时程曲线。另外，由于楼板水平向加速度反应谱曲线对于核电站结构抗震分析较为重要，因此同时给出顶层楼板正中节点(节点625)水平加速度反应谱曲线(节点位置可参见图2和图3)。

5.1体系频率

先对体系进行模态分析，获取结构的前10阶自振频率，如表2所示。由表可见：

(1)考虑土-结构相互作用后，体系的基频显著降低(从5.956 5降到4.369 3)，表明土-结构相互作用对体系的刚度影响十分显著；

(2)对于工况2(接触单元)，虽没有考虑土-结构的相互作用，但采用的接触算法为罚函数法，其本质仍是在结构基础与刚性板之间设置接触弹簧，只不过该接触弹簧的接触刚度非常大，因此，此时结构的频率稍有降低，但其影响可忽略不计；

(3)工况3和工况4两种情形下的结构频率完全相同，这是合理的。因为二者的区别仅在于是否允许地基发生提离现象，在模态分析阶段，两种弹簧单元的作用其实是相同的，因此，两情形下体系频率完全一致。

表2　四种工况下体系的前10阶自振频率

5.2基础分离面积

工况2和工况4考虑了基础的提离，可按如下方法确定最大的基础分离面积：

(1)对于工况2：先确定基础角点节点4 636的竖向最大位移所对应的时间(荷载步)，获取该荷载步时的计算结果，然后获取结构基础节点的接触状态(状态值为3表示仍接触，状态值小于3表示分离，其中又分为近区域分离、远区域分离等，具体可参见ANSYS帮助文件)，从而确定已分离的节点，如图6所示(图中显示的节点即为分离的节点)。

(2)对于工况4：同样地，先确定基础角点节点4 636竖向最大位移所对应的时间(荷载步)，获取该荷载步时的计算结果，此时竖向位移大于图4中给定detZ值的节点便已分离，如图7所示(图中显示的节点即为分离的节点)。

图6　工况2时基础的分离节点 Fig.6 The separated nodes on the foundation for case 2

图7　工况4时基础的分离节点 Fig.7 The separated nodes onthe foundation for case 4

对比图6、7可见：图6对应的工况2由于没有考虑土-结构的相互作用，导致体系刚度较大，地震响应也较大，因而分离面积较大，基础提离比达到了50%左右，而图7对应的工况4则考虑了土-结构的相互作用，因而基础提离面积较小，基础提离比达仅30%左右。再次可见土-结构动力相互作用对该核电站结构地震响应的影响不容忽视。

5.3基础节点的竖向位移

图8为四种工况时基础节点4 636点的竖向位移时程曲线(由于工况1时基础固定，因此这里仅给出了后三种工况的结果)。由图可见：工况2由于只考虑了基础提离，未考虑土-结构相互作用，因而体系刚度大，结构地震响应也大，基础角点的竖向位移最大，最大值约4 cm，其次是工况4，最后是工况3(仅考虑土-结构相互作用)。由此可见：基础提离对结构竖向响应较为显著。

图8 节点4636的竖向位移时程曲线Fig.8Verticaltimehistorycurvesatnode4636图9 节点625的水平位移时程曲线Fig.9Horizontaldisplacementtimehistorycurvesatnode625图10 节点625的竖向位移时程曲线Fig.10Verticaldisplacementtimehistorycurvesatnode625

图11 节点625的水平加速度时程曲线Fig.11Horizontalaccelerationtimehistorycurvesatnode625图12 节点625的竖向加速度时程曲线Fig.12Verticalaccelerationtimehistorycurvesatnode625图13 节点625的水平加速度反应谱曲线Fig.13Horizontalaccelerationresponsespectracurvesatnode625

5.4核电站结构的响应

限于篇幅，本文仅给出最高层楼板正中间节点(编号625，参见图2)的位移(图9为水平，图10为竖向)及加速度(图11为水平，图12为竖向)时程曲线，以及水平向加速度反应谱曲线(图13)。为了使图形清晰、可读，工况1的曲线没有给出。

对比分析上述图9-13可有：

(1)对比图9、11结构水平响应的工况3和工况4可见：仅在2-2.5s基础发生最大分离时基础提离对结构水平响应有较小的影响，在其余时间段，两情况下结构的水平响应十分接近，由此可见基础提离对结构水平向响应的影响较小；

(2)对比图10、12的结构竖向响应可见：以同时考虑基础提离和土-结构动力相互作用的工况4的情形最大，其次是考虑基础提离的工况2，仅考虑土-结构相互作用的工况3最小。这表明对于结构的竖向响应，基础提离的影响不容忽视；

(3)对比图13结构水平加速度反应谱曲线可见：首先，体系的卓越频率在工况1(固定情形)时最大，工况2时居中，工况3、4(考虑土-结构相互作用)时最小，这与前面模态分析结果相吻合，同时也体现了土-结构动力相互作用对结构动力特性的影响；其次，从反应谱曲线峰值来看，工况1时最大，其次是工况2，工况3、4的最小。

6讨论与结论

6.1讨论

基于上述详细的计算分析，作者拟对如下三个问题进行讨论。

6.1.1土-结构相互作用是否考虑的合理标准

在很多国家(如中国、韩国等)的核电站抗震规范中，规定当地基土剪切波速达到或高于1 100 m/s时，可不考虑土-结构动力相互作用，即可按基础固定的情形进行结构抗震分析和设计。本文在计算时也特意选择剪切波速为1 100 m/s，但从计算结果及上述分析来看，此时土-结构动力相互作用的影响仍不容忽视。由此可见，这种仅规定地基土刚度的方法并不十分合理。

美国标准ASCE 4-98[13]则建议采用地基土与结构的刚度比作为是否考虑土-结构动力相互作用的标准，该标准可用下式表示：

fFIX≤1.12fSSI

即当基础固定时体系的基频(fFIX)小于等于1.12倍的考虑土-结构相互作用时体系的基频(fSSI)，此时才可以不考虑土-结构相互作用的影响。

本文中fFIX和fSSI分别为5.956 5 Hz和4.369 3 Hz，此时fFIX> 1.12fSSI，不满足上式的条件，因此，土-结构动力相互作用的影响必须考虑，这与本文的分析相吻合。

6.1.2体系非线性的考虑

基础提离是在较大地震情形下才会发生，因此，基础提离同时包含了几何非线性和材料非线性，是一个十分复杂的现象。在本文的计算中，作者仅利用理想的弹塑性本构模型考虑了上部结构材料的非线性，而对于几何非线性(基础提离)还停留在弹性分析，这是不尽合理之处。实际上，随着基础与地基土发生分离，分离基础所对应的弹簧单元将失去功效，剩下发生功效的弹簧单元刚度系数和阻尼系数均将随着发生变化，这是一个渐进的过程，理论上可通过逐步迭代的方法实现。文献[14]针对二维情形给出了迭代算法，但对于基础是一条线的二维模型，分离点容易确定，因而迭代算法也容易实现。本文是三维模型，基础是一个面，这个迭代算法的实现还面临一些困难，作者也正在努力实现中。尽管如此，作者仍然认为该弹性范围内的近似计算分析结果仍具有一定的参考价值，同时，作者在此也将本文计算所存在的问题提出，期望能起到抛砖引玉的作用。

6.1.3基础提离和滑移的同时考虑

实际工程中基础发生提离时，基础或多或少的会发生一定的水平向滑移。但本文为了简化影响因素，突出分析并确定基础提离对核电站结构地震响应的影响，因而未在文中同时考虑基础水平滑移的影响，这也是后续进一步计算分析需完善之处。

6.2结论

本文基于某简化核电站模型，进行了多个工况的详细计算，分析了土-结构动力相互作用及基础提离对核电站结构地震响应的影响。基于计算分析，可得如下主要结论：

(1)对于该核电站结构而言，土-结构动力相互作用的影响十分明显，其效应不容忽视；

(2)基础提离主要影响结构的竖向响应，而对结构水平向响应的影响较小，主要体现在基础发生显著分离的时间段；

(3)目前一些国家的核电站结构抗震规范中关于土-结构动力相互作用是否考虑的规定不尽合理，因为该规定仅考虑了地基土的刚性。

致谢:本文研究工作是作者在阿海珐集团(AREVA Group)从事博士后科研工作期间完成的，具体计算工作得到了阿海珐集团同事MOUSSALLAM Nadim、石家庄铁道学院王新敏老师以及中国石油大学(华东)张如林博士的大力帮助，同时该课题研究也获得了国家自然科学基金青年基金(编号：51208406)的资助，在此一并表示感谢！

参考文献

[1]Chopra A K, Yim C S. Simplified earthquake analysis of structures with foundation uplift[J]. Journal of Structural Engineering, 1985, 111(4): 906-930.

[2]Psycharis I N, Jennings P C. Rocking of slender rigid bodies allowed to uplift[J]. Earthquake Engineering and Structural Dynamic, 1982, 11(1): 57-76.

[3]Housner G W. The behavior of inverted pendulum structures during earthquake[J].Bulletin of the Seismological Society of America, 1963, 53(2): 403-447.

[4]Yim C S, Chopra A K. Earthquake response of structures with partial uplift on Winkler foundation[J]. Earthquake Engineering and Structural Dynamic, 1984, 12(2): 263-281.

[5]Yim C S, Chopra A K. Dynamics of structures on two-spring foundation allowed to uplift[J]. Journal of Engineering Mechanics, 1984, 110(7): 1124-1146.

[6]Song Y H, Lee D G. An improved two-spring model for foundation uplift analysis[J]. Computers and Structures, 1993, 46(5):791-805.

[7]俞载道，职洪涛，曹国敖. 基础提离、滑移对结构地震反应影响的探讨[J]. 同济大学学报(自然科学版), 1997, 25(2): 141-146.

YU Zai-dao, ZHI Hong-tao, CAO Guo-ao. Study on the effect of base uplifting and sliding on earthquake response of structures[J]. Journal of Tongji University(Natural Science Edition), 1997, 25(2): 141-146.

[8]Naohiro N, Susumu I, Osamu K, et al. An estimation method for basemat uplift behavior of NPP buildings[C]. 18th International Conference on Structural Mechanics in Reactor Technology (SMiRT18), Beijing, 1995.

[9]Richart F E, Hall J R, Woods R D. Vibrations of soils and foundations[M]. Englewood cliffs, New Jersey, Prentice Hall Inc. 1970.

[10]Veletsos A S, Verbic B. Vibration of viscoelastic foundations[J]. Earthquake Engineering and Structure Dynamics, 1973, 2: 87-102.

[11]Dobry R,Gazetas G. Dynamic response of arbitrary shaped foundations[J]. Journal of Geotechnical Engineering, 1984, 112(2): 109-135.

[12]Gazetas G. Formulas and charts for impedances of surface and embedded foundations[J]. Journal of Geotechnical Engineering, 1991, 117(9): 1363-1381.

[13]ASCE Standard 4-98, Seismic analysis of safety-related nuclear structures and commentary[S]. ASCE, 1999.

[14]Sung G C, Yong I L, Jae S K, et al. A study on the criterion of fixed base condition in soil-structure interaction analysis of nuclear power plant structure[C]. 18th International Conference on Structural Mechanics in Reactor Technology (SMiRT18), Toronto, 2007.