黏弹性地基中基于虚土桩模型的桩顶纵向振动阻抗研究
2016-01-07吴文兵,蒋国盛,邓国栋等
第一作者吴文兵男,博士,副教授,1988年生
黏弹性地基中基于虚土桩模型的桩顶纵向振动阻抗研究
吴文兵1,蒋国盛1,邓国栋2,谢邦华1
(1.中国地质大学(武汉)工程学院,武汉430074;2.中南大学土木工程学院,长沙410075)
摘要:基于虚土桩模型,对均质黏弹性地基中桩土纵向耦合振动问题进行了研究。首先,假定桩侧土为各向同性的线性黏弹性材料,并考虑土体的竖向波动效应,结合Euler-Bernoulli杆件理论,建立了桩土纵向耦合振动的定解问题;其次,采用分离变量法求解桩侧土纵向振动的控制方程,得到了桩侧土与桩身接触面上的剪切动刚度,将所得的剪切动刚度代入到桩身振动控制方程,采用Laplace变换技术,进一步求得了任意荷载作用下桩顶纵向振动阻抗的解析解。基于所得解,详细讨论了不同桩身设计参数时桩端土厚度对桩顶纵向振动阻抗的影响。最后,将虚土桩模型与其他桩端土支承模型进行了对比研究,结果表明,对虚土桩模型选用合适的材料参数和桩端土厚度,其得到的桩端支承复刚度值介于现有多种模型的计算值之间。
关键词:虚土桩模型;纵向振动阻抗;黏弹性地基;竖向波动效应;Laplace变换;解析解
基金项目:国家自然科学基金青年项目(51309207);中国博士后科学基金特别资助项目(2013T60759);中国博士后科学基金面上项目(2012M521495);中央高校基本科研业务贵专项资金-摇篮计划(CUGL150411)
收稿日期:2013-10-21修改稿收到日期:2014-04-16
中图分类号:TU435
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.07.030
Abstract:Based on fictitious soil pile model, the vertical dynamic response of pile embedded in homogeneous viscoelastic soil was investigated. Assuming the surrounding soil of pile to be isotropic viscoelastic material and considering its vertical wave effect, the definite problem of soil-pile system subjected to arbitrary dynamic force was established based on the Euler-Bernoulli rod theory. The shear dynamic stiffness at the interface of soil and pile was derived by means of separation of variables to solve the governing equation of surrounding soil. Substituting the shear dynamic stiffness acquired into the governing equation of pile, the analytical solution of vertical dynamic impedance was deduced by virtue of Laplace transform technique. Based on the obtained solution, the influence of depth of pile end soil on the vertical dynamic impedance was studied in detail with different design parameters of pile. Constrast analysis was made between the fictitious soil pile model and other pile end soil supporting models. It is shown that the complex supporting stiffness calculated by fictitious soil pile model is in the middle of the supporting stiffnesses calculated by other existing models if adopting appropriate material parameters and proper depth of pile end soil in the fictitious soil pile model.
Vertical dynamic impedance of pile embedded in viscoelastic soil based on fictitious soil pile model
WUWen-bing1,JIANGGuo-sheng1,DENGGuo-dong2,XIEBang-hua1(1. Engineering Faculty, China University of Geosciences, Wuhan, Hubei 430074, China; 2. School of Civil Engineering, Central South University, Changsha, Hunan 410075, China)
Key words:fictitious soil pile model;vertical dynamic impedance;viscoelastic soil;vertical wave effect;Laplace transform;analytical solution
桩与土体的动力相互作用问题包括两个方面,一是桩与桩侧土的动力相互作用,二是桩与桩端土的动力相互作用。现有成果关于桩与桩侧土动力相互作用模型的研究已经比较丰富,如动态Winkler模型[1-6]、平面应变模型[7-12]、三维连续介质模型[13-17]。相比之下,由于对桩与桩端土动力相互作用建立严格耦合模型的难度较大,现有成果关于该课题的研究显得比较薄弱。现有桩与桩端土的动力相互作用模型归纳起来有刚性支承模型[3,10,17]和黏弹性支承模型[4-6, 11, 16, 18-21]两大类。刚性支承模型人为的将桩端土当作刚性边界,这对端承桩具有足够的精度,但对摩擦桩却存在明显的不足。对于摩擦型桩只能采用黏弹性支承模型,然而大部分的黏弹性性支承模型都将土体假设为半无限空间体,如模拟公式法[18]、常数取值法[19]、Q-z曲线方程式法[20]及极限承载力理论法[21]等,与土体的实际情况存在差异,而且支承参数大多根据经验取得,严格耦合的情况较少。因此,为了更加合理地模拟桩与桩端土的动力相互作用,笔者及合作者们提出了虚土桩模型[22-23]。虚土桩模型的主要思想是把桩端正下方至基岩之间的圆柱形土体看成“土桩”,将桩端土对桩的支承作用转化为“土桩”与桩之间的相互作用问题。吴文兵等[24]利用虚土桩模型求解了半空间地基上刚性圆板的垂直振动问题,并将虚土桩模型解与现有精确解得到的结果进行对比分析,验证了虚土桩模型具有比较高的精度。虚土桩模型能够充分考虑桩端以下土体的成层性及材料性质等因素,可以避免假设桩端支承,对于摩擦型桩的研究不再限制于半无限空间的假定,又可退化为桩底端承的状态,因此该模型具有减少假设条件,与实际场地相吻合的先进性,是一个较为严格的理论模型。
基于虚土桩模型,本文在考虑土体竖向波动效应的条件下,结合Laplace变换技术,推导得到了任意荷载作用下均质黏弹性地基中桩顶纵向振动阻抗的解析解,并详细讨论了桩端土参数对桩顶纵向振动阻抗的影响。在本文工作的基础上可以进一步研究复杂工况下桩基的纵向振动问题,这对桩基振动理论应用于桩基动力设计有着重要的理论意义。
1数学模型
1.1计算模型
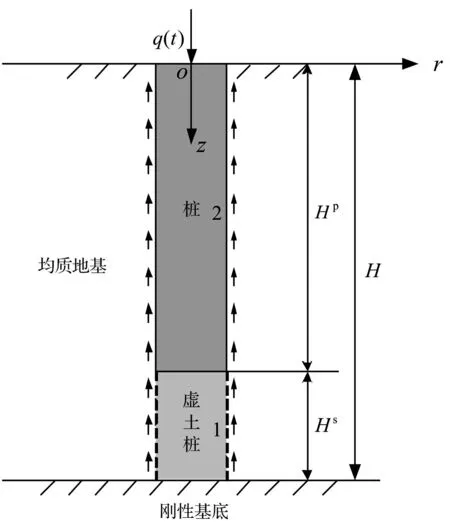
图1 计算模型 Fig.1 Calculating model
桩土系统动力相互作用的计算简图如图1所示,桩长为Hp,桩身截面半径为r0,桩顶作用有任意激振力q(t),桩侧土层厚度为H,其中桩端土厚度(虚土桩长度)为Hs。根据桩、虚土桩桩身材料性质的差异,以桩端为界将虚土桩与桩分别编号为1、2。
1.2假设条件
假设下列条件成立:
(1)桩侧土为均质、各向同性的线性黏弹性材料,土体材料阻尼为粘性阻尼,阻尼力与应变率成正比,比例系数为ηs;
(2)土层上表面为自由边界,无正应力、剪应力,土层底部为刚性支承边界;
(3)桩土系统纵向振动时,考虑桩侧土竖向波动效应,桩侧土径向位移可忽略;
(4)桩及虚土桩均为完全弹性、竖直、圆形均匀截面桩,桩与虚土桩交界面处应力应变连续;
(5)桩土系统振动为小变形振动,桩(虚土桩)与桩侧土完全连续接触。
2定解问题的建立
取土体中任意一点的纵向振动位移为w=w(r,z,t),根据黏弹性动力学理论,考虑土体纵向位移,建立轴对称黏弹性土体动力平衡方程如下:
(1)
式中,λs、Gs为土体Lame常数,且有λs=Esμs/[(1+μs)(1-2μs)],Gs=ρs(Vs)2,Es为土体的弹性模量,μs为土体的泊松比,Vs为土体的剪切波速,ηs为土体的粘性阻尼系数,ρs为土体的密度。
(2)
令uj=uj(z,t)为桩(虚土桩)身质点纵向振动位移,根据Euler-Bernoulli杆件理论,可得桩(虚土桩)作纵向振动的控制方程如下:
(j=1,2)
(3)
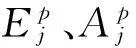
结合假设条件,建立桩土系统边界条件和初始条件如下:
(1)土层的边界条件
土层顶面:
(4a)
土层底面:
(4b)
水平无穷远处:
σ(∞,z)=0、w(∞,z)=0
(4c)
(2)桩顶、虚土桩底及桩与虚土桩分界处的边界条件
(5a)
(5b)
(5c)
(5d)
(3)桩土接触面上的边界条件
w(r0,z,t)=uj(z,t)(j=1,2)
(6)
(4)桩土系统的初始条件
土层部分:
(7a)
桩(虚土桩)身部分:
(7b)
3定解问题的求解
3.1土层振动问题求解
令W(r,z,s)为w(r,z,t)的Laplace变换形式,结合初始条件(7a),对土层动力平衡方程(1)进行Laplace变换并化简可得:
(8)

由于式(8)左边的第一项和第二项分别为关于纵向和径向的微分式,因此可将其分离为两个常微分方程:
(9)
(10)
式中,β和ξ为常数,且满足如下关系式:
(11)
方程(9)、(10)分别为一个Bessel方程和二阶常微分方程,可分别得到相应通解,然后利用分离变量法性质可进一步得到土体位移W(r,z,s)的表达式如下:
W(r,z,s)=[AK0(ξr)+BI0(ξr)]·
[Csin(βz)+Dcos(βz)]
(12)
式中,I0(·)、K0(·)分别为零阶第一类、第二类虚宗量Bessel函数,A、B、C和D是由边界条件确定的待定系数。
由虚宗量Bessel函数的性质可知:r→∞时,In(·)→∞,Kn(·)→0,结合边界条件(4c)可以得到:B=0。由边界条件(4a)可以得到:C=0。对边界条件(4b)进行Laplace变换,并将式(12)代入可得:
cos(βH)=0
(13)
(14)
式中,An为一系列由边界条件决定的待定系数,反映桩土振动各模态的振动耦合作用。ξn是当β=βn时可由式(11)确定的一系列参数。
3.2桩振动问题求解
令U(z,s)为u(z,t)的Laplace变换形式,对式(3)进行Laplace变换,并结合式(2)和(14),将式(3)化简可得:
(j=1,2)
(15)
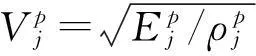

(16)
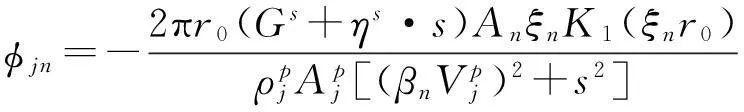
根据虚土桩法的基本思想,先求得虚土桩顶的阻抗函数,然后将其作为桩的桩端支承刚度代入到桩中进行分析,因此,接下来分为两步求解:
第一步:求解虚土桩桩顶位移阻抗函数
对边界条件(6)进行Laplace变换,并将式(14)和式(16)代入,同时,根据固有函数系cos(βnz)在[0,Hs]上的正交性,在变形后的边界条件(6)两边乘以cos(βkz)并在桩端土厚度范围[0,Hs]内积分可得:
(17)
将式(17)代入式(16)可得虚土桩的位移幅值表达式如下:
(18)
式中,
χ″1n=
(20)
(21)
(22)
(23)
对边界条件(5b)进行Laplace变换,并将式(18)代入Laplace变换后的边界条件可得:
(24)
由位移阻抗函数的定义可得虚土桩桩顶的复阻抗函数为:
(25)
第二步:求解桩顶位移阻抗函数值。
类似第一步的求解方法,可得下式:
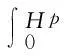
(26)
将式(26)代入式(16)可得桩顶的位移幅值表达式如下:
(27)
式中,

χ″2n=
(29)
(30)
φ2n=K0(ξnr0)+
(31)
(32)
将虚土桩桩顶阻抗函数(25)作为桩端的支承刚度代入到桩的方程,由边界条件(5c)、(5d)可得:
(33)
由位移阻抗函数的定义可得桩顶的复阻抗函数为:
(34)
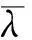
Z2(s)=K+iC
(35)
4分析计算与讨论
基于桩顶复阻抗的解析解,本节将详细讨论不同桩身设计参数时桩端土厚度对桩顶纵向振动阻抗的影响,其中均质地基土的计算参数如无特别说明,均取为:密度为1 800 kg/m3,剪切波速为180 m/s,泊松比为0.4,粘性阻尼系数为1 000 N·m-3·s。
4.1不同桩长时桩端土厚度对桩顶复阻抗的影响
桩长是影响桩基础承载力的重要参数之一,且现有研究表明,桩长也是影响桩土振动特性的主要参数。因此,首先讨论不同桩长时桩端土厚度对桩顶动力响应的影响。用于计算的桩身参数为:桩长分别为10 m和20 m,截面半径为0.5 m,密度为2 500 kg/m3,弹性纵波波速为3 800 m/s。定义桩身截面直径为d,桩端土厚度分别为:Hs=0.5d,1d,3d,5d。


图2 不同桩长时桩端土厚度对桩顶复阻抗的影响Fig.2Influenceofdepthofpileendsoiloncompleximpedanceatpilehead图3 不同桩径时桩端土厚度对桩顶复阻抗的影响Fig.3Influenceofdepthofpileendsoiloncompleximpedanceatpilehead图4 不同桩身混凝土等级时桩端土厚度对桩顶复阻抗的影响Fig.4Influenceofdepthofpileendsoiloncompleximpedanceatpilehead
图2反映了在桩基础动力设计关注的低频范围内,不同桩长时桩端土厚度对桩顶复阻抗的影响。由图2(a)可以看出,动刚度随着频率的增大呈增大趋势。在同一频率处,动刚度随着桩端土厚度的增大而逐渐减小,但当桩端土厚度大于一定值之后,动刚度将不再受桩端土厚度增大的影响。由图2(b)可以看出,当频率超过5Hz以后,动阻尼随着频率的增大基本呈现线性增大的趋势。随着桩端土厚度的增大,同一频率处的动阻尼也逐渐增大,但当桩端土厚度大于一定值之后,动阻尼将不再受桩端土厚度增大的影响。由图2还可以看出,当桩越长,动刚度和动阻尼随着桩端土厚度变化的幅度越小。
4.2不同桩径时桩端土厚度对桩顶复阻抗的影响
讨论不同桩径时桩端土厚度对桩顶复阻抗的影响时,用于计算的桩身参数为:桩长为15 m,截面半径分别为0.3 m和0.5 m,密度为2 500 kg/m3,弹性纵波波速为3 800 m/s。桩端土厚度分别为:Hs=0.5d,1d,3d,5d。
图3反映了在桩基础动力设计关注的低频范围内,不同桩径时桩端土厚度对桩顶复阻抗的影响。由图可以看出,桩径较小时,随着桩端土厚度的增大,动刚度逐渐减小,动阻尼逐渐增大,但两者的变化幅度均较小,且当桩端土厚度增大到一定值之后,动刚度和动阻尼将不再受到桩端土厚度继续增大的影响。当桩径较大时,动刚度和动阻尼随着桩端土厚度增大的变化规律与桩径较小时一致,但变化幅度要比桩径较小时的变化幅度大。
4.3不同桩身混凝度等级时桩端土厚度对桩顶复阻抗的影响
讨论不同桩身混凝土等级时桩端土厚度对桩顶复阻抗的影响时,根据单因素分析原则,可通过变化桩身混凝土纵波波速来反映其等级的变化。用于计算的桩身参数为:桩长为15m,截面半径为0.5 m,密度为2 500 kg/m3,弹性纵波波速分别为3 600 m/s和4 000 m/s。桩端土厚度分别为:Hs=0.5d,1d,3d,5d。
图4反映了在桩基础动力设计关注的低频范围内,不同桩身混凝土等级时桩端土厚度对桩顶复阻抗的影响。由图可以看出,随着桩端土厚度的增大,动刚度逐渐减小,动阻尼逐渐增大,且当桩端土厚度增大到一定值之后,动刚度和动阻尼曲线将趋于一致。由图还可以看出,桩身混凝土等级对动刚度和动阻尼随桩端土厚度的变化幅度基本没有影响。
5不同桩端支承模型的对比研究
目前已有的桩基振动理论研究中,不管是桩端刚性支承,还是桩端黏弹性支承,均可以用桩端土支承复刚度来表示,写成如下形式:
Zb=kb+ηb·iω
(36)
式中,kb为桩端支承刚度系数,ηb为桩端支承阻尼系数,可以通过调整kb和ηb来反映桩端土对桩的支承情况。接下来,将虚土桩模型与现有桩端支承模型进行对比分析,计算参数为:桩长为15 m,截面半径为0.5 m,密度为2 500 kg/m3,弹性纵波波速为3 800 m/s,桩端土厚度分别为Hs=0.01d,0.1d,0.5d,2d。图中kb、ηb值的大小表示了其他桩端土支承模型,kb=∞,ηb=∞时为固定支承,kb=0,ηb=0时为自由支承,kb=15,ηb=15时为黏弹性支承。
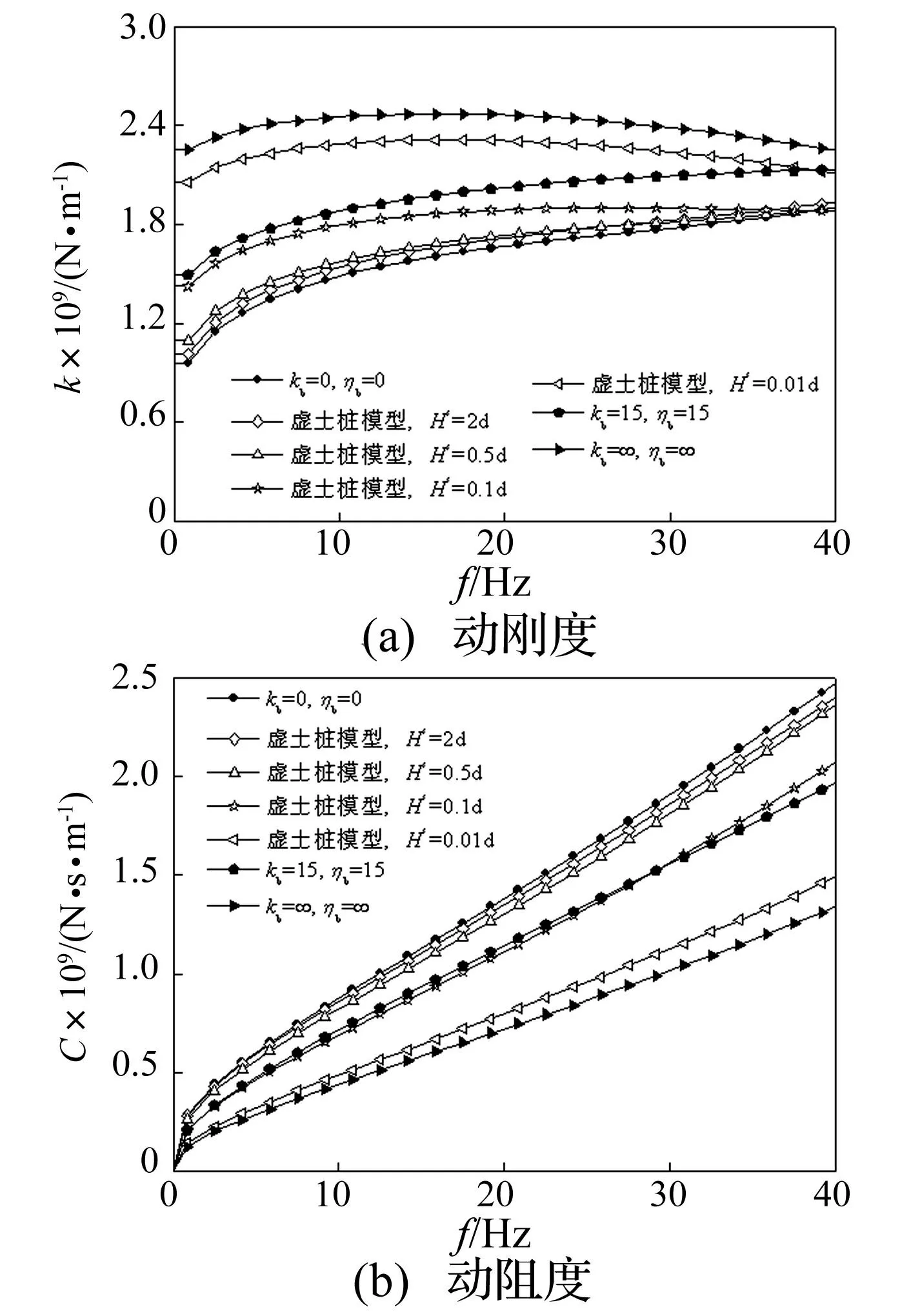
图5 桩端土支承模型对桩顶复阻抗的影响 Fig.5 Influence of bearing stiffness on complex impedance at pile head
图5反映了在桩基础动力设计关注的低频范围内,桩端土支承模型对桩顶复阻抗的影响。由图可以看出,由黏弹性桩端支承模型和虚土桩模型得到的动刚度和动阻尼介于桩端自由和桩端固定支承模型所得值之间,且当桩端土厚度从小到大逐渐变化时,所得到动刚度和动阻尼逐渐从桩端固定支承状态过渡到桩端自由支承状态。因此,针对桩端土质条件,对虚土桩模型选用合适的材料参数和桩端土厚度,其得到的桩端支承刚度值介于现有多种模型的计算值之间。但虚土桩模型能考虑桩端土的成层性及施工扰动效应,且虚土桩模型的参数直接可取桩端土的材料参数,而不必通过经验公式计算,能更加准确的反映桩端土对桩的支承作用,因此理论上更加严密。
6结论
本文通过综合分析桩端土厚度对桩顶复阻抗的影响,在桩基础动力设计关注的低频范围内得到如下结论:
(1)随着桩端土厚度的增大,同一频率处的动刚度逐渐减小,同一频率处的动阻尼则逐渐增大。但当桩端土厚度增大到一定值之后,桩端土厚度的继续增大将不会对动刚度和动阻尼产生影响。这说明,桩身动力响应只能影响到有限厚度的桩端土层,当桩端土层厚度超过一定值之后将不再受到桩身动力响应的影响,即桩端土对桩身动力响应的影响存在一个临界影响厚度,在临界影响厚度范围内,桩端土厚度的变化将会对桩身动力响应产生很大影响。
(2)当桩越长或桩径越小时,动刚度和动阻尼随着桩端土厚度变化的幅度越小,反之则越大。桩身混凝土等级对动刚度和动阻尼随着桩端土厚度变化的幅度基本没有影响。
(3)通过将虚土桩模型与现有其他理论模型对比发现,针对相应桩端土质条件,对虚土桩模型选用合适的材料参数,其得到的桩端支承刚度值介于现有多种模型的计算值之间。但虚土桩模型能考虑桩端土的成层性及施工扰动效应,且虚土桩模型的参数直接可取桩端土的材料参数,而不必通过经验公式计算,能更加准确地反映桩端土对桩的支承作用,因此理论上更加严密。因此,虚土桩模型能够较真实地反映桩与桩端土相互作用机理,是一个比较严格的理论分析模型。
参考文献
[1]Novak M,Beredugo Y O. Vertical vibration of embedded footings[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1972, 98(12): 1291-1310.
[2]Nogami T,Konagai K. Time domain axial response of dynamically loaded single piles[J]. Journal of Engineering Mechanics, ASCE, 1986, 112(11): 1241-1252.
[3]王奎华,谢康和,曾国熙. 有限长桩受迫振动问题解析解及其应用[J]. 岩土工程学报, 1997, 19(6):27-35.
WANG Kui-hua, XIE Kang-he, ZENG Guo-xi. Analytical solution to vibration of finite length pile under exciting force and its application[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(6):27-35.
[4]孔德森, 栾茂田, 杨庆. 桩土相互作用分析中的动力Winkler模型研究评述[J]. 世界地震工程, 2005, 21(1): 12-17.
KONG De-sen, LUAN Mao-tian, YANG Qing. Review of dynamic Winkler model appfied in pile-soil interaction analyses[J]. World Earthquake Engineering, 2005, 21(1):12-17.
[5]刘东甲. 指数型变截面桩中的纵波[J]. 岩土工程学报, 2008, 30(7):1066-1071.
LIU Dong-jia. Longitudinal waves in piles with exponentially varying cross sections[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(7):1066-1071.
[6]Wang K H, Wu W B, Zhang Z Q, et al. Vertical dynamic response of an inhomogeneous viscoelastic pile[J]. Computers and Geotechnics, 2010, 37(4): 536-544.
[7]Nogami T, Novak M. Soil-pile interaction in vertical vibration[J]. Earthquake Engineering and Structural Dynamics, 1976,4(3):277-293.
[8]Veletsos A S, Dotsos K W. Vertical and torsional vibration of foundations in inhomogeneous media[J]. Journal of Geotechnical Engineering, ASCE, 1988, 114(9): 1002-1021.
[9]Militano G, Rajapakse R K N D. Dynamic response of a pile in a multi-layered soil to transient torsional and axial loading[J]. Geotechnique, 1999, 49(1): 91-109.
[10]王海东, 尚守平. 瑞利波作用下径向非匀质地基中的单桩竖向响应研究[J]. 振动工程学报, 2006, 19(2): 258-264.
WANG Hai-dong, SHANG Shou-ping. Research on vertical dynamic response of single-pile in radially inhomogeneous soil during passage of Rayleigh waves[J].Journal of Vibration Engineering, 2006, 19(2): 258-264.
[11]王奎华,杨冬英,张智卿. 基于复刚度传递多圈层平面应变模型的桩动力响应研究[J]. 岩石力学与工程学报,2008,27(4):825-831.
WANG Kui-hua,YANG Dong-ying,ZHANG Zhi-qing. Study on dynamic response of pile based on complex stiffness transfer model of radial multizone plane strain[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4):825-831.
[12]吴文兵,王奎华,窦斌. 任意层地基中黏弹性楔形桩纵向振动响应研究[J].振动与冲击, 2013, 32(8): 120-127.
WU Wen-bing, WANG Kui-hua, DOU Bin. Vertical dynamic response of a viscoelastic tapered pile embedded in layered foundation[J].Journal of Vibration and Shock, 2013, 32(8): 120-127.
[13]Rajapakse R K N D, Chen Y, Senjuntichai T. Electroelastic field of apiezoelectric annular finite cylinder[J]. International Journal of Solids and Structures, 2005, 42(11-12): 3487-3508.
[14]Senjuntichai T, Mani S, Rajapakse R K N D. Vertical vibration of an embedded rigid foundation in a poroelastic soil[J]. Soil Dynamics and Earthquake Engineering, 2006, 26(6-7): 626-636.
[15]Wang K H, Zhang Z Q, Chin J L, et al. Dynamic torsional response of an end bearing pile in transversely isotropic saturated soil[J]. Journal of Sound and Vibration, 2009, 327(3): 440-453.
[16]胡昌斌, 黄晓明. 成层黏弹性土中桩土耦合纵向振动时域响应研究[J]. 地震工程与工程振动, 2006,26(4):205-211.
HU Chang-bin, HUANG Xiao-ming. A quasi-analytical solution to soil-pile interaction in longitudinal vibration in layered soils considering vertical wave effect on soils[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(4):205-211.
[17]刘林超, 闫启方, 杨骁. 分数导数黏弹性土层模型中桩基竖向振动特性研究[J]. 工程力学, 2011, 28(8): 177-182.
LIU Lin-chao, YAN Qi-fang, YANG Xiao. Vertical vibration of single pile in soil described by fractional derivative viscoelastic model[J]. Engineering Mechanics, 2011, 28(8): 177-182.
[18]Lysmer J, Richart F E. Dynamic response of footing to vertical loading[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1966, 2(1):65-91.
[19]Novak M, Beredugo Y O. Vertical vibration of embedded footings[J]. Journal of the Soil Mechanics and Foundation Division, ASCE. 1972, 98(12):1291-1310.
[20]Liang R Y, Husein A I. Simplified dynamic method for pile-driving control[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1993, 119(4):694-713.
[21]Meyerholf G G. Bearing capacity and settlement of pile foundations[J]. Journal of Geotechnical Engineering Division, ASCE, 1976, 102(3):195-228.
[22]杨冬英,王奎华. 非均质土中基于虚土桩法的桩基纵向振动[J]. 浙江大学学报(工学版), 2010, 44(10): 2021-2028.
YANG Dong-ying, WANG Kui-hua.Vertical vibration of pile based on fictitious soil-pile model in inhomogeneous soil[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(10): 2021-2028.
[23]吴文兵,王奎华,杨冬英,等. 成层中基于虚土桩模型的桩基纵向振动响应[J]. 中国公路学报, 2012, 25(2): 72-80.
WU Wen-bing, WANG Kui-hua, YANG Dong-ying, et al. Longitudinal dynamic response to the pile embedded in layered soil based on fictitious soil pile model[J]. China Journal of Highway and Transport, 2012, 25(2): 72-80.
[24]吴文兵,王奎华,张智卿,等. 半空间地基中虚土桩模型的精度分析及应用[J]. 应用基础与工程科学学报, 2012, 20(1): 121-129.
WU Wen-bing, WANG Kui-hua,ZHANG Zhi-qing, et al. Accuracy and application of virtual soil pile model in half space foundation[J]. Journal of Basic Science and Engineering, 2012, 20(1): 121-129.


